if (2x,3y) =(8, 9),find x and y
Answers

Answer:
Step-by-step explanation:
2x=8 and 3y=9
x=8/2 and y=9/3
x=4 and y=3
Related Questions
Xifeng has $30 to spend at a craft fair. She returns home with $0 and some very nice crafts. What integer represents the change in the amount of money Xifeng has?
Answers
Answer:
-30
Step-by-step explanation:
Integers by definition are whole numbers (positive & negative), and includes the number zero.
In this case, Xifeng spent $30, meaning that she "lose $30" or -30.
~
Explain how to identify a starting position on a line.

Answers
Answer:
it depends on the type of line but for a straight line the starting point is always the edge that is A
Solve each equation.
1/4 x²+ 7/2x=-12
Answers
The solutions to the equation 1/4 x² + 7/2x = -12 are x = -6 and x = -8.
To solve the equation 1/4 x² + 7/2x = -12, we can start by multiplying the entire equation by 4 to eliminate the fraction:
4 * (1/4 x² + 7/2x) = 4 * (-12)
This simplifies to:
x² + 14x = -48
Now, rearrange the equation in standard form:
x² + 14x + 48 = 0
To solve this quadratic equation, we can factor it or use the quadratic formula. In this case, let's factor it:
(x + 6)(x + 8) = 0
Setting each factor equal to zero, we get:
x + 6 = 0 or x + 8 = 0
Solving for x in each equation:
x = -6 or x = -8
Thus ,the solutions to the equation 1/4 x² + 7/2x = -12 are x = -6 and x = -8.
To know more about quadratic equation, click here
https://brainly.com/question/30098550
#SPJ11
3/14
turned into a decimal
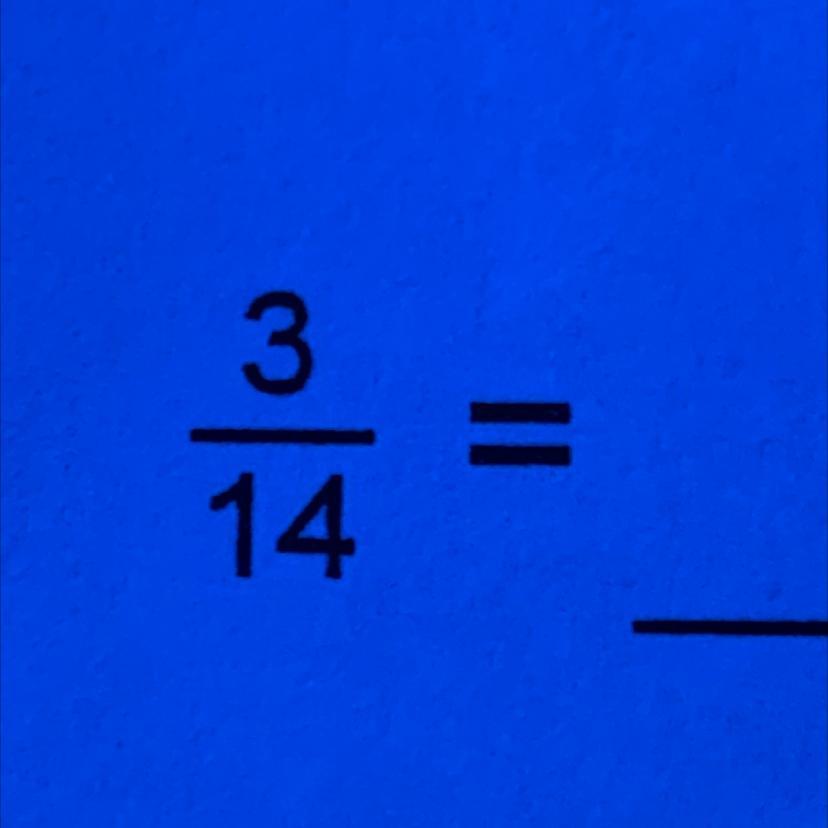
Answers
Answer:
i believe it is 0.2143
Step-by-step explanation:
Answer:
0.21428571428
Step-by-step explanation:
I hope this help.
-16 -12 -8 -4
Common difference of the arithmetic sequence
Answers
What is a counterexample for the conjecture? if the perimeter of a rectangle is 40 units, the area must be at least 1 square unit.
Answers
The counterexample is if the length of the rectangle is 19.99 and width is 0.01 then the area is 0.1999 and the perimeter still 40.
What is Counterexample?Counterexample are those examples which is used to make given statement false , Or its an instance of example.
Given ,
The perimeter of the rectangle = 40 units
It is mentioned in the statement that if perimeter is 40 then area must be at least 1 unit .
The counterexample for proven this statement false would be ,
The rectangle whose length is 19.99 unit and width is 0.01 unit have the area 0.1999 square unit and perimeter is 40 unit .
Hence , It is proved by counterexample that it is not necessary that area must be at least 1 unit when perimeter is 40 unit .
Learn more about Counterexample:
brainly.com/question/24881803
#SPJ1
8(3x-4)=15x+40
24x-32=15x+40
?
9x=72
x=8
What’s the next step after 24x-32=15x+40
Answers
Find the volume of the solid generated by revolving the region in the first quadrant bounded by the coordinate axes, the curve y=e^x, and the line x=ln8 about the line x = ln 8
a. Volume = 2π(1 - ln 8)
b. Volume = 2π(1 + ln 8)
c. Volume = 2π(7 - ln 8)
c. Volume = 2π(7+ ln 8)
Answers
The solid formed by rotating the specified area around the line x = ln 8 has a volume of 2(7 + ln 8). This is obtained by calculating the area of the region and multiplying it by the distance between the line x = ln 8 and the axis of revolution.
The volume of a solid generated by revolving a two-dimensional region about an axis is equal to the area of the region multiplied by the distance between the axis of revolution and the region. The region given to us is bounded by the coordinate axes, the curve y =\(e^x\), and the line x = ln 8. We can calculate the area of this region by using the method of integration. We need to take the integral of the function y = \(e^x\) from the lower bound x = ln 8 to the upper bound x = 1. This will give us the area of the region. Then, we multiply this area by the distance between the line x = ln 8 and the axis of revolution. This distance is equal to 7 + ln 8, and thus the volume of the solid generated is equal to 2π(7 + ln 8).
Learn more about volume here
https://brainly.com/question/16134180
#SPJ4
Echinacea is widely used as an herbal remedy for common cold, but does it work? In a double-blind experiment, healthy volunteers agreed to be exposed to common-cold- causing rhinovirus type 39 and have their symptoms monitored. The volunteers were randomly assigned to take either a placebo of an Echinacea supplement for 5 days following viral exposure. Among the 103 subjects taking a placebo, 88 developed a cold, whereas 44 of 48 subjects taking Echinacea developed a cold. (use plus 4 method) Give a 95% confidence interval for the difference in proportion of individuals developing a cold after viral exposure between the Echinacea and the placebo. State your conclusion.
Answers
Using the plus 4 method, the 95% confidence interval for the difference in proportion of individuals developing a cold after viral exposure between the Echinacea and the placebo is (-0.158, 0.397). Based on this confidence interval, we can conclude that there is no significant difference in the proportion of individuals developing a cold between the Echinacea and the placebo groups.
To determine the 95% confidence interval for the difference in the proportion of individuals developing a cold between the Echinacea and placebo groups, we can use the plus 4 method for small sample sizes.
First, we calculate the proportions of individuals who developed a cold in each group.
In the placebo group, out of 103 subjects, 88 developed a cold, giving a proportion of 88/103 ≈ 0.854.
In the Echinacea group, out of 48 subjects, 44 developed a cold, giving a
proportion of 44/48 ≈ 0.91
Next, we add 2 to the number of successes and 2 to the total number of observations in each group to apply the plus 4 adjustment.
This gives us 90 successes out of 107 observations in the placebo group (0.841) and 46 successes out of 52 observations in the Echinacea group (0.885).
To calculate the 95% confidence interval, we can use the formula:
\(CI = (p1 - p2) \pm Z \times \sqrt{(p1(1-p1)/n1} + p2(1-p2)/n2)\)
where p1 and p2 are the adjusted proportions, n1 and n2 are the respective sample sizes, and Z is the critical value for a 95% confidence interval (approximately 1.96).
Substituting the values into the formula, we get:
\(CI = (0.841 - 0.885) \pm 1.96 \times \sqrt{((0.841(1-0.841)/107) + (0.885(1-0.885)/52))}\)
Calculating the values within the square root and the overall expression, we can find the lower and upper bounds of the confidence interval.
Interpreting the results, if we repeat this experiment many times and construct 95% confidence intervals, we can expect that approximately 95% of these intervals will contain the true difference in proportions
In this case, if the interval contains 0, it suggests that there is no significant difference between Echinacea and placebo in terms of the proportion of individuals developing a cold after viral exposure. However, if the interval does not include 0, it indicates a significant difference, suggesting that Echinacea may have an effect on reducing the likelihood of developing a cold.
For similar question on confidence interval.
https://brainly.com/question/20309162
#SPJ8
solve sinx = 2x-3 using false position method
Answers
The root of the equation sinx = 2x-3 is 0.8401 (approx).
Given equation is sinx = 2x-3
We need to solve this equation using false position method.
False position method is also known as the regula falsi method.
It is an iterative method used to solve nonlinear equations.
The method is based on the intermediate value theorem.
False position method is a modified version of the bisection method.
The following steps are followed to solve the given equation using the false position method:
1. We will take the end points of the interval a and b in such a way that f(a) and f(b) have opposite signs.
Here, f(x) = sinx - 2x + 3.
2. Calculate the value of c using the following formula: c = [(a*f(b)) - (b*f(a))] / (f(b) - f(a))
3. Evaluate the function at point c and find the sign of f(c).
4. If f(c) is positive, then the root lies between a and c. So, we replace b with c. If f(c) is negative, then the root lies between c and b. So, we replace a with c.
5. Repeat the steps 2 to 4 until we obtain the required accuracy.
Let's solve the given equation using the false position method.
We will take a = 0 and b = 1 because f(0) = 3 and f(1) = -0.1585 have opposite signs.
So, the root lies between 0 and 1.
The calculation is shown in the attached image below.
Therefore, the root of the equation sinx = 2x-3 is 0.8401 (approx).
Learn more about equation
brainly.com/question/29657983
#SPJ11
The size of a large milkshake is 1. 4 times the size of a small milkshake. Write a percent that compares the size of the large milkshake to the size of the small milkshake.
Answers
The percentage comparing the size of the large milkshake to the size of the small milkshake is 140%.
Let the size of small milkshake he x. So, the size of large milkshake will be 1.4x. Now, for percentage calculation the formula will be -
Percentage = size of large milkshake/size of small milkshake × 100
As we need to find the percentage of ratio, we need to simply take large and small size of milkshake.
Keep the values in formula -
Percentage = 1.4x/x ×100
Cancelling x from numerator and denominator
Percentage = 1.4 ×100
Performing multiplication
Percentage = 140%
Hence, the percentage is 140%.
Learn more about percentage -
https://brainly.com/question/24877689
#SPJ4
please help with this question I really need quick geometry

Answers
7) The transformation is a dilation by a scale factor of 1.5.
8) The transformation here is; Rotation 180° about the origin.
How to carry out transformations?
7) We are told that ABCG is transformed to KHIJ.
Coordinates of ABCG are;
A(-2, -3), B(0, 5), C(6, 0), G(1, -3)
Now, coordinates of KHIJ are;
K(-3, -4.5), H(0, 7.5), I(9, 0), J(1.5, -4.5)
Now, from the transformed shape, we see that its' coordinates are 1.5 times that of the original shape coordinates. Thus, we can say that the transformation is a dilation by a scale factor of 1.5.
8) We are told that ABC is transformed to KLJ.
Coordinates of ABC are;
A(-9, 8), B(-4, 7), C(-7, 1)
Now, coordinates of KLJ are;
K(9, -8), L(4, -7), J(7, -1)
It is clear that the transformation here is;
(x, y) → (-x, -y)
From transformation rules, we can say that the transformation here is;
Rotation 180° about the origin.
Read more about Transformations at; https://brainly.com/question/4289712
#SPJ1
Charge Q
1. =6.0nC is at (0.30 m,0), charge Q
2 =−1.0nC is at (0,0.10 m), and charge Q
3 =5.0nC is at (0,0). What is the magnitude of the net electrostatic force on the 5.0−nC charge due to the other charges? (k=8.99×10^9 N⋅m^2C ^2 )
Answers
The magnitude of the net electrostatic force on the 5.0−nC charge due to the other charges when the charge Q1 = 6.0 nC is at (0.30 m, 0), charge Q2 = −1.0 nC is at (0, 0.10 m), and charge Q3 = 5.0 nC is at (0, 0) is 6.21 N.
The value of the net electrostatic force on the 5.0-nC
charge due to the other charges when the charge Q1 = 6.0 nC is at (0.30 m, 0),
charge Q2 = −1.0 nC is at (0, 0.10 m), and
charge Q3 = 5.0 nC is at (0, 0) can be calculated as follows:
Given data,Charge Q1 = 6.0 nC is at (0.30 m, 0),
Charge Q2 = -1.0 nC is at (0, 0.10 m),
Charge Q3 = 5.0 nC is at (0, 0)
The formula to find out the force on the third charge Q3 is:
F = k * |Q1 * Q3| / r1^2 + k * |Q2 * Q3| / r2^2
Here, k = 8.99 × 10^9 N·m^2/C^2, Q1 = 6.0 nC, Q2 = -1.0 nC, Q3 = 5.0 nC
For the third charge Q3, the distance from Q1 is:
r1 = √(0.3^2 + 0^2) = 0.3 m
And the distance from Q2 is: r2 = √(0^2 + 0.1^2) = 0.1 m
Substituting all the given values in the formula:
F = 8.99 × 10^9 * [ (6.0 × 10^-9 * 5.0 × 10^-9) / 0.3^2 ] + 8.99 × 10^9 * [ (-1.0 × 10^-9 * 5.0 × 10^-9) / 0.1^2 ]F = 6.21 N
Therefore, the magnitude of the net electrostatic force on the 5.0−nC charge due to the other charges when the charge Q1 = 6.0 nC is at (0.30 m, 0), charge Q2 = −1.0 nC is at (0, 0.10 m), and charge Q3 = 5.0 nC is at (0, 0) is 6.21 N.
Learn more about net electrostatic force
brainly.com/question/30076646
#SPJ11
Find the surface area and width of a rectangular prism with height of 6 cm, length of 5 cm, and the
volume of 240 cm³.
Answers
Answer:
236 cm^2 and 8 cm
Step-by-step explanation:
width=w
240=6(5)(w)
w=8 cm
area=2[(6)(5)+(6)(8)+(5)(8)]
area=236 cm^2
The value of a share of AT&T stock on that day wa \$97 50 more than the value a share of IBM HockUnx to represent the unknown value Write an algebraic expression for each of the quantities being compared 0 = the value of a share of AT&T Mock E = the value of a share of IBM stock
Answers
Answer:
\(A = 97.50 + H\)
Step-by-step explanation:
Given
Stocks: AT&T and IBM HockUnx
Required
Determine the algebraic expression
Represent AT&T with A and IBM HockUnx with H.
Since AT&T is 97.5 more than IBM HockUnx;
The required expression is:
\(A = 97.50 + H\)
I need help plsssss I suck at math show, tell me why and show your work.

Answers
Answer:
The correct equation to use would be : 4(2+5)
(Whether you use the distributive property or not you will get the same answer in this equation)
with the equation 4 × 2 + 5 Mihini would end up multiplying 4 × 2 which is not what she wants. (She wants to find the number that is 4 TIMES the SUM of 2 + 5
The inductive step of an inductive proof shows that for k ≥ 4 , if 2 k ≥ 3 k , then 2 k + 1 ≥ 3 ( k + 1 ) . In which step of the proof is the inductive hypothesis used? 2 k + 1 ≥ 2 ⋅ 2 k (Step 1)
≥ 2 ⋅ 3 k (Step 2)
≥ 3 k + 3 k (Step 3)
≥ 3 k + 3 (Step 4)
≥ 3 ( k + 1 ) (Step 5)
a. Step 1
b. Step 2
c. Step 3
d. Step 4
Answers
The proof progresses from step (c) to (d), (e), and finally concludes with (e), showing that 2^k+1 ≥ 3^(k+1). Therefore, step (c) is where the inductive hypothesis is used in this particular proof.
The inductive hypothesis is used in step (c) of the proof, which states that 2^k ≥ 3^k.
In an inductive proof, the goal is to prove a statement for all positive integers, typically starting from a base case and then applying the inductive step. The inductive hypothesis assumes that the statement is true for some value, usually denoted as k. Then, the inductive step shows that if the statement holds for k, it also holds for k + 1.
In this case, the inductive hypothesis assumes that 2^k ≥ 3^k is true. In step (c), the proof requires showing that if 2^k ≥ 3^k holds, then 2^(k+1) ≥ 3^(k+1). This step relies on the inductive hypothesis because it assumes the truth of 2^k ≥ 3^k in order to establish the inequality for the next term.
By using the inductive hypothesis, the proof progresses from step (c) to (d), (e), and finally concludes with (e), showing that 2^k+1 ≥ 3^(k+1). Therefore, step (c) is where the inductive hypothesis is used in this particular proof.
Learn more about inductive hypothesis
https://brainly.com/question/29525504
#SPJ11
can someone help me please im very confused and please use step by step please
-2/3x+1<7
Answers
Answer:
x>-9
Step-by-step explanation:p
1.) Subtract 1 from both sides
-2/3x+1<7
-1<-1
= -2/3x < 6
2.) Multiple the 3 (denominator) in order to get rid of the fraction
3(-2/3x) < (6)3
= -6/3x < 18 (simplify the 6/3 into 2)
= -2x < 18
3.) Divide by -2 (when you divide with a negative number, your sin is going to switch, meaning it will turn into a '>' sign)
-2x / -2 < 18/-2
= x > -9
*ALSO*
If you want to graph it on a number line, it would look something like the picture above. (the circle is open because it doesn't have the line underneath. You're symbol also indicates which way you shade!! < = left .....> = right.....think of them like arrows :) )

7. Simplify: -12(44 - 2)
A. 489 + 24
b. 482 - 24
C 484 - 24
d. 489 + 24
E. 169 -14
Answers

Give the corresponding snapshots of memory after each of the following set of statements has been executed.1.int x1;x1=3+4int x(1),z(5);x=__z=__z=z/++x;Now z=__
Answers
These are the corresponding snapshots of memory after each set of statements have been executed.The value of x becomes 2 and the value of z becomes 2.
To answer this question, we need to understand how memory works in a computer. Whenever we declare a variable, it is assigned a memory location, and whenever we assign a value to it, that value is stored in that memory location. The corresponding snapshot of memory is the state of memory after each set of statements has been executed.
So, let's look at the given statements and their corresponding snapshots of memory:
1. int x1; x1 = 3+4
In this statement, we are declaring a variable x1 of type integer and assigning it the value 3+4, which is 7. Therefore, the corresponding snapshot of memory would look like this:
| Variable | Memory Location | Value |
|----------|----------------|-------|
| x1 | 1000 | 7 |
2. int x(1), z(5); x = __z = __z = z/++x;
In this statement, we are declaring two variables x and z of type integer and assigning the value 1 to x and 5 to z. Then, we are dividing z by the pre-incremented value of x and assigning the result to both x and z.
The pre-increment operator increases the value of x by 1 before it is used in the division. Therefore, the value of x becomes 2 and the value of z becomes 2.
So, the corresponding snapshot of memory would look like this:
| Variable | Memory Location | Value |
|----------|----------------|-------|
| x1 | 1000 | 7 |
| x | 1004 | 2 |
| z | 1008 | 2 |
In summary, the corresponding snapshots of memory after executing the given set of statements are:
1. x1 = 7
| Variable | Memory Location | Value |
|----------|----------------|-------|
| x1 | 1000 | 7 |
2. x = 2, z = 2
| Variable | Memory Location | Value |
|----------|----------------|-------|
| x1 | 1000 | 7 |
| x | 1004 | 2 |
| z | 1008 | 2 |
Therefore, these are the corresponding snapshots of memory after each set of statements have been executed.
To know more about corresponding visit :
https://brainly.com/question/29207897
#SPJ11
if the product of 2 identical numbers is 324,find one of the number
Answers
let each of the numbers be x :
\(x \times x = 324\)\( {x}^{2} = 324\)\(x = \sqrt{324} \)\(x = 18\)Find an answer to match the equation:8p+5=-6p+1A.3B.-10C.60D.4E.20F.38G.-2/7H.-10.4I.0
Answers
The first thing we need to do is collect like terms; move all the terms in p to one side of the equation and move the rest to the other side of the equation;
\(\begin{gathered} 8p+6p=1-5 \\ 14p=-4 \end{gathered}\)We'll now divide both sides of the equation by 14, which will give us the below;
\(\begin{gathered} \frac{14p}{14}=\frac{-4}{14} \\ \\ p=\frac{-2}{7} \end{gathered}\)Therefore, the correct answer is option G which is -2/7 as seen in our answer.
The time series graph shows information about the percentages of people in a town that used the coffee shop for the years between 1980 and 2010.

Answers
Answer:
1. Increased
2. 70%
Step-by-step explanation:
The trend show that the percentage of the people in the town (Using coffee shop) increased during the period.
Prediction will be 70% users
What's 5.152 rounded to the nearest tenth
Answers
Answer:
It would be 5.2
Step-by-step explanation:
You round it to 5.2
Hope this helps!
Box 2:
length • width • height = (4x-1)•x•x^3
volume = 4x^5-x^4
Degree of length:
Degree of width:
Degree of height:
Degree of volume:
Answers
Degree of length=1
Degree of width=1
Degree of height=3
Degree of volume=5
The [SUM] of the degree of each factor is the degree of the product
Why does this make sense Answer is C
Since a linear function has a degree of 1, hence the degree of the length, width and height is 1. The degree of the volume is 3
Degree of a polynomialThe degree of an equation is the power of the leading variable.
Given the following measures
length = 4x - 1
width = x
height = x -3
Since a linear function has a degree of 1, hence the degree of the length, width and height is 1. The degree of the volume is 3
Learn more on degree of a function here: https://brainly.com/question/1600696
#SPJ6
What is the annual rate of interest if P400 is earned in three months on an investment of P20,000?
Answers
The annual rate of interest is 8%.
What is the annual rate?
Interest is the amount that is paid to an investor for the use of their funds. The interest that is paid is a function of amount invested, interest rate and the duration of the loan.
Interest = amount invested x interest rate x time
Annual rate = interest ÷ (amount invested x time)
= 400 ÷ (20,000 x 3/12) = 0.08 = 8%
To learn more about interest rate, please check: https://brainly.com/question/14935026
#SPJ4
What is the first step to isolate the variable term on one side of the equation?
2/3x=-1/2x+5
Answers
The first step to isolate the variable term on one side of the equation is to move all constant terms to the other side by adding or subtracting the appropriate terms.
To isolate the variable term on one side of the equation, the first step is to gather all terms containing the variable on one side and move all constant terms to the other side.
In the given equation:
2/3x = -1/2x + 5
We have variable terms on both sides: 2/3x and -1/2x. To isolate the variable term, we can start by moving the -1/2x term to the left side by adding 1/2x to both sides of the equation.
Adding 1/2x to both sides:
(2/3x) + (1/2x) = (-1/2x) + (1/2x) + 5
Simplifying the left side:
(2/3x + 1/2x) = 5
To combine the fractions, we need a common denominator. The common denominator of 3 and 2 is 6, so we can rewrite the left side:
(4/6x + 3/6x) = 5
Combining like terms on the left side:
(7/6x) = 5
Now, the variable term 7/6x is isolated on one side of the equation. To completely isolate the variable, we can multiply both sides of the equation by the reciprocal of the coefficient of x, which in this case is 6/7.
Multiplying both sides by 6/7:
(6/7) * (7/6x) = (5) * (6/7)
Simplifying:
1x = 30/7
The variable x is now isolated on the left side, and the equation simplifies to:
x = 30/7
Moving all constant terms to the opposite side of the equation by appropriately adding or deleting terms is the first step towards isolating the variable term on one side of the equation.
for such more question on variable
https://brainly.com/question/18042457
#SPJ8
The strength, S, of a wooden beam depends on the width and depth of the rectangular cross-section of the beam, but not on the length of the beam. For a particular type of wood, the value of S of a beam is proportional to the product of the width and the square of the depth of its cross-section. Suppose the strength of an oak beam is 69 , when the beam is 7 inches wide and 3 inches deep. Determine the strength, S, of the largest rectangular beam that can be cut from a 28 -inch-diameter oak tree, given that the beam must be 14 inches wide. Remember y is proportional to x if there is a constant k such that y=kx. The constant k is known as the constant of proportionality. a) S=9016 b) S=2231 c) S=8232 d) S=392
Answers
The real root of the equation is x = 40 - 39√2, which gives a value of S = 2231 approximately.
Given,The strength, S, of a wooden beam depends on the width and depth of the rectangular cross-section of the beam, but not on the length of the beam.
For a particular type of wood, the value of S of a beam is proportional to the product of the width and the square of the depth of its cross-section.
The strength of an oak beam is 69, when the beam is 7 inches wide and 3 inches deep.Thus, we can conclude that k, a constant of proportionality exists, such that: S=k(W x D²), where W is the width, D is the depth of the rectangular cross-section and S is the strength of the beam.
Let's use this to calculate k: When the beam is 7 inches wide and 3 inches deep, S=69. Thus, we get:k = S/W x D²=69/(7 x 3²)=1.
Thus, the equation for S becomes:S = W x D²The radius of the oak tree is 28/2 = 14 inches and the beam must be 14 inches wide.
This implies that the rectangular cross-section of the beam must be square (or the largest rectangular cross-section is a square). Let the side of the square cross-section be x.
Thus, we can write:S = x²Diameter, d = 28 inches => radius, r = 14 inchesWe need to determine the depth of the beam. The depth of the beam is half the height of the cylindrical log from which the beam is cut. The cylindrical log has a diameter of 28 inches. The beam has a width of 14 inches.
The largest rectangular cross-section is a square with sides of length x. This cross-section can be obtained by cutting the log at a height of x/2 from its center.Since the diameter is 28 inches, the radius is 14 inches. The height at which the beam is cut is h = 14 - x/2.
Thus, the depth of the rectangular beam cut from the cylindrical log is given by: D = 2(h) = 2(14 - x/2) = 28 - x.Using the relationship S = W x D² with S = 69, W = 14 and k = 1, we can write:x² (28 - x)² = 69Simplifying the above equation,x⁴ - 56x³ + 784x² - 69 = 0.
Using polynomial long division, we get:(x² + 16x - 69)(x² - 40x + 1) = 0The real root of the equation is x = 40 - 39√2, which gives a value of S = 2231 approximately.Therefore, the answer is (b) S = 2231.
The strength, S, of a wooden beam depends on the width and depth of the rectangular cross-section of the beam, but not on the length of the beam. Let the side of the square cross-section be x. Thus, we can write:S = x²Diameter, d = 28 inches => radius, r = 14 inches. Using the relationship S = W x D² with S = 69, W = 14 and k = 1, we can write:x² (28 - x)² = 69.The real root of the equation is x = 40 - 39√2, which gives a value of S = 2231 approximately.
To know more about real root visit:
brainly.com/question/21664715
#SPJ11
Please help me with this question, and show working.

Answers
Step-by-step explanation:
You substitute the given values into the formula
E = (1+0.12)^ 15-1 / 15
Put this one your calculator and round the answer to 2 d.p.
SOMEONE HELP ME PLS
Solve for x.

Answers
Answer:
X equals 6°.
Step-by-step explanation:
There is a geometry rule that states the outer angle of a triangle's interior angle is equivalent to the sum of the remaining two interior angles of the triangle. Following this rule, you can get that (6x + 8) + (5x + 8) = 82° ⇒ 11x + 16 = 82° ⇒ 11x = 66° ⇒ x = 6°.