Identify the center and radius of the circle with the following equation:
〖(x+3)〗^2+〖(y-1)〗^2=81

Answers
Answer:
centre (3 ,-1) , r=9
Explanation:
The standard form of the equation of a circle is.
∣
∣
∣
∣
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
a
a
(
x
−
a
)
2
+
(
y
−
b
)
2
=
r
2
a
a
∣
∣
−−−−−−−−−−−−−−−−−−−−−−−−−
where (a,b) are the coordinates of the center and r , the radius.
For the given equation: a = 3 , b = -1 and r = 9
hence centre = (3 ,-1) and radius = 9
Step-by-step explanation:
Related Questions
How do you show that f and G are inverses of each other?
Answers
First make the graph of the functions, then if the two graphs are symmetric with respect to the line y = x (mirror images over y = x ), then they are inverse functions.
Symmetric
A figure or shape that can be divided into two equal parts by a line is called symmetric figures.
Inverse Functions
The inverse function of a function f is a function that undoes the operation of f. The inverse of f exists if and only if f is bijective, and if it exists, is denoted by F^-1.
Learn more about graph and functions here :-
brainly.com/question/17267403
#SPJ4
Can somebody plz answer this correctly!!! tell me which I should circle?
(Grade5math)
(WILL MARK AS BRAINLIESTTT)
:DDDDD
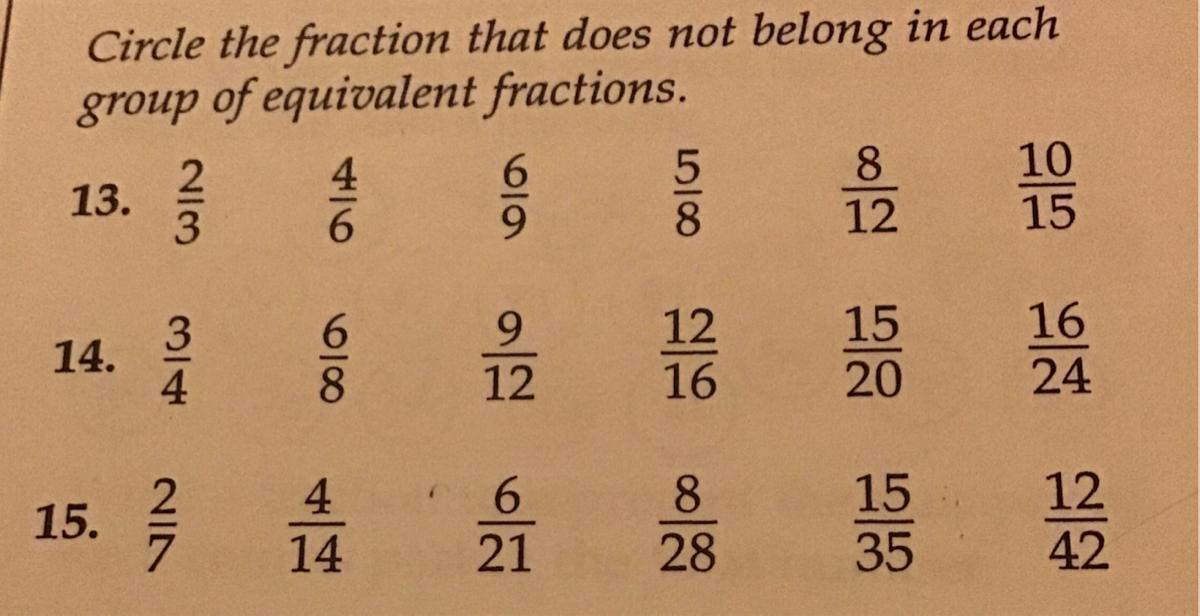
Answers
Answer:
13. 5/8
14. 16/24
15. 15/35
Answers:
13. 5/8
\(\frac{5}{8} \neq \frac{2}{3}\)
14. 16/24
\(\frac{16}{24} \neq \frac{3}{4}\)
15. 15/35
\(\frac{15}{35} \neq \frac{2}{7}\)
suppose the length of maize ears has narrow sense heritability (h2) ( h 2 ) of 0.70. a population produces ears that have an average length of 28 cm c m , and from this population a breeder selects a plant producing 34- cm c m ears to cross by self-fertilization.
Answers
We can expect the mean length of ears in the next generation to be 31.6 cm.
It is given that the narrow sense heritability (h2) is 0.70, which means that 70% of the total variation in maize ear length is due to genetic factors.
Let the mean length of ears in the original population be µ and the mean length of ears in the selected plant be x. Then, we can use the formula for response to selection to find the expected mean length of ears in the next generation:
x' = µ + h2 * (x - µ)
Substituting the given values, we get:
x' = 28 + 0.70 * (34 - 28) = 31.6 cm
Therefore, we can expect the mean length of ears in the next generation to be 31.6 cm.
To know more about mean visit:
brainly.com/question/2046711
#SPJ4
Can you help me please?
Can you solve for each variable? (x, y, and z)

Answers
Answer:
x = 103
y = 103
z = 33
Step-by-step explanation:
The sum of all three interior angles is 180 degrees.
180 - 29 - 48 = 103
x = 103
The vertical angles are always congruent, so x = y.
y = 103
180 - 44 - 103 = 33
z = 33
Ramon drew boxplots to summarize the number of pages in each chapter of two books. The values of the interquartile ranges for these boxplots are the same. Which boxplot could represent this data?
Answers
Answer
look at the ss i sent to see the answer
Step-by-step explanation:

Find the distance from the point to the line. 33. (0, 0, 12); x = 4t, y = -2t, z = 2t
Answers
The distance from the point (0, 0, 12) to the line x = 4t, y = -2t, z = 2t is (8√15) / 3.
The distance from the point (0, 0, 12) to the line defined by x = 4t, y = -2t, z = 2t can be found using the formula for the distance between a point and a line in three-dimensional space.
The formula is given by:
Distance = |(P - Q) × V| / |V|,
where P is a point on the line, Q is the given point, V is the direction vector of the line, and × denotes the cross product.
In this case, we can choose any point on the line to represent P. Let's choose P as (4, -2, 2). The direction vector of the line is V = (4, -2, 2).
Using the formula, we can calculate the distance as follows:
Distance = |((0, 0, 12) - (4, -2, 2)) × (4, -2, 2)| / |(4, -2, 2)|.
Simplifying the expression, we get:
Distance = |(-4, 2, 10) × (4, -2, 2)| / |(4, -2, 2)|.
To find the cross product, we can use the determinant method:
((-4, 2, 10) × (4, -2, 2)) = [(2 * 2 - 10 * -2), (10 * 4 - (-4) * 2), ((-4) * (-2) - 2 * 4)]
= (4 - 20, 40 - (-8), 8 - 8)
= (-16, 48, 0).
Now we can substitute the values back into the distance formula:
Distance = |(-16, 48, 0)| / |(4, -2, 2)|.
Taking the magnitude of the vectors, we get:
Distance =\(\sqrt((-16)^2 + 48^2 + 0^2) / √(4^2 + (-2)^2 + 2^2)\)
= √(256 + 2304 + 0) / √(16 + 4 + 4)
= √2560 / √24
= 16√10 / 2√6
= 8√10 / √6
= (8√10 / √6) * (√6 / √6)
= (8√60) / 6
= (8√15) / 3.
Learn more about vector here:
https://brainly.com/question/24256726
#SPJ11
If the number of bacteria on the surface of your phone triples every hour and can be described by the exponential function: f(x)=1000x3^x
, complete the table of values to show how much bacteria is on your phone after 4 hours.

Answers
Answer: 81,000
Step-by-step explanation:
We can solve this by using the formula given.
If f(1)=1000x3^1, then 1,000x3=3,000
If f(2)=1000x3^2, then 3^2=9 and 1000x9=9000,
and so on,
Now, f(4) will equal 1000x3^4, and 3^4 is 3x3x3x3, which is 9x9 or 9^2, which would be equal to 81, and 81x1000=81,000
To complete the table of values for the exponential function f(x) = 1000*3^x, we can evaluate the function for x = 0, 1, 2, 3, and 4, since we are interested in the number of bacteria on the phone after 4 hours.
x f(x)
0 1000
1 3000
2 9000
3 27,000
4 81,000
Therefore, after 4 hours, there will be 81,000 bacteria on the surface of the phone, assuming the number of bacteria triples every hour and can be described by the exponential function f(x) = 1000*3^x.
#SPJ1
If h(x) = 6 – x, what is the value of (h circle h) (10)?
–4
–2
10
16
Answers
Answer:
10
Step-by-step explanation:
Here, we want to find the value of ;
h circle h(10)
This mean we are to put h in h, the find the function of 10
we have this as;
6-(6-x)
= 6-6 + x = x
Now, replace the x by 10; so we have h circle h(10)
3x^2 + 5 = ?
Please Help
Answers
Answer:
5?
Step-by-step explanation:
There is no value for x, but the y value for 0 would be 5.
A frog is jumping onto a lily pad. Its height, h (in feet), is recorded at various seconds, t, in the
table below. Write an equation for the curve of best fit, then estimate the height of the frog after 6
seconds.
1
0
2
1
4.5
6
2
3
6.5
4
6
Answers
The curve of best fit is an illustration of a quadratic regression
The equation of the curve of best fit is \(y = -\frac{17}{18}x^2 + \frac{17}3x + 2\), and the height of the frog after 6 seconds is 2 feet
How to determine the equation of the curve of best fit?To determine the equation of the curve of best fit, we make use of a graphing calculator
Using the graphing calculator, we have the following calculation summary
a = -17/18b = 17/3c = 2The equation of the curve of best fit is represented as:
\(y = ax^2 + bx + c\)
Substitute the values for a, b and c.
So, we have:
\(y = -\frac{17}{18}x^2 + \frac{17}3x + 2\)
After 6 seconds, the value of x is 6.
So, we have:
\(y = -\frac{17}{18} * 6^2 + \frac{17}3 * 6 + 2\)
Evaluate
\(y = 2\)
Hence, the height of the frog after 6 seconds is 2 feet
Read more about curve of best fit at:
https://brainly.com/question/25226042
Solve by forming a quadratic equation. 1. Two numbers, which differ by 3, have a product of 88. Find them.
Answers
Answer:
Step-by-step explanation:
x*(x-3) = 88x^2-3x-88 = 0-b+- √(b^2-4ac)/2a3+-√(9-4(1)(-88)/23+- √(9+352)/2a3+-√361/2a3+19/2 or 3-19/221/2 ir -16/2S.S = {21/2,-8}2 numbers that differ by 3 and have a product of 88 are 11 and 8.
Let's say that the very first figure is x and the next is y.
x - y = 3 -----> y=x-3 .........(i)
xy=88 .......(ii)
Substitute (i) to (ii)
xy=88
x(x-3)=88
x\(x^{2} - 3x = 88\\x^{2} - 3x - 88 = 0\)
(x+8)(x-11)=0
x+8=0 or x-11=0
x=-8 or x=11
Substitute x=-8 to (i)
y=x-3
y=-8-3=-11
Substitute x=11 to (i)
y=x-3
y=11-3=8
Thus, x = -8 and y =- 11 or x = 11 and y = 8
2 numbers that differ by 3 and have a product of 88 are 11 and 8.
A 2nd equation with the form ax2 + bx + c = 0 denotes a quadratic equation, where a, b, and c are real-number coefficients and a 0. For instance, if school administration decides to build a chapel with a floor size of 400 sq metres and a length that is two meters longer than its width, we will need the aid of a quadratic equation to determine the length and breadth.
To learn more about quadratic equations visit:
https://brainly.com/question/1863222
Mr. McElroy enjoys listening to his MP3 player, which has 2,000 songs in five different genres of music. He took a sample of the number of each type of song it played on two different one-hour sessions when it was set to play a random mix. The counts are shown in the table below. Which proportion would predict the number of jazz songs he has stored on his MP3 player? Listening Samples from Mr. McElroy’s MP3 Player Sample 1 Sample 2 Country 5 Country 3 Pop 4 Pop 3 Classical 3 Classical 5 Jazz 2 Jazz 4 Rock 6 Rock 5 StartFraction 6 over 20 EndFraction = StartFraction x over 2000 EndFraction StartFraction 3 over 20 EndFraction = StartFraction x over 2000 EndFraction StartFraction 2 over 4 Endfraction = StartFraction x over 2000 EndFraction StartFraction 3 over 40 EndFraction = StartFraction x over 2000 EndFraction
Answers
Suppose f(x, y, z) = x2 + y2 + z2 and W is the solid cylinder with height 5 and base radius 6 that is centered about the z-axis with its base at z : -1. Enter O as theta. - (a) As an iterated integral, F sav = 10% x^2+y^2+z12 dz dr de W with limits of integration A = 0 B = C= 0 D= 6 E = -1 F = (b) Evaluate the integral.
Answers
∫_A^B ∫_B^C ∫_D^E (10%)(x^2 + y^2 + z^12) dz dr dθ.
This represents the full iterated integral for F_sav over the given solid cylinder.
(a) The iterated integral for F_sav with the given limits of integration is as follows:
∫∫∫_W (10%)(x^2 + y^2 + z^12) dz dr dθ,
where the limits of integration are A = 0, B = C = 0, D = 6, and E = -1.
(b) To evaluate the integral, we begin with the innermost integration with respect to z. Since z ranges from -1 to 6, the integral becomes:
∫∫_D^E (10%)(x^2 + y^2 + z^12) dz.
Next, we integrate with respect to r, where r represents the radial distance from the z-axis. As the solid cylinder is centered about the z-axis and has a base radius of 6, r ranges from 0 to 6. Thus, the integral becomes:
∫_B^C ∫_D^E (10%)(x^2 + y^2 + z^12) dz dr.
Finally, we integrate with respect to θ, where θ represents the angle around the z-axis. As the cylinder is symmetric about the z-axis, we integrate over a full circle, so θ ranges from 0 to 2π. Hence, the integral becomes:
∫_A^B ∫_B^C ∫_D^E (10%)(x^2 + y^2 + z^12) dz dr dθ.
This represents the full iterated integral for F_sav over the given solid cylinder.
The problem asks for the iterated integral of F_sav over the solid cylinder W. To evaluate this integral, we use the cylindrical coordinate system (r, θ, z) since the cylinder is centered about the z-axis. The function inside the integral is 10% times the sum of squares of x, y, and z^12. By integrating successively with respect to z, r, and θ, and setting appropriate limits of integration, we obtain the final iterated integral. The integration limits are determined based on the given dimensions of the cylinder.
Learn more about solid cylinder here:
https://brainly.com/question/30269341
#SPJ11
please answer the question in the picture!
|
|
|
v

Answers
Answer:
B is correct
Step-by-step explanation:
Hope I helped you and have an amazing day
Please help. I dont understand a thing. lol

Answers
Answer:
39 in²
Step-by-step explanation:
Area of triangle = 1/2 * b * h, where,
b = Base of Triangle
h = Height of triangle
Area of 4 triangles = 4 * 1/2 * 3 in * 5in
Area of 4 triangles = 2 * 3 in * 5 in
Area of 4 triangles = 30 in²
Area of square = a², where,
a = Each side of square.
Area of square = (3 in) ²
Area of square = 9 in²
Total surface area of pyramid = 30 inch² + 9 inch²
Total surface area of pyramid = 39 in²
Answer:
39 in^2 (Please mark me brainliest)
Step-by-step explanation:
3*3+3*2*5
=39
How many numbers among 1000-2000 are multiples of any two but not three of the first three odd prime numbers?
Hint: the first three odd prime numbers are 3,5,7
Answers
Answer: The first three odd prime numbers are 3, 5, and 7. A number is a multiple of two but not three of these prime numbers if it is divisible by two of them, but not the third.
To find the number of numbers between 1000 and 2000 that are multiples of two but not three of the first three odd prime numbers, we can count the number of multiples of each pair of prime numbers and subtract the number of multiples of all three prime numbers.
There are 200 multiples of 3 and 5 between 1000 and 2000 (200 numbers for each, for a total of 200 * 2 = 400). There are 133 multiples of 3 and 7 between 1000 and 2000 (133 numbers for each, for a total of 133 * 2 = 266). There are 80 multiples of 5 and 7 between 1000 and 2000 (80 numbers for each, for a total of 80 * 2 = 160). There are no multiples of all three prime numbers between 1000 and 2000.
Thus, the total number of numbers between 1000 and 2000 that are multiples of two but not three of the first three odd prime numbers is 400 + 266 + 160 = 826.
Step-by-step explanation:
which of choices (a) through (d) is not a condition for performing a significance test about a population proportion p?
Answers
Answer: The answer is D
Step-by-step explanation: I hope this helps!
Write 36 as a product of its prime factors. Write them In order smallest to largest.
Answers
1+1=?
help plz
i dont have enogh characters so this is what I have to type
Answers
Answer:
real answer 2
Step-by-step explanation:
the answer is 7 in my mind but sometimes it might be 11
help me pls !!! I’ll give good pts

Answers
Answer:
0.32×0.5=0.16
Can someone help me please

Answers
The domain of the function will therefore be 0≤x<∞
Domain of a functionDomain of a function are the independent value for which a function exists. Given the function below;
f(x) = \(\sqrt[4]{x}\)
Since the value in the root cannot be negative hence the domain of the function will be all positive real numbers.
The domain of the function will therefore be 0≤x<∞
Learn more on domain here: https://brainly.com/question/25959059
#SPJ1
What is meant by a stratified sample?
Answers
Answer:
A stratified random sampling involves dividing the entire population into homogeneous groups called strata (plural for stratum). Random samples are then selected from each stratum. ... A random sample from each stratum is taken in a number proportional to the stratum's size when compared to the population.
Answer:
Sampling that is used to represent different groups depending on their different qualities.
Hope that helps. x
The total cost to pay for parking at a state park for the day and rent a paddleboat are shown. Number of Hours Cost (5) 1 $17 2 $29 3 $41 4 $53 Part 1 Find the cost to park for a day and the hourly rate to rent a paddleboat. The cost to park for a day Is $ 5 and the hourly rate to rent a paddleboat is $ 12 Part 2 out of 2 What will Lin pay if she rents a paddleboat for 3.5 hours and splits the total cost with a friend? Complete the explanation. The total cost to rent the boat will be hours per hour + $ friend, they will each pay $ 1+2= If she splits the cost with a
Answers
We have the following:
The total cost to rent the boat will be:
3.5 hours x $ 12 per hour + $ 5 = $ 47. If she splits the cost with a friend, they each play $ 47 / 2 = $ 23.5
30 pointsss
At the neighborhood playground, your friend sits on a swing and gets pulled back by you to the highest point that you can reach. When you let go, your friend rides the swing without receiving or providing additional push. Your friend travels along an arc of 14 feet on the first swing (back to front). As the swing comes backwards, the length of the arc is .80 of the previous swing. This continues: each successive arc created by swinging is .80 of the previous swing.
a. Find the length of the arc for the 5th swing (the 5th arc). Round to the thousandths place.
b. On which swing is the length of the arc first less than 1 foot?
c. Find the total distance your friend travels in all of the swings up to and including the swing in answer to letter b.
Answers
Answer:
5th swing: 5.734 ft13 swing is less than 1 ft66.152 feet traveled in 13 swingsStep-by-step explanation:
The sequence of arc lengths is a geometric sequence with first term 14 ft and common ratio 0.8. The general (n-th) term of such a sequence is given by ...
an = a1 · r^(n-1) . . . . . . . first term a1, common ratio r
For this scenario, the n-th term is ...
an = 14·0.8^(n-1)
__
a.The 5th term is ...
a5 = 14·0.8^(5-1) ≈ 5.734 . . . . feet
__
b.For the arc length to be less than 1 ft, we require ...
14·0.8^(n-1) < 1
0.8^(n-1) < 1/14
(n -1)log(0.8) < log(1/14) . . . . . . note that these log values are negative
n -1 > log(1/14)/log(0.8)
n > 1 +log(1/14)/log(0.8) ≈ 12.8
The 13th swing will have an arc length less than 1 ft.
__
c.The sum of n terms of a geometric sequence is given by ...
Sn = a1 · (1 -r^n)/(1 -r)
13 terms of our sequence will total ...
S13 = 14 · (1 -0.8^(13))/(1 -0.8) ≈ 66.152 . . . feet
The total distance traveled in 13 swings is about 66.152 feet.
write a tbh about me ;)
p.s. love u guys
Answers
Answer:
tbh- you seem like you would be funny,nice, and pretty
Step-by-step explanation: Love ya ;)
Refer to Exercise 17. a. Predict the total numbers of people who reported an earthquake 9 minutes and 15 minutes after it ended. b. The table shows the actual data. Describe the accuracy of your extrapolations in part (a). Minutes,x=9,15 People,y=2750,3200

Answers
The Correlation coefficient of the given data is 0.9889 and the linear regression equation is ŷ = 381.07143X - 565.71429.
What is the correlation coefficient?A correlation coefficient is a statistical indicator of how well changes in one variable's value predict changes in another. When two variables are positively linked, the value either rises or falls together.
Given a Table of data where x is minutes after the earthquake and y is people noticed that
x y
1 10
2 100
3 400
4 900
5 1400
6 1800
7 2100
M: 4 M: 958.5714
Sum of X = 28
Sum of Y = 6710
Mean X = 4
Mean Y = 958.5714
Sum of squares (SSX) = 28
Sum of products (SP) = 10670
Regression Equation = ŷ = bX + a
b = SP/SSX = 10670/28 = 381.07143
a = MY - bMX = 958.57 - (381.07*4) = -565.71429
Thus, the linear equation is ŷ = 381.07143X - 565.71429
For correlation coefficient
X Values
∑ = 28
Mean = 4
∑(X - Mx)2 = SSx = 28
Y Values
∑ = 6710
Mean = 958.571
∑(Y - My)2 = SSy = 4158085.714
X and Y Combined
N = 7
∑(X - Mx)(Y - My) = 10670
R Calculation
r = ∑((X - My)(Y - Mx)) / √((SSₓ)(SS))
r = 10670 / √((28)(4158085.714)) = 0.9889
Meta Numerics (cross-check)
r = 0.9889
Thus the correlation coefficient for the given data is 0.9889.
Learn more about correlation coefficient here:
https://brainly.com/question/15577278
#SPJ2


Leah rides her bike to school a total of 80.75 miles per week. The miles (m) she rides in one day can be calculated using the equation below.
5m=80.75
Answers
Answer: 16.15
Step-by-step explanation:
Divide by 5 on both sides
m=16.15
If Z is the centroid of AWXY, WR = 87, SY =
and YT= 48, find each missing measure.
39,
a) WZ =
b) ZR=________
c) ZT=
d) YZ=
118
W
R
T
Answers
The measures of each term are; WS=39, WY=78, WZ=58, ZR=29, ZT=16 and YZ=32.
WE are given that Z is the centroid of triangle. Since centroid is the centre point of the object. The point in which the three medians of the triangle intersect is the centroid of a triangle.
Given WR=87 SY=39 and YT=48
WS=39
As WS=WR
WY=WS+SY
WY=39+39=78
WZ=58
Now, ZR=WR-WZ
ZR=87-48=29
ZT=16
Similalry;
YZ=YT-ZT
=48-16=32
YZ=32
Hence, the measures are; WS=39, WY=78, WZ=58, ZR=29, ZT=16 and YZ=32
To learn more on Triangles click:
brainly.com/question/2773823
#SPJ1
What is the solution to the system of linear equations?

Answers
Answer:
(0,2)
Step-by-step explanation:
The equations must be derived from the graph:
First, find the slope of f(x):
\(m=\frac{y_2-y_1}{x_2-x_1}\) let \((x_1,y_1)=(-3,3)\) and \((x_2,y_2)=(3,1)\)
\(m=\frac{(1)-(3)}{(3)-(-3)}\\m=\frac{-2}{6}\\m=-\frac{1}{3}\)
Then use \(y-y_1=m(x-x_1)\)
\(y-3=-\frac{1}{3}[x-(-3)]\\y-3=-\frac{1}{3}x-1\\y=-\frac{1}{3}x+2\\f(x)=-\frac{1}{3}x+2\)
For g(x), let:
\((x_1,y_1)=(-3,0)\\(x_2,y_2)=(0,2)\)
\(m=\frac{(2)-(0)}{(0)-(-3)}\\m=\frac{2}{3}\)
\(y-0=\frac{2}{3}[x-(-3)]\\y=\frac{2}{3}x+2\\g(x)=\frac{2}{3}x+2\)
Now, to solve for x, allow the two expressions written in terms of x equal each other.
\(-\frac{1}{3}x+2=\frac{2}{3}x+2\\(-\frac{1}{3}x+2)+\frac{1}{3}x=(\frac{2}{3}x+2)+\frac{1}{3}x\\2=x+2\\(2)-2=(x+2)-2\\x=0\)
To solve for y, substitute 0 for x in f(x):
\(y=-\frac{1}{3}x+2\\y=-\frac{1}{3}(0)+2\\y=0+2\\y=2\)
So, the solution to this system of equations would be the ordered pair (0,2). This solution is seen on the graph as the intersection of the two lines.
A firm has a loss level EBIT of $175m and an expected EBIT of $200m with a standard deviation of $50m. What is the z-score? What is the probability that the firm WILL have a negative EPS? A z-score of -1.20 would be entered as - 1.20. A probability of 37.25% should be entered as 37.25.
Answers
The required z-score is -0.5 and the probability that the firm WILL have a negative EPS is 30.85%.
Firm has a loss level EBIT of $175m and an expected EBIT of $200m with a standard deviation of $50m.
Z-score = (EBIT - Expected EBIT) / Standard deviation= (175 - 200) / 50= -0.5
Probability of having a negative EPS:
To find the probability that the firm will have a negative EPS, we need to find the area to the left of Z-score. As the Z-score is negative, we will be finding the left-tail probability using the standard normal table from the link below:
The area to the left of Z-score (0.5) is 0.3085 or 30.85%.
Therefore, the probability that the firm WILL have a negative EPS is 30.85%.
Learn more about EBIT at
https://brainly.com/question/15053243
#SPJ11