Answers
Given:
A function
\(f(x)=-2x^2+9\)and value of g(x) at x.
To find:
Maximum value of both functions.
Explanation:
For criticle points find f'(x) = 0 and f''(x)>0. Then value will be maximum.
Solution:
Now, first derivative is
\(\begin{gathered} f^(x)=-2x^2+9 \\ f^{\prime}(x)=-4x \end{gathered}\)Now, put f'(x)=0 and criticle point will be 0.
Now,
\(f^{^^{\prime}^{\prime}}(x)=-4\)As second derivative of function is negetive at x=0. So, we will get maximum at x=0
So, At x=0
\(f(0)=9\)So, maximum value of f(x) is 9 and maximum value of g(x) is 11.
Hence, this is the maximum values of f(x) and g(x).
Related Questions
Reuben made a shirt using 7/8yards of red fabric and 1/4yards of yellow fabric. How many more yards of red fabric did Reuben use?
Answers
Answer and Step-by-step explanation:
To find out how many more yards of red fabric Reuben used, we need to subtract the amount of yellow fabric from the amount of red fabric. Since the two fractions have different denominators, we need to find a common denominator before subtracting them. The least common multiple of 8 and 4 is 8, so we can rewrite both fractions with a denominator of 8:
7/8 - 1/4 = 7/8 - (1/4) * (2/2) = 7/8 - 2/8 = (7 - 2)/8 = 5/8
So, Reuben used 5/8 yards more red fabric than yellow fabric.
Write a fraction that is equivalent to 3/5 that has a denominator of 20.
5
15
20
20
12
12
20
3
20
Answers
Answer:
12/20
Step-by-step explanation:
\(\displaystyle \frac{3}{5}=\frac{3}{5}\cdot\frac{4}{4}=\frac{12}{20}\)
The answer is:
12/20In-depth-explanation:
The denominator of 3/5 is 5. To get from 5 to 20, we multiply it by 4.
We need to multiply both the numerator and the denominator by 4, so we do this:
\(\sf{\dfrac{3\times4}{5\times4}}\)
\(\sf{\dfrac{12}{20}}\)
Hence, the answer is 12/20.Ryanair provides cheap flights in Europe but prides itself on their on-time record. Ryanair quotes a flight time of 2 hours, 5 minutes. Suppose we believe that actual flight times are uniformly distributed between 2 hours and 2 hours, 20 minutes.
What is the expected flight time in minutes?
Answers
Answer:
The expected flight time is 2 hours 10 minutes
Step-by-step explanation:
Given
\(a = 2\ hours\)
\(b = 2\ hours\ 20\ mins\)
Required
The expected flight time
To do this, we simply calculate the mean using:
\(Mean = \frac{a + b}{2}\)
So, we have:
\(Mean = \frac{2\ hours + 2\ hours\ 20\ mins}{2}\)
\(Mean = \frac{4\ hours\ 20\ mins}{2}\)
\(Mean = 2\ hours\ 10\ mins\)
you went to a coffee house with 2 friends and ordered an iced coffee and dessert which came to $12.96 how much is the tip if the rate is 15%
Answers
Answer:
its 1.944
Step-by-step explanation:
Percentage can be calculated by dividing the value by the total value, and then multiplying the result by 100. The formula used to calculate percentage is: (value/total value)×100%.
which pair of pairs of polygons are congruent.

Answers
Answer:
bottom left. (arrow shaped)
Step-by-step explanation:
congruent shapes are the same size and shape
Jane's flight to an all-star track meet was cancelled due to a storm. The airline gave Jane a
voucher for $10 to spend at any vendor in the airport. Jane can only use the voucher at one
vendor and, according to the voucher rules, no change will be given. Any money not spent on
the voucher is lost. If a bottle of soda costs $2.50 plus an additional 6% sales tax, how many
bottles of soda could Jane buy? *
Answers
Answer:
3
Step-by-step explanation
3 x 2.50 = 7.50
7.50 x 0.06 = 0.45
7.50 + 0.45 = 7.95
So, she would be able to buy 3 sodas and it would cost $7.95
There are 5,280 feet in a mile. What is the number of the feet rounded to the nearest thousand?
Answers
Answer:
5000
Step-by-step explanation:
because 5280 minus 280 is 5000 and if u add 720 that is more than 720 so 5000 is correct
A non-scale model of the earth has a diameter of 18 in. Within an outer clay layer, there is a core made of a ball with a diameter of 3 in. What is the volume of the clay? use 3. 14 to approximate pi. Round to the nearest hundredth if necessary. Enter your answer as a decimal in the box.
Answers
Step-by-step explanation:
the answer is simply the volume of the whole model minus the volume of the core ball.
the volume of a sphere (ball, ...) is
4/3 × pi×r³
the radius is always half of the diameter.
radius of the whole model = 18/2 = 9 in.
radius of the core ball = 3/2 = 1.5 in.
so, we have as volume of the clay
4/3 × 3.14 × 9³ - 4/3 × 3.14 × 1.5³ =
= 4/3 × 3.14 × (9³ - 1.5³) = 4/3 × 3.14 × (729 - 3.375) =
= 4/3 × 3.14 × 725.625 = 3,037.95 in³
The angle of elevation to an airplane viewed from the control tower at an airport is 15°. The tower is 100 feet high and Pilot Cory reports that the altitude of the airplane is 5100 feet (5000 feet higher than the control tower). How far away (ground distance) from the control tower is the airplane?
Answers
Answer:
Given: Angle of elevation 15°AB (height of tower)=100AE=?CE = 5100 (5000 feet heigher than the tower)Now,
tan15°=
\( \frac{5100}{ae} \)
ae=
\( \frac{5100}{tan15} \)
.: ae = 19033.45
.: the aeroplane is 19033.45 m away from the control tower.

Pencil boxes cost $15 each. Calculators cost $24 each. Kelly bought a total of 100 pencil boxes and calculators for $2130. How many pencil boxes did she buy?
Answers
Answer:
Step-by-step explanation:
Kelly bought a total of 1500 pencil boxes.
The marked price of a mobile set is Rs3500 and the shopkeeper allows of 10%discount? (I) find the amount of discount. (ii)How much should a customer pay for it after discount.
Answers
Step-by-step explanation:
3500 × 10/100
rs. 350 is the discount
and to find the amnt the customer should pay subtract 350 from 3500
which is,
3150 Rupees
Please Help me with this

Answers
Answer:
it would be -2/3
since the equation layout is formated like this:
F/G(-1)
you multiply -1 by everything.
What is the central angle(pic included)
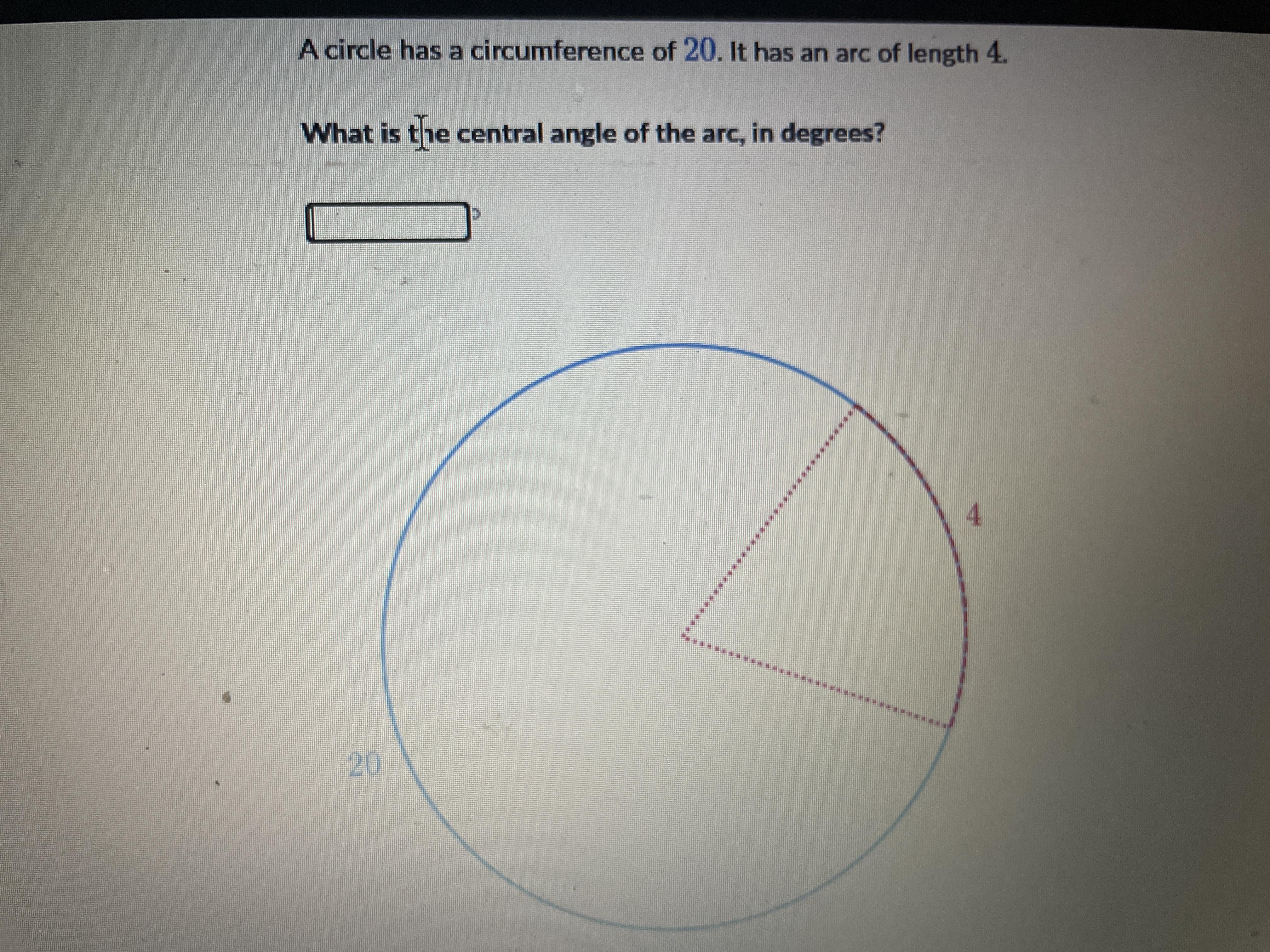
Answers
Answer:
72
Step-by-step explanation:
circumference = 20
arc = 4
4/20 =1/5
a circle = 360°
1/5 * 360 = 72
Please someone help!
this is adding polynomials.
h(x)+g(x)
h(x)=6x^2+4x^4+7x
Answers
\( {7x}^{4} + {12x}^{2} + 3x\)
Martin wants to build an additional closet in a corner of his bedroom. Because the closet will be in a corner, only two new walls need to be 1 built . The total length of the two new walls must be 12 m.
Martin wants the length of the closet to be twice as long as the width, as shown in the diagram.
b) Let the function f(l) be the sum of the length and the width. Find the equation for f(1).
c) Graph y = f(l).
d) Find the desired length and width. ile riding a
Answers
The relationship between the length & the width of the closet and the length of the wall is an illustration of a linear equation.
The equation for f(l) is: \(f(l) = 1.5l\).The desired length and width are 8m and 4mGiven that:
\(l = 2w\)
Divide both sides by 2
\(w = 0.5l\)
Equation of f(l)
The sum of the length and the width is represented as: f(l).
So, we have:
\(f(l) = l + w\)
Substitute \(w = 0.5l\)
\(f(l) = l + 0.5l\)
\(f(l) = 1.5l\)
See attachment for the graph of f(l)
The desired dimension
From the question, we understand that the total length is 12m.
This means that:
\(f(l) = 12\)
So, we have:
\(1.5l = 12\)
Divide both sides by 1.5
\(l = 8\)
Recall that:
\(w = 0.5l\)
\(w = 0.5 \times 8\)
\(w = 4\)
Hence, the desired length and width are 8m and 4m, respectively.
Read more about linear equations at:
https://brainly.com/question/2263981

The depth of a local river averages 16 ft, which is represented as |−16|. In January, it measured 4 ft deep, or |−4|, and in July, it was 18 ft, or |−18|. What is the difference between depths in January and July?
22 feet
14 feet
10 feet
2 feet
Answers
The difference between depths in January and July is 14 feets
The depth of a local river averages 16 ft., which is represented as |−16|.
In January, The depth of a local river measured 4 ft. deep, or |−4|
in July, The depth of a local river 18 ft., or |−18|
The average depth of a local river is measured as -16 because it is below the ground level and hence measured or plotted on -y axis
the difference between depths in January and July can be measured as
|−18| - |−4|
This is absolute sign which means every number inside this sign should be treated as positive
18 - 4 = 14
Hence, the difference between depths in January and July is 14 feets
To know more about Absolute sign -https://brainly.com/question/19538029
#SPJ1
Which has a greater effect on the volume-changing the radius by a given amount or changing the height by the same amount? Why?
Answers
Answer: Changing the radius of an object by a given amount has a greater effect on the volume than changing the height by the same amount. The volume of a cylinder is given by the formula V = πr²h, where V is the volume, r is the radius, and h is the height. If we change the radius by a given amount, say x, the new radius would be r+x. Hence, the new volume would be V' = π(r+x)²h = π(r²+2rx+x²)h = V + 2πrxh + πx²h. We can see that the volume change equals 2πrxh + πx²h. The first term is proportional to both the radius and the height, whereas the second term is proportional to the square of the radius and the height. Assuming that the height change is also x, the new volume would be V'' = πr²(h+x) = V + πr²x. We can see that the volume change is proportional to the radius squared and the change in height. Therefore, changing the radius by a given amount has a greater effect on the volume than changing the height by the same amount.
Enter an expression to make a true equation. (xyz)^2 - 1 = (____) x (xyz - 1)
I have a Algebra EOC tomorrow, and this question is from a practice test, but I am iffy on how I should answer. Can someone help?

Answers
The expression to make a true equation: (xyz)² - 1 = (____) x (xyz - 1) is (xyz + 1) using difference of two squares.
What is the difference of two squaresConsidering two numbers a and b, the difference of their squares written as a² - b² is equal to the the product of the sum of the numbers and the difference of the numbers, that is (a + b)(a - b).
From the question, the expression: (xyz)² - 1 can be expressed as the difference of two square as follows:
(xyz)² - 1 = (xyz)² - 1
(xyz)² - 1 = (xyz - 1) × (xyz + 1)
Therefore, the expression (xyz + 1) will make the equation: (xyz)² - 1 = (____) x (xyz - 1) true using difference of two squares.
Read more about difference of two squares here: https://brainly.com/question/15014357
#SPJ1
Calculate the product
20 (-15)
Answers
Answer:
Step-by-step explanation:
Product means multiply.
-300
Find the area of the triangle.
b ft
h yd
Question content area bottom
Part 1
The area of the triangle is
enter your response here or
enter your response here .
Answers
The area of the triangle is 52.32 square units
Finding the area of the trianglefrom the question, we have the following parameters that can be used in our computation:
The triangle (see attachment)
The base of the triangle is calculated as
base = 12 * tan(36)
The area of the triangle is then calculated as
Area = 1/2 * base * height
Where
height = 12
So, we have
Area = 1/2 * base * height
Substitute the known values in the above equation, so, we have the following representation
Area = 1/2 * 12 * tan(36) * 12
Evaluate
Area = 52.32
Hence, the area of the triangle is 52.32 square units
Read more about area at
brainly.com/question/24487155
#SPJ1

What is the perimeter of the woods, in miles? Round
you
answer to the nearest tenth.

Answers
The perimeter of the woods is 26 miles if each grid represents one mile in the figure.
What is the area of the rectangle?It is defined as the space occupied by the rectangle which is planner 2-dimensional geometry.
The formula for finding the area of a rectangle is given by:
Area of rectangle = length × width
We know the perimeter of the rectangle = 2(length + width)
As we can see closely in the figure the perimeter of the wood is actually a perimeter of a rectangle if we shift vertical and horizontal lines to make it a complete rectangle.
Let's suppose each grid is expressing one mile.
So the length of the rectangle = 9 miles
The width of the rectangle = 4 miles
The perimeter of the woods = 2(9+4) = 26 miles
Thus, the perimeter of the woods is 26 miles if each grid represents one mile in the figure.
Learn more about the rectangle here:
https://brainly.com/question/15019502
#SPJ1
Please help!!!! Tell me whether it’s a equation or not pleasr

Answers
Show that there is no positive integer 'n' for which Vn-1+ Vn+1 is rational

Answers
By contradiction we can prove that there is no positive integer 'n' for which √(n-1) + √(n+1) is rational.
Given: To show that there is no positive integer 'n' for which √(n-1) + √(n+1) rational.
Let us assume that √(n-1) + √(n+1) is a rational number.
So we can describe by some p / q such that
√(n-1) + √(n+1) = p / q , where p and q are some number and q ≠ 0.
Let us rationalize √(n-1) + √(n+1)
Multiplying √(n-1) - √(n+1) in both numerator and denominator in the LHS we get
{√(n-1) + √(n+1)} × {{√(n-1) - √(n+1)} / {√(n-1) - √(n+1)}} = p / q
=> {√(n-1) + √(n+1)}{√(n-1) - √(n+1)} / {√(n-1) - √(n+1)} = p / q
=> {(√(n-1))² - (√(n+1))²} / {√(n-1) - √(n+1)} = p / q
=> {n - 1 - (n + 1)] / {√(n-1) - √(n+1)} = p / q
=> {n - 1 - n - 1} / {√(n-1) - √(n+1)} = p / q
=> -2 / {√(n-1) - √(n+1)} = p / q
Multiplying {√(n-1) - √(n+1)} × q / p on both sides we get:
{-2 / {√(n-1) - √(n+1)}} × {√(n-1) - √(n+1)} × q / p = p / q × {√(n-1) - √(n+1)} × q / p
-2q / p = {√(n-1) - √(n+1)}
So {√(n-1) - √(n+1)} = -2q / p
Therefore, √(n-1) + √(n+1) = p / q [equation 1]
√(n-1) - √(n+1) = -2q / p [equation 2]
Adding equation 1 and equation 2, we get:
{√(n-1) + √(n+1)} + {√(n-1) - √(n+1)} = p / q -2q / p
=> 2√(n-1) = (p² - 2q²) / pq
squaring both sides
{2√(n-1)}² = {(p² - 2q²) / pq}²
4(n - 1) = (p² - 2q²)² / p²q²
Multiplying 1 / 4 on both sides
1 / 4 × 4(n - 1) = (p² - 2q²)² / p²q² × 1 / 4
(n - 1) = (p² - 2q²)² / 4p²q²
Adding 1 on both sides:
(n - 1) + 1 = (p² - 2q²)² / 4p²q² + 1
n = (p² - 2q²)² / 4p²q² + 1
= ((p⁴ - 4p²q² + 4q⁴) + 4p²q²) / 4p²q²
= (p⁴ + 4q⁴) / 4p²q²
n = (p⁴ + 4q⁴) / 4p²q², which is rational
Subtracting equation 1 and equation 2, we get:
{√(n-1) + √(n+1)} - {√(n-1) - √(n+1)} = p / q - (-2q / p)
=>√(n-1) + √(n+1) - √(n-1) + √(n+1) = p / q - (-2q / p)
=>2√(n+1) = (p² + 2q²) / pq
squaring both sides, we get:
{2√(n+1)}² = {(p² + 2q²) / pq}²
4(n + 1) = (p² + 2q²)² / p²q²
Multiplying 1 / 4 on both sides
1 / 4 × 4(n + 1) = (p² + 2q²)² / p²q² × 1 / 4
(n + 1) = (p² + 2q²)² / 4p²q²
Adding (-1) on both sides
(n + 1) - 1 = (p² + 2q²)² / 4p²q² - 1
n = (p² + 2q²)² / 4p²q² - 1
= (p⁴ + 4p²q² + 4q⁴ - 4p²q²) / 4p²q²
= (p⁴ + 4q⁴) / 4p²q²
n = (p⁴ + 4q⁴) / 4p²q², which is rational.
But n is rational when we assume √(n-1) + √(n+1) is rational.
So, if √(n-1) + √(n+1) is not rational, n is also not rational. This contradicts the fact that n is rational.
Therefore, our assumption √(n-1) + √(n+1) is rational is wrong and there exists no positive n for which √(n-1) + √(n+1) is rational.
Hence by contradiction we can prove that there is no positive integer 'n' for which √(n-1) + √(n+1) is rational.
Know more about "irrational numbers" here: https://brainly.com/question/17450097
#SPJ9
Can someone help me with this.

Answers
Answer:
100,000,000
Step-by-step explanation:
to evaluate means to calculate so
10^8 is really 1 with 8 zeros
please help me ASAP!!!

Answers
Answer:
18
Step-by-step explanation:
parallel lines cut by a transversal are proportional, thus we can set up a ratio to solve for the missing value
7/14 = 9/x
7x = 126
x = 18
From 86 books to 150 books, what's the percent increase?
Answers
because 150 - 86 = 64 / 86 = 0.74418605 x 100 = 74.42 % !!
hope that helps you :D
NO LINKS!!! URGENT HELP PLEASE!!!
State if the given functions are inverses.
1. g(x) = 4 + (7/2)x
f(x) = 5 - (4/5)x
Find the inverses of each function.
2. g(n) = (8/3)n + 7/3
3. g(x) = 1 - 2x^3
Answers
Answer:
1) The functions are not inverses.
\(\textsf{2)} \quad g^{-1}(n)=&\dfrac{3}{8}n-\dfrac{7}{8}\)
\(\textsf{3)} \quad g^{-1}(x)&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\)
Step-by-step explanation:
Question 1The inverse composition rule states that if two functions are inverses of each other, then their compositions result in the identity function.
Given functions:
\(g(x) = 4 + \dfrac{7}{2}x \qquad \qquad f(x) = 5 - \dfrac{4}{5}x\)
Find g(f(x)) and f(g(x)):
\(\begin{aligned} g(f(x))&=4+\dfrac{7}{2}f(x)\\\\&=4+\dfrac{7}{2}\left(5 - \dfrac{4}{5}x\right)\\\\&=4+\dfrac{35}{2}-\dfrac{14}{5}x\\\\&=\dfrac{43}{2}-\dfrac{14}{5}x\\\\\end{aligned}\) \(\begin{aligned} f(g(x))&=5 - \dfrac{4}{5}g(x)\\\\&=5 - \dfrac{4}{5}\left(4 + \dfrac{7}{2}x \right)\\\\&=5-\dfrac{16}{5}-\dfrac{14}{5}x\\\\&=\dfrac{9}{5}-\dfrac{14}{5}x\end{aligned}\)
As g(f(x)) or f(g(x)) is not equal to x, then f and g cannot be inverses.
\(\hrulefill\)
Question 2To find the inverse of a function, swap the dependent and independent variables, and solve for the new dependent variable.
Calculate the inverse of g(n):
\(\begin{aligned}y &= \dfrac{8}{3}n + \dfrac{7}{3}\\\\n &= \dfrac{8}{3}y + \dfrac{7}{3}\\\\3n &= 8y + 7\\\\3n-7 &= 8y\\\\y&=\dfrac{3}{8}n-\dfrac{7}{8}\\\\g^{-1}(n)&=\dfrac{3}{8}n-\dfrac{7}{8}\end{aligned}\)
Calculate the inverse of g(x):
\(\begin{aligned}y &= 1-2x^3\\\\x &= 1-2y^3\\\\x -1&=-2y^3\\\\2y^3&=1-x\\\\y^3&=\dfrac{1}{2}-\dfrac{1}{2}x\\\\y&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\\\\g^{-1}(x)&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\\\\\end{aligned}\)
Answer:
1.
If the composition of two functions is the identity function, then the two functions are inverses. In other words, if f(g(x)) = x and g(f(x)) = x, then f and g are inverses.
For\(\bold{g(x) = 4 + \frac{7}{2}x\: and \:f(x) = 5 -\frac{4}{5}x}\), we have:
\(f(g(x)) = 5 - \frac{4}{5}(4 + \frac{7}{2}x)\\ =5 - \frac{4}{5}(\frac{8+7x}{2})\\=5 - \frac{2}{5}(8+7x)\\=\frac{25-16-14x}{5}\\=\frac{9-14x}{5}\)
\(g(f(x)) = 4 + (\frac{7}{5})(5 - \frac{4}{5}x) \\=4 + (\frac{7}{5})(\frac{25-4x}{5})\\=4+ \frac{175-28x}{25}\\=\frac{100+175-28x}{25}\\=\frac{175-28x}{25}\)
As you can see, f(g(x)) does not equal x, and g(f(x)) does not equal x. Therefore, g(x) and f(x) are not inverses.
Sure, here are the inverses of the functions you provided:
2. g(n) = (8/3)n + 7/3
we can swap the roles of x and y and solve for y to find the inverse of g(n). In other words, we can write the equation as y = (8/3)n + 7/3 and solve for n.
y = (8/3)n + 7/3
n =3/8*( y-7/3)
Therefore, the inverse of g(n) is:
\(g^{-1}(n) = \frac{3}{8}(n - \frac{7}{3})=\frac{3}{8}*\frac{3n-7}{3}=\boxed{\frac{3n-7}{8}}\)
3. g(x) = 1 - 2x^3
We can use the method of substitution to find the inverse of g(x). We can substitute y for g(x) and solve for x.
\(y = 1 - 2x^3\\2x^3 = 1 - y\\x = \sqrt[3]{\frac{1 - y}{2}}\)
Therefore, the inverse of g(x) is:
\(g^{-1}(x) =\boxed{ \sqrt[3]{\frac{1 - x}{2}}}\)
Suppose there are 16 students in your class. If the teacher draws 2 names at random, what is the probability that you and your best friend will be chosen?
1/15
1/120
1/8
3/31
Answers
Answer:
The total number of ways to choose 2 students from a class of 16 is given by the combination formula:
C(16,2) = 16! / (2! * (16-2)!) = (1615) / (21) = 120
This means there are 120 possible pairs of students that could be drawn.
The probability of you and your best friend being chosen is the number of ways that you and your friend can be selected divided by the total number of possible pairs. There is only 1 way to select you and your best friend out of the class of 16, so the probability is:
P(you and your best friend are chosen) = 1/120
Therefore, the probability that you and your best friend will be chosen is 1/120. Option (B) is the correct answer.
Answer:
The probability of choosing one specific student out of 16 is 1/16. After one student is chosen, there are 15 students left, so the probability of choosing the second specific student out of the remaining 15 is 1/15. The probability of both events happening is the product of the probabilities: (1/16) x (1/15) = 1/240. However, there are two ways that the students can be chosen (your friend first, then you or you first, then your friend), so we need to multiply the probability by 2: 2 x (1/240) = 1/120. Therefore, the probability of you and your best friend being chosen is 1/120. Answer: 1/120.
write a fraction with a denominator of 9. The fraction should be less than half
Answers
Answer:
The only fraction i can think of is 2/9
Step-by-step explanation:
The 2010 U.S. Census asked every household to report information on each person living there. Suppose for a sample of 30 households selected, the number of persons living in each was reported as follows. 2 3 1 2 6 4 2 1 5 3 2 3 1 2 2 1 3 1 2 2 4 2 1 2 9 3 2 1 1 3 Compute the mean, median, mode, range, lower and upper quartiles, and interquartile range for these data. (Round the mean to 2 decimal places.) Mean
Answers
Answer:
\(\bar x =2.53\) -- Mean
\(Median= 2\)
\(Mode = 2\)
\(Range = 8\)
\(Q_1 = 1\)
\(Q_3 = 3\)
\(IQR = 2\)
Step-by-step explanation:
Given
n = 30
Data: 2 3 1 2 6 4 2 1 5 3 2 3 1 2 2 1 3 1 2 2 4 2 1 2 9 3 2 1 1 3
Solving (a): The mean
This is calculated as:
\(\bar x =\frac{\sum x}{n}\)
\(\bar x =\frac{2 +3 +1 +2 +6 +4 +2 +1 +5 +3 +2 +3+ 1+ 2 +2 +1 +3 +1 +2 +2 +4 +2 +1 +2 +9 +3 +2 +1 +1 +3}{30}\)
\(\bar x =\frac{76}{30}\)
\(\bar x =2.53\)
Solving (b): The median
First arrange the given data
Arranged: 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 4 4 5 6 9
\(Median =\frac{1}{2}(n+1)\)
\(Median =\frac{1}{2}(30+1)\)
\(Median =\frac{1}{2}(31)\)
\(Median = 15.5th\)
This implies that the median is the average of the 15th and 16th item
\(Median = \frac{2+2}{2}\)
\(Median = \frac{4}{2}\)
\(Median= 2\)
Solving (c): The mode
From the given data; 2 has the highest frequency of 11.
So,
\(Mode = 2\)
Solving (d): The Range
\(Range = Highest\ Data - Lowest\ Data\)
The highest is 9 and the lowest is 1,
So:
\(Range = 9 - 1\)
\(Range = 8\)
Solving (e): Lower (Q1) and Upper (Q3) quartile.
Q1 is calculated as:
\(Q_1 = \frac{1}{4}(n+1)th\)
\(Q_1 = \frac{1}{4}(30+1)th\)
\(Q_1 = \frac{1}{4}(31)th\)
\(Q_1 = 7.75th\)
\(Q_1 = 8th\ item\)
\(Q_1 = 1\) -- from the arranged data
Q3 is calculated as:
\(Q_3 = \frac{3}{4}(n+1)th\)
\(Q_3 = \frac{3}{4}(30+1)th\)
\(Q_3 = \frac{3}{4}(31)th\)
\(Q_3 = 23.25th\)
\(Q_3 = 23rd\ item\)
\(Q_3 = 3\) -- from the arranged data
Solving (f): The interquartile range (IQR)
\(IQR = Q_3 - Q_1\)
\(IQR = 3-1\)
\(IQR = 2\)
