Answers
The scale is 2.5, you can figure this out by 30/12 because they are corresponding legs, because the scale factor is 2.5, you will multiply 2.5x5.5. The 5.5 comes from 6 inches being one half of a foot.
Related Questions
Find the solution for a 2x2 matrix A:
[4 4
0 1] to the nth power = [ ]
Answers
Answer:
Step-by-step explanation:
Answer:
A^n = [4^n 4^n
0 1]
Step-by-step explanation:
To find the solution for the 2x2 matrix A:
[4 4
0 1] to the nth power = [ ]
We can use matrix multiplication to raise A to the nth power. Let's start with n = 1:
A^1 = [4 4
0 1]
Now, let's solve for A^2 by multiplying A^1 by A:
A^2 = A x A^1
= [4 4 [4 4
0 1] 0 1]
= [16 16
0 1]
Next, let's solve for A^3:
A^3 = A x A^2
= [4 4 [16 16
0 1] 0 1]
= [64 64
0 1]
We can see a pattern emerging:
A^1 = [4 4
0 1]
A^2 = [16 16
0 1]
A^3 = [64 64
0 1]
We can generalize this pattern as follows:
A^n = [4^n 4^n
0 1]
Therefore, the solution for the 2x2 matrix A raised to the nth power is:
A^n = [4^n 4^n
0 1]
[ (5 + 1) ((6-5))^2)]
Answers
Show that the point (å,ä ) is on the perpendicular bisector of the line segment with end points
(Ů,ü ) and (ĝ,ġ )
Answers
To show that the point (å, ä) is on the perpendicular bisector of the line segment with endpoints (Ů, ü) and (ĝ, ġ), we need to demonstrate two things: that the point lies on the line segment, and that it is equidistant from the endpoints.
1. Determine the midpoint of the line segment:
- The midpoint coordinates (\(x_{mid, y_{mid\)) can be found using the midpoint formula:
\(x_{mid\) = (x1 + x2) / 2 and \(y_mid\) = (y1 + y2) / 2, where (x1, y1) and (x2, y2) are the coordinates of the endpoints.
In this case, we have (x1, y1) = (Ů, ü) and (x2, y2) = (ĝ, ġ).
2. Calculate the midpoint coordinates:
- Substitute the values into the midpoint formula to find (x_mid, y_mid).
3. Find the slope of the line segment:
- Use the slope formula: slope = (y2 - y1) / (x2 - x1).
Apply the formula to the endpoints (Ů, ü) and (ĝ, ġ) to determine the slope of the line segment.
4. Determine the negative reciprocal of the line segment's slope:
- Take the negative reciprocal of the slope calculated in the previous step. The negative reciprocal of a slope m is -1/m.
5. Write the equation of the perpendicular bisector:
- Using the negative reciprocal slope and the midpoint coordinates (\(x_{mid\), \(y_{mid\)), write the equation of the perpendicular bisector in point-slope form: y - \(y_{mid\) = \(m_{perp\) * (x - \(x_{mid\)), where \(m_{perp\) is the negative reciprocal slope.
6. Substitute the point (å, ä) into the equation:
- Replace x and y in the equation of the perpendicular bisector with the coordinates of the point (å, ä). Simplify the equation.
7. Verify that the equation holds true:
- If the equation is satisfied when substituting (å, ä), then the point lies on the perpendicular bisector.
By following these steps, you can demonstrate that the point (å, ä) lies on the perpendicular bisector of the line segment with endpoints (Ů, ü) and (ĝ, ġ).
For more such questions on line segment, click on:
https://brainly.com/question/280216
#SPJ8
what is 4 and 5???????

Answers
Answer:
586 cm^3 and 486 in^2
Step-by-step explanation:
4) The volume of the triangular prims is (1/2)*(a*c*h) = 0.5*(8*9*16)=586 cm^3
5) Wrapping paper needed is equal to the surface area of the cube, 6s^2=486 in^2
Can you pls help meSimplify 6+(-11)
Answers
basically all you're doing here is subtracting 6 from 11. 11-6=5, add the - sign, so the answer is -5
PLEASE PLEASE HELP WILL MARK BRAINLIST!!!!!!!!!!!!

Answers
The function rule for g(x) is h(x) = (x - 0)² - 7.
How to determine the vertex form of a quadratic equation?In Mathematics, the vertex form of a quadratic function is represented by the following mathematical equation:
f(x) = a(x - h)² + k
Where:
h and k represents the vertex of the graph.a represents the leading coefficient.Based on the information provided about the vertex (0, -7) and other points (-3, 2), we can determine the value of a as follows:
f(x) = a(x - h)² + k
2 = a(-3 - 0)² - 7
2 + 7 = 9a
9 = 9a
a = 1
Therefore, the required quadratic function in vertex form is given by:
h(x) = a(x - h)² + k
h(x) = (x - 0)² - 7
h(x) = x² - 7
Read more on vertex here: brainly.com/question/14946018
#SPJ1
-2(y-4)=18 PLEASE HELPPPPPPP
Answers
Answer:
y = -5
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightDistributive Property
Equality Properties
Multiplication Property of Equality Division Property of Equality Addition Property of Equality Subtraction Property of EqualityStep-by-step explanation:
Step 1: Define
Identify
-2(y - 4) = 18
Step 2: Solve for y
[Distributive Property] Distribute -2: -2y + 8 = 18[Subtraction Property of Equality] Subtract 8 on both sides: -2y = 10[Division Property of Equality] Divide -2 on both sides: y = -5Which is more, 6 ounces or
1 / 2
of a pound?
Answers
*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆**☆*――*☆*――*☆*――*☆
Answer: 1/2 a pound is more, because 1/2 a pound is 8 ounces
I hope this helped!
<!> Brainliest is appreciated! <!>
- Zack Slocum
*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆**☆*――*☆*――*☆*――*☆
Answer:
1/2 of a pound.
Step-by-step explanation:
Its because 16 ounces = 1 pound, and 16/2 = 8, which is bigger than 6.
Find the amount of money accumulated after investing a principle P for years t at interest rate r, compounded continuously. P = $3,200 r = 8% t = 4
Answers
Answer:
The accumulated amount would be $4,353.56
Step-by-step explanation:
r= 0.08
A= 3, 200(1+0.08)^4
= 3,200(1.08)^4
= $4,353.56
if you take away 25 from a number you will be left with two and halftimes 30. what is the number?
Answers
If you take away 25 from (100) you get 75.
70 also equals 2.5*30
solve the system by elimination 4x-y=2 and x+3y=7
Answers
Answer:
x=1 y=2
Step-by-step explanation:
Isolate x for 4x -y=2: X=2+y/4
Substitute x= 2+y/4
(2+y/4 )+3y=7
simplify 2+13y/4=7
Isolate y for 2+13y/4=7
y=2
Forx= 2+y/4
Substitute y = 2
x= 2+2/4
Simplify
X=1
2.2 2.1.4 a Given that A and B are complementary angles and 7 cos A-3 = 0. Determine WITHOUT the use of a calculator, the value of: 7 cos B-3 tan A. (4)
Answers
Write an expression using the distributed property to dind the product of 7x63
Answers
The product of the expression 7 x 63 is 441.
We have,
To find the product of 7 x 63 using the distributive property, we can break down 63 as the sum of its factors, such as 60 and 3:
7 x 63 = 7 x (60 + 3)
Now, we can apply the distributive property by multiplying 7 to each term inside the parentheses:
7 x (60 + 3) = 7 x 60 + 7 x 3
Simplifying further:
7 x 60 + 7 x 3 = 420 + 21
Therefore,
The product of 7 x 63 is 441.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
15. Express 2/5 as a percentage
Answers
Answer:
\(40\%\)
Step-by-step explanation:
\( \frac{2}{5} \times 100 = 40\%\)
Divide 2 by 5 to get a decimal, then multiply the decimal by 100 to get a percent.
2/5 = 0.4
0.4x100 = 40
2/5 = 40%
look at attachment!!!!

Answers
Answer:
x = 5
Step-by-step explanation:
We know that BD = 2x - 1 and BC + CD = BD. Thus, we can set the sum of (x- 3) and 7 equal to 2x - 1 to find x:
BC + CD = BD
x - 3 + 7 = 2x - 1
x + 4 = 2x - 1
x + 5 = 2x
5 = x
Thus, x = 5
Checking the validity of our answer:
We can check that our answer is correct by plugging in 5 for x in x - 3 and 2x - 1 and checking that we get the same answer on both sides of the equation:
5 - 3 + 7 = 2(5) - 1
2 + 7 = 10 - 1
9 = 9
Thus, our answer is correct.
Simplify: (-4ab^2)(-3b^2c) (5a)
Answers
Answer:
\(60a^{2} b^{4} c\)
Step-by-step explanation:
just multiply first paranthesis with second one. They are each 1 unit as there are no addition or subtraction inside the parantehsis so DON'T distribute. It's more simple.
(12ab^4c)*(5a)
now multiply these 2 paranthesis, again just 2 units to multiple.
60a^2b^4c
A hiker starts at an elevation of 420 yards below sea level descends 1,400 yards and
before ascending for 4,600 yards. What is the elevation at the end of the hike?
Answers
Step by step:
420-1,400=-980
-980+4,600=3,620
By using graphical method, find optimal solution of the problem max z = 3x + y s.t 2x - y ≤ 5 -x + 3y ≤ 6 x ≥ 0, y ≥ 0
Answers
By analyzing the graph and evaluating the objective function at each vertex of the feasible region, we can find the optimal solution, which is the vertex that maximizes the objective function z = 3x + y.
To find the optimal solution of the given problem using the graphical method, we need to plot the feasible region determined by the given constraints and then identify the point within that region that maximizes the objective function.
Let's start by graphing the constraints:
1. Plot the line 2x - y = 5. To do this, find two points on the line by setting x = 0 and solving for y, and setting y = 0 and solving for x. Connect the two points to draw the line.
2. Plot the line -x + 3y = 6 using a similar process.
3. The x-axis and y-axis represent the constraints x ≥ 0 and y ≥ 0, respectively.
Next, identify the feasible region, which is the region where all the constraints are satisfied. This region will be the intersection of the shaded regions determined by each constraint.
Finally, we need to identify the point within the feasible region that maximizes the objective function z = 3x + y. The optimal solution will be the vertex of the feasible region that gives the highest value for the objective function. This can be determined by evaluating the objective function at each vertex and comparing the values.
Note: Without a specific graph or additional information, it is not possible to provide the precise coordinates of the optimal solution in this case.
For more such questions on graph
https://brainly.com/question/19040584
#SPJ8
Two students in different classes took the same math test. Both students received a
score of 87. In student A's class the mean was 78 and the standard deviation of 5. In
student B's class the mean was 76 with a standard deviation of 4. Which student
scored in the top 10% of their class?
Answers
Answer:
Both students scored in the top 10% of their classes.
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
In this question:
Top 10% = Above the 100 - 10 = 90th percentile.
The 90th percentile of scores is X when Z has a pvalue of 0.9, that is, Z = 1.28.
So, the student who had a z-score above 1.28 scored in the 90th percentile of their class.
In student A's class the mean was 78 and the standard deviation of 5. He scored 87.
We have that \(\mu = 78, \sigma = 5, X = 87\)
Then
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{87 - 78}{5}\)
\(Z = 1.8\)
1.8 > 1.28, so student A scored in the top 10% of his/her class.
Student B's class the mean was 76 with a standard deviation of 4. Scored 87.
We have that \(\mu = 76, \sigma = 4, X = 87\)
Then
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{87 - 76}{4}\)
\(Z = 2.75\)
2.75 > 1.28, so student B also scored in the top 10% of his/her class.
Both students scored in the top 10% of their classes.
Joselyn got 22 out of 25 questions correct on her math exam. What percent of the questions did she get correct?
Answers
Answer:
88 percent
Step-by-step explanation:
100/25 is 4 so 4 times 22 is 88 percent
can someone please help

Answers
Answer:
The measure of CD is 46
Step-by-step explanation:
From the midpoint theorem, we have,
FG = (1/2)CD
so,
\(13+5x=(1/2)(-3x+52)\\So,\\2(13+5x)=-3x+52\\26+10x=-3x+52\\13x=52-26\\13x=26\\x=26/13\\x=2\)
Now,
\(CD = -3x+52\\since \ x=2\\we \ get\\CD=-3(2) +52\\CD=-6+52\\CD=46\)
4/x = 2/7 please help ASAP!!
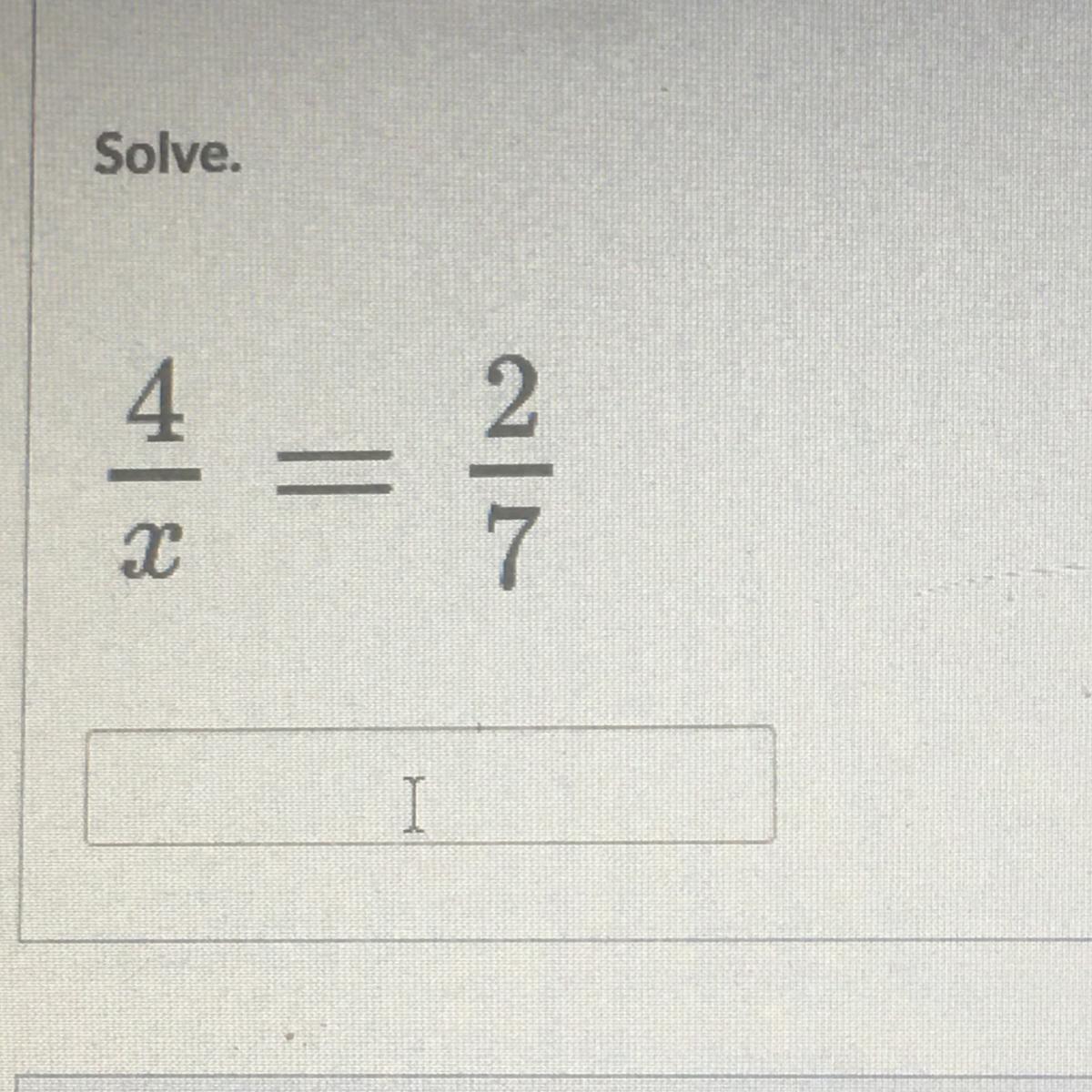
Answers
Answer:
use cross multiplication to solve
4*7 = 2*x (multiply)
28 = 2x (divide both sides by 2 to isolate x )
x = 14 (your answer)
Step-by-step explanation:
I hope this helped :)
Answer:
Step-by-step explanation:
Or,2×x=7×4
Or,2x=28
Or,x=14
Create an expression that has the same value as (6x-4) + (x + 5).
Write the correct numbers from the list in the blank boxes. Each number
may be used once, more than once, or not at all.
Answers
Answer: 7x + 1
Step-by-step explanation:
(6x-4)+(x+5)
Step 1: Remove Parentheses:
6x-4+x+5
Step 2: Combine Like Terms:
7x +1
2. Approximately 2% of the nation's children (about 1.7 million) have a parent who is in jail or prison. Let X be the number of children that have an incarcerated parent from a random sample of 100 children. (a) Verify that this is a binomial setting by identifying the four criteria in this problem. (b) Describe what P(X = 0) means in context. (c) Find P(X = 0) and P(X = 1). *
Answers
Answer:
2% 2% of the nation's children (about 1.7 million) have a parent who is in jail or prison.
What is the area of the shaded region?

Answers
Answer:
80 mm²
Step-by-step explanation:
Even for slanted triangles, the area is base x half height! The base is 10 mm, half the height is 8 mm, so the area is 8x10=80 mm.
Find the equation for the line through the point (7/5,1/12) that is perpendicular to the line 3x-4y=7. You may leave your answer in the point-slope form if you wish. If you use slope-intercept form, all fractions must be combined and reduced wherever possible.
Answers
The equation of the line is (y - 1/12) = -4/3(x - 7/5).
What is the slope of a line?
A line's slope in mathematics is defined as the ratio of the change in the y coordinates to the change in the x coordinate.
Both the net change in the y-coordinate and the net change in the x-coordinate are represented by y and x, respectively.
Consequently, the formula for the change in the y-coordinate with respect to the change in the x-coordinate is
m = y/x = y/x = change in y/change in x
where "m" represents a line's slope.
Additionally, the slope of the line can be depicted by
tan θ = Δy/Δx
So, the slope of a line is tan.
The given equation of a line is:
3x-4y=7
-4y = -3x + 7
y = 3/4 x - 7/4
The slope of the line is 3/4.
The slope of the line perpendicular to the given line is - 1/m = - 4/3
The point-slope of a line is y - y₁ = m(x - x₁).
The given point is (7/5,1/12)
The equation of the line is
(y - 1/12) = -4/3(x - 7/5)
To learn more about equation of line, click on the below link:
https://brainly.com/question/10853937
#SPJ1
(3w^2 + 7W + 2) + (w^2 + 2W + 8)
Answers
Answer:
4w^2+9w+10
Step-by-step explanation:
(3w^2+7w+10+w^2+2W
Combine like terms
4w^2+7w+10+2w
Combine like terms
4w^2+9w+10
Answer:
4w^2+9w+10
Step-by-step explanation:
Eastern Aviation Equipment pays Donald Simmons a $1760 monthly salary plus a 12% commission on merchandise he sells each month. Assume Donald's sales were $90,800 for last month. Calculate the following amounts:
1. Amount of Commission:
2. Gross Pay:
Answers
The equation that represent the gross pay is y = 0.12x + 1760. The commission was $10896 and gross pay was $12656
What is an equation?An equation consists of numbers and variables linked together by mathematical operations to form an expression.
A linear equation is in the form:
y = mx + b
Where m is the rate of change and b is the initial value
Let y represent the gross pay for x total sales.
Donald Simmons a $1760 monthly salary plus a 12% commission on merchandise he sells each month, hence:
y = 1760 + 12% of x
y = 0.12x + 1760
Donald's sales were $90,800 for last month. Hence:
a) Commission = 0.12 * $90800 = $10896
b) Gross pay:
y = 10896 + 1760 = $12656
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
What is the solution to the system of linear equations?
(–4.5, 4.25)
(–1.7, –2.8)
(0, –7)
(3, 0.5)
Answers
Answer:
−903.65625
Step-by-step explanation:
((((−4.5)(4.25))(−1.7−2.8))(0−7))((3)(0.5))
=((−19.125(−1.7−2.8))(0−7))((3)(0.5))
=(((−19.125)(−4.5))(0−7))((3)(0.5))
=86.0625(0−7)(3)(0.5)
=(86.0625)(−7)(3)(0.5)
=−602.4375(3)(0.5)
=(−602.4375)(1.5)
=−903.65625
if A and B are events with P(A) = 0.2, P(A OR B) = 0.61, and P(A AND B) = 0.19, find P(B).
Answers
Answer:
0.41
Step-by-step explanation:
p (A) = 0.2
P (B) =?
P (A or B) = 0.61
but P (A or B) = P (A) + P (B)
therefore P(B) = P (A or B) - P(B)
= 0.61 - 0.2
= 0.41
