I need help right now plz

Answer:

1. A

2. B

3. B

Step-by-step explanation:

1. 180+57-94= 29

2. 4x + 7 + 97 + 180 - 17x - 13 = 180

-13x = -91

x = 7

3. 180 - 64-38 = 78

180-78 =. 102

Answer:

A) 29°

B) 7°

B) 102°

Step-by-step explanation:

1. ------------------------

2.  ------------------------

3.  ------------------------

Y=mx+b is the slope intercept form so to rearrange that equation it would be y=⅔x-⁵/3

It is represented in symbolic notation as :

1 + 2x2+ 2x - 8 = 80

The sphere with diameter PQ is given by equation (1-1)+(x+4)2 + (x + 2)2 = 80, where P = (1,1, -3) and Q = (1,9,1). You may use any form of numbers in the equation.

The sphere with diameter PQ has radius 5, volume 7pi and cuts a ball of radius 7 at point A. Find its equation if it is described by a parametric curve given by x-axis: (1-1)+(x+4)2 + (x + 2)2 = 80; y-axis: 4+(-2)*(x+3)2 = -3; z-axis: (x + 5)(x + 6)(x+7)=0.

(1-1)+(x+4)2 + (x+2)2 = 80. The value for x is 4, so we can say PQ=4x1. Now 4 times 1 will be 4, so that is The diameter of sphere with radius 0.

1 + 2x2+ 2x - 8 = 80.

For more such questions on equation of sphere:

https://brainly.com/question/20534134

#SPJ11

The 90% confidence interval for the population proportion of tenth graders reading at or below the eighth-grade level is (0.179, 0.220).

Firstly, determine the sample proportion:
The number of students reading at or below the eighth-grade level = Total students sampled - Students reading above the eighth-grade level

The number of students reading at or below the eighth-grade level = 1042 - 834

The number of students reading at or below the eighth-grade level= 208 students.
Sample proportion (p) = 208/1042

p = 0.1996 (rounded to four decimal places).

Now, we will determine the standard error (SE) for the sample proportion:
SE = √(p * (1 - p) / n)

= √(0.1996 * (1 - 0.1996) / 1042)

≈ 0.0124 (rounded to four decimal places)

Now, determine the z-score corresponding to the 90% confidence interval:
Since it is a 90% confidence interval, we will look for the z-score that has 0.05 in each tail (1 - 0.90 = 0.10, and 0.10 / 2 = 0.05). The z-score for a 90% confidence interval is 1.645.

Now, calculating the margin of error (ME):
ME = z-score * SE

= 1.645 * 0.0124 ≈ 0.0204 (rounded to four decimal places)

Lastly, constructing the 90% confidence interval:
Lower limit = p - ME

= 0.1996 - 0.0204

= 0.179 (rounded to three decimal places)
Upper limit = p + ME

= 0.1996 + 0.0204

= 0.220 (rounded to three decimal places)

So, the 90% confidence interval for the population proportion of tenth graders reading at or below the eighth-grade level is (0.179, 0.220).

Learn more about the confidence interval:

https://brainly.com/question/17212516

#SPJ11

Answer:

\(d = 3h - 6\)

Step-by-step explanation:

Step 1:  Solve for d

I am assuming that you are asking for me to solve for the variable d.  Let me know if what I am doing is not what you want.

\(h = \frac{d}{3} + 2\)

\(h - 2 = \frac{d}{3} + 2 - 2\)

\((h - 2) * 3 = \frac{d}{3} * 3\)

\(3h - 6 = d\)

Answer:  \(d = 3h - 6\)

A matrix is symmetric if it is equal to its transpose. Thus, a 3x3 matrix A is symmetric if and only if A = A^T, where A^T is the transpose of A.To determine the dimension of Sym(3), we simply count the number of basis vectors, which is 6. Therefore, dim[Sym(3)] = 6

Let's consider the set of all 3x3 symmetric matrices, denoted Sym(3). To find a basis for Sym(3), we can use the fact that a symmetric matrix has only 6 independent entries: the entries on the diagonal, and the entries above the diagonal (or below the diagonal, since the matrix is symmetric).

To construct a basis for Sym(3), we can consider the following matrices:

The matrix E_11, whose (1,1) entry is 1 and all other entries are 0.

The matrix E_12 = E_21, whose (1,2) and (2,1) entries are 1 and all other entries are 0.

The matrix E_13 = E_31, whose (1,3) and (3,1) entries are 1 and all other entries are 0.

The matrix E_22, whose (2,2) entry is 1 and all other entries are 0.

The matrix E_23 = E_32, whose (2,3) and (3,2) entries are 1 and all other entries are 0.

The matrix E_33, whose (3,3) entry is 1 and all other entries are 0.

It can be shown that any symmetric 3x3 matrix can be written as a linear combination of these matrices. Thus, they form a basis for Sym(3).

To determine the dimension of Sym(3), we simply count the number of basis vectors, which is 6. Therefore, dim[Sym(3)] = 6

Visit here to learn more about  matrix :  https://brainly.com/question/29132693
#SPJ11

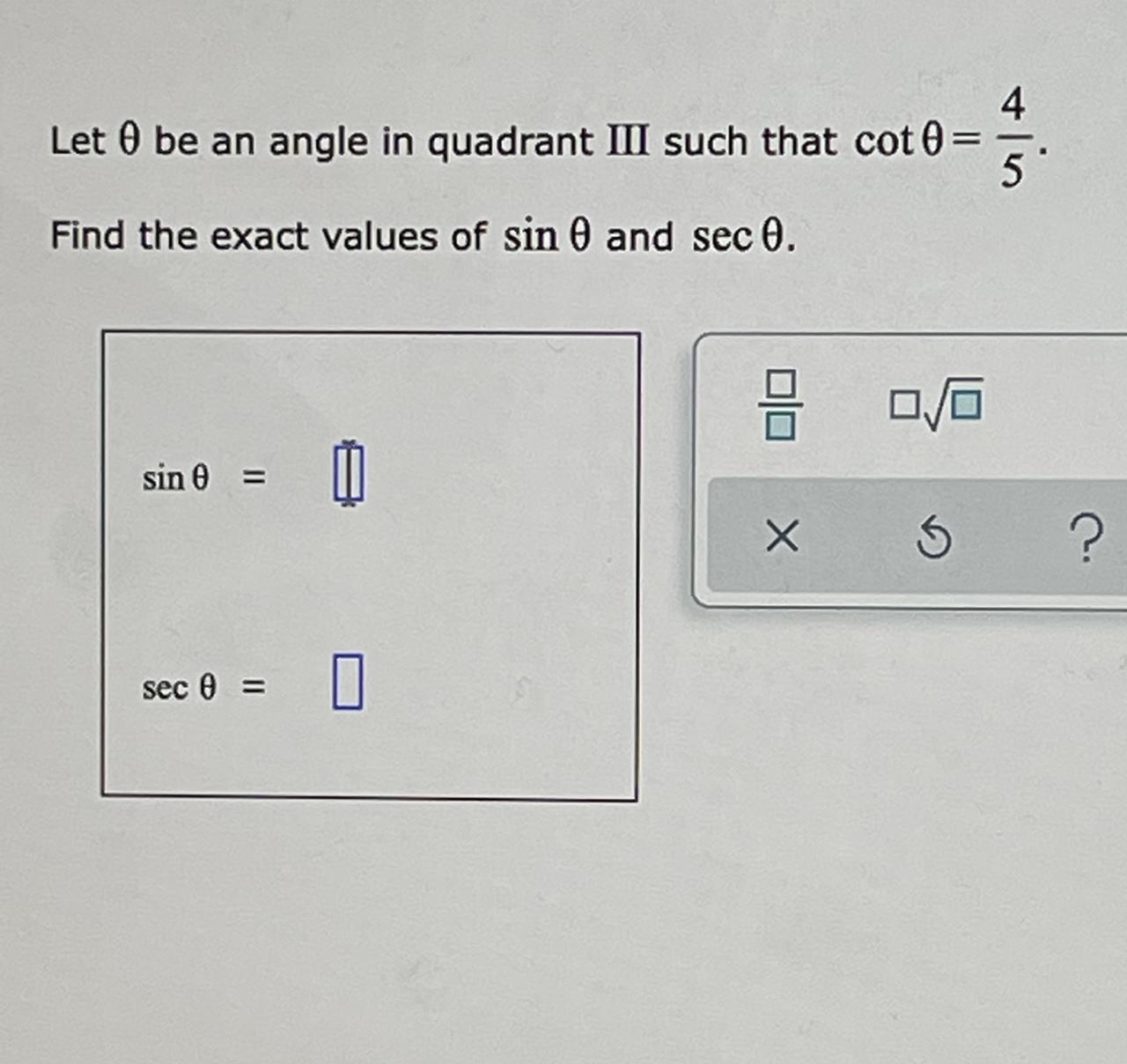
Answer:

see explanation

Step-by-step explanation:

Given

cotθ = \(\frac{4}{5}\) = \(\frac{adjacent}{opposite}\)

Use Pythagoras' identity to calculate the hypotenuse h

h² = 4² + 5² = 16 + 25 = 41 ( take square root of both sides )

h = \(\sqrt{41}\)

θ is in quadrant III where sinθ < 0 and secθ < 0

sinθ = \(\frac{opposite}{hypotenuse}\) = - \(\frac{5}{\sqrt{41} }\) = -  \(\frac{5\sqrt{41} }{41}\)

cosθ = \(\frac{adjacent}{hypotenuse}\) = - \(\frac{4}{\sqrt{41} }\)

secθ = \(\frac{1}{cos0}\) = - \(\frac{\sqrt{41} }{4}\)

9514 1404 393

Answer:

  a = (s +t)/(m +r)

Step-by-step explanation:

Add t, then divide by the coefficient of 'a'.

  \(a(m+r)-t=s \qquad\text{given}\\\\a(m+r)=s+t \qquad\text{add $t$}\\\\\boxed{a=\dfrac{s+t}{m+r}} \qquad\text{divide by $m+r$}\)

The cat population in Catonsville in 2007 was 200. The answer is option B.

Population refers to the total number of people, animals, or objects in a particular group or area. It is the entire group or collection of individuals, things, or events that we are interested in studying or describing.

We can use the given equation to find the cat population at any given time in years since the beginning of 2010. However, to find the population in 2007, we need to make a conversion from years since the beginning of 2010 to years since the beginning of 2007.

From the beginning of 2007 to the beginning of 2010, there are 3 years, so if we subtract 3 from the number of years since the beginning of 2010, we will get the number of years since the beginning of 2007. Therefore, we need to substitute t = -3 into the given equation and solve for p:

\(p = 1600(2)^t\\p = 1600(2)^(-3)\\p = 1600(1/8)\\p = 200\)

Therefore, the cat population in Catonsville in 2007 was 200. The answer is option B.

To know more about population visit:

https://brainly.com/question/27779235

#SPJ1

Step-by-step explanation:

50 th percentile means 50% are above and 50% are below.....this is the peak of the Bell Curve

Answer:

LOOK AT YOUR ANSWER IN PICTURE

Answer:

2nd one COA 40 140 90 130 50

Step-by-step explanation:

IF IM WRONG TELL ME AND I HELP YOU OUT AGAIN

Answer:

A=180 B=150 C=130 D=90 E= 60 F=40

Step-by-step explanation:

A=180 B=150 C=130 D=90 E= 60 F=40

Step-by-step Explanation :-

Hey there,

As per question,

\( \frac{24}{ \frac{(8 \times 3)}{4} \times 2} \times (15 - 4)\)

\( = > \frac{24}{ \frac{24}{2}} \times 11\)

\( = > 24 \times \frac{2}{24} \times 11\)

Now cancelling both 24's we get :

\( = > 2 \times 11\)

\( = > 22\)

Therefore, The answer is 22

《 For smaller step, check the attached image also》

~Benjemin360

Have a great day :)

The mass of the rectangular sheet of metal based on its dimensions can be found to be 0.00532 kg

First, find the area of the rectangular sheet of metal:

= Length x Width

= 15.7 x 12.9

= 202.53 cm²

The mass of the rectangular sheet of metal is 38.1g per cm² so the mass in grams is:
= 202.53 / 38.1

= 5.3157 grams

In kilograms this is:

= 5.3157 / 1,000

= 0.00532 kg

Find out more on mass in kg at https://brainly.com/question/355158

#SPJ1

Answer:

Suppose that we have two similar figures.

Then if a given side of one of the figures has a measure M, the correspondent side in the other figure has a measure M' = k*M

Where k is the scale factor.

Then if the perimeter of the first figure is P, the perimeter of the other figure will be P' = k*P

And if the area of the first figure is A, then the area of the other figure will be:

A' = k^2*A

Then the quotient between the perimeters is:

P'/P = k

And the ratio between the areas is

A'/A = k^2

So what we need to do, is find the value k.

In the image, we can see that the base of the larger figure is 30 yd, and the base of the smaller figure is 12 yd.

If we define the smaller figure as the original one, then we will have:

M = 12 yd

M' = 30 yd

M' = 30yd = k*12yd = k*M

Solving for k we get:

k = 30yd/12yd = 2.5

Then the ratio between the perimeters is:

P'/P = k = 2.5

And the ratio of the area of the larger figure (A') to the smaller figure (A) is:

A'/A = k^2 = (2.5)^2 = 6.25

Given that AC is a diameter of the circle, we can conclude that triangle ABC is a right triangle, with AC being the hypotenuse. The area of the circle is not directly related to finding the lengths of BC or AB, so we will focus on the given information: AB = 16 units.

Using the Pythagorean theorem, we can find BC. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (AC) is equal to the sum of the squares of the other two sides (AB and BC):

AC² = AB² + BC²

Substituting the given values, we have:

(AC)² = (AB)² + (BC)²

(AC)² = 16² + (BC)²

(AC)² = 256 + (BC)²

Now, we need to find the length of AC. Since AC is a diameter of the circle, the length of AC is equal to twice the radius of the circle.

AC = 2 * radius

To find the radius, we can use the formula for the area of a circle:

Area = π * radius²

Given that the area of the circle is 2897 units², we can solve for the radius:

2897 = π * radius²

radius² = 2897 / π

radius = √(2897 / π)

Now we have the length of AC, which is equal to twice the radius. We can substitute this value into the equation:

(2 * radius)² = 256 + (BC)²

4 * radius² = 256 + (BC)²

Substituting the value of radius, we have:

4 * (√(2897 / π))² = 256 + (BC)²

4 * (2897 / π) = 256 + (BC)²

Simplifying the equation gives:

(4 * 2897) / π = 256 + (BC)²

BC² = (4 * 2897) / π - 256

Now we can solve for BC by taking the square root of both sides:

BC = √((4 * 2897) / π - 256)

To find the measure of angle BC (mBC), we know that triangle ABC is a right triangle, so angle B will be 90 degrees.

In summary:

BC = √((4 * 2897) / π - 256)

mBC = 90 degrees

for similar questions on area of the circle.

https://brainly.com/question/14068861

#SPJ8

Answer:

x= 2, y=4 hope this helps

Step-by-step explanation:

The coordinates of A' and C' will not be the same. The perimeter and area of ΔA'B'C' will be the same. The measure of ∠B' and the slope of A'C' will be the same.

Transformation is rearranging a graph by a given rule it could be either increment of coordinate or decrement or reflection.

If we reflect any graph about y = x then the coordinate will interchange it that (x,y) → (y,x).

As per the given translation,

2 units down and 3 units right

The coordinate will change as,(x,y) → (x+3,y-2) so it will change.

The transformation consists only of linear transformation no rotation exists thus area and perimeter will remain the same.

The slope and angle are unchanged irrespective of any transformation.

Hence "A' and C' will not have the same coordinates. The boundaries and surface area of ΔA'B'C' will be identical. The slope of A'C' and the measure of ∠B will be equal.".

To learn more about the transformation of graphs,

brainly.com/question/3099136

#SPJ1

Answer:

0 divided by 0 is undefined.

Any fraction when has a zero in the numerator will give a decimal value of zero only.

-TheUnknownScientist 72

The volume of the pyramid is 9 cubic inches

The volume of the prism is 85.5 cubic inches

The volume of the monument replica is 94.5 cubic inches

Given,

The replica of a monument consist of;

Rectangular prism and square pyramid.

Length of the rectangular prism = 3 inches

Width of the rectangular prism = 3 inches

Height of the rectangular prism = 9.5 inches

Base of the square pyramid = 3 x 3 inches

Height of the square pyramid = 3 inches

We have to find the volume of rectangular prism, square pyramid and the monument replica;

V = 3 x 3 x 9.5 = 85.5 cubic inches

V = 3 x 3 x (3/3) = 3 x 3 x 1 = 9 cubic inches

Therefore,

The volume of the pyramid is 9 cubic inches

The volume of the prism is 85.5 cubic inches

The volume of the monument replica is 94.5 cubic inches

Learn more about pyramid and prism here;

https://brainly.com/question/11336446

#SPJ1

Answer: 6 over 1, 12 over 2, 18 over 3, and 24 over 4

Step-by-step explanation:

hope this helps!

(Sorry if wrong)

Domain of the radical function of the form f(x) = √(ax + b) + c is given by the solution of the inequality ax + b ≥ 0 and the range is the all possible values obtained by substituting the domain values in the function.

We know that the general form of a radical function is,

f(x) = √(ax + b) + c

The domain is the possible values of x for which the function f(x) is defined.

And in the other hand the range of the function is all possible values of the functions.

Here for radical function the function is defined in real field if and only if the polynomial under radical component is positive or equal to 0. Because if this is less than 0 then the radical component of the function gives a complex quantity.

ax + b ≥ 0

x ≥ - b/a

So the domain of the function is all possible real numbers which are greater than -b/a.

And range is the values which we can obtain by putting the domain values.

To know more about radical function here

https://brainly.com/question/29086604

#SPJ4

To find g(-2), we'll substitute -2 for x in the equation g(x) = -4x² - 5x + 9. So,g(-2) = -4(-2)² - 5(-2) + 9g(-2). The value of g(-2) is -6.

To find g(-2), substitute -2 for x in the equation

g(x) = -4x² - 5x + 9 to get

g(-2) = -6 + 9g(-2)

We are given three functions as follows:

f(x) = (1/3)x - 5, g(x)

= -4x² - 5x + 9, and

h(x) = 1/(x - 8) + 3.

We are asked to find g(-2), which is the value of g(x) when x = -2.

Substituting -2 for x in the equation g(x) = -4x² - 5x + 9, we get

g(-2) = -4(-2)² - 5(-2) + 9.

This simplifies to g(-2) = -16 + 10 + 9 = -6.

Hence, g(-2) = -6.

The value of g(-2) is -6.

To know more about substitute visit:

brainly.com/question/29383142

#SPJ11

Answer:

x = 11

z = 86

Step-by-step explanation:

8x + 6 and 10x-16 are vertical angles

Vertical angles are pairs of angles that are opposite each other and have the same vertex, or point of intersection. They are formed when two lines intersect at a point, and are always congruent, or of equal measure.

To solve this equation, we need to isolate the variable x on one side of the equation. To do this, we can start by subtracting 6 from both sides of the equation:

8x + 6 - 6 = 10x - 16 - 6

8x = 10x - 22

Now we can subtract 8x from both sides of the equation:

8x - 8x = 10x - 22 - 8x

0 = 2x - 22

To solve for x, we can add 22 to both sides of the equation:

0 + 22 = 2x - 22 + 22

22 = 2x

Finally, we can divide both sides of the equation by 2 to find the value of x: 22 / 2 = 2x / 2

x = 11

Therefore, the solution to the equation is x = 11.

Now that we have x, z is a supplementary angle to 8x + 6 (or you could do 10x - 16)

Supplementary angles are pairs of angles that add up to 180 degrees. They are formed when two lines intersect at a point, and the angles formed at the intersection are supplementary.

First plug in x, 8x + 6 = 8(11) + 6 = 88 + 6 = 94

180 - 94 = z

z = 86

Answer:

Company B would be the best place to get their supply from. First, I multiplied all of the quantities by 5 (33.72*5)(44.48*5)(42.6*5) and got my sums. Then, I subtracted the price to be earned from selling the plush toys by the price of the bundle. Lastly, I compared the amounts earned by using each.

A. $26.28 B. $35.52 C. $32.4

Company B is the best place to buy from.

Answer:

B) (2,0) and (0,-4)

Step-by-step explanation:

The answer to the system of equations is where the two intersect on the graph, in this case on the points (2,0) and (0,-4)

The shape of the normal distribution is bell shape and it is also symmetrical from the left and right sides about the origins (mean).

What is a normal distribution?

A normal distribution is a function on some random variables, which represent the set of all those random variables in a symmetrical bell shape about the mean value.

It shows that the probability of occurrence of some data which is distributed over a function is more at or around the mean.

It is also known as probability distribution curve.

The normal distribution has two parameters:

What is the shape of the normal distribution?

The normal distribution curve is at it's peak at the mean value. This shows that the probability of occurrence of the data or value is more concentrated or distributed about the mean. It is also symmetric about the mean. As we more further from the mean, we see that the normal distribution curve gradually decreases showing that the probability of occurrence of the data or the values decreases. The shape that this curve forms is like a bell-shaped. So the shape of normal distribution is bell shape.

Hence, the shape of the normal distribution is bell shape and it is also symmetrical from the left and right sides about the origins (mean).

Know more about "normal distribution" here: https://brainly.com/question/15103234

#SPJ4

For every 100 free throws Chris Paul attempted, he made approximately 93 of them.

We have,

Chris Paul's free throw percentage of 93.4 means that he made 93.4% of his free throw attempts during the 2020-21 season.

In other words, for every 100 free throws he attempted, he made approximately 93 of them.

This is a high free throw percentage and indicates that Chris Paul is a skilled free throw shooter.

Thus,

For every 100 free throws Chris Paul attempted, he made approximately 93 of them.

Learn more about percentages here:

https://brainly.com/question/11403063

#SPJ1

The probability that exactly one component meets specifications can be found by taking the product of the probabilities. Therefore, P(X = 1) ≈ 0.0019 (rounded to five decimal places).

The probability that a component meets specifications is given by: P(meets specifications) = p

Now, let X be the number of components that meet specifications. Since there are three mechanical components, X can take the values 0, 1, 2 or 3. Now, we need to determine P(X = 1).

The probability that exactly one component meets specifications can be found by taking the product of the probabilities that one component meets specifications and the other two do not meet specifications.

P(X = 1) = P(One component meets specifications)

= P(meets specifications) × P(does not meet specifications) × P(does not meet specifications) + P(does not meet specifications) × P(meets specifications) × P(does not meet specifications) + P(does not meet specifications) × P(does not meet specifications) × P(meets specifications) = p(1 − p)(1 − p) + (1 − p)p(1 − p) + (1 − p)(1 − p)p

= 3p(1 − p)2 = 3(0.95)(0.02)2 ≈ 0.0019

Therefore, P(X = 1) ≈ 0.0019 (rounded to five decimal places).

The above calculation shows that there is only a small probability that exactly one component will meet specifications.

Learn more about probability here:

https://brainly.com/question/29062095

#SPJ11

The difference quotient is equal to -3a2h, which simplifies to -3a2 divided by h.  This is the slope of the line tangent to the graph of f(x) = -x3 at the point (a, -a3).

The difference quotient is a way to approximate the slope of the line tangent to the graph of a given function. To calculate the difference quotient for f(x) = -x3, we can use the formula f(a h) − f(a) h. Plugging in values for f(a) and f(a h), we get -a3 - (-(a+h)3) / h. We can simplify this expression by multiplying out the parentheses: -a3 + (a3 + 3a2h + 3ah2 + h3) / h. We can then combine like terms and cancel out the h's to get -3a2h / h, which simplifies to -3a2 / h. This is the difference quotient for f(x) = -x3 at the point (a, -a3).

Learn more about quotient here

https://brainly.com/question/16134410

#SPJ4