Answers
Answer:
For a triangle to be equiangular all its three interior angles must be equal, that is, each angle should measure 60˚.
Step-by-step explanation:
Related Questions
The lateral surface area of a cube is 400cm². Its total surface area is
_______
a)600cm² b) 2400cm² c) 500cm² d) 650cm²
Answers
Answer:
Step-by-step explanation:
Lateral surface area of cube = 4a²
4a² = 400
a² = 400÷4
a² = 100
a = √100 = √10*10
a = 10 cm
Total surface area = 6a²
= 6 * 10²
= 6* 100
= 600 cm²
Answer:
A
Step-by-step explanation:
I believe that I did this before.
what is the simpllified form of the expression x+x+10+2x-16
Answers
Answer:
4x-6
Step-by-step explanation:
x+x+10+2x-16
Combine like terms
x+x+2x +10-16
4x -6
4x-6
Answer:
\(4x - 6\)
Step-by-step explanation:
\(x + x + 10 + 2x - 16\)
combine like terms
\(x + x + 2x + 10 - 16 \\ 2x + 2x - 6 \\ = 4x - 6\)
hope this helps
brainliest appreciated
good luck! have a nice day!
write and solve a real world problem in which you find the commission
Answers
A car salesman earns a 3% commission on sales. If he sells a car for $27,990, how much commission will he earn?
($27,990)*(0.03) = $839.70
The Jones family will pay their insurance broker a commission of $1,750.00.
Commission is an amount of money paid to an employee or company as an incentive to sell more. A straight commission is a percentage of sales.
To know more about Commission
Refer this link:
https://brainly.com/question/957886
#SPJ1
. What is 112,252
rounded to the nearest ten thousand?
Answers
Answer:
110,000
Step-by-step explanation:
Provide numerical measures of individuals. The values of a quantitative variable can be added or subtracted and provide meaningful results?
Answers
Quantitative variables provide numerical measures that can be added/subtracted with meaningful results.
Discrete variables are quantitative and have a finite or countable number of positive values.
Continuous variables are quantitative and have an infinite number of possible values that are not countable and also measure with some sort of scale that uses numbers.
Qualitative variables allow for the classification of individuals based on some attribute or characteristic and also provide numerical measures of individuals.
Arithmetic operations such as addition and subtraction can be performed on the values of a quantitative variable and will provide meaningful results.
To know more about Quantitative variables:
https://brainly.com/question/14037311
#SPJ4
Which of the following is a solution of this equation?
A.
(5,0)
B.
(-1, 1)
C.
(3,-1)
D.
(-2,-3)

Answers
Answer:
D. (-2,-3)
Step-by-step explanation:
substitute the point values of \(x\) and \(y\) into the equation \(y=\frac{1}{2}x-2\)
A. \(0=\frac{1}{2}(5)-2\)
\(0=2.5-2\)
\(0\) ≠ \(0.5\)
B. \(1=\frac{1}{2}(-1)-2\)
\(1=-.5-2\)
\(1\) ≠ \(-2.5\)
C. \(-1=\frac{1}{2}(3)-2\)
\(-1=1.5-2\)
\(-1\) ≠ \(-0.5\)
D. \(-3=\frac{1}{2}(-2)-2\)
\(-3=-1-2\)
\(-3=-3\)
A radio transmission tower is 160 feet tall. How long should a guy wire be if it is to be attached 13 feet from the top and is to make an angle of 29\deg with the ground? Give your answer to the nearest tenth of a foot.
Answers
x = 147 / 0.5446 ≈ 270.2 ft
To find the length of the guy wire for a radio transmission tower, trigonometry concepts are applied. Given a tower height of 160 feet, with the wire attached 13 feet from the top and making an angle of 29° with the ground, we can solve for the length of the guy wire, represented by x.
Using the Pythagorean theorem and considering the right triangle formed by the tower height, the wire attachment point, and the ground, we can set up the equation:
x = √((160 - 13)² + x²)
Next, we apply the tangent function to the given angle:
tan(29°) = (160 - 13) / x
Simplifying, we have:
0.5446 = 147 / x
To solve for x, we rearrange the equation:
x = 147 / 0.5446 ≈ 270.2 ft
Rounding to the nearest tenth of a foot, the length of the guy wire required is approximately 270.2 feet. This wire is attached 13 feet from the top of the tower and makes a 29° angle with the ground.
Trigonometry plays a crucial role in solving real-world problems involving angles and distances. It provides a mathematical framework for calculating unknown values based on known information, enabling accurate measurements and constructions.
Learn more about the applications of trigonometry in real-world scenarios:
https://brainly.com/question/31340190
#SPJ11
A guy is throwing pumpkins off a five story (15 meters high) building and wants the messiest result possible (highest velocity impact).
a) He first throws a pumpkin downward at 45 degrees below the horizon at 15 m/s. How fast does the pumpkin hit the ground? At what angle does it hit?
b) He then throws a second pumpkin upward with the same velocity 45 degrees above the horizon. How fast does the second pumpkin hit the ground?
c) Which strategy (throwing the pumpkin up or down) results in a higher velocity impact? Think about why this might be.
Answers
a) The pumpkin thrown downward from a five-story building (15 meters high) results in the messiest impact (highest velocity impact).
b) The second pumpkin will hit the ground at the same velocity as the first pumpkin, regardless of the direction of throw.
c) Throwing the pumpkin downwards results in a higher velocity impact because the gravitational force of the Earth adds to the initial velocity.
The velocity of the pumpkin is directly proportional to the height of the building from where it is thrown. Thus, the pumpkin thrown from a five-story building has a higher velocity than that thrown from a shorter building. To get the messiest impact, the pumpkin must be thrown downward, and not upward. This is because the gravitational force of the Earth adds to the initial velocity, making the pumpkin hit the ground with a higher velocity. The velocity at which the second pumpkin hits the ground will be the same, regardless of the direction of throw. This is because the initial velocity of the pumpkin is the same in both cases, and the force of gravity acting on it is also the same.
Know more about gravitational force here:
https://brainly.com/question/29190673
#SPJ11
Given secant of theta is equal to the square root of 6 over 2 comma what is cos?
Answers
The value of cos θ is equal to 1/3 when sec θ= √6/2.
Since we are given the value of secant of theta, we can use the relationship between secant and cosine to find the value of cosine of theta.
Let's start by recalling the definitions of secant and cosine functions. The secant of an angle is defined as the reciprocal of the cosine of that angle.
In other words, secθ = 1/cosθ
Conversely, the cosine of an angle is defined as the reciprocal of the secant of that angle.
cosθ = 1/secθ
We are given that secθ= √6/2
We can use this value to find cosθ= 1/secθ
cosθ = 1 / (√6/2)
To simplify this expression, we can multiply both the numerator and denominator by 2/sqrt(6).
cosθ = ((2/√6) / (√6/2) * (2/√6))
cosθ = (2/√6) / 1
cosθ = (2/√6 * √6/√6)
cosθ = 2/6 = 1/3
Therefore, the value of cosθ is equal to 1/3 when secθ = sqrt(6)/2.
For more such questions on cos θ visit:
https://brainly.com/question/21867305
#SPJ8
HELPPPPP
7 8 ÷ 1 4
A) 3 1 2
B) 4
C) 7 16
D) 7 32
Answers
Answer:
A) 3 1/2
Explanation:
\(\hookrightarrow \sf \dfrac{7}{8} \div \dfrac{1}{4}\)
rewrite the following
\(\hookrightarrow \sf \dfrac{7}{8} * \dfrac{4}{1}\)
join both fractions
\(\hookrightarrow \sf \dfrac{7*4}{8}\)
multiply
\(\hookrightarrow \sf \dfrac{28}{8}\)
simplify the following
\(\hookrightarrow \sf \dfrac{7}{2}\)
turn into mixed fraction
\(\hookrightarrow \sf 3\dfrac{1}{2}\)
Answer:
\(\dfrac{7}{2}\)
Step-by-step explanation:
Given expression:
\(\dfrac{7}{8} \div \dfrac{1}{4}\)
Simplify the expression:
\(\implies \dfrac{7}{8} \div \dfrac{1}{4}\)
\(\implies \dfrac{7 \div 1}{8 \div 4}\)
\(\implies \dfrac{7}{2}\)
A square region with perimeter 60 inches is made with square inch tiles. Bob removes one tile from the square and rearranges the remaining tiles without any overlap to make a rectangular region with minimum perimeter. How many inches are in the perimeter
Answers
Answer:
60 inches
Step-by-step explanation:
The perimeter will be minimized when the tiles are rearranged to form a rectangle with dimensions as close to each other as possible.
Rectangle dimensionsThe square has a side length of ...
P = 4s ⇒ s = P/4 . . . . . P is perimeter, s is side length
(60 in)/4 = 15 in . . . . length of the side of the square
The square has an area of ...
A = s²
A = (15 in)² = 225 in²
When 1 tile is removed, the resulting area, in square inches, is ...
A = 225 -1 = 15² -1² = (15 -1)(15 +1) = 14×16
PerimeterThe perimeter of a rectangle is given by ...
P = 2(L+W)
For this rectangle, the perimeter is ...
P = 2(14 in + 16 in) = 2(30 in) = 60 in
The perimeter of the rectangle is 60 inches.
What is the perimeter of a square with side length (2x-3)?
Answers
Answer:
Perimeter = 8x - 12
Step-by-step explanation:
The perimeter of a square is:
p = 4(side length)
on this case:
p = 4(2x-3)
p = 4*2x + 4*-3
p = 8x - 12
Solve for x: the quantity of x plus 16 all over 3 = 3x (1 point) a x = −7 b x = −13 c x = 8 d x = 2
Answers
Answer:
D. X=2
Step-by-step explanation:
Answer:
X=2
Step-by-step explanation:
Please help need by tomorrow it would be very very very appreciated

Answers
The solution of the given system of equations is (8, -1). of the given system of equations is (8, -1).
One method to solve the given system of equations is substitution:
- Solve one of the equations for one of the variables (e.g., x = 9 + y from the second equation).
- Substitute the expression for the variable into the other equation.
- Solve the resulting equation for the remaining variable.
- Substitute the value for the remaining variable back into one of the original equations to find the value of the other variable
Using this method with the given equations
- x - y = 9 -> x = 9 + y
- 3x + 2y = 22 -> 3(9 + y) + 2y = 22
- Simplifying and solving for y: 27 + 5y = 22 -> 5y = -5 -> y = -1
- Substituting y = -1 into x = 9 + y: x = 8
To check this solution, we can substitute these values back into both original equations and confirm that they are true statements.
For such more questions on solution
https://brainly.com/question/24644930
#SPJ8
150,000 fans are expected to attend a football game. Fifty-two percent of them will not be able to park at the stadium, so satellite parking will be used. Thirty buses will shuttle fans from the satellite parking areas. Each bus can carry 65 fans. How many trips will each bus have to make to get everyone to the stadium?
A. 39
B. 40
C. 38
D. 41
Answers
The correct option is B. The trips will each bus has to make to get everyone to the stadium is 40 trips.
The number of fans who will need to use satellite parking is:
150,000 x 0.52 = 78,000
Each bus can carry 65 fans, so the total number of trips required is:
78,000 / 65 = 1200
Therefore, each bus will need to make 1200/30 = 40 trips
Satellite parking typically offers lower rates than the central parking area and provides a shuttle service to transport passengers to and from the main terminal. This type of parking is a popular option for travelers who need to park their car for an extended period of time, such as those going on vacation or business trips.
Satellite parking can be located either on-site or off-site, depending on the transportation hub. Some airports have several satellite parking lots located at various distances from the main terminal, while others have a single satellite parking area. Overall, satellite parking is an important component of transportation infrastructure, as it provides a convenient and affordable parking solution for travelers while also helping to alleviate congestion in the main parking area.
To learn more about Satellite parking visit here:
brainly.com/question/24882579
#SPJ4
find the eigenvalues λ1<λ2 and associated unit eigenvectors u⃗ 1,u⃗ 2 of the symmetric matrix
Answers
To find the eigenvalues (λ1, λ2) and associated unit eigenvectors (u⃗ 1, u⃗ 2) of a symmetric matrix, further details about the specific matrix are required. The process involves solving the characteristic equation associated with the matrix and finding the corresponding eigenvectors through eigende composition.
Given a symmetric matrix, the eigenvalues (λ1, λ2) can be found by solving the characteristic equation det(A - λI) = 0, where A is the matrix, λ represents the eigenvalue, and I is the identity matrix. By solving this equation, we obtain the eigenvalues.
Once the eigenvalues are determined, we can find the associated eigenvectors (u⃗ 1, u⃗ 2) by solving the system of equations (A - λI)u⃗ = 0, where A is the matrix, λ is an eigenvalue, and u⃗ is the eigenvector. The unit eigenvectors are obtained by normalizing the eigenvectors to have a length of 1.
The specific process of finding the eigenvalues and eigenvectors of a symmetric matrix depends on the matrix itself. Therefore, without the matrix's explicit representation or values, it is not possible to provide the exact eigenvalues and eigenvectors.
Learn more about system of equations here:
https://brainly.com/question/20067450
#SPJ11
In ΔMNO, the measure of ∠O=90°, MO = 24, NM = 25, and ON = 7. What ratio represents the cosecant of ∠N?
Answers
Answer:
\csc N = \frac{\text{hypotenuse}}{\text{opposite}}=\mathbf{\frac{25}{24}}
cscN= opposite
hypotenuse = 24/25
Step-by-step explanation:
drag and drop each number to its correct position on the number line -3/8, 7/8, -2 1/2, 2 1/2
I NEED HELPP FASTTT
Answers
Answer: -4 1/3, -1/6, 5/6, 4 1/3
Step-by-step explanation:
To the left of the number line we would have the negatives which are -4 1/3, and -1/6. Then, to the right we have 5/6 and 4 1/3 because they are positives. That's the order they would go in from left to right on the number line.
Answer:
In order of least to greatest:
-2 1/2, -3/8, 7/8, 2 1/2
Step-by-step explanation:
First, we look at the negatives. Which one is the bigger number -2 1/2 or -3/8?
-3/8 is the bigger number, making the negative order on the left -2 1/2, -3/8.
Now we look at the positives. Which one is bigger, 7/8 or 2 1/2? 2 1/2 is the bigger number. Meaning the right side of the number line should look like 7/8, 2 1/2.
All together we get -2 1/2, -3/8, 7/8, 2 1/2
x=6y-7 (show work)
4x+y=-3
Answers
The value of the variables are x = -1 and y = 1
What is a simultaneous equation?Simultaneous equations are described simply as two or more algebraic equations having the same unknown variables and for which the same value of the variables satisfies all the equations.
From the information given, we have the simultaneous equations;
x=6y-7
4x+y=-3
Now, substitute the value of the variable x in equation 2, we have;
4(6y - 7) + y = -3
expand the bracket, we get;
24y - 28 + y = -3
collect the like terms, we have;
24y + y = -3 + 28
add the values
25y = 25
Make 'y' the subject
y = 1
Then, x = 6(1) - 7 = 6 - 7 = -1
Learn about simultaneous equations at: https://brainly.com/question/16863577
#SPJ1
i’m losing brain cells

Answers
Answer:
14. Reflection
15. A
16. D
Step-by-step explanation:
A reflection creates a mirror image of the original figure because if you think of a mirror, you think of your or an object's reflection.
For number 15, the image is unclear so I will just tell you how to do it. When it says translate 6 units right, and 3 units up, you would need to move every point to the next line, at the right side 6 times. Then, you move every point to the top 3 times and plot your new points.
Number 16 is also unclear, so as many numbers it takes you to get to the x-axis, that is the amount you will move the point away from the exact point on the x-axis. For instance, it takes point C 1 unit to get to the x-axis, so we will plot it 1 point into the x-axis. At the end of this, you should see the image like the pre-image. So it will look like a mirror.
Kari has $400 in a savings account the interest rate is 10% compounded annually which type of model best fits this situation
Answers
Answer:
What model?
Step-by-step explanation:
the probability of a manufacturing defect in an aluminum beverage can is .00004. if 100,200 cans are produced, find the following probabilities. (this is binomial distribution)
Answers
In a manufacturing process where the probability of a defect in an aluminum beverage can is 0.00004, we are interested in finding the probabilities associated with producing a certain number of defective cans out of a total of 100,200 cans.
In this scenario, we can use the binomial distribution to calculate the probabilities. The binomial distribution is used to model situations where there are a fixed number of independent trials (can production) with two possible outcomes (defective or non-defective).
Let's denote X as the random variable representing the number of defective cans. The probability mass function of the binomial distribution is given by:
P(X = k) = C(n, k) * p^k * (1 - p)^(n - k)
where n is the total number of cans produced, p is the probability of a defective can, and C(n, k) is the binomial coefficient.
a) To find the probability of exactly x defective cans, substitute the values into the formula mentioned above: P(X = x) = C(100200, x) * (0.00004)^x * (1 - 0.00004)^(100200 - x).
b) To find the probability of at most x defective cans, we need to calculate the cumulative probability: P(X ≤ x) = P(X = 0) + P(X = 1) + ... + P(X = x).
c) To find the probability of more than x defective cans, we can subtract the cumulative probability from 1: P(X > x) = 1 - P(X ≤ x).
By plugging in the appropriate values and performing the calculations, we can determine the desired probabilities associated with producing a certain number of defective cans out of 100,200 cans.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
Consider a situation in which P(X) = and P(Y) = . If P(X and Y) is = , which best describes the events? They are independent because P(X) · P(Y) = P(X and Y). They are independent because P(X) + P(Y) = P(X and Y). They are dependent because P(X) · P(Y) = P(X and Y). They are dependent because P(X) + P(Y) = P(X and Y). Mark this and re
Answers
They are dependent because P(X) · P(Y) = P(X and Y)
How to determine dependent events probabilities?
The statement "P(X) · P(Y) = P(X and Y)" is the formula for independent events. However, since P(X and Y) is not equal to the product of their individual probabilities, the events are thus dependent. In other words, the occurrence of event X affects the probability of event Y, and vice versa. Therefore, the events are not independent and must be analyzed as such when making predictions or decisions based on their outcomes.
Learn more about independent
brainly.com/question/30905572
#SPJ11
what is 125% of 12.8
Answers
The required value of the given percentage is 16. "125%" represents 125 parts out of 100, which is equivalent to 1.25 times the original value.
To find 125% of 12.8, we can multiply 12.8 by 1.25.
First, we convert the percentage to decimal form by dividing it by 100. So, 125% becomes 1.25.
Next, we multiply 12.8 by 1.25:
12.8 × 1.25 = 16.
Therefore, 125% of 12.8 is 16.
Multiplying 12.8 by 1.25 increases it by 25% or adds one-quarter of the original value. Thus, the result of 16 represents an increase of 25% from 12.8.
Thus, the required value of the given percentage is 16.
Learn more about percentages here:
brainly.com/question/24159063
#SPJ6
question 81 pts the effectiveness of two types of textbook is compared. a class of 30 students is randomly divided into two groups. one group uses digital textbooks and the other group uses paper textbooks. a summary of their test scores at the end of the session is given below. digital textbook: paper textbook: construct a 90% confidence interval for the difference in scores between the two groups assuming underlying normal distributions with equal variance. find the upper bound of the confidence interval (round off to first decimal place).
Answers
Therefore , the upper bound of the confidence interval is - 8.82 .
What is confidence interval ?A confidence interval in frequentist statistics is a range of estimates for an unobserved parameter. The most common confidence level for computing confidence intervals is 95%, however other levels, including 90% or 99%, are sporadically employed.
Here,
n1 = 17 ; X1' = 78.4 ; s1² = 90.3
n2 = 13 ; X2' = 92 ; s2² = 107.8
Confidence interval :
(x1 - x2) ± Tcritical * \(\sqrt{[(sp^{2} /n1 + sp^{2}/n2)]}\)
Pooled variance = Sp²
=> Sp² = (df1*s1² + df2*s2²) / (n1 + n2 - 2)
df = n - 1
Sp² = (16*90.3 + 12*107.8) / 28
Sp² = 97.8
Tcritical, 90%, df = n1 + n2 - 2 = 28 (1 - tail)
Tcritical = 1.313
(78.4-92)±1.313*sqrt[(sp²/n1 + sp²/n2)]
Margin of Error = Tcritical *\(\sqrt{[(sp^{2} /n1 + sp^{2}/n2)]}\)
Margin of Error = (1.313 * √(97.8/17 + 97.8/13)) = 4.7771473
Upper boundary :
(78.4-92) + 4.7771473
-13.6 + 4.7771473
= -8.8228527
= - 8.82
Therefore , the upper bound of the confidence interval is - 8.82 .
To know more about confidence interval , visit
brainly.com/question/24131141
#SPJ4
Circle a has a radius of 17 inches. what is the circumference of circle a?
Answers
Answer:
106,81 inch ..............
The formulae for the circumference is 2*pi*r
Meaning 2 X 17 which is 32 and 32 X pi is 32*pi
At your school, SAT scores are normally distributed with a mean of 1550 and a standard deviation of 310. If you randomly select a person who has taken the SAT, what is the probability that they scored between a 1300 and a 1500?
Answers
The probability that they scored between a 1300 and a 1500 is 0.261086299693
What is probability?The probability is the measure of the likelihood of an event to happen. It measures the certainty of the event.
Given that, mean (μ) = 1550
Standard deviation (σ) = 310
z-score = x-μ/σ
The probability that they scored between a 1300 and a 1500 =
P(1300<x<1500) = P(1300-1550/310 < x < 1550-1500/310)
= P(-0.8<x<0.16)
= P(z<0.16) - P(z<-0.8)
= 0.261086299693
Hence, the probability that they scored between a 1300 and a 1500 is 0.261086299693
Learn more about probability, click;
https://brainly.com/question/30034780
#SPJ1
3. Solve 3(x - 2) = 27. A. 21 B 9.67 D.7
Answers
Answer:
x = 11
Step-by-step explanation:
Distribute the 3
3x-6=27
Add 6
3x=33
Divide 3
X=11
I need help ASAP!!! 40points!!!

Answers
Answer: rfthhhhh
Step-by-step explanation:
Answer:
what
Step-by-step explanation:
HELP MEEEEE PLEASEEEE
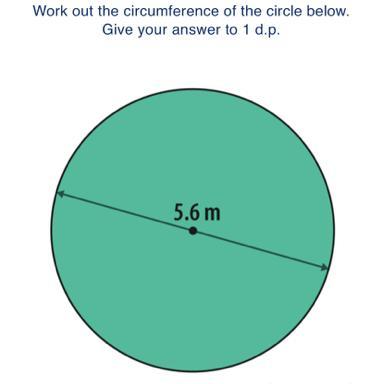
Answers

