How would you get the variable alone in the equation s ÷ 10 = 12? A. Multiply both sides of the equation by 10. B. Multiply both sides of the equation by 12. C. Divide both sides of the equation by 10. D. Divide both sides of the equation by 12.
Answers
A. Multiply both sides of the equation by 10.
SInce 10 is being divided with s, weneed to isolate it. To do this multiply 10 on both sides.
Related Questions
5(x-2) +25=0 5x - 10x +25=0 -5r+ 25 = 0 -5x+25 – 25 = 0 – 25 −5r=–25 –5x –25 -5 -5 x=5
Answers
ZA and ZB are supplementary angles. If mA = (2x − 9)º and m
ZB = (2x +21)°, then find the measure of ZA.
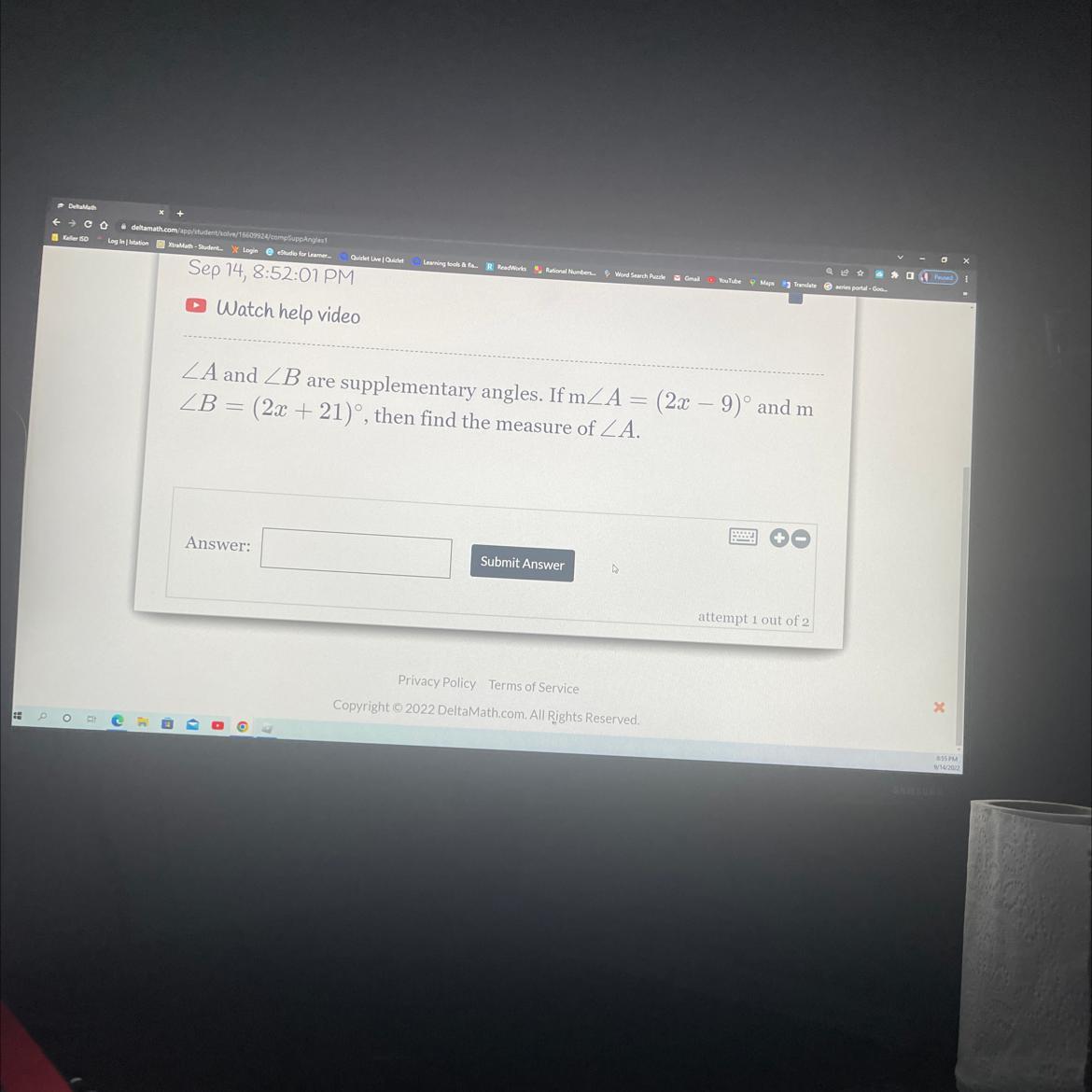
Answers
angle A = 30
(2x-9) = (2x+21)
+9 +9
2x=2x+30
-2x -2x
=30
You deposit $200 in a savings account that pays a simple interest rate of 4.5% per year. How much interest will you earn after 7 years?
Answers
Answer:
$63.00
Step-by-step explanation:
$200.00× 0.045=9
9×7=63
6.12 it is 9:00 p.m. the time until joe receives his next text message has an exponential distribution with mean 5 minutes. (a) find the probability that he will not receive a text in the next 10 minutes. (b) find the probability that the next text arrives between 9:07 and 9:10 p.m. (c) find the probability that a text arrives before 9:03 p.m. (d) a text has not arrived for 5 minutes. find the probability that none will arrive for 7 minutes.
Answers
So the probability that Joe will not receive a text in the next 10 minutes is approximately 0.865. So the probability that the next text arrives between 9:07 and 9:10 p.m. is approximately 0.149. So the probability that a text arrives before 9:03 p.m. is approximately 0.393. So the probability that no text will arrive for 7 minutes, given that no text has arrived for 5 minutes, is approximately 0.394.
(a) To find the probability that Joe will not receive a text in the next 10 minutes, we can use the cumulative distribution function (CDF) of the exponential distribution. The CDF gives the probability that the time until the next text is less than or equal to a given time t. The CDF of an exponential distribution with mean 5 minutes is:
\(F(t) = 1 - e^{(-t/5)}\)
To find the probability that Joe will not receive a text in the next 10 minutes, we need to find F(10):
\(F(10) = 1 - e^{(-10/5)}\)
\(= 1 - e^{(-2)}\)
≈ 0.865
(b) To find the probability that the next text arrives between 9:07 and 9:10 p.m., we need to find the probability that the time until the next text is between 7 and 10 minutes. We can use the CDF again to find this probability:
P(7 < X < 10) = F(10) - F(7)
\(= (1 - e^{(-10/5)}) - (1 - e^{(-7/5)})\)
\(= e^{(-7/5)} - e^{(-2)}\)
≈ 0.149
(c) To find the probability that a text arrives before 9:03 p.m., we need to find the probability that the time until the next text is less than 3 minutes. We can use the CDF again to find this probability:
P(X < 3) = F(3)
\(= 1 - e^{(-3/5)}\)
≈ 0.393
(d) To find the probability that no text will arrive for 7 minutes, given that no text has arrived for 5 minutes, we can use the memoryless property of the exponential distribution. The memoryless property states that the conditional distribution of the time until the next text, given that no text has arrived in the first 5 minutes, is the same as the original distribution. In other words, the fact that no text has arrived in the first 5 minutes does not affect the probability of a text arriving in the next 7 minutes.
Therefore, the probability that no text will arrive for 7 minutes, given that no text has arrived for 5 minutes, is the same as the probability that no text will arrive for 7 minutes starting from scratch. This is the probability that the time until the next text is greater than 7 minutes. Using the CDF of the exponential distribution, we can calculate:
P(X > 7) = 1 - F(7)
\(= 1 - (1 - e^{(-7/5)})\)
= \(e^{(-7/5)}\)
≈ 0.394
To know more about probability,
https://brainly.com/question/30034780
#SPJ11
Find (g∘k)(1)for g(x)=11x2−4x+6and k(x)=4x−11. (g∘k)(1)=
Answers
The first step you have to follow is to find k(1) by replacing each x in k(x) for 1:
\(k(1)=4(1)-11=4-11=-7\)Now, find g(k(1)), it means, g(-7):
\(g(-7)=11(-7)^2-4(-7)+6=573\)(g°k)(1)=573.
MC) Determine the surface area of the cylinder. (Use π = 3.14) net of a cylinder where radius of base is labeled 5 inches and a rectangle with a height labeled 4 inches
Pls help it’s for 20 point pls
Answers
The surface area of the cylinder is 314.6 square inches.
The surface area of a cylinder is given by the formula:
S.A. = 2πrh + 2πr²
Where r is the radius of the circular base of the cylinder and h is the height of the cylinder.
If we know the radius and height of a cylinder, we can easily calculate its surface area.
To solve for the surface area of the cylinder whose radius is 5 inches, we use the formula and substitute the values. The net of a cylinder whose radius of the base is labeled 5 inches and a rectangle with a height labeled 4 inches is given below:
Given the radius, r = 5 inches, height of cylinder, h = 4 inches.
Substituting the values in the formula:
S.A. = 2πrh + 2πr²
= 2 × 3.14 × 5 × 4 + 2 × 3.14 × 5²
= 157.6 + 157
= 314.6 square inches
For more related questions on surface area:
https://brainly.com/question/2835293
#SPJ8
Solve two thirds times v plus 6 equals one third times v minus 2.
v equals negative eight thirds
v equals eight thirds
v = −24
v = 24
Answers
The value of v using the equation ( 2v/3 ) + 6 = ( v/3 ) - 2 is v = - 24.
Two-thirds of anything is an amount that is two out of three equal parts of it. Similarly, one-third of something is an amount that is one out of three equal parts of it.
Now, we have
Two-thirds times v plus 6 equals one-third times v minus 2.
Hence, when the above statement is expressed as an equation we get:
Two third of v + 6 = one third of v - 2
2/3 × v + 6 = 1/3 × v - 2
( 2v/3 ) + 6 = ( v/3 ) - 2
Adding 2 on both sides of the equation,
( 2v/3 ) + 6 + 2 = ( v/3 ) - 2 + 2
( 2v/3 ) + 8 = ( v/3 )
Subtracting 2v/3 from both sides of the equation,
2v/3 + 8 - 2v/3 = v/3 - 2v/3
8 = ( v - 2v )/3
- v/3 = 8/1
By cross multiplication,
- v × 1 = 8 × 3
- v = 24
Multiplying each side by - 1,
v = - 24
Learn more about equations here:
https://brainly.com/question/2972832
#SPJ1
If 30% of a number is 600, what is 65% of the number?
Include all steps and explain how answer was
found.
Answers
65% of the number is 1300.
To find 65% of a number, we can use the concept of proportionality.
Given that 30% of a number is 600, we can set up a proportion to find the whole number:
30% = 600
65% = ?
Let's solve for the whole number:
(30/100) * x = 600
Dividing both sides by 30/100 (or multiplying by the reciprocal):
x = 600 / (30/100)
x = 600 * (100/30)
x = 2000
So, the whole number is 2000.
Now, to find 65% of the number, we multiply the whole number by 65/100:
65% of 2000 = (65/100) * 2000
Calculating the result:
65/100 * 2000 = 0.65 * 2000 = 1300
learn more about proportion
https://brainly.com/question/31548894
#SPJ11
Pls help algebra 1
A clerk earns $125 per day, plus a commission equal to
10% of her sales, s. The clerk earns less than $180 on
Monday
Enter an inequality that represents all possible values for
the clerk's sales, s, on Monday.
Answers
Answer:
0.1s + 125 < 180
The weight of 4 eggs is 180g. Identify the constant of the proportionality of total weight to number of eggs.
Answers
Answer: 13.6 grams per egg.
Step-by-step explanation:
Part A: Write an algebraic expression for 6 more than 7 times a number. (5 points)
Part B: Write a verbal expression for 3(n + 8). (5 points)
Answers
The algebraic expression of the part A is 6+7x. And the verbal expression for 3*(n+8) is "the triple of the sum between the numbers n and 8".
Linear ExpressionA linear expression can be represented by a line. The standard form for this equation is: y=ax+b , for example, y=2x+7.
Part AFirst, you should choose a variable for unknow number. Here, the variable will be x. Then, 7 times a number can be represented for 7x.
The word more will be represented for the add symbol (+). Thus,
the algebraic expression is 6+7x.
Part BThe expression 3*(n+8) can be represented for the sentence:
The triple of the sum between the numbers n and 8.
Learn more about the algebraic expression here:
https://brainly.com/question/2164351
#SPJ1
I need someone to explain this to me because I don’t understand this.

Answers
Answer:
In the expression 250(1/2)^t/4, the following meanings can be attributed to the numbers:
250: This is the initial amount of caffeine in milligrams present in the coffee when it was brewed.
(1/2): This is the decay factor or the rate at which the caffeine content decreases over time. In other words, it represents the fraction of caffeine that remains after each hour. Here, the expression (1/2)^t means that the caffeine content will decrease by a factor of 1/2 after each hour.
t: This represents the time elapsed in hours since the coffee was brewed.
4: This is a scaling factor or a unit conversion factor used to convert the expression into milligrams. The expression 250(1/2)^t/4 represents the amount of caffeine remaining in milligrams after t hours.
To summarize, the expression 250(1/2)^t/4 models the amount of caffeine remaining in a coffee after t hours, where 250 is the initial amount of caffeine in milligrams, (1/2) is the decay factor or the fraction of caffeine that remains after each hour, t is the time elapsed in hours, and 4 is the scaling factor used to convert the expression into milligrams.
Among the answer choices provided, the second one is the most accurate:
250 represents the amount of caffeine in a body. 1/2 represents the decay rate of the caffeine. 4 represents the amount of hours it takes for the caffeine to reach its half-life.
The given expression 250(1/2)^t/4 models the amount of caffeine remaining in a coffee after t hours, where 250 is the initial amount of caffeine in milligrams, (1/2) is the decay factor or the fraction of caffeine that remains after each hour, t is the time elapsed in hours, and 4 is the scaling factor used to convert the expression into milligrams. Therefore, the answer choices that mention coffee consumption or growth factor of coffee are not correct in this context.
In this expression, the fraction 1/2 represents the decay rate or the fraction of caffeine that remains after each hour. The number 4 is used to scale the expression into milligrams and does not represent the half-life of caffeine. The half-life of caffeine is the amount of time it takes for half of the initial caffeine amount to decay, and it can be calculated using the formula t1/2 = ln(2) / k, where k is the decay constant.
HELP I'LL GIVE YOU 69 BRAINLY POINTS

Answers
Answer:
The value of sin 270 degrees is -1.
Step-by-step explanation:
Using trigonometric identities, we know, sin(270°) = cos(90° - 270°) = cos(-180°).
Write an algebraic expression that models the situation "You had 250 minutes left on your cell phone, and you talk an hour a week." Use w to represent the number of weeks. A. 250 + 60w B. 250 minus left parenthesis 7 right parenthesis left parenthesis 60 right parenthesis w C. 250 minus 60w D. 250 + 7w
Answers
Answer:
C. 250-60w
Step-by-step explanation:
Express each of the following sums in summation notation and then com- pute where possible. Let X take the values 1-4, 2-2, x3 = 0,4 4, 54 and Y take the values y₁ = -1, 92=-0.5, 93 = 0, y4 1,35 = 1.5. =
(a) 1+ 2+ 3+ 4+ X5
(b) y2 y3+ YA
Answers
The sum in summation notation of the expression (a) 1 + 2 + 3 + 4 + X5, where X takes the values 1-4, is ΣX from 1 to 4. In other words, it represents the summation of X over the range 1 to 4.
In summation notation, the expression (a) 1 + 2 + 3 + 4 + X5 can be written as ΣX, where X takes the values from 1 to 4. The capital sigma (Σ) represents the summation operator, and the variable X is summed over the range 1 to 4. This means that we need to substitute X with each value from 1 to 4 and add them together.
When we evaluate the expression, we have:
ΣX = 1 + 2 + 3 + 4 = 10
However, the expression also includes X5, indicating that X takes the value 5 as well. Therefore, we add 5 to the sum:
ΣX = 10 + 5 = 15
So, the sum of 1 + 2 + 3 + 4 + X5, where X takes the values 1-4, is equal to 15.
Moving on to expression (b) y2 + y3 + Y, where Y takes the values y₁ = -1, y₂ = -0.5, y₃ = 0, y₄ = 1.35, we can express it in summation notation as ΣY from 1 to 3. This represents the summation of Y over the range 1 to 3.
Since Y has a different value for each term, we simply substitute Y with each value from 1 to 3 and add them together:
ΣY = y₁ + y₂ + y₃ = -1 + (-0.5) + 0 = -1.5
Hence, the sum of y₂ + y₃ + Y, where Y takes the values y₁ = -1, y₂ = -0.5, y₃ = 0, y₄ = 1.35, is equal to -1.5.
Learn more about summation notation here:
https://brainly.com/question/11764646
#SPJ11
Can someone help me

Answers
In a highway vehicles are passing according to a Poisson process having a rate of 300 per hour. Suppose each vehicle is a car with probability 86% and at truck with probability 14%. (a) Determine the distribution of the number of cars in the highway during a two hour period. (b) Determine the expected number of cars that will pass the highway before the first truck.
Answers
The distribution of the number of cars on the highway during two hours follows a binomial distribution with parameters n=2 and p=0.86, and the expected number of cars that will pass the highway before the first truck is approximately 1.16 cars.
(a) The distribution of the number of cars on the highway during two hours follows a Poisson distribution with a rate of 300 cars per hour. Since each vehicle is a car with a probability of 86%, we can use the binomial distribution to determine the probability of a specific number of cars in the two hours. The probability mass function of the number of cars, denoted by X, can be calculated as \(P(X = k) = (2Ck) * (0.86)^k * (0.14)^2^-^k\), where k ranges from 0 to 2. This gives us the probability distribution of the number of cars in the two hours.
(b) To determine the expected number of cars that will pass the highway before the first truck, we can utilize the geometric distribution. The probability of a car passing the highway before the first truck is 86%. Therefore, the expected number of cars, denoted by Y, can be calculated as \(E(Y) = 1 / 0.86 = 1.16\) cars. This means that on average, approximately 1.16 cars will pass the highway before the first truck.
To learn more about Binomial distribution, visit:
https://brainly.com/question/29137961
#SPJ11
In training for a swim meet, Logan swam 750 meters in of an hour. His swimming partner, Mila, swam of Logan's distance in of an hour.
Fill in the blanks to compare Mila's and Logan’s swimming speeds.
Compare Mila's and Logan’s swimming speeds. Show your work.
Answers
Is this your question?
In training for a swim meet, Logan swam 750 meters in 1/3 of an hour. His swimming partner, Mila, swam 2/3 of Logan's distance in 1/4 of an hour. (the question is What is Mila's average swimming speed?)
Answer:
Mila's average swimming speed is 34.44 m/min.
Logan's average speed is 2.25 kilometers per hour.
Step-by-step explanation:
Given:
In training for a swim meet, Logan swam 750 meters in 1/3 of an hour.
His swimming partner, Mila, swam 2/3 of Logan's
To Find:
What is Logan's average swimming Speed?
Solution:
The relationship between speed, distance, and time is easily remembered when you consider that speed is written in terms of units of distance per units of time. (miles per hour, or kilometers per hour, for example) "per" means "divided by".
\(\left[Speed=\frac{Distance}{Time} \right]\)
\(\left[speed = (750 m)/(1/3 h) = 2250 m/h = 2.25 km/h\right]\)
Logan's average speed is 2.25 kilometers per hour.
-------------------------------------------------------------------------------------------------------------
Given:
In training for a swim meet, Logan swam 750 meters in 1/3 of an hour.
His swimming partner, Mila, swam 2/3 of Logan's distance in 1/4 of an hour
To find:
What is Mila's average swimming speed?
Solution:
The distance swam by Logan = 750 m
The distance swam by Mila = 2/3 of Logan's distance = 2/3 x 750 = 2 x 250 = 500
The time taken by Mila to swim 500 m = 1/4 of an hour = 1/4 x 60 = 15 Minutes [since 1 hr = 60 mins]
We know the formula as:
\(\left[Speed=\frac{Distance}{Time} \right]\)
Now, substituting the values in the formula above to find the speed of swimming of Mila,
The average swimming speed of Mila = \(\frac{500m}{15mintues}\)\(=33.34m/min\)
Therefore, Mila's average swimming speed is → 34.44 m/min.
Work out x. Give reasons for your answer.

Answers
Answer:
The measurement for x is 80°
Step-by-step explanation:
In the picture, we see two parallel lines cut by a transversal line. Since the lines are cut by a transversal, then there are a few things we should know that can help us find the value of x.
Corresponding angles are congruent. Angles that are right beside each other (such as ∠CBD and ∠CBA) are a linear pair. This means that they have a total measurement of 180° when added together.Now that we know these things, we can use this information to find the measurement of ∠CBA. We do this by subtracting 100 from 180 because ∠CBA and ∠CBD are a linear pair. Once we know the measurement of this angle, then it will be much easier to find the value of x.
180 - 100 = 80
So, the measurement of ∠CBA is 80°. Now, ∠CBA and ∠x are corresponding angles so this means that they have the same measurements. If the measurement of ∠CBA is 80°, then the measurement of ∠x is also 80°
x = 80°
what does the slope of the regression line tell us
Answers
The slope of a regression line provides valuable insights into the relationship between two variables in a linear regression analysis. It represents the rate of change in the dependent variable for a one-unit increase in the independent variable.
Specifically, a positive slope indicates that as the independent variable increases, the dependent variable also tends to increase. Conversely, a negative slope suggests an inverse relationship where an increase in the independent variable corresponds to a decrease in the dependent variable.
The magnitude of the slope is crucial as it quantifies the strength of the relationship. A larger slope signifies a steeper incline or decline, indicating a stronger association between the variables. Additionally, the slope can be interpreted as the predicted change in the dependent variable when the independent variable increases by one unit, assuming all other variables remain constant.
Overall, the slope of the regression line serves as a crucial indicator of the direction, strength, and magnitude of the relationship between variables in a linear regression model.
To know more about regression line, refer here:
https://brainly.com/question/29753986#
#SPJ11
Find the area of the shaded region.
80⁰
5 cm
A≈ [?] cm²
Enter a decimal rounded to the nearest tenth.
![Find the area of the shaded region.805 cmA [?] cmEnter a decimal rounded to the nearest tenth.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/VZj6v3MgeTAYfJlSu8vTquJVna84LbKY.png)
Answers
The area of the shaded region for the circle is derived to be equal to 73.4 square centimeters.
How to evaluate for the area of shaded regionThe shaded region is the segment area in the circle, so it is derived by subtracting the area of the segment from the area of the circle as follows:
area of the circle = 22/7 × 5 cm × 5 cm
area of the circle = 78.57 cm²
area of sector = 80/360 × 22/7 × 5 cm × 5 cm
area of sector = 17.46 cm²
area of triangle = 5 cm × sin40° × 5 cm × cos40°
area of triangle = 12.31 cm²
area of the segment = 17.46 cm² - 12.31 cm²
area of the segment = 5.15 cm²
area of the shaded region = 78.57 cm² - 5.15 cm²
area of the shaded region = 73.42 cm²
Therefore, the area of the shaded region for the circle is derived to be equal to 73.4 square centimeters.
Read more about area here:https://brainly.com/question/14137384
#SPJ1
I WILL MARK BRAINLIEST IF CORRECT!!
Home values are expected to decreased by 3% per year. Hadlee Recently purchased a home for $200,000. Which of the following equations can be used to represent the value of the home x years after the purchase?
A) f(x) = 200000(1.03)^x
B) f(x) = 200000(0.97)^c
C) f(x) = 3(1.03)^x
D) f(x) =3(0.97)^x
Answers
Answer:
B
Step-by-step explanation
Multiplying by 0.97 will decrease $200,000 to $194,000.
^c is x years after the purchase, so having (0.97)^c will make the $200,000 value decrease more and more.
The admission fee at the fair is $1.50 for children and $4 for adults. On a certain day, 2200 people enter the fair and $5050 is collected. How many children, c, and how many adults, a, attended?
Which system of equations can be used to solve the problem?
Responses
c + a = 2200
1.50c + 4a = 5050
, , c + a = 2200, , 1.50 c + 4 a = 5050,
c + a = 2200
1.50c + a = 5050
, , c + a = 2200, , 1.50 c + a = 5050,
c + 4a = 2200
1.50c + a = 5050
Answers
Answer:
c+a=2,200
1.50c+4c=5,050
Step-by-step explanation:
We know that on one day, 2,200 people entered the fair.
So, using the variables, c/a, we know that c+a=2,200
This gives us our first equation in this system of equations.
We are also given that a total of $5,050 was made. $1.50 is a children ticket/admission fee and $4 per adult.
So:
1.50c+4c=5,050
Thus our system of equations looks like:
c+a=2,200
1.50c+4c=5,050
Hope this helps! :)
an example of each respectfully..an NFA that is surjective, bijective, and injective.
Answers
1. An example of a surjective NFA (Non-deterministic Finite Automaton) is one where every state has at least one outgoing transition for every input symbol.
2. An example of a bijective NFA is one where every state has exactly one outgoing transition for every input symbol.
3. An example of an injective NFA is one where no two states have the same outgoing transition for any input symbol.
An NFA is a computational model used in theoretical computer science and automata theory to describe the behavior of finite state machines. In the context of surjective, bijective, and injective NFAs, we consider the properties of the transitions between states.
A surjective NFA is one in which every state has at least one outgoing transition for every input symbol. This means that for any input symbol, there is a valid transition from every state to some other state or states. An example of a surjective NFA could be a state machine representing a regular expression that matches any sequence of characters.
A bijective NFA is one in which every state has exactly one outgoing transition for every input symbol. In other words, for each input symbol, there is a unique and deterministic transition from every state to another state. An example of a bijective NFA could be a state machine representing a simple calculator that performs addition or subtraction.
An injective NFA is one in which no two states have the same outgoing transition for any input symbol. This means that for any input symbol, there is a unique transition from each state to another state. An example of an injective NFA could be a state machine representing a binary counter, where each state corresponds to a unique binary number.
These examples illustrate the different properties of surjectivity, bijectivity, and injectivity in NFAs and how they affect the transitions between states.
Learn more about Transition
brainly.com/question/14274301
#SPJ11
Could someone explain how they get Q from [T]beta ? This is Linear Algebra class: The change of coordinate matrix. Example 2 Let T be the linear operator on R2 defined by and let 3 and be the ordered bases in Example 1. The reader should verify that In Example 1, we saw that the change of coordilate matrix that changes 3'-coordinates into 3-coordinates is ?
Answers
We know that the transformation matrix Q transforms the 3-coordinates into 3'-coordinates, which is the inverse of the change of coordinate matrix that we obtained earlier.
The matrix of T with respect to the basis {(1, 1), (−1, 1)} for the domain and the basis {(1, 0), (0, 1)} for the codomain is [T]beta= [0 0 1 0], which is the change of coordinate matrix that changes 3'-coordinates into 3-coordinates.
Let T be the linear operator on R² defined by T(x, y) = (y, 0) and let {(1, 1), (−1, 1)} and {(1, 0), (0, 1)} be the ordered bases in Example 1.
The reader should verify that {T(1,1), T(−1,1)} = {(1,0), (0,0)} and {T(1,0), T(0,1)} = {(0,1), (0,0)}.
Hence, the matrix of T with respect to the basis {(1, 1), (−1, 1)} for the domain and the basis {(1, 0), (0, 1)} for the codomain is [T]beta= [0 0 1 0], which is the change of coordinate matrix that changes 3'-coordinates into 3-coordinates.
Thus, from the above explanation, we can get Q from [T]beta as follows:
Let Q be the transformation matrix that transforms the 3-coordinates into 3'-coordinates, which is nothing but the inverse of the change of coordinate matrix that we have obtained earlier.
So, Q = ([T]beta)^-1 = [(0, 0), (0, 0), (1, 0), (0, 1)].
Therefore, Q can be obtained from [T]beta as follows:
Q = ([T]beta)^-1 = [(0, 0), (0, 0), (1, 0), (0, 1)].
Thus, we get Q from [T]beta.
To know more about coordinates visit:
https://brainly.com/question/22261383
#SPJ11
hubble's original determination of galactic distances was a factor of 10 too small. assume that all of your galaxies were 10 times closer than they are, but that their radial velocities were unchanged. recalculate the age of the universe under these assumptions.
Answers
Hubble's original determination of galactic distances was a factor of 10 too small. Assuming that all of your galaxies were 10 times closer than they are, but that their radial velocities were unchanged, then the age of the universe under these assumptions is one-tenth of the previously calculated age.
To calculate the age of the universe using the given assumptions, we can make use of the Hubble's law, which relates the recessional velocity of galaxies to their distance:
v = H0 * d,
where:
- v is the recessional velocity of a galaxy,
- H0 is the Hubble constant (representing the present-day rate of expansion of the universe), and
- d is the distance to the galaxy.
If we assume that the galaxies were 10 times closer, we can rewrite the distance as d' = d/10.
Since the radial velocities are unchanged, we have v' = v.
Now, let's consider the inverse of the Hubble's law to calculate the time it took for galaxies to reach their current distances:
t = d/v.
Using the new values, we have:
t' = d'/v' = (d/10)/(v) = d/(10v).
However, we know that v = H0 * d, so substituting it in the equation:
t' = d/(10 * H0 * d).
The distance cancels out:
t' = 1/(10 * H0).
Therefore, if the galaxies were 10 times closer but had unchanged radial velocities, the age of the universe, denoted as t', is simply 1/10th of the original age of the universe, denoted as t:
t' = 1/10 * t.
Hence, the age of the universe under these assumptions is one-tenth of the previously calculated age.
To know more about Hubble's law refer here:
https://brainly.com/question/29869676#
#SPJ11
Find a Cartesian equation for the curve and identify it. r = 2 tan theta sec theta a. circle b. line c. parabola d. ellipse e. limacon
Answers
The Cartesian equation for the curve is y = 2x/(1+x^2), which is the equation of a limacon.'
The cartesian form of equation of a plane is ax + by + cz = d, where a, b, c are the direction ratios, and d is the distance of the plane from the origin.
To find the Cartesian equation for the curve, we need to use the relationships between polar and Cartesian coordinates:
x = r cos(theta) and y = r sin(theta)
Substituting r = 2 tan(theta) sec(theta), we get:
x = 2 tan(theta) sec(theta) cos(theta) = 2 sin(theta)
y = 2 tan(theta) sec(theta) sin(theta) = 2 tan(theta)
Know more about Cartesian equation here:
https://brainly.com/question/27927590
#SPJ11
In which interval does a root exist for this equation? tan(x) = 3x^2
PLEASE HELP

Answers
To determine the interval for which a root exists, you can use the intermediate value theorem.
First, observe that the left-hand side of the equation, tan(x), is undefined for x = (n + 1/2) π, where n is an integer. Thus, we can restrict our attention to the interval (-π/2, π/2) where the tangent function is continuous and strictly increasing.
Next, note that tan(0) = 0 and tan(π/6) = 1/√3 < 3/36 = 1/12. Also, as x approaches π/2 from the left, tan(x) approaches infinity, while 3x^2 approaches infinity faster. Therefore, there exists at least one root of the equation in the interval (0, π/6).
Similarly, tan(-π/6) = -1/√3 > -1/12, and as x approaches -π/2 from the right, tan(x) approaches negative infinity, while 3x^2 approaches infinity faster. Therefore, there exists at least one root of the equation in the interval (-π/6, 0).
Therefore, the equation tan(x) = 3x^2 has at least one root in the interval (-π/6, π/6).
Look at the triangles below.6BaiС4.321А-4-3-2-1 012.345B-1-2-3-419Point D will be added to the graph so thatAABC = AADC. What could be the coordinatesof point D?(1, -3)(2,-5)(3, -1)O (1, -2)


Answers
EXPLANATION
In order to get coordinates of D such that △ABC ≅ △ADC, the distance between the point A and the point D should be the same that the distance from the point A to the point B. Therefore, we just need to reflect the point B over the point A.
Reflecting the point B over the point A give us a point that is located 4 units right and 8 units down from the point B.
Thus, the coordinates of the point D are: (1,-3)

Consider the figure below. What would be the new coordinates of point P if the figure is translated (2, -3) and then reflected across the y-axis? A) P
Answers
Answer:
(2,3)
Step-by-step explanation: