How to solve this question without using calculator?
cos100+cos440
Answers
Answer:
0
Step-by-step explanation:
using the addition formula for cos
cos(a ± b ) = cosacosb ∓ sinasinb)
given
cos100 + cos440
= cos(180 - 80) + cos(360 + 80)
= cos180cos80 + sin180sin80 + cos360cos80 - sin360sin80
= (- 1)cos80 + 0(sin80) + (1)cos80 - 0(sin80)
= - cos80 + 0 + cos80 - 0
= 0
Related Questions
Which pair of figures is congruent?

Answers
Have a wonderful day, I hope this helped!
Determine whether each point could represent an x-intercept, y-intercept, both, or neither.A.(6,3)B.(-4,0)C.(18,0)D.(0,5)E.(0,0)
Answers
The y intercept is when the coordinate has the component of x equal to 0 and the x intercept is when y = 0 s
Please help me it’s due today

Answers
Answer:
C
Step-by-step explanation:
(6a - 2b) ^ 2
36a^2 + 2b^2
Solve by using the quadratic form
5r^2-8r+20=0
Answers
Answer:
Step-by-step explanation:

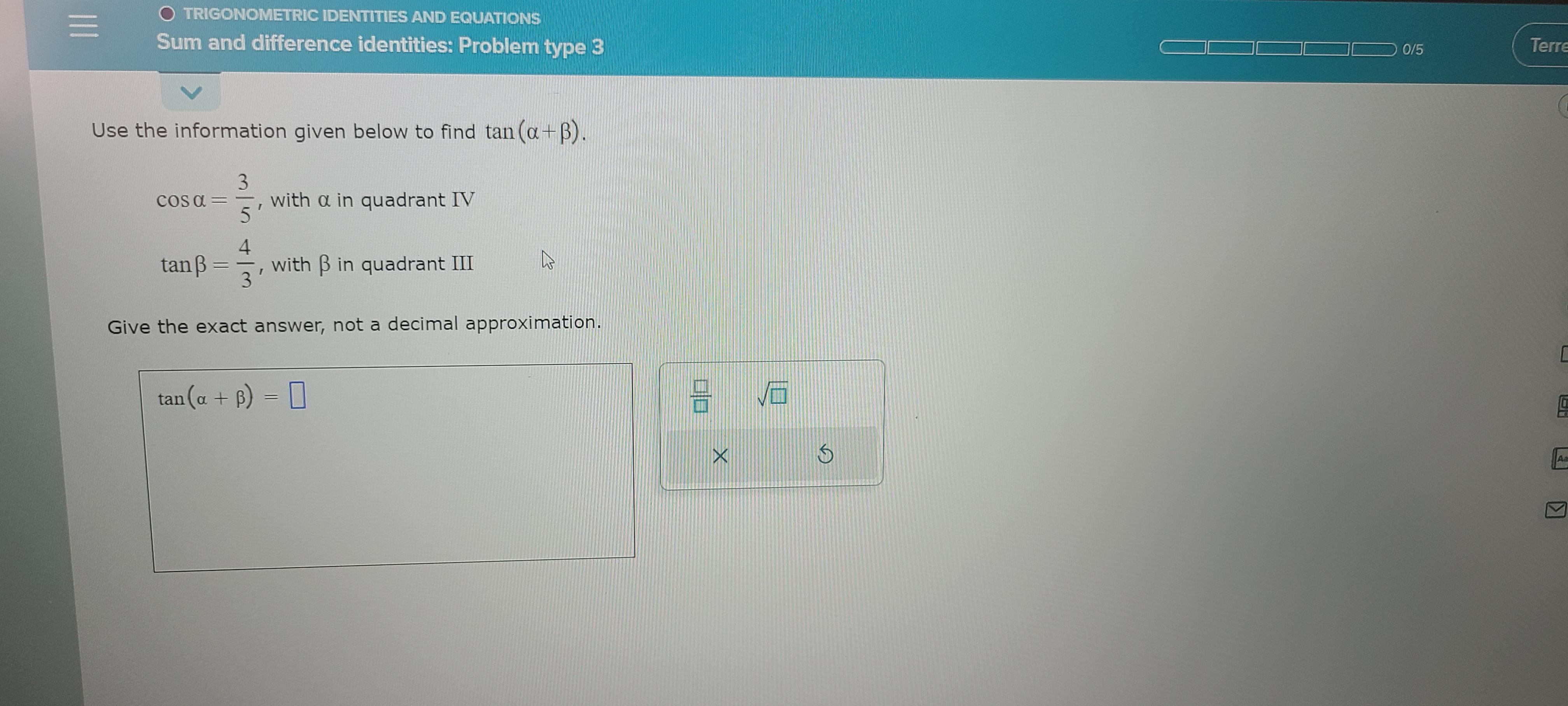
Use the information given below to find tan(a + B)
cos a = 3/5, with a in quadrant IV
tan B = 4/3, with B in quadrant I I I
Give the exact answer, not a decimal approximation.
tan(a + B) = ?
Answers
let's bear in mind that on the III Quadrant, sine and cosine are both negative, whilst on the IV Quadrant, sine is negative and cosine is positive, that said
\(\cos(\alpha )=\cfrac{\stackrel{adjacent}{3}}{\underset{hypotenuse}{5}}\hspace{5em}\textit{let's find the \underline{opposite side}} \\\\\\ \begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies o=\sqrt{c^2 - a^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{5}\\ a=\stackrel{adjacent}{3}\\ o=opposite \end{cases} \\\\\\ o=\pm \sqrt{ 5^2 - 3^2} \implies o=\pm \sqrt{ 16 }\implies o=\pm 4\implies \stackrel{IV~Quadrant }{o=-4} \\\\[-0.35em] ~\dotfill\)
\(\tan(\beta )=\cfrac{\stackrel{opposite}{4}}{\underset{adjacent}{3}}\implies \tan(\beta )=\cfrac{\stackrel{opposite}{-4}}{\underset{adjacent}{-3}} \\\\[-0.35em] ~\dotfill\\\\ \tan(\alpha + \beta) = \cfrac{\tan(\alpha)+ \tan(\beta)}{1- \tan(\alpha)\tan(\beta)} \\\\\\ \tan(\alpha + \beta)\implies \cfrac{ ~~\frac{-4}{3}~~ + ~~\frac{-4}{-3} ~~ }{1-\left( \frac{-4}{3} \right)\left( \frac{-4}{-3} \right)}\implies \cfrac{0}{1-\left( \frac{-4}{3} \right)\left( \frac{-4}{-3} \right)}\implies \text{\LARGE 0}\)
The number of hours needed to paint a house, h, varies inversely with the number of painters, n. Four painters need 6 hours to paint a house. Find the equation represents this relationship.
Answers
The equation that represents this relationship is h*n = 24.
How do we solve linear equations?
First order equations include all linear equations as a subset. In the coordinate system, lines are defined as having linear equations. A linear equation in one variable is made up of one homogeneous variable of degree one (i.e., only one variable). A linear equation could contain multiple variables. When a linear equation comprises two variables, for instance, linear equations in two variables are utilized. A mathematical statement known as an equation contains an algebraic expression and the equal symbol (=). It is the equation for a straight line. The equation is shown to be valid when values are substituted for the unknown values in the solutions of linear equations. When there is just one variable, there is just one answer.
Given, number of hours needed to paint a house = h
Number of painters needed to paint the house = n
Also, the relation between h and n is inverse, thus:
h*n = k, where k is the proportionality constant.
Therefore, initial equation derived is h*n = k --(i)
Putting h = 6 and n =4 in (i), we can get the value of k as
k = h*n = 6*4 = 24 --(ii)
Comparing (i) and (ii), we get,
h*n = 24, which is the required equation.
To learn more about linear equations tap on the link below:
https://brainly.com/question/2030026
#SPJ9
An accident investigator measured the skid marks of one of the vehicles involved in an accident. The length of the skid marks, d, was 117ft. Use the formula s=24d−−−√ to find s, the speed of the vehicle before the brakes were applied. Round your answer to the nearest tenth.
Answers
Answer:
The speed is 2808 ft/sStep-by-step explanation:
step one:
In this problem we are expected to substitute the value of d in the expression for velocity given as
\(s=24d\)
step two:
Given that
d= 117 ft
Substituting the value for d in the given equation we have
\(s= 24*117\\\\s=2808 ft/s\)
The problem basically tests our ability to perform basic substitution operation which we have performed, should you have any question or doubt, kindly respond to this question
Answer:
53
Step-by-step explanation:
(100 POINTS) How is constructing a perpendicular bisector similar to constructing a angle bisector? How is it different? PLEASE EXPLAIN IN FULL
Answers
Answer:
To construct a perpendicular bisector from a point on the line, think of the straight line as 180°, and you are bisecting that 180° angle.
The steps are the same as bisecting any given angle using only a straight edge and a compass.
Step-by-step explanation:
Mitzi received some gourmet brownies as a gift. The wrapper said each brownie was 420 calories, and had 113 calories of fat. What percent of the total calories in each brownie comes from fat?
Answers
The percent of the total calories in each brownie that comes from fat is 26.9%
What percent of the total calories in each brownie comes from fat?
We know that the total amount of calories in each brownie is 420 calories, so that number represents our 100%, then we can write the relation:
420 cal = 100%
Now, the fat has 113 calories, this is a percentage X that we want to find, so we can write:
113 cal = X
We have the two relations:
113 cal = X
420 cal = 100%
If we take the quotient we get:
(113 cal/420 cal) = X/100%
Solving for X.
(113 cal/420 cal)*100% = X = 26.9%
So, the percent of the total calories in each brownie that comes from fat is 26.9%.
If you want to learn more about percentages:
https://brainly.com/question/843074
#SPJ1
write the inequality shown -4x+y=-3
Answers
The inequality corresponding to the equation -4x + y = -3 is either y > 4x - 3 or y < 4x - 3, depending on the relationship between 4x - 3 and 0.
To write the inequality represented by the equation -4x + y = -3, we first need to manipulate the equation to express y in terms of x.
Starting with -4x + y = -3, we isolate y by adding 4x to both sides:
y = 4x - 3
Now we have y expressed in terms of x. To form the inequality, we consider the relationship between x and y. The inequality depends on whether the expression 4x - 3 is greater than or less than 0.
If 4x - 3 is greater than 0, then y is greater than 0, and we can write the inequality as:
y > 4x - 3
If 4x - 3 is less than 0, then y is less than 0, and we can write the inequality as:
y < 4x - 3
The inequality represents a region in the coordinate plane where the y-values are either greater than or less than the expression 4x - 3, depending on the direction of the inequality sign.
For example, if we choose a point (x, y) in the region above the line y = 4x - 3, where y is greater than 4x - 3, the inequality y > 4x - 3 will hold true. On the other hand, if we choose a point below the line, where y is less than 4x - 3, the inequality y < 4x - 3 will be satisfied.
For more such questions on inequality
https://brainly.com/question/30238989
#SPJ8
Mr. Jones has taken a survey of college students and found that 48 out of 64 students are liberal arts majors. If a college has 7693 students, what is the best estimate of the number of students who are liberal arts majors?
Answers
So
To find the best estimate of the number of students who are liberal arts majors, we could do the following:
Since we know that 48 out of 64 students are liberal arts majors and there are 7693 students, then:
\(\frac{48\cdot7693}{64}=5769.75\approx5770\)Therefore, 5770 students are liberal arts majors.
The number of students who are liberal arts majors is 5770.
There are 48 students out of 64 students are liberal arts majors.
This means:-
(48/64) × 100 = 75%
75% of total students are liberal arts majors.
Therefore,
The number of students in liberal arts majors = (75/100) × 7693
The number of students in liberal arts majors = 5769.75 ≈ 5770
Know more about Percentage at:-
https://brainly.com/question/17546886
Which is the last operation preformed when evaluating (8-2x)²+4 for x=3
A addition
B multiplication
C subtraction
D applying the exponent
Please hurry
Answers
Answer: I think its c sorry if im whrong
Hello all, what is 8y = 89.
Answers
Answer:
y= 11. 125
Step-by-step explanation:
8 y = 89
because you do not have another y on the other side simple divide
8 y = 89
89 / 8 = y
y= 11. 125
(Not sure what decimal place to round to so there are all 3 )
Hey there!
8y = 89
DIVIDE 8 to BOTH SIDES
8y/8 = 89/8
SIMPLIFY IT!
y = 89/8
y ≈ 11 1/8
y ≈ 11.125
Therefore, the answer is:
y = 89/8
Good luck on your assignment & enjoy your day!
~Amphitrite1040:)
y=9/4×2
sketch the graph of f and f on the same set of axes
Answers
The graph of the function \(f(x) = (9/4)x^2\) is a symmetric upward-opening parabola.
The graph represents a parabola that opens upward. As x increases, the corresponding y-values increase, forming a curved shape. The vertex of the parabola is at the origin (0,0). The graph is symmetric with respect to the y-axis, meaning that the left and right sides of the parabola are mirror images of each other.The slope of the graph gradually increases as x moves away from the origin. The steepness of the curve becomes more pronounced, indicating a faster rate of increase in y-values for larger x-values.The graph does not intersect the x-axis, indicating that there are no real roots or solutions for the equation f(x) = 0. The y-intercept of the graph is at (0, 0), and the y-values increase indefinitely as x approaches positive or negative infinity.Overall, the graph represents a quadratic function with a positive leading coefficient, resulting in an upward-opening parabolic curve. The graph has been attached.
For more questions on graph:
https://brainly.com/question/19040584
#SPJ8

Which equation is equivalent to this equation and written with the same base?
4x+1=16x−1
Answers
Answer:
\( 2^{2x + 2} = 2^{4x - 4} \)
Step-by-step explanation:
\( 4^{x + 1} = 16^{x - 1} \)
\( 2^{2(x + 1)} = 2^{4(x - 1)} \)
\( 2^{2x + 2} = 2^{4x - 4} \)
ANSWER ALL QUESTIONS
1. In a class of 28 pupils, 13 have pencils, 9 have erasers and 9 have neither pencils nor erasers. How
many pupils have both pencils and erasers?
2. A universal set, U consists of prime numbers with P and Q as subsets of U. If P and Q are given by
P = {n: 3(n + 1) = 2(n + 10)}, and Q = {n: 7<n<31}, list the elements of P n Q.
Answers
1. 3
29-9=19
13+9=22
22-19=3
I don't know number 2, sorry.
First evaluate the expression for the given value of the variable before combining like terms. Then, start over, and combine like terms first, and then evaluate the expression for the given value of the variable. Compare your results.
5x+3x; x=4
Answers
The answer before and after combining the like terms is 32.
How to evaluate the expression using the value of the variable given
Given: 5x+3x; x=4
To evaluate the expression before combining like terms. We substitute x = 4 into the expression the way it is:
5x + 3x = 5(4) + 3(4)
= 20 + 12 = 32
To evaluate the expression by combining like terms. We will add the like terms and then put x = 4 afterward:
5x + 3x = 8x
Put x = 4: 8x = 8(4) = 32
Since the expression evaluates to 32 before and after combining the like terms. Therefore, the results before and after the combination are the same.
Learn more about combining like terms on:
https://brainly.com/question/15203350
#SPJ1
what is the solution of this system of linear equations? 3y=3/2x+6 and 1/2y-1/4x=3
Answers
System Linear equation has no solution , because it is paralell lines but no intersection.
What is system linear equation?
An equation for a line is known as a linear equation. alternatively, y + 0.5x 3.5 = 0 and others. (Note that each linear equation is the same.) When multiple linear equations interact, we get a system of linear equations.
Here the given system linear equations,
\(3y=\frac{3}{2}x+6\) -------> 1 and \(\frac{1}{2}y-\frac{1}{4}x=3\) --------> 2
Divide by 3 of equation 1 on both sides then,
\(y=\frac{1}{2}x+2\) -----------> 3
Now put 3 into 2 then,
=> \(\frac{1}{4}x+1-\frac{1}{4}x=3\)
=> 1=3
Hence the given system equation has no solution , because it is paralell lines but no intersection.
To learn more about system linear equation
https://brainly.com/question/25858757
#SPJ1
What will happen to the measures of central tendency if the outlier is removed
Answers
What is the length of BC?

Answers
Answer: BC = 24
Step-by-step explanation:
Given:
AB = x+33
AC = 3x - 15
BC = x
<B = <C
Solution:
Because <B = <C, you can say the corresponding sides AB and AC are equal as well
AB = AC
x + 33 = 3x -15
48 = 2x
x = 24
Since x = BC
BC = x
BC = 24
Which pile of laundry has more shirts?
Pile 1
Three pants two shirts
Pile 2
Two shirts 4 pants
Answers
Answer:111
Step-by-step explanation:
1111
Name the relationship between ∠a and ∠b.

Answers
Answer:
B. Adjacent
Step-by-step explanation:
Supplementary angles add up to 180 degrees, so cross of A. Vertical angles are directly across from each other, so cross off C. Corresponding angles are related to lines and a transversal which you don't have, so you can cross of D, leaving the answer as B.
Hopefully this helps - let me know if you have any questions!
Find the slope from the line of best fit y = 5 - 3x.
Answers
Answer:
slope = -3
Step-by-step explanation:
⭐ What is the equation of a line in slope intercept form?
\(y = mx+b\)m is the slope. It is always multiplied with the variable (x)b is the y-intercept. It is always the term without a variableThe given line of best fit is written in slope-intercept form. All we have to do is identify which term is the slope.
\(y = -3x + 5\)
-3 is the coefficient of x. Therefore, -3 is the slope.
Step-by-step explanation:
What is the equation of a line in slope
intercept form?
mr + b
m is the slope. It is always multiplied with
the variable (x)
b is the y-intercept. It is always the term
without a variable
The given line of best fit is written in slope-
intercept form. All we have to do is identify
which term is the slope.
Y
-30+5
-3 is the coefficient of x. Therefore, -3 is
the slope.
Rhoda is asked to graph this system of equations:
5x-6y=4
3y+2x=7
How many times will the lines intersect?
A. The lines will not intersect
B. The lines will intersect once.
C. There is no way to tell without graphing the lines first.
D. The lines will intersect infinitely many times, because they are identical.
Answer back fast!
I will award Brainliest too!
Answers
Answer: B. The lines will intersect once.
Step-by-step explanation:
Multiplying the bottom equation by 2, we get 6y+4x=14.
Adding this to the first equation, this gives 9x=18, and thus x=2.
Therefore, since this means there will be 1 solution, the lines will intersect once.
On a piece of paper graph f(x) = 3x. Then determine which answer choice matches the graph you drew

Answers
Answer:
--
Step-by-step explanation:
Show all the options please
Not able to see all options
Show that the path of a moving point parallel to the axes of x and y with velocitiesu +
ey andv + ex is a conic section
Answers
We have shown that the path of a moving point with velocities u + ey and v + ex, parallel to the axes of x and y, is either a line (when v - \(e^2\) ≠ 0) or a horizontal line (when v - \(e^2\) = 0), both of which are conic sections.
To show that the path of a moving point parallel to the axes of x and y with velocities u + ey and v + ex is a conic section, we can analyze the motion of the point using the principles of calculus and conic sections.
Let's denote the position of the point at any given time t as (x, y). We are given that the velocities along the x and y axes are u + ey and v + ex, respectively. This means that the derivatives of x and y with respect to time, dx/dt and dy/dt, can be expressed as:
dx/dt = u + ey
dy/dt = v + ex
Now, let's integrate these expressions to obtain x and y as functions of t. Integrating dx/dt with respect to t gives:
x = ut + eyt + C1
Similarly, integrating dy/dt with respect to t gives:
y = vt + ext + C2
Where C1 and C2 are constants of integration.
Now, we can eliminate the parameter t by expressing t in terms of x and y. From the equation y = vt + ext + C2, we can solve for t:
t = (y - ext - C2) / v
Substituting this value of t into the equation for x, we get:
x = u[(y - ext - C2) / v] + ey[(y - ext - C2) / v] + C1
Simplifying this equation, we obtain:
vx - u - evx + ue + vy - \(e^2\)x - eyC2 = C1v
Rearranging the terms, we get:
vx - vy + ue + evx - \(e^2\)x = C1v + eyC2 - u
Let's define new constants A = ue + ev and B = C1v + eyC2 - u. The equation then becomes:
(v - \(e^2\))x + (u + ev)y = A + B
This equation is in the standard form of a conic section, specifically a line. However, we can manipulate this equation further to reveal other possible conic sections.
Let's consider the case when v - \(e^2\) ≠ 0. In this case, we can divide both sides of the equation by v - \(e^2\), yielding:
x + [(u + ev)/(v - \(e^2\))]y = (A + B)/(v - \(e^2\))
Now, let's define another constant C = (u + ev)/(v -\(e^2\)) and rewrite the equation as:
x + Cy = D
Where D = (A + B)/(v - \(e^2\)).
This equation represents a line in the x-y plane.
On the other hand, if v - \(e^2\) = 0, the equation becomes:
0x + (u + ev)y = A + B
This simplifies to:
(u + ev)y = A + B
Which is a horizontal line parallel to the x-axis.
Therefore, we have shown that the path of a moving point with velocities u + ey and v + ex, parallel to the axes of x and y, is either a line (when v - \(e^2\) ≠ 0) or a horizontal line (when v - \(e^2\) = 0), both of which are conic sections.
for such more question on horizontal line
https://brainly.com/question/25705666
#SPJ11
Determine which pair of points has a negative slope.
a
(-10, -3), (-7, 6)
c. (7, 7), (-8, 1)
b. (5,2), (-9,-10)
d. (2,9), (-3,-1)
Answers
Answer:
We conclude that all the pairs of points have positive slopes.
Thus, there is NO pair of points that has a negative slope.
Step-by-step explanation:
a)
Determining the slope between (-10, -3), (-7, 6)
\(\mathrm{Slope}=\frac{y_2-y_1}{x_2-x_1}\)
\(\left(x_1,\:y_1\right)=\left(-10,\:-3\right),\:\left(x_2,\:y_2\right)=\left(-7,\:6\right)\)
\(m=\frac{6-\left(-3\right)}{-7-\left(-10\right)}\)
\(m=3\)
b)
Determining the slope between (7, 7), (-8, 1)
\(\mathrm{Slope}=\frac{y_2-y_1}{x_2-x_1}\)
\(m=\frac{1-7}{-8-7}\)
\(m=\frac{2}{5}\)
c)
Determining the slope between (5,2), (-9,-10)
\(\mathrm{Slope}=\frac{y_2-y_1}{x_2-x_1}\)
\(m=\frac{-10-2}{-9-5}\)
\(m=\frac{6}{7}\)
d)
Determining the slope between (2,9), (-3,-1)
\(\mathrm{Slope}=\frac{y_2-y_1}{x_2-x_1}\)
\(m=\frac{-1-9}{-3-2}\)
\(m=2\)
We conclude that all the pairs of points have positive slopes.
Thus, there is NO pair of points that has a negative slope.
what's the formula for sum of
geometric progression
Answers
Answer:
Hello,
Step-by-step explanation:
\(u_1\ is\ the \ first\ term\ of\ the\ gp\\q\ is \ the\ common\ ratio\\\\\\\boxed{u_n=u_1*\dfrac{q^n-1}{q-1} }\)
Help this is due today!!!

Answers
Answer:
m=11
Step-by-step explanation:
m=30-12-7
Answer:
m = 11
Step-by-step explanation:
Easiest way to find out is by doing 12+7 which is 19, then you do 30-19 which gets 11.
A number is _____ by another number if the quotient is a counting number and the remainder is zero.
Answers
Answer:
56888
Step-by-step explanation:
guy is unavailable right now because this video is not available