How to solve 4x+25+10
Answers
Answer:
first you would move the x to the other side of the equation so it would be 25+10= -4x next you would add the 25 and the 10 and that would be 35=-4x than you divide 35 by -4 and your answer would be -8.75
Related Questions
length of a rectangle is 3 times its width. If the length is 9cm what is the area of the rectangle
Answers
Answer:
I think it's 27
because length is 3 times its width
write two numbers that multiply to the value on top and add to the value on bottom.
top number : 56
bottom number:-15
Answers
Answer:
7 x 8 = 56
-3 x -5 or -5 + -5 + -5 = -15
Step-by-step explanation:
The numbers that result in the top and bottom numbers are: -7 and -8
System of Linear EquationsSystem of linear equations is the given term math for two or more equations with the same variables. The solution of these equations represents the point at which the lines intersect.
You should convert the given text into linear equations.
x*y=56 (1)
x+y=-15 (2)
For equation 2, you have x=-15-y. Thus, you can replace this variable into equation 1.
(-15-y)*y=56
-15y-y²=56
-y²-15y-56=0
You find a quadratic equation. Solving this equation:
\(y_{1,\:2}=\frac{-\left(-15\right)\pm \sqrt{\left(-15\right)^2-4\left(-1\right)\left(-56\right)}}{2\left(-1\right)}\\ \\ y_{1,\:2}=\frac{-\left(-15\right)\pm \:1}{2\left(-1\right)}\\\)
\(y_1=\frac{-\left(-15\right)+1}{2\left(-1\right)}=-8\\ \\ y_2=\frac{-\left(-15\right)-1}{2\left(-1\right)}=-7\)
For equation 2,
For y=-8x+y=-15
x+(-8)=-15
x=-15+8=-7
For y=-7 x+y=-15 x+(-7)=-15x=-15+7=-8Read more about the quadratic function here:
brainly.com/question/1497716
#SPJ2
A circle has a radius of 30 cm and a central angle that measures 312 degrees. Find the length of the arc defined by this central angle
Answers
The length of the arc defined by the central angle of 312 degrees is 26π cm.
The formula for the arc length of a circle is given by:
L = (θ/360) × 2πr
where L is the length of the arc, θ is the central angle in degrees, and r is the radius of the circle.
Substituting the given values, we get:
L = (312/360) × 2π(30)
L = (26/30) × π × 30
L = 26π cm
Therefore, the length of the arc defined by the central angle of 312 degrees is 26π cm.
To learn more on Circles click:
https://brainly.com/question/11833983
#SPJ1
May I have help on This question I’ll give you brainliest

Answers
What is the solution to the equation below round your answer to two decimal decimal places log4 x=2.1
A. x=8.40
B. x=18.38
C. x=8.17
D. x=19.45
Answers
Answer:
B 18.38
Step-by-step explanation:
log4x = 2.1
logx/log4 = 2.1
logx = log(4) x 2.1
logx = 1.2643
x = antilog(1.2643)
x = 18.38 (to 2 d.p)
Answer:
X=18.38
Step-by-step explanation:
Solve each problem.
a. What is -4.3 - (-6.8)?
b. What is
is 13 + (-210?
noints lose anothe
Answers
Hope this help!
B:-197
Merry Christmas
algebraic expression for “six more than the quantity d times two.”
Answers
Answer:
6 + (d * 2)
Step-by-step explanation:
You are adding 6 to the equation after the amount d times 2. In that case, a parentheses is required to round up d * 2.
A person leaves home and walks 4 miles west, then 5 miles southwest.
How far from home is she?
miles
In what direction must she walk to head directly home?
degrees North of East

Answers
The person is approximately 8.43 miles from home, and they need to walk in the direction of approximately 26.6 degrees east of north to head directly home.
To determine the distance from home, we can use the concept of vector addition. The person walks 4 miles west, which can be represented as a vector (-4, 0) in a coordinate plane. Then, they walk 5 miles southwest, which can be represented as a vector (-3.54, -3.54) since southwest is a combination of west and south. Adding these two vectors together gives us (-7.54, -3.54).
To find the magnitude or distance from home, we use the Pythagorean theorem. The distance is given by sqrt((-7.54)^2 + (-3.54)^2) = 8.43 miles (approximately).
To determine the direction to head directly home, we need to find the angle between the vector (-7.54, -3.54) and the positive x-axis. We can use trigonometry to find this angle. The tangent of the angle is given by the ratio of the y-coordinate to the x-coordinate, which is -3.54 / -7.54. Taking the inverse tangent of this value gives us approximately 26.6 degrees.
For more such questions on direction
https://brainly.com/question/30016405
#SPJ8
tg105°-cotg105° = ?
Please help fast!!! Please
Answers
Using only the trig ratios of 45 and 60 degrees, we use angle-sum to compute \(\tan 105^\circ=\tan(60^\circ+45^\circ)=\frac{\tan 60^\circ+\tan 45^\circ}{1-\tan 60^\circ\tan 45^\circ}=\frac{\sqrt{3}+1}{1-\sqrt{3}}=-2-\sqrt{3},\) so \(\cot 105^\circ=\frac{1}{\tan 105^\circ}=-2+\sqrt{3}\) and \(\tan 105^\circ-\cot105^\circ=\boxed{-2\sqrt{3}}.\)
Question 9 A cylindrical beaker with a base radius of 3 inches and a height of 11 Inches weighs 3.5 ounces when empty. The beaker is filled with water to one inch from the top. If one cubic Inch of water weighs 0.6 ounce, how many ounces does the beaker weigh, including the weight of the cylindrical beaker? Explain how you found your answer. Round to the nearest tenth.
Answers
The weight of the beaker, including the weight of the water, is approximately 173.1 ounces when rounded to the nearest tenth. To find the weight of the beaker when filled with water, including the weight of the cylindrical beaker itself, we need to calculate the weight of the water and add it to the weight of the empty beaker.
First, let's find the volume of the water in the beaker. The beaker is filled to one inch from the top, which means the height of the water is 11 - 1 = 10 inches.
The volume of the water can be calculated using the formula for the volume of a cylinder: \(V = \pi r^2h\), where r is the radius and h is the height.
\(V = \pi (3^2)(10) = 90\pi\) cubic inches
Next, we need to find the weight of the water. Given that one cubic inch of water weighs 0.6 ounces, we can multiply the volume of the water by 0.6 to get the weight of the water.
Weight of water = 90π x 0.6 = 54π ounces
Finally, we need to add the weight of the empty beaker, which is 3.5 ounces, to the weight of the water.
Weight of beaker with water = 54π + 3.5 ounces
To find the approximate value, we can use the value of π as 3.14.
Weight of beaker with water ≈ 54 x 3.14 + 3.5 ≈ 169.56 + 3.5 ≈ 173.06 ounces
For more such questions weight
on https://brainly.com/question/2335828
#SPJ8
PLEASE I NEED HELP FAST ITS THE LAST QUESTION AND I DONT KNOW HOW TO SOLVE IT
A storage unit in the shape of a rectangular prism is 9 feet tall and 4 1/4 feet wide. the length of the storage until is twice the width. which measurement is closest to the volume of the storage until in cubic feet?
Answers
Answer:
9 x 4 1/4 x 8 1/2 = 325 1/8 cubic feet.
4 1/4 x 2 = 8 1/2
5 Signs for science project displays are cut of poster board that measure 1 yard on each side. Each sign is-yard long and-yard wide. How ma signs can be cut from 1 piece of poster board? Wh the area of each sign? Show your work.
Answers
Answer:
\(\text{27}\)
Step-by-step explanation:
Given that :
\(\text{Dimension of poster board} = 1 \ \text{yd} \ \text{by} \ 1 \ \text{yd}\)
\(\text{Dimension of each poster board} = \dfrac{1}{3} \ \text{yd} \ \text{by} \ \dfrac{1}{9} \ \text{yd}\)
Number of poster signs that can be cut :
\(\text{Area of poster sign} = \dfrac{1}{3} \times \dfrac{1}{9} = \dfrac{1}{27} \ \text{yard}^2\)
\(\text{Area of poster board} = 1 \ \text{yard}^2\)
Number of poster signs that can be cut :
\(\dfrac{\text{Area of poster board}}{\text{Area of poster sign}}\)
\(1 \ \text{yard}^2\div (\dfrac{1}{27} ) \ \text{yard}^2\)
\(1 \div \dfrac{1}{27}\)
\(1 \times \dfrac{27}{1}\)
\(\bold{= 27 \ poster \ signs}\)
7. There are 1000 different components in the system that your department has just designed. The objective is that for each of the systems that you deliver to a customer, it should have a probability of 0.999 of functioning properly. Your system is such that at most 8 components can be bad for it to still function. What must be the maximum probability for each of your components to fail for you to achieve your objective
Answers
Answer:
The maximum probability for each of the components in a system to fail, for you to still achieve your objective, is 0.008992
Step-by-step explanation:
- There are 1,000 different components in each system.
- The Objective:
Each system should have a 0.999 probability of functioning properly. In other words, your department (or you) expects that each system will have a high probability of functioning properly, hence the closeness of 0.999 to 1.
- Each system is such that at most 8 components out of 1,000 can be bad, for it to still function.
- Question:
What must be the maximum probability for each component in a system to fail, for the system to still have a 0.999 probability of functioning properly?
ANSWER:
When the question says maximum, you need to assume that for each system, 8 components are actually bad!
1000 - 8 = 992
So with 992 components (at least or minimum) functioning, a system will still function.
Next Step:
Since the objective (the expected probability) for a system to function is 0.999, the probability of each of the minimum 992 components to function (which is same as the maximum probability for each of the 1,000 components to function) is
992/1000 × 0.999
=0.992 × 0.999
=0.991008
Now, remember that the question says fail, not succeed. So, if the figure above is the maximum success rate for each of the 1,000 component parts (same as the success rate for each of the minimum of 992 component parts), then the failure rate or probability is (1 - 0.991008 = 0.008992).
FINAL ANSWER:
The maximum probability for each of the components in a system to fail, for you to still achieve your objective, is 0.008992
Order equivalent equations of 2(−3) = 4 2 x - 3 = 4 x to solve for x .

Answers
The missing 3 steps for the given equivalent equation are as follows:
1st step: 2x - 6 = 4x
2nd step: -6 = 2x
3rd step: -3 = x
What are equivalent equations?Algebraic equations with equivalent solutions or roots are called equivalent equations.
An analogous equation is one that is created by adding or removing the identical quantity or expression from both sides of a given equation.
An equation is equivalent if both sides are multiplied or divided by the same non-zero value.
So, we have the equation:
2(x-3) = 4x
Now, solve further as follows:
2(x-3) = 4x
1st step: 2x - 6 = 4x
2nd step: -6 = 2x
3rd step: -3 = x
Therefore, the missing 3 steps for the given equivalent equation are as follows:
1st step: 2x - 6 = 4x
2nd step: -6 = 2x
3rd step: -3 = x
Know more about equivalent equations here:
https://brainly.com/question/2972832
#SPJ1
Write the following equation into logarithmic form. 5=3x
Answers
Answer:
\(log_35=x\)
Step-by-step explanation:
I am going to assume you meant \(5=3^x\)
When converting exponential equations into logarithmic form, remember this: \(y = log_bx\) is equivalent to \(x = b^y\)
7. N.CN.7 Determine the zeroes for the equation below. Select all that apply.
x² - 6x +13=0
A. 1
B. 5
C. 13
D. -3 + 2i
E. 3+2i
F. 3+4i
G. 6 + 4i
H. 3-21
I .6-41
Answers
Answer:
D. -3 + 2i and E. 3+2i are the zeroes for the equation.
Step-by-step explanation:
tha distance y that cam swims in x minutes is a proportional relationship. the data from his most recent swims are shown in the table. Brittney calculates that she swims 51.3 meters per minutes. Who is the lower swimmers?

Answers
Step-by-step explanation:
Do not know sorry
........ M
GIVING BRAINLIST PLEASE HELP!!!
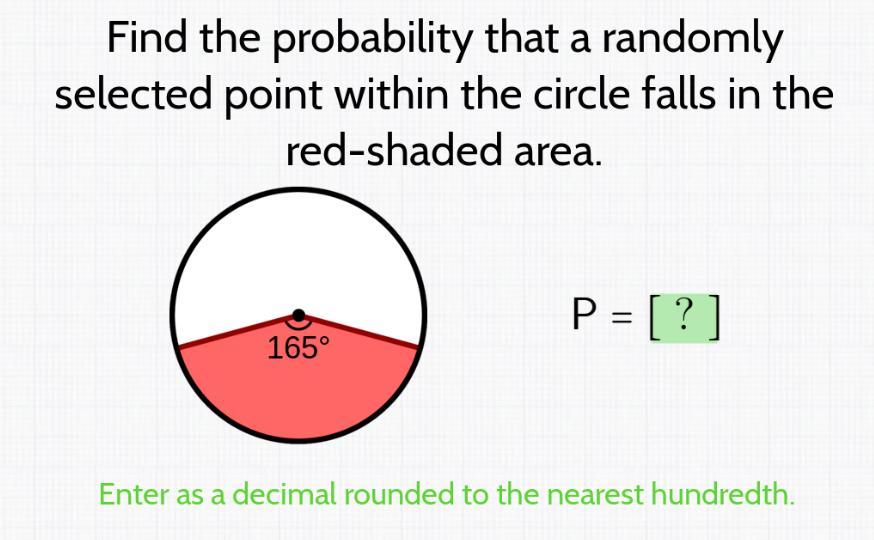
Answers
The probability that a randomly selected point within the circle would fall in the red- shaded area is 45. 833 %
How to find the probability ?The arc that is covered by the red - shaded area in the circle has a degree measure of 165 degrees. This is out of the total circle angle measure of 360 degrees.
This therefore means that the probability that a randomly selected point within the circle would fall in the red- shaded area can be found to be :
= Angle measure of red - shaped area / Total area x 100 %
= 165 / 360 x 100 %
=0. 45833 x 100 %
= 45. 833 %
Find out more on probability at https://brainly.com/question/22690728
#SPJ1
Select all the expressions that are rational numbers.
a. 3.14159…
b. –9.1234567123…
c. –9.293847210103938…
d. 227
e. –26
Answers
Answer:
d,e
Step-by-step explanation:
rational numbers are positive and negative whole numbers.
Answer:
d,e
Step-by-step explanation:
Which value should he use for X? Round to the nearest hundredth. 0.89 0.90 0.92 0.96
Answers
The number nearest to hundredth among the given options is 0.96
What is rounding off?To change a number into an approximation having fewer significant digits.
Given are the numbers 0.89, 0.90, 0.92 and 0.96
We need to find which one of these is the nearest hundredth
Among all the options, only 0.96 is the number which is nearest to 100.
Hence, The number nearest to hundredth among the given options is 0.96
For more references on rounding off, click;
https://brainly.com/question/13391706
#SPJ2
Which is true about investments and risk?
Answers
Answer:
Every investment carries some degree of risk, All investments carry some degree of risk. Stocks, bonds, mutual funds, and exchange-traded funds can lose value, even all their value, if market conditions sour. Even conservative, insured investments, such as certificates of deposit (CDs) issued by a bank or credit union, come with inflation risk. They may not earn enough over time to keep pace with the increasing cost of living.
Step-by-step explanation:
Two buses leave a station at the same time and travel in opposite directions. One bus travels 15 km/h slower than the other. If the two buses are 1393 kilometers apart after 7 hours, what is the rate of each bus?
Answers
First Bus = x
Second Bus = x-15
They are going in opposite directions, so, we have to add the speeds:
x+x-15 = 2x-15
Time = 7 hours
Distance = speed * time
1393 = (2x-15)7
1393 = 2x(7)-15(7)
1393 = 14x-105
1393+105 = 14x
1498 =14x
1498/14 = x
107 =x
First bus: 107 km/h
Second bus = x-15 = 107-15 = 92 km/h
Which fraction is closest to zero?

Answers
Answer:
8/12=0.667
5/8=0.625
6/10=0.6
2/3=0.667
Step-by-step explanation:
6/10 would be your answer being that it is the smallest of them all
a machine is used to fill bags with a popular brand of trail mix. the machine is calibrated so the distribution of the weights of the bags of trail mix is normal, with mean 240 grams and standard deviation 3 grams. of the following, which is the least weight of a bag in the top 5 percent of the distribution? responses
Answers
The top five percent of the distribution's lowest weight as calculated from the given data for a bag is 246.
Average population = 240
Standard deviation for the population; 3
Z-score can be calculated as ,
z = (x' - μ)/σ
Now, in order to determine which of the top 5 values in the distribution has the least weight, we will use the significance threshold of 1 - 0.05/2 = 0.025.
Z-score is 1.96 at significance level 0.025.
Thus;
1.96 = (x' - 240)/3
3 × 1.96 = x' - 240
x' = 240 + 5.88
x' = 245.88
Getting close to a whole number results ,
x' = 246
The two z-score tables are as follows:
Positive Z Score Table: The observed value is greater than the average of all values.
An observed value that is below the mean of all values is shown by a negative Z score table.
To learn more about z-score
brainly.com/question/25638875
#SPJ4
Mofor has homework assignments in five subjects. He only has time to do two of
them.
Answers
The decision of which two homework assignments to complete depends on Mofor's individual circumstances and priorities.
If Mofor only has time to do two homework assignments out of the five subjects, he will need to choose which subjects to prioritize. The specific subjects he chooses to work on will depend on various factors such as his strengths, weaknesses, upcoming deadlines, and personal preferences. Here are a few strategies he could consider:
1. Prioritize based on importance: Mofor can prioritize the homework assignments that carry more weight in terms of grades or have upcoming deadlines. This way, he ensures that he completes the assignments that have a higher impact on his overall academic performance.
2. Focus on challenging subjects: If Mofor finds certain subjects more difficult or time-consuming, he can prioritize those assignments to allocate more time and effort to them. This approach allows him to concentrate on improving his understanding and performance in subjects that require extra attention.
3. Balance workload: Mofor can choose to distribute his efforts evenly across subjects, selecting two assignments from different subjects. This strategy ensures that he maintains a balanced workload and avoids neglecting any particular subject.
The decision of which two homework assignments to complete depends on Mofor's individual circumstances and priorities. It is essential for him to consider his academic goals, time constraints, and personal strengths to make an informed decision.
For more such questions on homework
https://brainly.com/question/28521601
#SPJ8
a college student is saving money to buy a laptop. the student has $85 saved and saves $35 each week. The function a(t)=35t + 85 represents the amount of money the college student has saved for the laptop after t weeks. The student receives $50 as a birthday gift .
If the function f(t) = a(t) +50 represents the total amount the student has saved , which best describes the transformation from a(t) to f(t)?

Answers
Answer:
B a vertical translation 50units right
At a furniture store, 20% of chairs are blue, 50% orange and 30% black. A blue chair has a 20% probability of being comfortable. A chair that is not blue has a 5% probability of being comfortable. What is the probability that a comfortable chair in the store is blue?
Answers
The probability that a comfortable chair in the store is blue is 4%
How to determine the probability?From the question, we have the following parameters that can be used in our computation:
Proportion of blue chairs = 20%
Proportion of orange chairs = 50%
Proportion of black chairs = 30%
Comfortable Blue chairs = 20%
Comfortable non-blue chairs = 5%
The required probability is then calculated as
Probability = Proportion of blue chairs x Comfortable Blue chairs
Substitute the known values in the above equation, so, we have the following representation
Probability = 20% * 20%
Evaluate
Probability = 4%
Hence, the probability is 4%
Read more about probability at
https://brainly.com/question/251701
#SPJ1
determine whether the function is differentiable (curve has a tangent line) at the indicated point. If it does, find its derivative. if not explain why not.

Answers
Let's see the sketch:
The function is differentiable at x = 0 as you can see from the graph. It doesn't have any cusp or discontinuity.
Now, to find the derivate, we use the bottom function (as x = 0 falls in this).
So,
\(\begin{gathered} f(x)=x^2-x \\ f^{\prime}(x)=2x-1 \\ f^{\prime}(0)=2(0)\text{ -1} \\ f^{\prime}(0)=-1 \end{gathered}\)The derivative is -1

Let z=3+i,
then find
a. Z²
b. |Z|
c.\(\sqrt{Z}\)
d. Polar form of z
Answers
Given z = 3 + i, right away we can find
(a) square
z ² = (3 + i )² = 3² + 6i + i ² = 9 + 6i - 1 = 8 + 6i
(b) modulus
|z| = √(3² + 1²) = √(9 + 1) = √10
(d) polar form
First find the argument:
arg(z) = arctan(1/3)
Then
z = |z| exp(i arg(z))
z = √10 exp(i arctan(1/3))
or
z = √10 (cos(arctan(1/3)) + i sin(arctan(1/3))
(c) square root
Any complex number has 2 square roots. Using the polar form from part (d), we have
√z = √(√10) exp(i arctan(1/3) / 2)
and
√z = √(√10) exp(i (arctan(1/3) + 2π) / 2)
Then in standard rectangular form, we have
\(\sqrt z = \sqrt[4]{10} \left(\cos\left(\dfrac12 \arctan\left(\dfrac13\right)\right) + i \sin\left(\dfrac12 \arctan\left(\dfrac13\right)\right)\right)\)
and
\(\sqrt z = \sqrt[4]{10} \left(\cos\left(\dfrac12 \arctan\left(\dfrac13\right) + \pi\right) + i \sin\left(\dfrac12 \arctan\left(\dfrac13\right) + \pi\right)\right)\)
We can simplify this further. We know that z lies in the first quadrant, so
0 < arg(z) = arctan(1/3) < π/2
which means
0 < 1/2 arctan(1/3) < π/4
Then both cos(1/2 arctan(1/3)) and sin(1/2 arctan(1/3)) are positive. Using the half-angle identity, we then have
\(\cos\left(\dfrac12 \arctan\left(\dfrac13\right)\right) = \sqrt{\dfrac{1+\cos\left(\arctan\left(\dfrac13\right)\right)}2}\)
\(\sin\left(\dfrac12 \arctan\left(\dfrac13\right)\right) = \sqrt{\dfrac{1-\cos\left(\arctan\left(\dfrac13\right)\right)}2}\)
and since cos(x + π) = -cos(x) and sin(x + π) = -sin(x),
\(\cos\left(\dfrac12 \arctan\left(\dfrac13\right)+\pi\right) = -\sqrt{\dfrac{1+\cos\left(\arctan\left(\dfrac13\right)\right)}2}\)
\(\sin\left(\dfrac12 \arctan\left(\dfrac13\right)+\pi\right) = -\sqrt{\dfrac{1-\cos\left(\arctan\left(\dfrac13\right)\right)}2}\)
Now, arctan(1/3) is an angle y such that tan(y) = 1/3. In a right triangle satisfying this relation, we would see that cos(y) = 3/√10 and sin(y) = 1/√10. Then
\(\cos\left(\dfrac12 \arctan\left(\dfrac13\right)\right) = \sqrt{\dfrac{1+\dfrac3{\sqrt{10}}}2} = \sqrt{\dfrac{10+3\sqrt{10}}{20}}\)
\(\sin\left(\dfrac12 \arctan\left(\dfrac13\right)\right) = \sqrt{\dfrac{1-\dfrac3{\sqrt{10}}}2} = \sqrt{\dfrac{10-3\sqrt{10}}{20}}\)
\(\cos\left(\dfrac12 \arctan\left(\dfrac13\right)+\pi\right) = -\sqrt{\dfrac{10-3\sqrt{10}}{20}}\)
\(\sin\left(\dfrac12 \arctan\left(\dfrac13\right)+\pi\right) = -\sqrt{\dfrac{10-3\sqrt{10}}{20}}\)
So the two square roots of z are
\(\boxed{\sqrt z = \sqrt[4]{10} \left(\sqrt{\dfrac{10+3\sqrt{10}}{20}} + i \sqrt{\dfrac{10-3\sqrt{10}}{20}}\right)}\)
and
\(\boxed{\sqrt z = -\sqrt[4]{10} \left(\sqrt{\dfrac{10+3\sqrt{10}}{20}} + i \sqrt{\dfrac{10-3\sqrt{10}}{20}}\right)}\)
Answer:
\(\displaystyle \text{a. }8+6i\\\\\text{b. }\sqrt{10}\\\\\text{c. }\\\sqrt{\sqrt{\frac{5}{2}}+\frac{3}{2}}+i\sqrt{\frac{\sqrt{10}-3}{2}},\\-\sqrt{\sqrt{\frac{5}{2}}+\frac{3}{2}}-i\sqrt{\frac{\sqrt{10}-3}{2}}\\\\\\\text{d. }\\\text{Exact: }z=\sqrt{10}\left(\cos\left(\arctan\left(\frac{1}{3}\right)\right), i\sin\left(\arctan\left(\frac{1}{3}\right)\right)\right),\\\text{Approximated: }z=3.16(\cos(18.4^{\circ}),i\sin(18.4^{\circ}))\)
Step-by-step explanation:
Recall that \(i=\sqrt{-1}\)
Part A:
We are just squaring a binomial, so the FOIL method works great. Also, recall that \((a+b)^2=a^2+2ab+b^2\).
\(z^2=(3+i)^2,\\z^2=3^2+2(3i)+i^2,\\z^2=9+6i-1,\\z^2=\boxed{8+6i}\)
Part B:
The magnitude, or modulus, of some complex number \(a+bi\) is given by \(\sqrt{a^2+b^2}\).
In \(3+i\), assign values:
\(a=3\) \(b=1\)\(|z|=\sqrt{3^2+1^2},\\|z|=\sqrt{9+1},\\|z|=\sqrt{10}\)
Part C:
In Part A, notice that when we square a complex number in the form \(a+bi\), our answer is still a complex number in the form
We have:
\((c+di)^2=a+bi\)
Expanding, we get:
\(c^2+2cdi+(di)^2=a+bi,\\c^2+2cdi+d^2(-1)=a+bi,\\c^2-d^2+2cdi=a+bi\)
This is still in the exact same form as \(a+bi\) where:
\(c^2-d^2\) corresponds with \(a\) \(2cd\) corresponds with \(b\)Thus, we have the following system of equations:
\(\begin{cases}c^2-d^2=3,\\2cd=1\end{cases}\)
Divide the second equation by \(2d\) to isolate \(c\):
\(2cd=1,\\\frac{2cd}{2d}=\frac{1}{2d},\\c=\frac{1}{2d}\)
Substitute this into the first equation:
\(\left(\frac{1}{2d}\right)^2-d^2=3,\\\frac{1}{4d^2}-d^2=3,\\1-4d^4=12d^2,\\-4d^4-12d^2+1=0\)
This is a quadratic disguise, let \(u=d^2\) and solve like a normal quadratic.
Solving yields:
\(d=\pm i \sqrt{\frac{3+\sqrt{10}}{2}},\\d=\pm \sqrt{\frac{{\sqrt{10}-3}}{2}}\)
We stipulate \(d\in \mathbb{R}\) and therefore \(d=\pm i \sqrt{\frac{3+\sqrt{10}}{2}}\) is extraneous.
Thus, we have the following cases:
\(\begin{cases}c^2-\left(\sqrt{\frac{\sqrt{10}-3}{2}}\right)^2=3\\c^2-\left(-\sqrt{\frac{\sqrt{10}-3}{2}}\right)^2=3\end{cases}\\\)
Notice that \(\left(\sqrt{\frac{\sqrt{10}-3}{2}}\right)^2=\left(-\sqrt{\frac{\sqrt{10}-3}{2}}\right)^2\). However, since \(2cd=1\), two solutions will be extraneous and we will have only two roots.
Solving, we have:
\(\begin{cases}c^2-\left(\sqrt{\frac{\sqrt{10}-3}{2}}\right)^2=3 \\c^2-\left(-\sqrt{\frac{\sqrt{10}-3}{2}}\right)^2=3\end{cases}\\\\c^2-\sqrt{\frac{5}{2}}+\frac{3}{2}=3,\\c=\pm \sqrt{\sqrt{\frac{5}{2}}+\frac{3}{2}\)
Given the conditions \(c\in \mathbb{R}, d\in \mathbb{R}, 2cd=1\), the solutions to this system of equations are:
\(\left(\sqrt{\sqrt{\frac{5}{2}}+\frac{3}{2}}, \sqrt{\frac{\sqrt{10}-3}{2}}\right),\\\left(-\sqrt{\sqrt{\frac{5}{2}}+\frac{3}{2}},- \frac{\sqrt{10}-3}{2}}\right)\)
Therefore, the square roots of \(z=3+i\) are:
\(\sqrt{z}=\boxed{\sqrt{\sqrt{\frac{5}{2}}+\frac{3}{2}}+i\sqrt{\frac{\sqrt{10}-3}{2}} },\\\sqrt{z}=\boxed{-\sqrt{\sqrt{\frac{5}{2}}+\frac{3}{2}}-i\sqrt{\frac{\sqrt{10}-3}{2}}}\)
Part D:
The polar form of some complex number \(a+bi\) is given by \(z=r(\cos \theta+\sin \theta)i\), where \(r\) is the modulus of the complex number (as we found in Part B), and \(\theta=\arctan(\frac{b}{a})\) (derive from right triangle in a complex plane).
We already found the value of the modulus/magnitude in Part B to be \(r=\sqrt{10}\).
The angular polar coordinate \(\theta\) is given by \(\theta=\arctan(\frac{b}{a})\) and thus is:
\(\theta=\arctan(\frac{1}{3}),\\\theta=18.43494882\approx 18.4^{\circ}\)
Therefore, the polar form of \(z\) is:
\(\displaystyle \text{Exact: }z=\sqrt{10}\left(\cos\left(\arctan\left(\frac{1}{3}\right)\right), i\sin\left(\arctan\left(\frac{1}{3}\right)\right)\right),\\\text{Approximated: }z=3.16(\cos(18.4^{\circ}),i\sin(18.4^{\circ}))\)
Ashley has a points card for a movie theater.
• She receives 25 rewards points just for signing up.
• She earns 2.5 points for each visit to the movie theater.
• She needs 45 points for a free movie ticket.
How many visits must Ashley make to earn a free movie ticket?
Answers
Answer:
8
Step-by-step explanation:
45 points for a free movie - 25 points = 20 remaining points needed
20 / 2.5 = 8
She would need 8 visits to earn a free movie ticket.
Answer:
8
Step-by-step explanation:
25+2.5x=45
subtract 25 from each side
2.5x=20
divide both sides by 2.5
x=8