how many ways can six books be arranged on a shelf if one of the books is a dictionary and it must be on an end?
Answers
There are 120 ways to arrange the six books on a shelf if one of the books is a dictionary and it must be on one of the ends.
To find the number of ways the books can be arranged, we first consider the position of the dictionary.
Since the dictionary must be on one of the ends, it has two possible positions: the left end or the right end.
Once we fix the position of the dictionary, we have five remaining books to arrange on the shelf.
These five books can be arranged in 5! (5 factorial) ways, which means there are 5 × 4 × 3 × 2 × 1 = 120 possible arrangements.
Since the position of the dictionary was fixed at the beginning, each of the 120 arrangements corresponds to a unique arrangement of all six books on the shelf with the dictionary on one of the ends.
Therefore, the total number of ways to arrange the six books on the shelf, given that one of the books is a dictionary and it must be on one of the ends, is 120.
Learn more about factorial here:
https://brainly.com/question/9214272
#SPJ11
Related Questions
please help me for the brainliest answer

Answers
Answer:
1.17
Step-by-step explanation:
1 £ = 1.25 dollars
1 Euro = 1.07 dollars
=> 1 £ = (1.25/1.07) Euros = 1.17 Euros
Need help 10 points
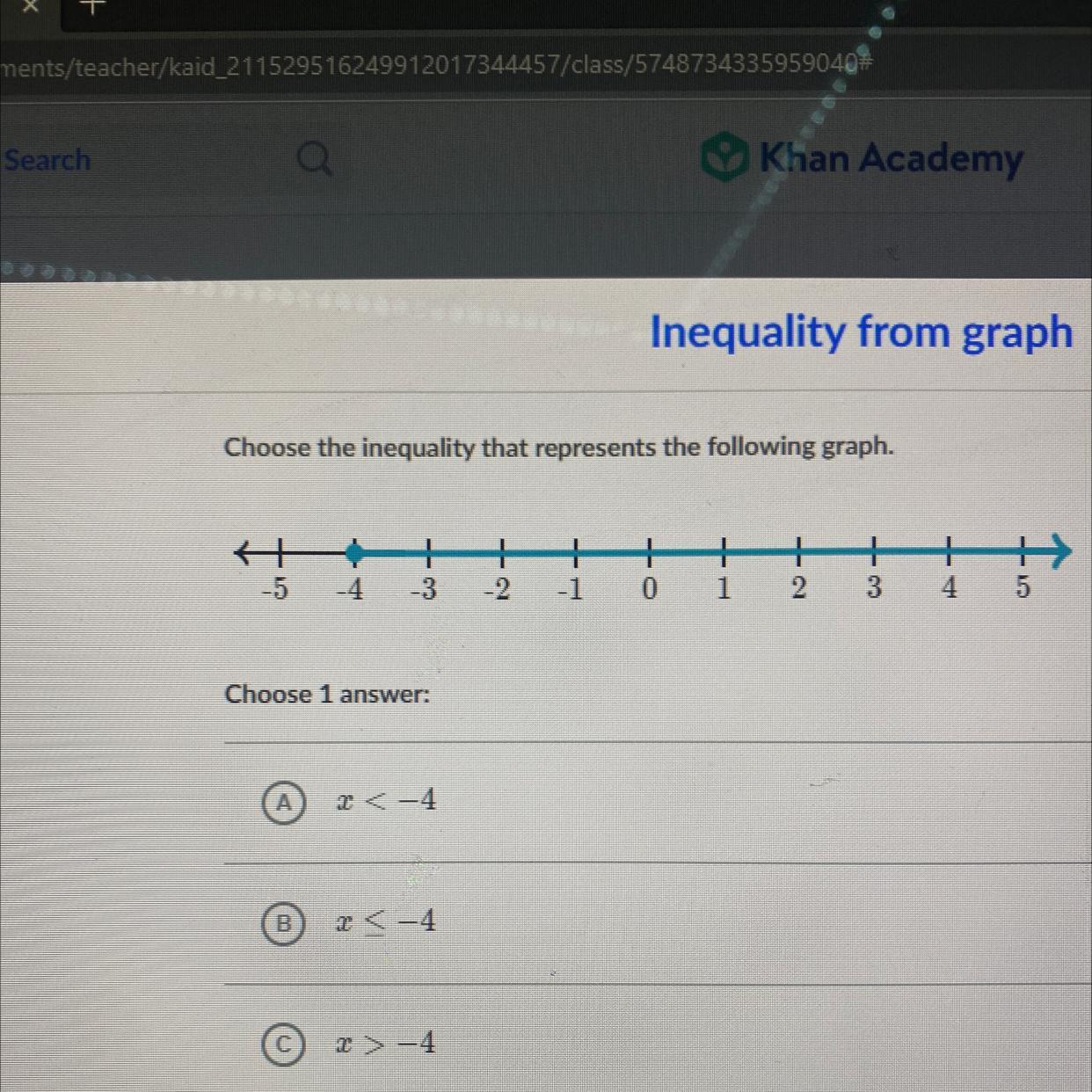
Answers
Answer:
have you missed out any option cause i doeant match with any of your options
Solve the following inequality:
m - 2 < - 8 or m/8 > 1

Answers
For the first equation you add 2 on both sides to get m < -6.
For the second you multiply by 8 on both sides to get m > 8
The answer is C.
Hope this helps
The following inequality of m - 2 < -8 or m/8 > 1 is m < -6 or m > 8.
Option C is the correct answer.
What is inequality?It is a statement of an ordered relationship
- greater than,
- greater than or equal to,
- less than,
- less than or equal to between two numbers or algebraic expressions.
We have,
m - 2 < -8 or m/8 > 1
Let's find m for each inequality.
m - 2 < -8
Adding 2 on both sides.
m - 2 + 2 < -8 + 2
m < -6 _____(1)
m/8 > 1
Multiply 8 on both sides.
8 x m/8 > 8 x 1
m > 8 _____(2)
From (1) and (2) we get,
m < -6 or m > 8
Thus,
The following inequality of m - 2 < -8 or m/8 > 1 is m < -6 or m > 8.
Option C is the correct answer.
Learn more about inequality here:
https://brainly.com/question/22010462
#SPJ2
Find the least number which when divisible by 20, 24, 32 and 38 leaves a remainder 5 in cach case
Answers
Answer:
18245
Step-by-step explanation:
We have to use L.C.M,
L.C.M(20,24,32,38)
2|20,24,32,38
2| 10 ,12 ,16 ,19
2| 5 , 6 , 8 , 19
2| 5 , 3 , 4 , 19
2| 5 , 3 , 2 , 19
L.C.M = 2 x 2 x 2 x 2 x 2 x 2 x 5 x 3 x 19
= 18240
Now for each case remainder is 5,
So the number is 18240+5
=> 18245
5. State if the following statements are true or false. If true, give a 1-3 line explanation; otherwise, provide a counter example or explanation. No rigorous formal justification needed. (a) The set {x∈R
n
∣Ax=b} is convex, where A∈R
m×n
,b∈R
m
. (b) The set {(x
1
,x
2
)∣x
2
≤3x
1
2
} is convex. (c) All polygons on the R
2
plane are convex. (Hint: A polygon is a plane figure formed with straight line segments.) (d) If S⊆R
2
is convex, then S must enclose a region of finite area. (e) If S
1
,S
2
⊆R
2
and S
1
∩S
2
=ϕ, then S
1
∪S
2
must be non-convex. (f) If S
1
,S
2
⊆R
2
and both S
1
,S
2
are closed, then S
1
∪S
2
must be non-convex.
Answers
(a) False. The set {x∈R^n | Ax=b} is not necessarily convex. It depends on the matrix A and the vector b. For example, if A is a non-convex matrix, then the set of solutions {x∈R^n | Ax=b} will also be non-convex.
(b) True. The set {(x₁,x₂) | x₂ ≤ 3x₁²} is convex. The inequality defines a downward parabolic region, and any line segment connecting two points within this region will lie entirely within the region. (c) False. Not all polygons on the R² plane are convex. For example, a polygon with a concave portion, such as a crescent shape, would not be convex.
(d) True. If S⊆R² is convex, then it must enclose a region of finite area. Convex sets do not have "holes" or disjoint parts, so they form a connected and bounded region. (e) False. If S₁⊆R² and S₂⊆R², and S₁∩S₂=ϕ (empty set), then S₁∪S₂ can be convex. If S₁ and S₂ are both convex sets that do not overlap, their union can still be a convex set. (f) True. If S₁⊆R² and S₂⊆R² are both closed sets, then their union S₁∪S₂ must also be closed. However, it may or may not be convex. The convexity of the union depends on the specific sets S₁ and S₂.
To learn more about vector click here: brainly.com/question/24256726
#SPJ11
Which ordered pair is a solution to the system?

Answers
Hope this helps :))
Please help!! Find the equation of variation given that y varies directly with x and y is 25 when x is 5

Answers
Answer:
y=5x
Step-by-step explanation:
If y is 25 and x is 5
25 = 5 (5)
25=25
what is the explicit formula for this sequence? -7,-3,1,5,…
Answers
Answer:
\(a_n=4n-11\)
Step-by-step explanation:
The common difference is \(d=4\) with the first term being \(a_1=-7\), so we can generate an explicit formula for this arithmetic sequence:
\(a_n=a_1+(n-1)d\\a_n=-7+(n-1)(4)\\a_n=-7+4n-4\\a_n=4n-11\)
let c be the positively oriented circle x2 y2=1. use green's theorem to evaluate the line integral ∫c11ydx 7xdy.
Answers
The value of the line integral ∫c (11y dx + 7x dy) is -4π. To evaluate the line integral ∫c (11y dx + 7x dy) using Green's theorem, we need to follow these steps:
1. Recognize that the given circle is x² + y² = 1, with a positive (counter-clockwise) orientation.
2. Green's theorem states that for a positively oriented, simple, closed curve C, ∫c (P dx + Q dy) = ∬D (Qx - Py) dA, where D is the region bounded by C, and P and Q are functions of x and y.
3. In our case, P = 11y and Q = 7x. So, we need to compute Py and Qx.
Py = ∂(11y)/∂y = 11, and Qx = ∂(7x)/∂x = 7.
4. Apply Green's theorem: ∫c (11y dx + 7x dy) = ∬D (7 - 11) dA = -4∬D dA.
5. Now, we need to find the area of the circle. The area of a circle is given by A = πr². Since the circle is x² + y² = 1, the radius r is 1. Thus, A = π(1)² = π.
6. The final step is to multiply the area by the constant factor from step 4: -4∬D dA = -4A = -4π.
So, the value of the line integral ∫c (11y dx + 7x dy) is -4π.
Learn more about value here:
brainly.com/question/30080140
#SPJ11
10) y=-x-4 4 5 1514 -

Answers
1/5 is the slope and we can use (-4,0) as a starting point.

compare adding and subtracting to multiplying and dividing bases with different exponents.
Answers
Exponent rules for addition and subtraction are identical to one another. As a reminder, all terms' bases must be the same in order to remove terms with exponents. All terms' exponents must be equal.
Define exponents.A number written as a superscript over another number is known as an exponent. In other words, it means that the base has been elevated to a particular level of power. Other names for the exponent are index and power. mn indicates that m has been multiplied by itself n times if m is a positive number and n is its exponent.
Given,
Adding and subtracting to multiplying and dividing bases with different exponents.
Exponent rules for addition and subtraction are identical to one another. As a reminder, all terms' bases must be the same in order to remove terms with exponents. All terms' exponents must be equal.
The exponents and variables must match in order to add exponents. The exponents are left constant while the variable coefficients are added. The addition only includes terms with the same variables and powers. Exponents can be multiplied and divided according to this rule.
To learn more about exponents, visit:
https://brainly.com/question/5497425
#SPJ1
PLEASE PLEASE ANSWER HELLPPPPP ILL GIVEBRAINLIEAT

Answers
Answer:
118
Step-by-step explanation:
inscribed angle = 1/2 intercepted arc, therefore an intercepted arc is twice its inscribed angle
\(59 \times 2 = 118\)
If it wouldn’t bother someone would someone also mind giving me the steps to get the answer?

Answers
Answer:
SA = 10,800 ft²
Step-by-step explanation:
To find the surface area of a rectangular prism, you can use the equation:
SA = 2 ( wl + hl + hw )
SA = surface area of rectangular prism
l = length
w = width
h = height
In the image, we are given the following information:
l = 40
w = 60
h = 30
Now, let's plug in the information given to us to solve for surface area:
SA = 2 ( wl + hl + hw)
SA = 2 ( 60(40) + 30(40) + 30(60) )
SA = 2 ( 2400 + 1200 + 1800 )
SA = 2 ( 5400 )
SA = 10,800 ft²
If this answer helped you, please leave a thanks!
Have a GREAT day!!!
Help yalll I really need help major time

Answers
Answer:
Annalise is correct because the outputs are closest when x = 1.35
Step-by-step explanation:
The solution to the equation 1/(x-1) = x² + 1 means the one x value that will make both sides equal. If we look at the table, notice how when x = 1.35, f(x) values are closest to each other for both equations, signifying that x = 1.35 is approximately the solution. Thus, Annalise is correct.
3. Kyle starts with $15.00 and saves $3.50
each day. What expression represents
the total amount Kyle saves?
A $3.50
B $15.00
C 3.5t + 15, where t is the number
of days
D 15t + 3.5, where t is the number
of days
Answers
Answer:
C 3.5t + 15, where t is the number
of days
Given f(x)=x*-x³-6x², for what values of x will f(x) > 0?
Answers
The values of x will f(x) > 0 for x < 0, and f(x) < 0 for -6 < x < 0 and x > -6.
To determine the values of x for which f(x) > 0, we need to find the intervals where the function is positive. Let's analyze the function f(x) = x*-x³-6x².
First, let's factor out an x from the expression to simplify it: f(x) = x(-x² - 6x).
Now, we can observe that if x = 0, the entire expression becomes 0, so f(x) = 0.
Next, we analyze the signs of the factors:
1. For x < 0, both x and (-x² - 6x) are negative, resulting in a positive product. Hence, f(x) > 0 in this range.
2. For -6 < x < 0, x is negative, but (-x² - 6x) is positive, resulting in a negative product. Therefore, f(x) < 0 in this range.
3. For x > -6, both x and (-x² - 6x) are positive, resulting in a negative product. Thus, f(x) < 0 in this range.
For such more questions on values
https://brainly.com/question/843074
#SPJ8
Write an expression.. NO LINKS
NEED HELP ASAP!!!

Answers
Answer:
-10.50*3
=-31.5
Write the coordinates of the vertices after a reflection over the line x = 1.

Answers
The coordinates of the vertices B, D and C after a reflection over the line x = 1 are B'(1,7), D'(1,6) and C'(-8, 7).
Explain about reflection about x axis:The picture M', whose coordinates are in the fourth quadrant and created when point M is mirrored in the x-axis, is (h, -k). As a result, we deduce that when a point is reflected along the x-axis, the x-coordinate stays constant while the y-coordinate changes to the negative.
As a result, M'(h, -k). is the image for point M (h, k)
Given data:
coordinates of the vertices before reflection:
B(1,7), D(1,6) and C(10, 7).
Reflection about x = 1.
As Point B and D lies on the line x = 1, their coordinates will not change.
C is 9 units to the right of the line x = 1 at (10, 7)
Thus, after reflection C will be 9 units to the left of the line x = 1 at (-8, 7).
Therefore, the coordinates of the vertices B, D and C after a reflection over the line x = 1 are B'(1,7), D'(1,6) and C'(-8, 7).
know more about the reflection about x axis:
https://brainly.com/question/24696463
#SPJ1
(Adding and Subtracting Rational Numbers MC)
Solve negative four minus one and three fifths.
five and three fifths
one and three fifths
four fifths
negative five and three fifths
Answers
Answer:
negative 5 and 3/5
Step-by-step explanation:
-4-1&3/5
-5&3/5
negative 5 and 3/5(three fifths)
don't forget to mark as brainliest
Answer:
negative 5 and 3/5
Step-by-step explanation:
-4-1&3/5
-5&3/5
negative 5 and 3/5(three fifths)
don't forget to mark as brainliest
Step-by-step explanation:
PLS HELP ME,I AM LOSING MY MIND,I WILL GIVE BRAINLIEST AND 30 POINTS.
Kylie's class is selling boxes of chocolate as a fundraiser. In order to motivate students to sell, her teacher has divided the class into two teams: the blue team and the red team. Since the teams do not have the same number of people, the team with the highest mean sales will win the competition. The dot plots below show the current sales of each team.Calculate the mean and mean absolute deviation (rounded to the nearest tenth) for each team and then complete the following statements.
Currently, the
Choose one of the following: blue or red,team has a higher mean.
The difference between the means is
Choose one of the following:higher or lower, than the mean absolute deviation of either team.
There is
Choose one of the following:no,much,or some, overlap between sales in the teams.

Answers
Answer:
Currently, the RED team has a higher mean.
The difference between the means is HIGHER than the mean absolute deviation of either team.
There is SOME overlap between sales in the teams.
Dominique is allowed to play up to 8 hours of video games this week. They want to play video
games for at least 4 hours this weekend. Which of the following can be used to represent t, the
number of hours they can play video games before the weekend?
8-t>4
8-t < 4
t-8>4
t-8<4
Answers
The number of hours they can play the video games before the weekend, then the inequality that represents the situation will be:
8 - t ≤ 4
What is an Inequality?An inequality is a mathematical statement that compares two quantities or expressions that are not equal using the inequality signs such as:
Greater than: >Less than: <Greater than or equal to: ≥Less than or equal to: ≤We are give that:
Total hours Dominique is allowed to play is 8 hours, this means 8 hours is the maximum number of hours he can play in a week.
Number of hours to be played during for the weekend is given as, at least 4 hours. This means, the number of hours to play at weekend can be 4 hours or more.
If t represents the number of hours they can play the video games before the weekend, then the inequality that represents the situation will be:
8 - t ≤ 4
Learn more about inequality on:
https://brainly.com/question/11613554
#SPJ1
please please help me

Answers
Answer:
x = 6
Step-by-step explanation:
Segment representing 2x - 1 is the mid segment of the given triangle.
Therefore, by mid segment theorem:
2(2x - 3) = 18
2x - 3 = 18/2
2x - 3 = 9
2x = 9 + 3
2x = 12
x = 12/2
x = 6
Answer:
x = 6
Step-by-step explanation:
D is the mid-point of AB (given)
E is the mid-point of AC (given)
Therefore, by mid-point theorem,
DE = 1/2 BC
=> 2x - 3 = 1/2 × 18
=> 2x - 3 = 9
=> 2x = 12
=> x = 6
Hope it helps :)
Please mark my answer as the brainliest

Suppose K⊆Rn is compact, f:K→R is continuous, and ϵ>0. Show that there is a number A>0 such that
|f(x)−f(y)|≤A∥x−y∥+ϵ,∀x,y∈K.
Answers
By using the concept of compact set, it can be proved that
|f(x)−f(y)|≤A∥x−y∥+ϵ,∀x,y∈K.
What is compact set?
A set K is said to be compact if every open cover of K has a finite subcover.
Let K⊆Rn is compact f:K→R is continuous, and ϵ>0
Let there exist \(x_n, y_n\) ∈ K such that |f(\(x_n\))−f(\(y_n\))| > n∥\(x_n\)−\(y_n\)∥+ϵ,
Since K is compact there is a subsequence \(x_{nk}\) and \(y_{nk}\) of \(x_n, y_n\) respectively such that \(x_{nk}\) converges to x and \(y_{nk}\) converges to y.
So, |f(\(x_{nk}\))−f(\(y_{nk}\))| > \(n_k\)∥\(x_{nk}\)−\(y_{nk}\)∥+ϵ,
Since f is continuous,
We can write
|f(x)−f(y)| > \(n_k\)∥x - y∥+ϵ,
This is true for infinite many \(n_k\)
So ||x - y|| = 0
|f(x) - f(y)| > ϵ, a contradiction since f is continuous
So, there is a number A>0 such that
|f(x)−f(y)|≤A∥x−y∥+ϵ,∀x,y∈K.
To learn more about compact set, refer to the link-
https://brainly.com/question/17175854
#SPJ4
If triangle ABC is reflected across the x-axis the coordinates will be:

Answers
The reflected coordinates of triangle ABC across the x-axis are:
A'(2, -4), B'(9, -4), and C'(4, -7).
Coordinate the given triangle ABC as per the given figure is,
A(2, 4), B(9, 4), and C(4, 7)
When a triangle is reflected across the x-axis, the y-coordinates of its vertices are negated while the x-coordinates remain the same.
For the given triangle ABC:
A(2, 4), B(9, 4), and C(4, 7)
If we reflect the triangle across the x-axis, the new coordinates will be:
A'(2, -4)
B'(9, -4)
C'(4, -7)
Learn more about coordinates here:
https://brainly.com/question/20282507
#SPJ1
What is the image point of (1, -3) after a translation right 5 units and up 2 units?
Answers
Answer:(6, -1)
Step-by-step explanation:
Jordyn, Teri, and Morgan are going to have a kite-flying contest. Jordyn and Teri each have one roll of kite string. They also each have yards of extra string. Morgan has three rolls of kite string plus yards of extra string. All of the rolls of string are the same length. The girls want to see who can fly their kite the highest.
a. Since Jordyn and Teri have fewer rolls of kite string, they decide to tie their string together so their kite can fly higher. Write at least two expressions to show how much kite string Jordyn and Teri have. Let x represent the number of yards of string on one roll.
b. Write an expression to show how much kite string Morgan has. Again, let x be the number of yards of string on one roll.
c. How long does a roll of string have to be for Jordyn and Teri to be able to fly their kite higher than Morgan's kite? Show your answer as an inequality and on a number line.
d. How long does a roll of string have to be for Morgan to be able to fly her kite higher than Jordyn and Teri's kite? Show your answer as an inequality and on a number line.
e. What length would the roll of string have to be for the girls' kites to fly at the same height?
Answers
a. The expressions to show how much kite string Jordyn and Teri have, respectively, are 2x + y and x + y
b. The expression to show how much kite string Morgan has is 3x + y
c. The inequality representing is x > 3x + y.
d. The inequality representing is 3x + y > 2x + y.
e. For the girls' kites to fly at the same height, the length of a roll of string (x) would need to be equal for both Jordyn and Teri and Morgan. Therefore, x = 2x + y = 3x + y.
a. Jordyn and Teri each have one roll of kite string, so their expressions would be 2x + y (representing Jordyn's string) and x + y (representing Teri's string). The variable x represents the number of yards of string on one roll, and y represents the yards of extra string they have.
b. Morgan has three rolls of kite string plus extra string. Hence, the expression representing the amount of kite string Morgan has is 3x + y, where x represents the number of yards of string on one roll, and y represents the yards of extra string she has.
c. To fly their kite higher than Morgan's, the combined string length of Jordyn and Teri (2x + y) should be greater than the string length of Morgan (3x + y). This can be represented as the inequality x > 3x + y.
d. For Morgan to fly her kite higher than Jordyn and Teri's, the string length she has (3x + y) should be greater than the combined string length of Jordyn and Teri (2x + y). This can be represented as the inequality 3x + y > 2x + y.
e. For the girls' kites to fly at the same height, the length of a roll of string (x) should be equal for both Jordyn and Teri and Morgan. This means that the expressions 2x + y and 3x + y should be equal. Therefore, x = 2x + y = 3x + y.
Learn more about height here:
https://brainly.com/question/32560368
#SPJ11
Ken puts 4 fluid ounces of bubble mix into each bowl. How many bowls can he fill with 1 pint of bubble mix?
Answers
Answer:
4 bowls
Step-by-step explanation:
Conversion rate :
1 liquid pint = 16 fluid ounces
From the question, we are told that :
4 fluid ounces of bubble mix = 1 bowl
16 fluid ounces of bubble mix(1 liquid pint) = y bowl
Cross Multiply
4 fluid ounces × y bowl = 16 fluid ounces × 1bowl
y bowl = 16 fluid ounces × 1bowl/4 fluid ounces
= 4 bowls
Therefore, he can fill 4 bowls with 1 pint of bubble mix
Calculate the length of AC, to the nearest tenth of a centimeter.

Answers
Answer:
AC ≈ 11.0 cm
Step-by-step explanation:
Using Pythagoras' identity in Δ CDE and Δ ADE
CE² + DE² = DC²
CE² + 7² = 8²
CE² + 49 = 64 ( subtract 49 from both sides )
CE² = 15 ( take the square root of both sides )
CE = \(\sqrt{15}\)
-------------------------------------------------------
AE² + DE² = DA²
AE² + 7² = 10²
AE² + 49 = 100 ( subtract 49 from both sides )
AE² = 51 ( take the square root of both sides )
AE = \(\sqrt{51}\)
Then
AC = AE + CE = \(\sqrt{15}\) + \(\sqrt{51}\) ≈ 11.0 cm ( to the nearest tenth )
Please help! Will give Brainliest!
Identify the axis of symmetry of y = ( x - 7 ) ( x + 1 )
Answers
Please mark brainlyest...!
Factor each expression by finding the GCF.
8 + 16 =
8 ( 1 + 16)
2 (4 + 16)
8 ( 1 + 2)
4 (2 + 6)