How many turns must an ideal solenoid 10 cm long have if it is to generate a magnetic field of 1.5 mT when a current of 1.0 A passes through it?
a) 3.5
b) 1.8
c) 2.2
d) 0.50
e) 2.8
Answers
1.8 turns must an ideal solenoid should have if it is to generate a magnetic field of 1.5 mT when a current of 1.0 A passes through it
To calculate the number of turns required for an ideal solenoid, we can use the formula for the magnetic field inside a solenoid: B = μ₀ * n * I, where B is the magnetic field, μ₀ is the permeability of free space (constant), n is the number of turns per unit length, and I is the current.
Rearranging the formula, we have n = B / (μ₀ * I).
Given B = 1.5 mT (or 1.5 x 10⁻³ T) and I = 1.0 A, and knowing that μ₀ is a constant, we can substitute these values into the formula to find n.
n = (1.5 x 10⁻³) / (4π x 10⁻⁷ * 1.0) ≈ 1.19 x 10⁴ turns/m.
Since the solenoid is 10 cm (0.1 m) long, we can multiply n by the length to find the total number of turns:
Total turns = (1.19 x 10⁴ turns/m) * 0.1 m ≈ 1.19 x 10³ turns.
Rounding to the nearest whole number, the closest option is (b) 1.8.
Learn more about Magnetic Field:
https://brainly.com/question/31838837
#SPJ4
Related Questions
What is the equivalent ratio to 14:10 ?
?:30
Answers
Answer:
42:30
Step-by-step explanation:
10 x 3 = 30
14 x 3 = 42
10 is 3 times to get to 30
So 3 times 14 gets to ?
14:10
42:30
Solving 8 problems per Minute, Fast Funn can finish his test in time. He was, however, working fast, solving 10 problems per minute. That is why he finished 6 minutes early. How many problems were on the text
Answers
The number of problems that were on the text was 240 problems.
What is an equation?An equation is an expression that shows the relationship between two or more variables and numbers.
Let x represent the total number of problems that were on the text, y represent the time to be spent, hence:
y = x/8
Also:
y - 6 = x/10
x/8 - 6 = x/10
x = 240
The number of problems that were on the text was 240 problems.
Find out more on equation at: https://brainly.com/question/13763238
#SPJ1
The area of the parallelogram is 5 times
the area of the triangle and its perpendicular
height is h cm.
Find the value of h.
The triangle is 7cm across and 24cm up and the parallelogram is 30cm across
Answers
Answer:
14 cm
Step-by-step explanation:
Given that:
Base, b of triangle = 5 cm
Height, H of triangle = 24 cm
Base of parallelogram, a = 30 cm
Area of triangle = 0.5 * bH
Area of parallelogram = a * h
Where, h = height of parallelogram
Area of parallelogram is 5 times the area of triangle ;
5 * 0.5 * 7 * 24 = 30 * h
420 = 30* h
h = 420 / 30
h = 14 cm
A rectangular slab on grade is 60 ft 0 in. long × 45 ft 0 in. wide. What is the diagonal measurement in feet and inches?
A. 52 ft 6 in.
B. 75 ft 0 in.
C. 105 ft 8 in.
D. 115 ft 11 in.
Answers
The diagonal measurement as √5625 ft, which is approximately 75 feet, the correct answer is B. 75 ft 0 in.
The diagonal measurement of the rectangular slab on grade can be found using the Pythagorean theorem. The diagonal is the hypotenuse of a right triangle formed by the length and width of the slab.
To calculate the diagonal measurement, we can apply the Pythagorean theorem:
Diagonal² = Length² + Width²
Substituting the given values, we have:
Diagonal² = (60 ft 0 in.)² + (45 ft 0 in.)²
Calculating this expression, we find:
Diagonal² = 3600 ft² + 2025 ft²
Diagonal² = 5625 ft²
Taking the square root of both sides, we obtain:
Diagonal = √5625 ft
Diagonal ≈ 75 ft
Therefore, the diagonal measurement of the rectangular slab on grade is approximately 75 feet.
To find the diagonal measurement of the rectangular slab on grade, we can use the Pythagorean theorem,
which states that in a right triangle, the square of the length of the hypotenuse (diagonal) is equal to the sum of the squares of the other two sides (length and width).
To know more about length click here
brainly.com/question/30625256
#SPJ11
Solve for w.
14 + 3(–w + 6) = –11w
w =
Answers
Answer:
w = -4
Step-by-step explanation:
→Distribute the 3 to (-w + 6):
14 + 3(-w + 6) = -11w
14 -3w + 18 = -11w
→Add like terms:
-3w + 32 = -11w
→Add 11w to both sides:
8w + 32 = 0
→Subtract 32 from both sides:
8w = -32
→Divide both sides by 8
w = -4
Answer:
w= -4
work:
14-3w+18=-11w
32-3w=-11
-3w+11w=-32
8w=-32 divide by 8 then you will get your answer
w=-4
All the pupils at a primary school come from one of three villages: Elmswell, Haughley or Woolpit. 1/4 of the pupils come from Elmswell. 3/5 of the pupils come from Haughley. 102 pupils come from Woolpit. How many pupils are there in total at the school?
Answers
Answer:
680
Step-by-step explanation:
Given that:
All the pupils at a primary school come from one of three villages: Elmswell, Haughley or Woolpit.
\(\frac{1}{4}\) of the pupils come from Elmswell
\(\frac{3}{5}\) of the pupils come from Haughley
102 pupils come from Woolpit.
To find:
Total number of pupils in the school.
Solution:
Let total number of pupils = \(100x\)
So, number of pupils that come from Elmswell = \(\frac{1}{4}\) of 100x
OR
\(\dfrac{1}{4} \times 100x\\\Rightarrow 25x\)
And, number of pupils that come from Haughley= \(\frac{3}{5}\) of 100x
OR
\(\dfrac{3}{5} \times 100x\\\Rightarrow 60x\)
Number of pupils that come from Woolpit = \(100x - 25x - 60x \Rightarrow 15x\)
As per given statement:
\(15x = 102\\\Rightarrow x =6.8\)
Number of pupils from Elmswell = 25x = 25 \(\times\) 6.8 = 170
Number of pupils from Haughley = 60x = 60 \(\times\) 6.8 = 408
Total number of pupils at the school = \(100x \Rightarrow 100 \times 6.8=680\)
Which shows the following expression after the negative exponents have been eliminated?
StartFraction m Superscript 7 Baseline n cubed Over m n Superscript negative 1 Baseline EndFraction, m not-equals 0, n not-equals 0
StartFraction m Superscript 7 Baseline n cubed n Over m EndFraction
m Superscript 7 Baseline n cubed m n
StartFraction m Superscript 7 Baseline n cubed Over m (negative n) EndFraction
StartFraction m n Over m Superscript 7 baseline n EndFraction
Answers
The following expression shows the main expression after the negative exponents have been eliminated: A. m⁷n³n/m.
What is an exponent?In Mathematics, an exponent can be defined as a mathematical operation that is used in conjunction with an algebraic expression to raise a quantity to the power of another and it is generally written as bⁿ.
By applying the property of exponents based on the law of indices for the division of powers, we have the following:
b⁻ⁿ = 1/bⁿ
In this context, the exponent n⁻¹ in the given algebraic expression would be rewritten based on the law of indices for the division of powers as follows;
n⁻¹ = 1/n
Substituting the given parameters into the given algebraic expression, we have the following;
(m⁷n³)/mn⁻¹ = (m⁷n³)/m × n
(m⁷n³)/m × n = (m⁷n³n)/m
(m⁷n³)/mn⁻¹ = m⁷n³n/m
Read more on exponent here: https://brainly.com/question/9524319
#SPJ1

Answer:
Step-by-step explanation:
its A
What is the total surface area?? PLEASE HELP ME

Answers
Answer:
Did I see this quesiton before..?
Step-by-step explanation:
Solve 7(1 – x) + 2 = -19 by interpreting the expression in parentheses as a single quantity. x =
Answers
For approximately what values of x can you replace sin x by x − x^3/6 with an error of magnitude no greater than 6×10^−4?
Answers
With an error of magnitude no more than 6×10^−4, the values of x for which sin x can be replaced by x - x^3/6 are roughly: -0.3728 ≤ x ≤ 0.3728
To find the values of x for which sin x can be replaced by x - x^3/6 with an error of magnitude no greater than 6×10^−4, we need to analyze the Taylor series expansion of sin x around x = 0. The Taylor series for sin x is:
sin x = x - x^3/6 + x^5/120 - x^7/5040 + ...
We are given the approximation sin x ≈ x - x^3/6, which corresponds to the first two non-zero terms of the Taylor series. To find the error bounds, we consider the next term in the series, x^5/120. To have an error no greater than 6×10^−4, we need:
|x^5/120| ≤ 6×10^−4
Now, solve for x:
|x^5| ≤ 72×10^−4
|x| ≤ (72×10^−4)^(1/5)
Calculating the fifth root gives:
|x| ≤ 0.3728
Therefore, the values of x for which sin x can be replaced by x - x^3/6 with an error of magnitude no greater than 6×10^−4 are approximately:
-0.3728 ≤ x ≤ 0.3728
Learn more about "sin x": https://brainly.com/question/15287659
#SPJ11
It’s two parts help meeee please
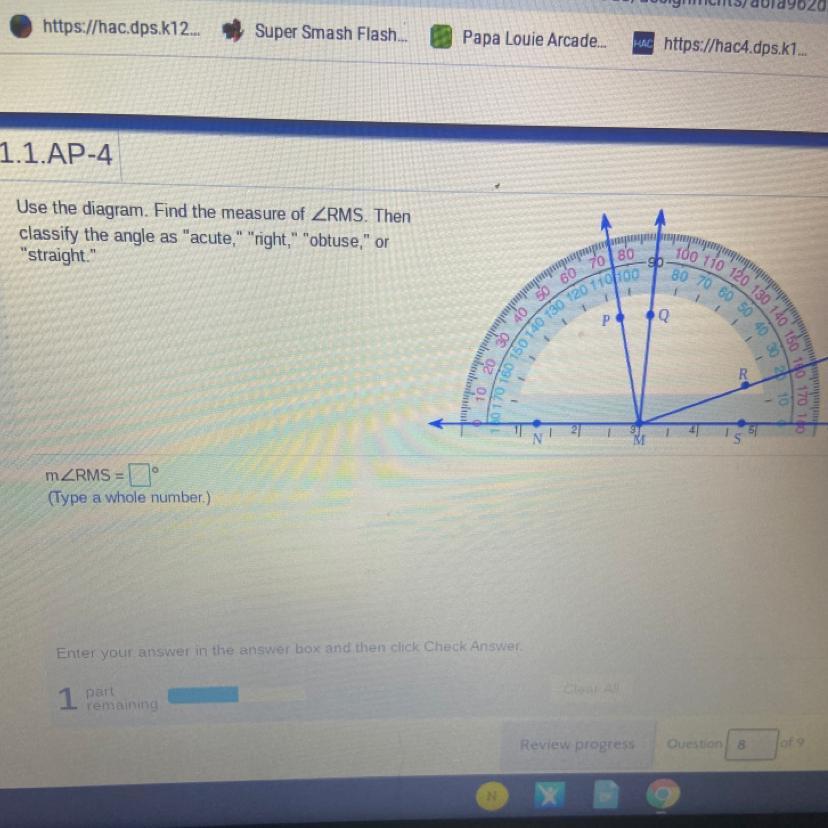
Answers
Answer:
m∠RMS = 20°
Step-by-step explanation:
Find ∠RMS and look at the two values it crosses.
∠RMS crosses through 180 and 160.
Find the difference between the two values to get the measure:
180 - 160 = 20°
So, m∠RMS = 20°
(Its also an acute angle.)
Answer:
20
Step-by-step explanation:
The mistake is in using 160 as the answer. It isn't.
The angle is very small well under 90. It is acute.
The horizontal part of the angle is on 180 degrees of the protractor.
Therefore the angle size is 180 - 160 = 20 degrees.
3. When the graph of a line crosses above the origin, the
y-intercept is
Answers
Hi!
The y-intercept is the place where the line crosses the y-axis.
-------------------------------------------------------------------------------------------------------------
All points directly above and to the right of the origin are positive, and all the points directly below and to the left of the origin are negative.
Therefore, if the graph of a line crosses above the origin, the y-intercept is POSITIVE.
bank randomly selected checking account customers and found that of them also had savings accounts at the same bank. a. find the sample proportion of checking account customers also having savings accounts, . b. find the standard error of the sample proportion, . c. find a 95% confidence interval for the population proportion of checking account customers who also have savings accounts
Answers
We can say with 95% confidence that the true proportion of checking account customers who also have savings accounts in the population lies between 0.25 and 0.35.
a. To find the sample proportion of checking account customers who also have savings accounts, we need to divide the number of customers who have both types of accounts by the total number of checking account customers in the sample. Let's say the bank selected 500 checking account customers and found that 150 of them also had savings accounts. Then, the sample proportion would be:
150/500 = 0.3
So, 30% of the checking account customers in the sample also had savings accounts.
b. To find the standard error of the sample proportion, we use the formula:
SE = sqrt(p*(1-p)/n)
where p is the sample proportion (0.3 in this case), and n is the sample size (500). Plugging in the numbers, we get:
SE = sqrt(0.3*(1-0.3)/500) = 0.025
So, the standard error is 0.025.
c. To find a 95% confidence interval for the population proportion of checking account customers who also have savings accounts, we use the formula:
CI = p ± z*(SE)
where z is the z-score corresponding to a 95% confidence level (which is 1.96), and SE is the standard error we calculated in part b. Plugging in the numbers, we get:
CI = 0.3 ± 1.96*(0.025) = (0.25, 0.35)
Learn more about standard error here:
brainly.com/question/13179711
#SPJ11
WILL MARK BRAINLIEST IF CORRECT

Answers
Assume, Tane's utility function is: U( W)=W∧0.5 (square root of W ) and he operates under the tenets of expected utility theory. He is considering taking a job with a start-up company that will pay a base salary of $30,000 but offers the potential of a $70,000 bonus at the end of the year with a 0.5 probability. This means that at the end of the year with 0.5 probability he will get $30000 and with 0.5 probability he will get $100000. Tane is not comfortable with this probabilistic salary scheme. He would prefer to accept a job that pays a certain fixed salary. Which of the following statements is CORRECT? Tane will accept any job as long as the job comes with a certain payment of at least $40,000 (approx.). Tane will accept any job as long as the job comes with a certain payment of at least $50,000 (approx.). Tane will not accept any job with a certain payment of less than $80,000 (approx.). Tane will accept any job as long as the job comes with a certain payment of at least $60,000 (approx.).
Answers
As per given utility function, Tane will accept any job as long as the job comes with a certain payment of at least $40,000 (approx.).
Tane's utility function, \(U(W)=W^{0.5}\), indicates that he has a concave utility function, implying diminishing marginal utility of wealth. This means that Tane values each additional dollar of wealth less as his wealth increases.
Considering the job offer with a base salary of $30,000 and a potential $70,000 bonus with a 0.5 probability, we can calculate the expected value of this salary scheme. The expected value is calculated as the sum of each possible outcome multiplied by its respective probability:
Expected Value = (0.5 * $30,000) + (0.5 * $100,000) = $65,000
Since the expected value is less than $80,000 (approx.), which is the minimum certain payment Tane would accept, Tane would not accept the job offer with the probabilistic salary scheme.
However, Tane's utility function indicates that he values certainty in income. As long as the job comes with a certain payment of at least $40,000 (approx.), Tane would prefer to accept the job because the certain payment guarantees a minimum level of income, providing him with a higher level of certainty and potentially higher utility compared to the probabilistic salary scheme. Therefore, Tane will accept any job as long as the job comes with a certain payment of at least $40,000 (approx.).
Learn more about utility function here : https://brainly.com/question/31055643
#SPJ11
help pls, i can’t find the answer. the answer has to be a whole number

Answers
Joy is making a fruit salad. For every 2 cups of blueberries that Joy uses in the fruit salad, she uses 3 cups of strawberries. If Joy wants to use 6 cups of blueberries in the fruit salad, how many cups of strawberries will she need to use? Use Scratchpad to draw a tape diagram to show your work.
Answers
Answer:
Joy will need to use 9 cups of strawberries for 6 cups of blueberries.
Step-by-step explanation:
Given,
Cups of blueberries used for 3 cups of strawberry = 2
Ratio of cups of blueberry to strawberry = 2:3
Joy wants to use 6 cups of blueberries.
Let,
x be the cups of strawberry for 6 cups of blueberries.
Ratio of cups of blueberries to strawberries = 6:x
Using proportion;
Ratio of cups of blueberry to strawberry :: Ratio of cups of blueberries to strawberries
Product of extreme = Product of mean
Dividing both sides by 2
Write the number three-hundred-sixty-five-thousandths in standard form.
Answers
Answer:
365/1,000 or .365
Step-by-step explanation:
HTH :)
Three hundred sixty five thousand in standard form is 365000.
What is standard form and word form of numbers ?The standard form of numbers is when we have to write the number in digits according to it's place and face value.
Word form of numbers is that when we have to write numbers given in numerical form to words by determining place and face value.
According to the given question we have to write three thousand sixty five thousand in standard form.
We know thousand has three zeroes.Suppose we have to write one thousand in standard form which is 1000.
Given we have to write three hundred sixty five thousand in standard form which is 365000.
learn more about numbers here :
https://brainly.com/question/17264364
#SPJ2
will give thumbs up if correct
7. Determine the intervals of increase/decrease for the function f(x) == (5 marks)
Answers
The intervals of increase/decrease for the function f(x) cannot be determined without additional information.
To determine the intervals of increase/decrease for a function, we need to analyze the behavior of its derivative. The derivative of a function gives us information about its slope and whether it is increasing or decreasing.
However, in this question, only the function f(x) is given, and no information about its derivative is provided. Without the derivative, we cannot determine the intervals of increase/decrease for the function.
To find the intervals of increase/decrease, we would need to calculate the derivative of f(x) and analyze its sign changes. A positive derivative indicates the function is increasing, while a negative derivative indicates the function is decreasing. The points where the derivative changes sign represent the boundaries between the intervals.
Without the derivative or any additional information about the behavior of the function, it is not possible to determine the intervals of increase/decrease for f(x).
Learn more about: Intervals
brainly.com/question/30486507
#SPJ11
Mrs Hayes has promised her two teenagers that they may go to a concert if together they save more than $25 of their spending money the older teenager agrees to save twice as much as the younger how much must each save?
Answers
The money saved by the younger teenager will be $8.3 and the money saved by the older teenager will be $16.7.
What is Equation modelling?Equation modelling is a process of creating a mathematical relation from a mathematical word problem keeping in mind the correct use of operations, variables and constants as per need.
Assume that the older teenager is represented by T[O] and the younger teenager by T[Y].
Assume that the money saved by T[Y] is $x.
Then, the money saved by T[O] will be $2x.
The total money to be saved = $25
Then we can write -
x + 2x = 25
3x = 25
x = 8.33
Money saved by T[Y] = $8.3
Then, the money saved by T[O] = $2x = $16.7
Therefore, the money saved by the younger teenager will be $8.3 and the money saved by the older teenager will be $16.7.
To solve more questions on finding unknown variable, visit the link below-
https://brainly.com/question/2361463
#SPJ1
What is distance between -8 and 3 on the number line
Answers
Answer:
11
Step-by-step explanation:
Answer:
11
Step-by-step explanation:
You do -8 - 3 and you get 11
someone help me please i need this by today

Answers
Answer:
In the picture above
Step-by-step explanation:
I solved all questions except no.7 ; I don't know how can be solved.
I hope that its a clear solution. Goodluck

Which of the statements is true for the two equations below?
Equation A: 3(2x-5)=6x-15
Equation B: 2+3x=3x-4
O Equation A has no solution and Equation B has an infinite number of solutions.
O Equation A and Equation B have no solution.
Equation A and Equation B have an infinite number of solutions.
Equation A has an infinite number of solutions and Equation B has no solution
Answers
The statement that is true for the two equations Equation A: 3(2x-5)=6x-15 and Equation B: 2+3x=3x-4 is that "Equation
A has an infinite number of solutions and Equation B has no solution".Explanation:To find the solution for the two equations, we will solve for each equation separately. Solution of equation A: 3(2x - 5) = 6x - 15 ⇒ 6x - 15 = 6x - 15 ⇒ 6x - 6x = -15 + 15 ⇒ 0 = 0
This is a true equation, which means that it is an identity. The equation can be written as 0 = 0. Any value that is inserted in this equation will result in a true statement. Hence the equation A has an infinite number of solutions. Solution of equation B: 2 + 3x = 3x - 4 ⇒ 2 + 4 = 3x - 3x - 4 ⇒ 6 = -4This is a false equation. It means that there is no value that can be inserted into the equation to make it a true statement. Therefore, the equation B has no solution. Hence the statement that is true for the two equations Equation A: 3(2x-5)=6x-15 and Equation B: 2+3x=3x-4 is that "Equation A has an infinite number of solutions and Equation B has no solution".
To know more about prism visit:
https://brainly.com/question/27914026
#SPJ11
Proving parallel lines. Find the value of x so that l // m. State the converse worksheet due tomorrow help please.
Answers
Answer:
x = 17Step-by-step explanation:
Find the diagram attached
The sum of the two adjacent angles is 180 degrees. Hence;
8x-9 + 53 = 180
8x + 44 = 180
Subtract 44 from both sides of the equation
8x + 44 - 44 = 180 - 44
8x = 136
Divide both sides by 8
8x/8 = 136/8
x = 17
Hence the value of x is 17

Part 1 of 5 O Points: 0 of 1 Save The number of successes and the sample size for a simple random sample from a population are given below. x=4, n=200, Hy: p=0.01.H. p>0.01. a=0.05 a. Determine the sample proportion. b. Decide whether using the one-proportion 2-test is appropriate c. If appropriate, use the one-proportion z-lest to perform the specified hypothesis test. Click here to view a table of areas under the standard normal curve for negative values of Click here to view..fable of areas under the standard normal curve for positive values of CALDE a. The sample proportion is (Type an integer or a decimal. Do not round.)
Answers
a. The sample proportion is 0.02.
b. Using the one-proportion z-test is appropriate.
c. Yes, we can use the one-proportion z-test to perform the specified hypothesis test.
a. To determine the sample proportion, we divide the number of successes (x) by the sample size (n). In this case, x = 4 and n = 200. Therefore, the sample proportion is calculated as 4/200 = 0.02.
b. In order to decide whether to use the one-proportion z-test, we need to verify if the conditions for its application are met.
The one-proportion z-test is appropriate when the sampling distribution of the sample proportion can be approximated by a normal distribution, which occurs when both np and n(1-p) are greater than or equal to 10.
Here, np = 200 * 0.01 = 2 and n(1-p) = 200 * (1-0.01) = 198. Since both np and n(1-p) are greater than 10, we can conclude that the conditions for the one-proportion z-test are met.
c. Given that the conditions for the one-proportion z-test are satisfied, we can proceed with performing the hypothesis test.
In this case, the null hypothesis (H0) is that the population proportion (p) is equal to 0.01, and the alternative hypothesis (Ha) is that p is greater than 0.01.
We can use the one-proportion z-test to test this hypothesis by calculating the test statistic, which is given by (sample proportion - hypothesized proportion) / standard error.
The standard error is computed as the square root of (hypothesized proportion * (1 - hypothesized proportion) / sample size).
Once the test statistic is calculated, we can compare it to the critical value corresponding to the chosen significance level (a=0.05) to make a decision.
Learn more about sample proportion
brainly.com/question/11461187
#SPJ11
Suppose a new cross section was created in each solid, both at the same height, using some scale factor k. How would the areas of these 2 cross sections compare? Explain your reasoning.
Answers
The areas of the two cross-sections would be proportional to k².
If a new cross-section was created in each solid, both at the same height using a scale factor k, the areas of the two cross sections would be proportional to k².
The reason for this is that when a scale factor is applied to a two-dimensional figure, the area of the resulting figure increases by a factor of k². This is because the linear dimensions of the figure (length and width) are multiplied by k, and since the area is calculated by multiplying length and width, the area of the figure is multiplied by k².
Therefore, if the two cross sections are created at the same height and are scaled by the same factor k, their areas will be proportional to k². For example, if k=2, the area of each cross-section will be four times the original area; if k=3, the area of each cross-section will be nine times the original area, and so on.
To know more about areas visit:
https://brainly.com/question/27683633?
#SPJ1
(Excel Function)What excel function is used when calculating t critical value?
Answers
The Excel function used when calculating the t critical value is the T.INV function.
The TINV function returns the inverse of the Student's t-distribution, which is a probability distribution that is commonly used in hypothesis testing when the sample size is small and the population standard deviation is unknown. The TINV function requires two arguments: the probability value (alpha) and the degrees of freedom.
The degrees of freedom depend on the sample size and the number of parameters estimated in the model. The TINV function returns the value of the t statistic that corresponds to a given probability and degrees of freedom. This t critical value is compared to the calculated t statistic to determine if the null hypothesis should be rejected or not.
To learn more about Excel, click here:
https://brainly.com/question/29784728
#SPJ11
help me with this question please

Answers
Answer:
N+1
Step-by-step explanation:
It begins with = 2
then n+1=3
then n+2=4 and so on it is n+1
If multiplying by 1 dose not change the value of the number then what effect does multiplying by 2/2 have
Answers
Answer:
The same thing
Step-by-step explanation:
2/2 = 1 so it would have the same effect
let u = 2,−3 , v = −5,1 , and w = −1 2 , 3 2 . compute the following:
u + v =
v + u =
5u =
2u + 3v =
2u + 4w =
u - v + 2w =
|v+ w| =
Answers
The computed values are:
u + v = (-3, -2)
v + u = (-3, -2)
5u = (10, -15)
2u + 3v = (-11, -3)
2u + 4w = (0, 2, 0)
u - v + 2w = (5, 0, 0)
|v + w| = 7.95
Vector addition is the operation of adding two vectors together to obtain a new vector. It is performed by adding the corresponding components of the vectors. For example, if we have two vectors u = \((u_1, u_2, u_3)\) and v = \((v_1, v_2, v_3)\), their sum u + v is given by \((u_1 + v_1, u_2 + v_2, u_3 + v_3)\).
Scalar multiplication is the operation of multiplying a vector by a scalar (a real number). It is performed by multiplying each component of the vector by the scalar. For example, if we have a vector u = \((u_1, u_2, u_3)\) and a scalar k, their product k * u is given by \((k * u_1, k * u_2, k * u_3\)).
Both vector addition and scalar multiplication are fundamental operations in linear algebra and are used to manipulate and combine vectors in various applications.
To compute the given expressions, we perform vector addition and scalar multiplication as follows:
u + v =
\(= (2, -3) + (-5, 1) \\= (2 - 5, -3 + 1) \\= (-3, -2)\)
v + u =
\(=(-5, 1) + (2, -3) \\= (-5 + 2, 1 - 3) \\= (-3, -2)\)
5u =
\(= 5 * (2, -3) \\= (5 * 2, 5 * -3)\\ = (10, -15)\)
2u + 3v =
\(=2 * (2, -3) + 3 * (-5, 1) \\= (4, -6) + (-15, 3)\\ = (4 - 15, -6 + 3) \\= (-11, -3)\)
2u + 4w =
\(= 2 * (2, -3) + 4 * (-1, 2, 3/2) \\= (4, -6) + (-4, 8, 6)\\ = (4 - 4, -6 + 8, -6 + 6)\\ = (0, 2, 0)\)
u - v + 2w =
\(= (2, -3) - (-5, 1) + 2 * (-1, 2, 3/2) \\= (2, -3) + (5, -1) + (-2, 4, 3) \\= (2 + 5 - 2, -3 - 1 + 4, 0 - 3 + 3) \\= (5, 0, 0)\)
|v + w| =
\(= |(-5, 1) + (-1, 2, 3/2)| \\= |(-5 - 1, 1 + 2, 0 + 3/2)| \\= |(-6, 3, 3/2)| \\= \sqrt{((-6)^2 + 3^2 + (3/2)^2)} \\= \sqrt{(36 + 9 + 9/4)} \\= \sqrt{(63.25)} \\= 7.95\)
Therefore, the computed values are:
u + v = (-3, -2)
v + u = (-3, -2)
5u = (10, -15)
2u + 3v = (-11, -3)
2u + 4w = (0, 2, 0)
u - v + 2w = (5, 0, 0)
|v + w| = 7.95
Learn more about vector addition at:
https://brainly.com/question/32548859
#SPJ4