how many outcomes are possible when rolling a number cube and picking a cube from 4 colored cubes
Answers
There are 24 possible outcomes when rolling a number cube and picking a cube from 4 colored cubes.
To determine the number of possible outcomes when rolling a number cube and picking a cube from 4 colored cubes,
we need to multiply the number of outcomes for each event.
For rolling a number cube (assuming it has 6 sides), there are 6 possible outcomes (1, 2, 3, 4, 5, and 6).
For picking a cube from 4 colored cubes, there are 4 possible outcomes (one for each color).
Now, to calculate the total number of outcomes, multiply the outcomes of each event:
6 (number cube outcomes) x 4 (colored cube outcomes) = 24 possible outcomes.
So, there are 24 possible outcomes when rolling a number cube and picking a cube from 4 colored cubes.
for such more question on word problem
https://brainly.com/question/21405634
#SPJ11
There are 24 possible outcomes when rolling a number cube and picking a cube from 4 colored cubes.
When rolling a number cube, there are six possible outcomes (numbers 1-6). When picking a cube from four colored cubes, there are four possible outcomes. Therefore, the total number of possible outcomes is the product of the number of outcomes from each event: 6 x 4 = 24 possible outcomes.
When rolling a number cube, there are 6 possible outcomes (1, 2, 3, 4, 5, or 6), since a standard number cube has 6 faces, each with a different number.
When picking a cube from 4 colored cubes, there are 4 possible outcomes, one for each color.
To find the total number of outcomes when performing both actions, you can multiply the number of outcomes for each individual action:
Total outcomes = outcomes from rolling a number cube × outcomes from picking a colored cube
Total outcomes = 6 × 4
Total outcomes = 24
So, there are 24 possible outcomes when rolling a number cube and picking a cube from 4 colored cubes.
Learn more about outcomes here:
https://brainly.com/question/14356126
#SPJ11
Related Questions
if v1 = (3,7) and v2 = (2,4), then v1 v2 is equal to which of the following
Answers
Answer:
If it is dot product, then 32.
Step-by-step explanation:
3*2+7*4
6+28
32
Last Tuesday was silly hat day at Aaron's school. 64 students wore a silly hat and 36 students did not. What percentage of the students wore a silly hat?
Answers
The percentage of the students who wore a silly hat is 64 %.
What is the percentage?The percentage is defined as a ratio expressed as a fraction of 100.
We have been given that Last Tuesday was a silly hat day at Aaron's school. 64 students wore a silly hats and 36 students did not.
We have to determine the percentage of the students who wore a silly hat
The total number of students = 64 students wore silly hats and 36 students did not.
The total number of students = 64 + 36 = 100
We have to determine the percentage of the students who wore a silly hat
The percentage of the students wore a silly hat = (64/ 100) × 100
The percentage of the students wore a silly hat = 0.64 × 100
The percentage of the students wore a silly hat = 64 %
Thus, the percentage of students who wore silly hats is 64 %.
Learn more about percentage here:
brainly.com/question/24159063
#SPJ1
How many times greater is the perimeter of triangle ABC than that of triangle DEF? (Note: Do NOT include a label or unit in your answer.)

Answers
Answer:
The answer is 4
Step-by-step explanation:
Triangle DEF is a reflection and dilation of Triangle ABC
DF=3 = BC=12
Multiply DF by 4 and you will get 12 (BC)
Round each z-score to the nearest hundredth.A data set has a mean of x = 73 and a standard deviation of 10.8. Find the z-score for each of the following.(a) x = 85 _____(b) x = 95 _____(c) x = 50 _____(d) x = 75 _____
Answers
To determine the z-score of a raw data x, we have the formula below:
\(z=\frac{rawdata-\operatorname{mean}}{sd}\)Based on the question, our mean is 73 and standard deviation is 10.8.
a. x = 85 (raw data is 85)
Let's plug these values to the z formula.
\(z=\frac{85-73}{10.8}=\frac{12}{10.8}\approx1.11\)We subtracted the mean from the raw data first (85 - 73 = 12). Then, we divide the results by 10.8. The result is 1.11.
Hence, equivalent z-score of x = 85 is 1.11.
I'll give brainliest

Answers
Answer:
C=√4^2+100^2=100.08
solve 2x^2 + 8- 1 = 0. Show all work, and explain why you chose the method that you used to solve the problem.
Answers
Step-by-step explanation:
Assuming you mean 2x² + 8x − 1 = 0, this equation isn't factorable, so use quadratic formula.
x = [ -b ± √(b² − 4ac) ] / 2a
x = [ -8 ± √(8² − 4(2)(-1)) ] / 2(2)
x = [ -8 ± √(64 + 8) ] / 4
x = (-8 ± √72) / 4
x = (-8 ± 6√2) / 4
x = (-4 ± 3√2) / 2
Match the solution set given in inequality with the best solution set given in interval notation

Answers
There you go
I hope this help you

Please help me!
A
B
C
D

Answers
Find a solution to the system of equations 

Answers
Answer:
(4, 1 )
Step-by-step explanation:
the solution to a system of equations given graphically is at the point of intersection of the 2 lines.
the lines intersect at (4, 1 )
then the solution is (4, 1 )
Fill in the missing angle measures.The possible answers are 55 degrees and 125 degrees
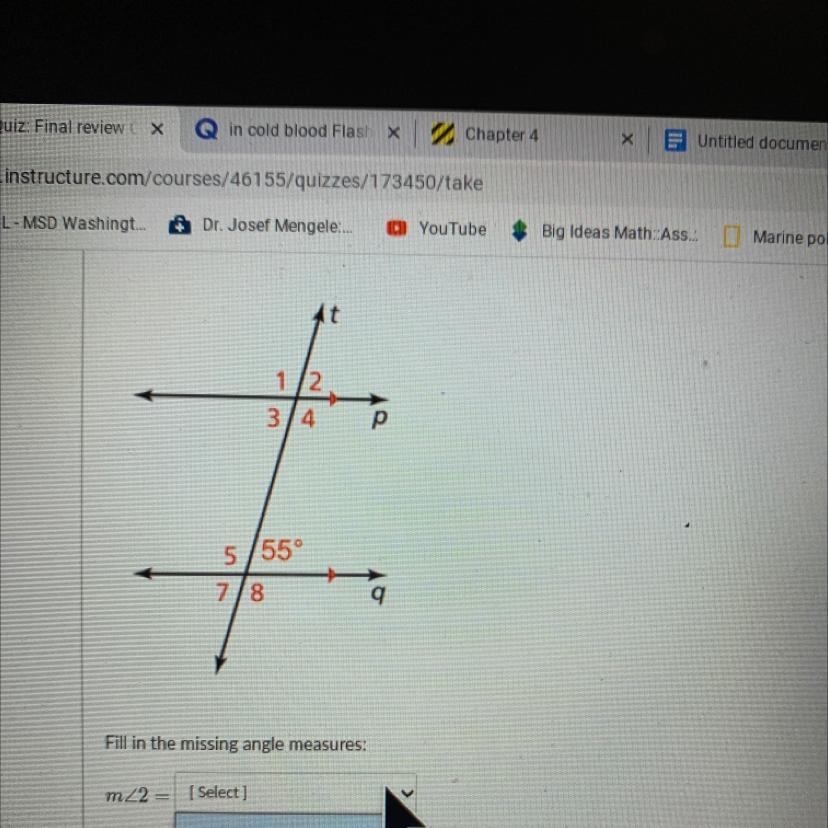
Answers
Since lines p and q are parallel
Since line t intersect them, then
<2 and the angle of measure 55 degrees are corresponding angles
Since the corresponding angles are equal in measures, then
m < 2 = 55 degrees
Since < 2 and < 4 form a pair of linear angles
Since the sum of the measures of the linear angles is 180 degrees, then
m < 2 + m < 4 = 180
55 + m < 4 = 180
Subtract 55 from both sides
55 - 55 + m < 4 = 180 - 55
m < 4 = 125 degrees
Since < 4 and < 5 are alternate angles
Since alternate angles are equal in measures, then
m < 4 = m < 5
m < 5 = 125 degrees
how to solve this? 10x+4y < 12 8x-3y > 20
Answers
Answer: mmm
Step-by-step explanation:
mmm
producto 0 de g(x)=(-5x-1)(2x+8)
Answers
The product of two binomials is the result of multiplying each term from the first binomial by each term from the second binomial. The product of the two binomials, (-5x-1) and (2x+8), is\(0x^2+(-10x-2x)+(-8x-8)\) which simplifies to -18x-10.
To calculate the product of the two binomials, we multiply the coefficients of each term together and add the exponents of the same base together. The coefficients of the first binomial, -5x and -1, are multiplied together to give a coefficient of -5. The exponents of x, 1 and 0, are added together, giving an exponent of 1. Thus, the first term is\(-5x^1\). The coefficients of the second binomial, 2x and 8, are multiplied together to give a coefficient of 16. The exponents of x, 1 and 0, are added together, giving an exponent of 1. Thus, the second term is\(16x^1\).The last terms, -1 and 8, are multiplied together to give a coefficient of -8. The exponents of x, 0 and 0, are added together, giving an exponent of 0. Thus, the third term is\(-8x^0\), which simplifies to -8.When all the terms are combined, the product of the two binomials, (-5x-1) and (2x+8), is -18x-10.
Learn more about binomials here:
https://brainly.com/question/28983916
#SPJ1
Mateo's home is x miles away from school. If Lexi's home is twice as far from school as Mateo's home, which of the following expressions represents the distance between Lexi's home and school, in miles?
Choose 1 answer:
A x − 2
B x + 2
C 2x
D x/2
Answers
Step-by-step explanation:
Mateo home is 2x miles from lexis home and school
Applying the concept of Algebraic expressions, the distance from school to Lexi's home is twice the distance to Mateo's home. Therefore, if Mateo's home is x miles from school, then Lexi's home is 2x miles from school.
Explanation:The question is asking about a comparison between the distances from school to Mateo's and Lexi's homes. The distance from school to Mateo's home is given as x miles. In the question, we know that Lexi's home is twice as far from the school as Mateo's home. Therefore, to express this, we multiply the distance of Mateo's home (x) by 2. This gives us 2x, which is option C from the choices you provided. Hence, the correct expression representing the distance from the school to Lexi's home, in miles, is 2x.
Learn more about Algebraic expressions here:https://brainly.com/question/34192827
#SPJ2
Heart failures are due to either natural occurrences (81%) or outside factors (19%). Outside factors are related to induced substances (73%) or foreign objects (27%). Natural occurrences are caused by arterial blockage (56%), disease (27%), and infection (e.g., staph infection) (17%).
Required:
a. Determine the probability that a failure is due to induced substance.
b. Determine the probability that a failure is due to disease or infection.
Answers
a. The probability that a failure is due to an induced substance is 0.013487 or 1.35% approximately.
b. Probability of a failure due to disease or infection= 44%.
a. Determine the probability that a failure is due to an induced substance.
The total percentage of heart failures that are caused by outside factors is 19%, of which 73% are due to induced substances.
Therefore, the probability that a failure is due to an induced substance = 73/100*19/100= 0.013487 or 1.35% approximately.
b. Determine the probability that a failure is due to disease or infection.
The total percentage of heart failures that are caused by natural occurrences is 81%, of which disease accounts for 27% and infection (e.g., staph infection) accounts for 17%.
Therefore, the probability that a failure is due to disease or infection = 27/100 + 17/100= 0.44 or 44% approximately.
Probability of a failure due to induced substance= 1.35% (approx.)Probability of a failure due to disease or infection= 44% (approx.)
To learn about probability here:
https://brainly.com/question/24756209
#SPJ11
Ella spends $4.25 each day for lunch at school. How much money does she spend on lunches for 5 days?
Answers
Answer:
21.25
Step-by-step explanation:
Answer:
21.25
Step-by-step explanation:
4.25x5=21.25
Combine like-terms of 6x-2x-2=-3x+4(x+7)
Answers
3x-2 = 7x + 28
A team of scientists is traveling by boat to study a pod, or group, of dolphins. The equation y = 0.2x can be used to find the distance, y, in miles the boat travels in x minutes. The dolphins are currently 8.4 mi from the boat. If the dolphins stay to where they are, how long will it take the boat to reach them? Show your work.
Answers
Answer:
42 minutes.
Step-by-step explanation:
We know that:
y = 0.2*x
is the equation that that defines the distance, in miles, that the boat travels in x minutes.
We know that the dolphins are at 8.4 miles from the boat.
Then when we have y = 8.4, this will mean that the boat reached the dolphins.
Then we need to solve the equation:
y = 8.4 = 0.2*x
for x
To do that, we just need to isolate x in one side of the equation, so we can just divide both sides by 0.2 to get:
8.4/0.2 = (0.2*x)/0.2
42 = x
And x is time in minutes, thus, the boat needs to travel for 42 minutes to reach the dolphins.
(Write an equivalent expression by applying the distributive property X+2)(x+9)
Answers
Answer:
Step-by-step explanation:
(x + 2)(x +9)= x*(x +9) + 2*(x +9)
= x*x + x*9 + 2*x + 2*9
= x² + 9x + 2x + 18 {Combine like terms}
= x² + 11x +18
Answer:
x^2 + 11x + 18
Step-by-step explanation:
I assume this is asking about (x+2)(x+9), so if it isn't, then I can't be sure this is right.
That said, the distributive property has to do with multiplication of things in parentheses, meaning you must multiply this expression out to get what the question is asking. When it comes to 2 binomials, you can use the common abbreviation First Inside Outside Last, or FOIL.
Multiply the First terms: x * x = x^2
Multiply the Outside terms: x * 9 = 9x
Multiply the Inside terms: 2 * x = 2x
Multiply the Last terms: 2 * 9 = 18
This leaves you with x^2 + 9x + 2x + 18. Combine your like terms (9x and 2x) to get x^2 + 11x + 18 and you're done!
Somebody help plz I need some help

Answers
Answer:
[C] 44°
Explanation:
That Is A Right Angle, So x° + 46° Needs To Equal 90°Equation: x + 46 = 90
Subtract 46 From Both Sides
x + 46 - 46 = 90 - 46
x = 44
B = 44°C. 44°
Explanation:
maria bought a swimming pool with a circumference of 24 feet. she wants to buy a cover for her pool. what is the approximate size of the cover that maria will need to buy? round your answer to the nearest hundredth.
Answers
The approximate size of the cover that Maria will need to buy is 45. 84 square feet
How to determine the valueThe formula for calculating the circumference of a circle is expressed as;
Circumference = πr²
Where 'r' is the radius of the circle
Now, let's substitute the value of the circumference
24 = 2 × 3. 14 × r
r = 24/6. 28
r = 3. 82 feet
Formula for area = πr²
Substitute value of r
Area = 3. 14 × (3. 82)²
Area = 3. 14 × 14. 59
Area = 45. 84 square feet
Hence, the value is 45. 84 square feet
Learn more about area here:
https://brainly.com/question/25292087
#SPJ1
what is the value of f

Answers
Answer:
f = 22
Step-by-step explanation:
The exterior angle of a triangle is equal to the sum of the 2 opposite interior angles.
140° is an exterior angle of the triangle, thus
4f + 1 + 51 = 140, that is
4f + 52 = 140 ( subtract 52 from both sides )
4f = 88 ( divide both sides by 4 )
f = 22
Given AE and BD bisect each other at point c, which congruence theorem would you use to prove triangle ABC =~ triangle EDC ?

Answers
Explanation:
AC = EC
BC = DC
angle ACB = angle DCE (Vertically Opposite Angles)
Therefore, the triangles are congruent by the Side-Angle-Side congruency
A number has the same digit in its hundreds place and its hundredths place.
How many times greater is the value of the digit in the hundreds place than the
value of the digit in the hundredths place?
11) 100,000
1) 10,000
11) 100
1») 1,000
My Progress
o
Answers
Answer:
10,000
Step-by-step explanation:
100/0.01 is 10k
An election was held between two persons to select a representative to a certain
institution. All the voters who were registered cast their votes. The winner
received 7/12 of the votes and
won by a majority of 120 votes.
(i) What fraction of the total votes did the person who lost receive?
(ii) How many registered voters were there?
(iii) Find the number of votes the winner received.
Answers
9514 1404 393
Answer:
(i) 5/12
(ii) 720
(iii) 420
Step-by-step explanation:
(i) The fraction representing all votes is 12/12. If 7/12 were received by the winner, then the loser received 12/12 -7/12 = 5/12 of the total votes.
The person who lost received 5/12 of the total votes.
__
(ii) The winner won by 7/12 -5/12 = 2/12 = 1/6 of all votes. So, the total number of votes is ...
120 votes = 1/6(total votes)
total votes = 6×120 votes = 720 votes
There were 720 registered voters.
__
(iii) The winner received ...
(7/12)(720 votes) = 420 votes . . . received by the winner
You are filling a 5-L fish tank using a 250-mL container. How many full containers are required to fill the fish tank? PLEASE HELP NOW
Answers
Answer:
20 containers
Step-by-step explanation:
5L = 5000ml
so,
5000/250 = 20 containers
I hope my answer helps you.
fill 5L tank using 250 ml container .
to find:how many full containers are required to fill the tank.
solution:1 L= 1000 mL
1000 mL/250mL = 4
1 L= 4 full containers
4 containers x 5 liters = 20 full containers.
so, 20 full containers are required to fill the fish tank.
At a football stadium, 5% of the fans in attendance were teenagers. If there were 160 teenagers at the football stadium, what was the total number of people at the stadium?
HELP
Answers
Answer:
The total number of people at the stadium was 3200.
Step-by-step explanation:
5% = 160
160 x 20= 3200
Since 20 x 5 is 100, I multiplied 160 by 20 to get 3200.
Find the circumferences of the two circles circle a has a radius of 21 meters and circle b has a radius of 28 meters Is the relationship between the radius of a circle and the distance around the circle the same for all circles
Answers
Answer:
The circumference for circle a is \( \\ C = 131.9430\)m.
The circumference for circle b is \( \\ C = 175.9240\)m.
The relationship between the radius of a circle and the circumference (the distance around the circle) is constant and is the same for all circles and can be written as \( \\ \frac{C}{r} = 2\pi\) or, in a less familiar form, \( \\ \frac{r}{C} = \frac{1}{2\pi}\). The number \( \\ \pi\) is constant for all circles and has infinite digits, \( \\ \pi = 3.14159265358979....\).
Step-by-step explanation:
The circumference of a circle is given by:
\( \\ C = 2*\pi*r\) [1]
Where
\( \\ C\) is the circle's circumference.
\( \\ r\) is the radius of the circle.
And
\( \\ \pi = 3.141592....\) is a constant value (explained below)
We can say that the distance around the circle is the circle's circumference.
The circumferences of the two circles given are:
Circle a, with radius equals to 21 meters (\( \\ r = 21m\)).
Using [1], using four decimals for \( \\ \pi\), we have:
\( \\ C = 2*\pi*r\)
\( \\ C = 2*3.1415*21\)m
\( \\ C = 131.9430\)m
Then, the circumference for circle a is \( \\ C = 131.9430\)m.
Circle b, with radius equals to 28 meters (\( \\ r = 28m\)).
\( \\ C = 2*3.1415*28\)m
\( \\ C = 175.9240\)m
And, the circumference for circle b is \( \\ C = 175.9240\)m.
We know that
\( \\ 2r = D\)
That is, the diameter of the circle is twice its radius.
Then, if we take the distance around the circle and we divided it by \( \\ 2r\)
\( \\ \frac{C}{2r} = \frac{C}{D} = \pi\)
This ratio, that is, the relationship between the distance around the circle (circumference) and the diameter of a circle is \( \\ \pi\) and is constant for all circles. This result is called the \( \\ \pi\) number, which is, approximately, \( \\ \pi = 3.141592653589793238....\) (it has infinite number of digits).
We can observe that the relationship between the radius of a circle and the circumference is also constant:
\( \\ \frac{C}{2r} = \frac{C}{D} = \pi\)
\( \\ \frac{C}{2r} = \pi\)
\( \\ \frac{C}{r} = 2\pi\)
However, this relationship is \( \\ 2\pi\).
We can rewrite it as
\( \\ \frac{r}{C} = \frac{1}{2\pi}\)
And it is also constant.
Answer:
Circle A is 42π
circle C is 56π
The front profile of a shed is depicted in the drawing, with the given dimensions. Find the area of this profile of the shed in square feet.

Answers
Answer:
135 ft²
Step-by-step explanation:
The profile is composed of a triangle and a rectangle.
Area of profile = (area of triangle) + (area of rectangle)
= (½×base×height) + (length × width)
Where,
base of triangle = 15 ft
height of triangle = 11 - 7 = 4 ft
length of rectangle = 15 ft
width of rectangle = 7 ft
Plug in the values
Area of profile = = (½×15×4) + (15×7)
= 30 + 105
Area of profile = 135 ft²
What is the area of the parallelogram?

Answers
Answer:
no se
tep-by-step explanation:
Formula to find area of a parallelogram is BxH.
Area= BxH
Area = (16)x(5)
Area = 80 cm2
For all the values of x,
f(x)=2x^2 and g(x)=x+1
Solve fg(x)=gf(x)
Answers
Answer:
if f(g(x)) = g(f(x)), then x is equal to zero.
Step-by-step explanation:
given:
f(x) = 2x²
g(x) = x + 1
then:
f(g(x)) = 2(x + 1)²
g(f(x) = 2x² + 1
so if:
f(g(x)) = g(f(x))
then:
2(x + 1)² = 2x² + 1
2(x² + 2x + 1) = 2x² + 1
2x² + 2x + 1 = 2x² + 1
2x = 0
x = 0