How many combinations of three high-risk stocks could you randomly select from seven high-risk stocks? Number of ways What is the probability that you would obtain the three highest-returning stocks? (Round your answer to 4 decimal places.) Probability
Answers
Using the combination formula, there are 35 ways to chosen the stock, and a 0.0286 = 2.86% probability that you would obtain the three highest-returning stocks.
The order in which the stocks are chosen is not important, hence the combination formula is used to solve this question.
What is the combination formula?\(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by:
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
In this problem, 3 stocks are taken from a set of 7, hence:
\(C_{7,3} = \frac{7!}{3!4!} = 35\)
Hence the probability that you would obtain the three highest-returning stocks is:
p = 1/35 = 0.0286 = 2.86%.
More can be learned about the combination formula at https://brainly.com/question/25821700
#SPJ1
Related Questions
2. You are in a car traveling an average speed of 60 km/hr. The
total trip is 240 km. How long does the trip take?
Answers
Answer:
4 hours
Step-by-step explanation:
60*4=240
4 x ( 2 + 5 )^2 - 5^2
Answers
=4*49-25
=196-25
=171
PROBLEM I: On Monday the temperature was 70° F. On Tuesday the temperature dropped 10°,
followed by a 5º decrease on Wednesday. On Thursday, the temperature increased 7 degrees followed by a
decrease of 2 degrees on Friday. What was the final temperature on Friday?
Number Sentence:
Solution:
Answers
Answer:
Answer 60 degrees
Step-by-step explanation:
70-10 60-5 55+7 62-2 60
Problem 2. You are looking to purchase a new luxury Dsports car at a price of $93,500. You negotiate a six-year loan, with no money down and no monthly payments during the first year. After the first year, you will pay $1,300 per month for the following five years, with a balloon payment at the end to cover the remaining principal on the loan. The APR on the loan with monthly compounding is 5%. What will be the amount of the balloon payment six years from now?
Answers
So the balloon payment six years from now will be approximately $24,612.09.
What factors determine interest rates?(P, R, and T) / 100 is the SI unit.
In this case, SI stands for Straightforward Interest. P is the initial investment or loan amount, and R is the interest rate.
To find the amount of the balloon payment six years from now, we can use the formula for the present value of a series of payments:
PV = PMT x (1 - (1 + r/n)^(-nt)) / (r/n)
where PV is the present value of the payments, PMT is the monthly payment, r is the annual interest rate (as a decimal), n is the number of times the interest is compounded per year, and t is the total number of years for the loan.
In this case, we have:
PMT = $1,300 (paid for 5 years)
r = 0.05 (5% APR)
n = 12 (monthly compounding)
t = 6 (total loan term, including the first year with no payments)
To calculate the present value of the payments, we first need to find the present value of the $93,500 loan, one year from now, when the payments begin. This is equivalent to finding the future value of the loan now, and then discounting it back one year using the interest rate.
The future value of the loan after one year is:
FV = $93,500 x (1 + r)¹ = $98,175.00
The present value of this future amount, discounted back one year at an interest rate of 5%, is:
PV = $98,175.00 / (1 + r)¹ = $93,500.
So the present value of the loan one year from now, when the payments begin, is approximately $93,500.
Using this present value as the principal amount for the remaining 5 years of payments, we can calculate the balloon payment using the present value formula above:
PV = PMT x (1 - (1 + r/n)^(-nt)) / (r/n)
PV = $1,300 x (1 - (1 + 0.05/12)⁻⁶⁰) / (0.05/12)
PV = $68,887.91
Therefore, the balloon payment six years from now will be the remaining principal on the loan after five years of payments, which is:
Balloon payment = $93,500 - $68,887.91 = $24,612.09.
So the balloon payment six years from now will be approximately $24,612.09.
To know more about interest rate visit:
https://brainly.com/question/13324776
#SPJ1
Find the open intervals on which the function f(x)= x+10sqrt(9-x) is increasing or decreasing.

Answers
The function f(x) = x + 10√(9 - x) is increasing on the interval (-∞, 9) and decreasing on the interval (9, ∞).
To determine the intervals on which the function is increasing or decreasing, we need to find the derivative of the function and analyze its sign.
Let's find the derivative of the function f(x) = x + 10√(9 - x) with respect to x.
f'(x) = 1 + 10 * (1/2) * (9 - x)^(-1/2) * (-1)
= 1 - 5√(9 - x) / √(9 - x)
= 1 - 5 / √(9 - x).
To analyze the sign of the derivative, we need to find the critical points where the derivative is equal to zero or undefined.
Setting f'(x) = 0:
1 - 5 / √(9 - x) = 0
5 / √(9 - x) = 1
(√(9 - x))^2 = 5^2
9 - x = 25
x = 9 - 25
x = -16.
The critical point is x = -16.
We can see that the derivative f'(x) is defined for all x values except x = 9, where the function is not differentiable due to the square root term.
Now, let's analyze the sign of the derivative f'(x) in the intervals (-∞, -16), (-16, 9), and (9, ∞).
For x < -16:
Plugging in a test value, let's say x = -17, into the derivative:
f'(-17) = 1 - 5 / √(9 - (-17))
= 1 - 5 / √(9 + 17)
= 1 - 5 / √26
≈ 1 - 0.97
≈ 0.03.
Since f'(-17) is positive, the function is increasing in the interval (-∞, -16).
For -16 < x < 9:
Plugging in a test value, let's say x = 0, into the derivative:
f'(0) = 1 - 5 / √(9 - 0)
= 1 - 5 / √9
= 1 - 5 / 3
≈ 1 - 1.67
≈ -0.67.
Since f'(0) is negative, the function is decreasing in the interval (-16, 9).
For x > 9:
Plugging in a test value, let's say x = 10, into the derivative:
f'(10) = 1 - 5 / √(9 - 10)
= 1 - 5 / √(-1)
= 1 - 5i,
where i is the imaginary unit.
Since the derivative is not a real number for x > 9, we cannot determine the sign.
Combining the information, we conclude that the function f(x) = x + 10√(9 - x) is increasing on the interval (-∞, 9) and decreasing on the interval (9, ∞).
For more such questions on function, click on:
https://brainly.com/question/11624077
#SPJ8
Find the length of side c.
c=_in

Answers
Answer:
c=9.534
Step-by-step explanation:

Question 6 Which of the following is the graph of f(x) = x² = 5x + 4?
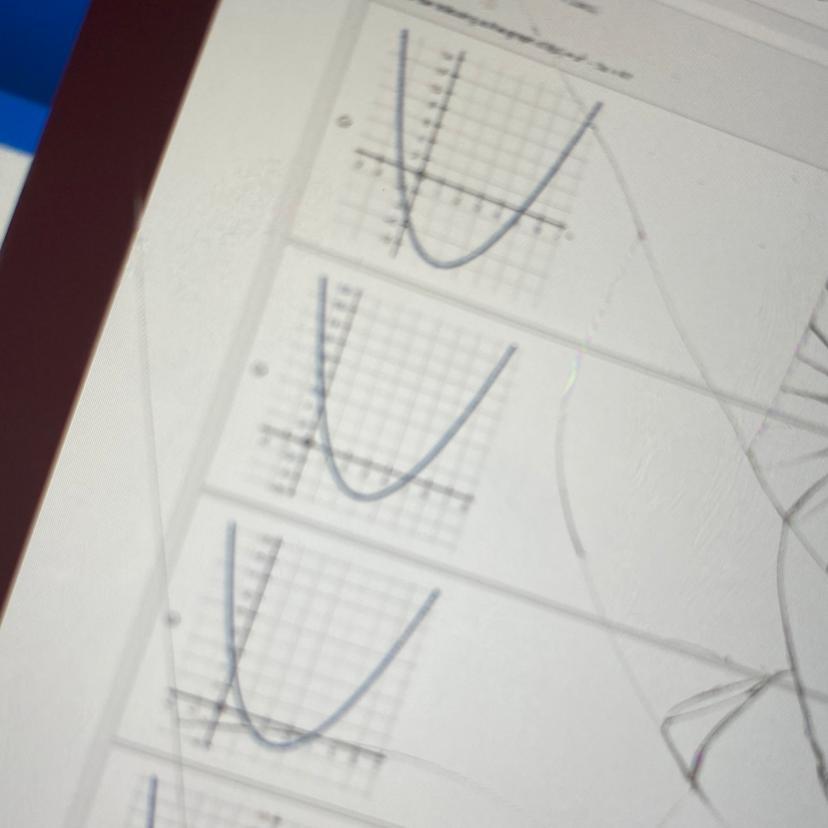
Answers
Given: The equation x² = 5x + 4
We have to draw the the graph for the given equation.
Consider the given equation,
x^2 - 5x - 4 = 0
The vertex of the parabola of the form f(x) = ax^2 + bx + c is given by x = -b/2a
Here,
a= 1
b= -5
c= -4
vertex = x = 5/2= 2.5
Also, the y coordinate at x = 2.5 is,
y = (2.5)^2 -5(2.5)-4
y = -10.25
Thus the vertex of parabola is (2.5 , -10.25)
y - intercept is the point where x = 0
put x = 0 in given equation
f(x) = 0 - 0 -4
f(x) = -4
hence y intercept is at (0, -4).
Now, we calculate x- intercept
x- intercept is where y is equal to 0.
Put f(x) = 0
We have,
x^2 - 5x - 4 = 0
by using quadratic formula,
x = -b ±√b² - 4ac/2a
x=5 ±√-5² - 4 (1)(-4)/2
x= 5±√41/2.
Hence with the obtained values the graph of the equation is obtained.
Learn more about Parabola,
https://brainly.com/question/29267743
#SPJ1
Last season Emily soccer team how to win loss ratio of 9 to 12 and Grant soccer team how to win loss ratio of 10 to 15 who’s team has a higher ratio of wins to losses use complete sentences to explain your reasoning
Answers
The Emily soccer team has the higher ratio of wins to losses.
What is Ratio?Ratio is defined as the relationship between two quantities where it tells how much one quantity is contained in the other.
The ratio of a and b is denoted as a : b.
Given that,
Ratio of win to loss of Emily soccer team = 9 : 12
Ratio of win to loss of Grant soccer team = 10 : 15
9 : 12 = 9 / 12 = (9 × 5) / (12 × 5) = 45 / 60
10 : 15 = 10 / 15 = (10 × 4) / (15 × 4) = 40 / 60
If 60 games are losses, then 45 games are wins for Emily soccer team.
If 60 games are losses, then 40 games are wins for Grant soccer team.
Higher ratio is for Emily soccer team.
Hence higher ratio of wins to losses is for Emily soccer team.
Learn more about Ratios here :
https://brainly.com/question/1706633
#SPJ9
How many degrees are in 11.6pi
Answers
Step-by-step explanation:
\(11.6\pi × \dfrac{180°}{\pi} = 2088°\)
Answer:
11.6 z × 180° / z = 2088°
\(11.6\pi \: \: \: \times \: \: \frac{180}{\pi} = 2088\pi \\ \\ \\ \\ i \: hope \: it \: is \: helpfull\)
Consider the following two loans for P=$5,000. Loan A: 2.5-year loan, annual interest rate of 12%. Loan B: 5-year loan, annual interest rate of 6%. Both loans are paid monthly, and their interest is compounded monthly. Calculate the absolute difference between the total interest paid on both loans. Round your answer to the nearest cent. Do NOT round until you calculate the final answer.
Answers
Answer:
For Loan A:
Number of months: 2.5 x 12 = 30
Monthly interest rate: 12% / 12 = 1%
Monthly payment: Pmt = PV x (r / (1 - (1 + r)^-n))
Pmt = 5000 x (0.01 / (1 - (1 + 0.01)^-30)) = $220.15
Total payment: 220.15 x 30 = $6,604.50
Total interest: 6604.50 - 5000 = $1,604.50
For Loan B:
Number of months: 5 x 12 = 60
Monthly interest rate: 6% / 12 = 0.5%
Monthly payment: Pmt = PV x (r / (1 - (1 + r)^-n))
Pmt = 5000 x (0.005 / (1 - (1 + 0.005)^-60)) = $95.12
Total payment: 95.12 x 60 = $5,707.20
Total interest: 5707.20 - 5000 = $707.20
Absolute difference in total interest: $1,604.50 - $707.20 = $897.30. Therefore, the absolute difference between the total interest paid on both loans is $897.30.
Answer: $12.60
Step-by-step explanation:
First, we must calculate the monthly repayments on both loans, and calculate the interest from there: For Loan A: To calculate the monthly repayments we use
d=P(rn)(1−(1+rn)−n⋅t)
and substituting the relevant values gives
dA=5000(0.1212)(1−(1+0.1212)−12⋅2.5)
which yields dA=$193.74.
The total interest on Loan A is
IA=$193.74×12×2.5−$5,000=$812.20.
For Loan B: To calculate the monthly repayments we use
d=P(rn)(1−(1+rn)−n⋅t)
and substituting the relevant values gives
dB=5000(0.0612)(1−(1+0.0612)−12⋅5)
which yields dB=$96.66. The total interest on Loan B is
IB=$96.66×12×5−$5,000≈$799.60,
and therefore the absolute difference between the two is
|IA−IB|=$12.60.
Each triangle in the net has a base length that measures 6 inches and a height that measures 4 inches. What is the surface area of the pyramid that can be formed from this net? 12 inches squared 24 inches squared 36 inches squared 48 inches square
Answers
Answer:
Surface area of triangular pyramid = 48 inch²
Step-by-step explanation:
Given:
Base length of triangle = 6 inches
Height of triangle = 4 inches
Find:
Surface area of triangular pyramid
Computation:
Surface area of triangular pyramid = 4 x [Surface area of triangle]
Surface area of triangular pyramid = 4 x [(1/2)(b)(h)
Surface area of triangular pyramid = 4 x [(1/2)(6)(4)
Surface area of triangular pyramid = 4 x [(1/2)(24)]
Surface area of triangular pyramid = 4 x 12
Surface area of triangular pyramid = 48 inch²
I need help with this

Answers
Answer:
1500
Step-by-step explanation:
Number of boxes = 12
Number of pencils in each box = 125
Total number of pencils
= 12 × 125
= 1500 pencils
Perpendicular line from a 90 angle
True or false
Answers
Show your work and explain in full sentence how 4 2/6 is equivalent to 3 8/6.
Answers
Answer:
Step-by-step explanation:
The given fractions that we are comparing are expressed as mixed numbers. It means that each is made up of whole numbers and fractions. We would convert each mixed number to improper fraction. By converting to improper fraction, we would multiply the whole number by the denominator and add the product to the numerator. The fraction would be the ratio of the result to the denominator.
Considering 4 2/6, it becomes
(4 × 6) + 2) = 26/6
Considering 3 8/6, it becomes
(3 × 6) + 8)/6 = 26/6
Therefore, they are equivalent
Cost of goldfish: $3.45
Markup: 29%
What is the new cost?
Answers
After the markup in the price, the new cost of goldfish will be equal to $4.45.
What is the Percentage?The Latin phrase "per centum," which means "by the hundred," is where the English word "percentage" comes from. Percentage segments are those with a numerator of 100. In other words, it is a connection where the whole is always deemed to be valued 100.
As per the given information in the question,
Cost of goldfish = $3.45
Markup = 29%
So, the price increase will be,
(3.45 × 29)/100
= 100.05/100
= 1.0005
So, the new price is,
$3.45 + $1.0005
= $4.4505 ≈ $4.45
To know more about Percentage:
https://brainly.com/question/29306119
#SPJ1
10(-2.5)(-4) what is the answer plz explain
Answers
Answer:
100
Step-by-step explanation:
10(-2.5) = -25 since negative times positive is negative.
-25(-4)=100 since negative times negative is positive.
Basically, the negative inverts the sign so a negative negates a positive yielding a negative while a negative negates a negative yielding a positive.
Think of it as not not vs not
Figure A is similar to Figure B. What must always be true?
a.
The corresponding side lengths of A and B are proportional.
c.
The corresponding side lengths of A and B are equal.
b.
The corresponding side lengths of A are twice the corresponding side lengths of B.
d.
The corresponding side lengths of A are half the corresponding side lengths of B.
Answers
Option (a) is the correct answer. When two figures are similar, it means they have the same shape but different sizes.
How to solve the question?
In other words, their corresponding angles are congruent, and their corresponding side lengths are proportional.
Option (b) and (d) suggest that the corresponding side lengths of A and B are related by a constant factor (either 2 or 1/2). However, this is not necessarily true for all similar figures. The constant of proportionality can be any positive real number.
Option (c) suggests that the corresponding side lengths of A and B are equal, which means that A and B are not just similar but congruent. This is not necessarily true for all similar figures, as similar figures can differ in size.
Therefore, option (a) is the only answer that must always be true for similar figures. The corresponding side lengths of similar figures are proportional, which means that if one side of figure A is twice as long as a corresponding side of figure B, then all other corresponding sides will also be in the same ratio of 2:1. Similarly, if one side of figure A is three times as long as a corresponding side of figure B, then all other corresponding sides will also be in the same ratio of 3:1. This proportional relationship holds true for all pairs of corresponding sides in similar figures
To know more about similar visit :-
https://brainly.com/question/14285697
#SPJ1

Option (a) is the correct answer. The corresponding side lengths of A and B are proportional, must always be true if Figure A is similar to Figure B.
How to find if the figure is similar?When two figures are similar, their corresponding angles are congruent, and their corresponding side lengths are proportional. This means that if we take any two corresponding sides of the figures, the ratio of their lengths will be the same for all pairs of corresponding sides.
Option b and d cannot be true, as they both suggest a specific ratio of corresponding side lengths, which is not necessarily true for all similar figures.
Option c is not necessarily true, as two similar figures can have corresponding side lengths that are not equal but still have the same ratio.
To know more about similar visit :-
brainly.com/question/14285697
#SPJ1
which are pairs of perpendicular lines?

Answers
Answer:
D
Step-by-step explanation:
The product of the slope of perpendicular lines = -1
y = (-1/4)x - 6 ; here slope = -1/4
y = 4x + 11 ; slope = 4
\(4 * \frac{-1}{4}=-1\)
Please help: At 12.4% interest rate compounded annually money in savings will double in five years.
True
False
Answers
At 12.4% interest rate compounded annually money in savings will double in five years; true.
What is the interest ?Interest is the cost of borrowing money, or the amount that you get when you lend money. It is typically expressed as a percentage of the amount borrowed or lent. The interest rate is determined by the lender and is based on a variety of factors, including the amount being borrowed, the credit score of the borrower, and the amount of time for which the money is borrowed or lent. Interest is usually paid over a period of time and is usually compounded, meaning that interest is added to the principal amount and the total amount owing grows.
To learn more about interest
https://brainly.com/question/25793394
#SPJ1
Please help. Dont put a random answer plz.

Answers
Answer:
Explination:
Work:
A can of apple juice contains 175 calories per 2.5 servings at this rate how many calories are in 4 servings
Answers
Which steps can be used to solve for the value of y?
2/3 (y+57)=178
A. Divide both sides by 2/3, then subtract 57 from both sides.
B. Subtract 57 from both sides, then divide both sides by 2/3.
C. Multiply both sides by 2/3, then subtract 57 from both sides.
D. Subtract 2/3 from both sides, then subtract 57 from both sides.
Answers
Answer:
A. Divide both sides by 2/3, then subtract 57 from both sides.
Step-by-step explanation:
You want to know the steps to solve 2/3(y +57) = 178 for y.
StepsThe variable has 57 added to it, and the sum is multiplied by 2/3. To solve for y, you need to undo these operations in reverse order.
First, you divide by 2/3.
y +57 = 267
Then you subtract 57.
y = 210
( 70 POINTS!! ) In a survey of 2837 adults, 1436 say they have started paying bills online in the last year.
Construct a 99% confidence interval for the population proportion. Interpret the results.
Question
Part 1
A 99% confidence interval for the population proportion is =( ? , ? )
.
(Round to three decimal places as needed.)
Part 2
Interpret your results. Choose the correct answer below.
A. With 99% confidence, it can be said that the sample proportion of adults who say they have started paying bills online in the last year is between the endpoints of the given confidence interval.
B. The endpoints of the given confidence interval show that adults pay bills online 99% of the time.
C. With 99% confidence, it can be said that the population proportion of adults who say they have started paying bills online in the last year is between the endpoints of the given confidence interval.
Answers
The correct answer is Part 1: The 99% confidence interval for the population proportion is approximately (0.4716, 0.5416).Part 2: With 99% confidence, the population proportion of adults who say they have started paying bills online in the last year is between the endpoints of the given confidence interval.
Part 1:
To construct a 99% confidence interval for the population proportion, we can use the formula:
Confidence Interval = Sample Proportion ± Margin of Error
where the margin of error is determined by the level of confidence and the standard error.
First, let's calculate the sample proportion:
Sample Proportion = (Number of adults who say they have started paying bills online) / (Total number of adults surveyed)
Sample Proportion = 1436 / 2837 ≈ 0.5066 (rounded to four decimal places)
Next, we need to calculate the standard statistics error, which is the measure of the variability in the sample proportion:
Standard Error = sqrt((Sample Proportion * (1 - Sample Proportion)) / Sample Size)
Standard Error = sqrt((0.5066 * (1 - 0.5066)) / 2837) ≈ 0.0136 (rounded to four decimal places)
Now, we can calculate the margin of error:
Margin of Error = Critical Value * Standard Error
The critical value is based on the desired confidence level. For a 99% confidence level, the critical value is approximately 2.576 (obtained from a standard normal distribution table).
Margin of Error = 2.576 * 0.0136 ≈ 0.0350 (rounded to four decimal places)
Finally, we can construct the confidence interval:
Confidence Interval = Sample Proportion ± Margin of Error
Confidence Interval = 0.5066 ± 0.0350
Confidence Interval ≈ (0.4716, 0.5416) (rounded to four decimal places)
Part 2:
The correct interpretation is:
C. With 99% confidence, it can be said that the population proportion of adults who say they have started paying bills online in the last year is between the endpoints of the given confidence interval.
This means that we are 99% confident that the true proportion of adults who have started paying bills online falls within the range of 0.4716 to 0.5416. The survey results suggest that approximately 47.16% to 54.16% of the population of adults have started paying bills online in the last year.
Learn more about statistics here:
https://brainly.com/question/15525560
#SPJ8
Jaelyn uses 3 3/4 cups of flour to make 5 batches of pancakes. How many cups of flour she need to make 1 batch?
NO ANSWERS IN UNKNOWN SITES PLEASE OR I'LL REPORT IT!!!
Answers
Answer:
3/4
Step-by-step explanation:
Divide 3 3/4 by 5. 3 3/4 as an improper fraction is 15/4. 15/4 * 1/5 (divided by 5) is 3/4. :D dont report me
Mary drove at a constant speed of 60 miles per hour. How far would she travel if she drove for 4 hours?
Answers
Answer:
4x60=240 Answer is 240
Step-by-step explanation
240
STUCK AGAIN PLEASE HELP !
-18,762=-3z-540
Answers
Answer:
z = 6074
Step-by-step explanation:
-18762 = -3z - 540
-3z = -18762 + 540
-3z = -18,222
z = 6074
Answer:
Your answer is: ↓
Step-by-step explanation:
Hope this helped : )

help please this is important

Answers
Answer:
D. \(3^3 - 4^2\)
Step-by-step explanation:
Well if Alia gets 4 squared less than Kelly who get 3 cubed it’s natural the expression is 3^3 - 4 ^2
Give the domain and range of each of the following functions.

Answers
The range of f(x) is (-∞,0) U (0,∞) and the range of g(x) is [-1,1].
what is function?
In mathematics, a function is a relationship between two sets of elements, called the domain and the range, such that each element in the domain is associated with a unique element in the range. In simpler terms, a function is a set of rules that takes an input value and produces a corresponding output value.
A. The domain of f(x) is all real numbers except x = 0 and x = 9, because the denominator cannot be equal to zero. Therefore, the domain of f(x) is (-∞,0) U (0,9) U (9,∞). To find the range, we can analyze the behavior of the function as x approaches infinity and negative infinity. As x approaches infinity or negative infinity, the function approaches 0. Therefore, the range of f(x) is (-∞,0) U (0,∞).
B. The domain of g(x) is all real numbers except x = 3 and x = -3, because the denominator cannot be equal to zero. Therefore, the domain of g(x) is (-∞,-3) U (-3,3) U (3,∞). To find the range, we can analyze the behavior of the function as x approaches infinity and negative infinity. As x approaches infinity or negative infinity, the function approaches -1 and 1, respectively. Therefore, the range of g(x) is [-1,1].
To learn more about functions from the given link:
https://brainly.com/question/12431044
#SPJ1
A cylinder has a volume of 1 and one third in3 and a radius of one third in. What is the height of a cylinder? Approximate using pi equals 22 over 7.
42 over 6 inches
42 over 9 inches
42 over 11 inches
42 over 22 inches
Answers
The height of the cylinder is approximately 42/11 inches. The answer is option C.
What is the formula for the volume of the cylinder?
The formula for the volume of a cylinder is V = πr²h, where V is the volume, r is the radius, and h is the height.
We are given that the volume of the cylinder is 1 and one-third in^3 and the radius is one-third in. Substituting these values into the formula, we get:
1 and one-third = 4/3
V = π(1/3)²h = 4/3
Simplifying the equation, we get:
h = (4/3) / (π(1/3)²) = (4/3) / (π/9) = (4/3) * (9/π) = 12/π
Approximating π as 22/7, we get:
h ≈ (12/π) ≈ (12/(22/7)) = 42/11 inches
Therefore, the height of the cylinder is approximately 42/11 inches. The answer is option C.
To learn more about the volume of the cylinder visit:
https://brainly.com/question/6204273
#SPJ1
70 points! Please answer fast!

Answers
Answer:
slope = 2
Step-by-step explanation:
will make it so simple and short
slope = rise / run
slope = 6 / 3
slope = 2
Answer:
B
Step-by-step explanation:
The formula for slope is (y2-y1)/(x2-x1)
In this case it is (1+5)/(3-0)
6/3
2