How I can answer this question, NO LINKS, if you answer correctly I will give u brainliest!

Answers
Answer:
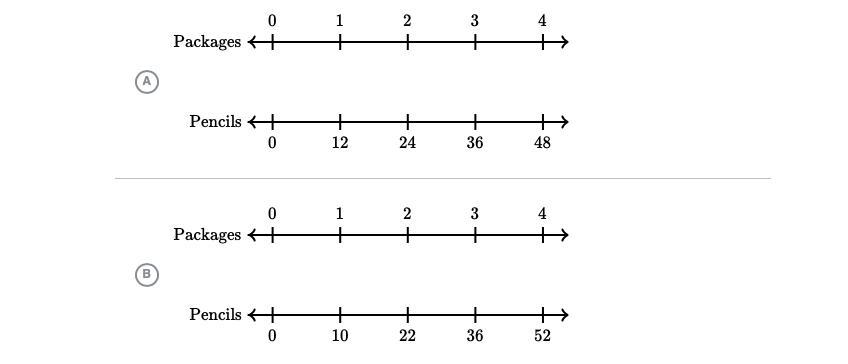
It's the first one. We notice that for every package there are 36/3 = 12 pencils. Therefore for 4 packages there will be 4*12 = 48 pencils.
Related Questions
(1 point) Let F (6z +6x^3) i + (2y +7z+ 7 sin(y^3)) j + (6x + 7y+2e^{z3}) k. (a) Find curl F.
Answers
the curl of the vector field F is given by:
curl\(F = (7 - 6z^2 e^{z3}) i - 6x^2 j + (6y^2 cos(y^3) + 1) k\)
The curl of a vector field F = F1 i + F2 j + F3 k is given by the following expression:
\(curl F = (∂F3/∂y - ∂F2/∂z) i + (∂F1/∂z - ∂F3/∂x) j + (∂F2/∂x - ∂F1/∂y) k\)
In this case, we have:
\(F = (6z + 6x^3) i + (2y + 7z + 7 sin(y^3)) j + (6x + 7y + 2e^{z3}) k\)
So, we need to compute the partial derivatives of each component of F with respect to x, y, and z:
\(∂F1/∂x = 18x^2\)
\(∂F1/∂y = 0\)
\(∂F1/∂z = 6\)
∂F2/∂x = 0
\(∂F2/∂y = 6y^2 cos(y^3) + 7\)
∂F2/∂z = 7
∂F3/∂x = 6
∂F3/∂y = 7
\(∂F3/∂z = 6z^2 e^{z3}\)
Now, we can use the formula for curl F to find:
\(curl F = (∂F3/∂y - ∂F2/∂z) i + (∂F1/∂z - ∂F3/∂x) j + (∂F2/∂x - ∂F1/∂y) k\)
\(= (7 - 6z^2 e^{z3}) i + (-6x^2) j + (6y^2 cos(y^3) + 7 - 6) k\)
\(= (7 - 6z^2 e^{z3}) i - 6x^2 j + (6y^2 cos(y^3) + 1) k\)
Therefore, the curl of the vector field F is given by:
\(curl F = (7 - 6z^2 e^{z3}) i - 6x^2 j + (6y^2 cos(y^3) + 1) k\)
To know more about vector field refer here:
https://brainly.com/question/24332269
#SPJ11
I need help with my math homework :(

Answers
We plug in 14 for x when we set the two equations equal to each other to prove they are equal.
So true LM congruent to MN

Solve the following systems of equations using Gaussian Elimination. 2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Find the inner product of two vectors A = (2, -3,0) and B = = (-1,0,5)
Answers
The inner product of two vectors A = (2, -3,0) and B = (-1,0,5) is -2 / √(13×26).
Solving the given system of equations using Gaussian elimination:
2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Matrix form of the system is
[A] = [B] 2 3 1 | 2 0 5 | 20 -1 2 3 | 13
Divide row 1 by 2 and replace row 1 by the new row 1: 1 3/2 1/2 | 1
Divide row 2 by 5 and replace row 2 by the new row 2: 0 1 1 | 4
Divide row 3 by -1 and replace row 3 by the new row 3: 0 0 1 | 5
Back substitution, replace z = 5 into second equation to solve for y, y + 5(5) = 20 y = -5
Back substitution, replace z = 5 and y = -5 into the first equation to solve for x, 2x + 3(-5) + 5 = 2 2x - 15 + 5 = 2 2x = 12 x = 6
The solution is (x,y,z) = (6,-5,5)
Therefore, the solution to the given system of equations using Gaussian elimination is (x,y,z) = (6,-5,5).
The given two vectors are A = (2, -3,0) and B = = (-1,0,5). The inner product of two vectors A and B is given by
A·B = |A||B|cosθ
Given,A = (2, -3,0) and B = (-1,0,5)
Magnitude of A is |A| = √(2²+(-3)²+0²) = √13
Magnitude of B is |B| = √((-1)²+0²+5²) = √26
Dot product of A and B is A·B = 2(-1) + (-3)(0) + 0(5) = -2
Cosine of the angle between A and B is
cosθ = A·B / (|A||B|)
cosθ = -2 / (√13×√26)
cosθ = -2 / √(13×26)
Learn more about equation at
https://brainly.com/question/12998758
#SPJ11
What statements are true?

Answers
Answer:
A. The number 81 is a rational number.
B. 11.7 is irrational
C. 3 is irrational
E. 17.35 is rational
Step-by-step explanation: A rational number is a number that can be expressed as a fraction where the numerator is a whole number (integer) and the denominator is a whole number (integer).
The number 81 is a rational number. We know this because it is possible to obtain the rational number 81 by dividing the integer 81 by the integer 1.
2/5 and 2/3 are rational numbers. Irrational numbers have an infinite number of digits to the right of the decimal point, without repetition.
The square root of 3 is irrational. It cannot be simplified further in its radical form and hence it is considered as a surd.
SOMEONE HELP PLEASE!

Answers
Answer:
x=48 and y is 132 my guy u welcome
Answer:
48 + y = 180
y= 132
5x - 17 = 132
x=29.8
If m∠2 = 120°, what is m∠7?

Answers
if angle m∠2 = 120°, then m∠7 is 120°.
What are Angles?An angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.
Supplementary angles are those angles that sum up to 180 degrees.
Given that m∠2 = 120°.
We have to find the m∠7.
m∠2 and m∠4 are supplementary angles.
120+m∠4=180
m∠4=60 degrees.
m∠4 is corresponding angle of m∠8.
m∠8 and m∠7 are again supplementary angles.
60+m∠7=180
m∠7=120 degrees.
Hence, if angle m∠2 = 120°, then m∠7 is 120°.
To learn more on Angles click:
brainly.com/question/28451077
#SPJ1
How do I find the measure of an angle?
Answers
Answer:
Step-by-step explanation:
The best way to measure an angle is to use a protractor. To do this, you'll start by lining up one ray along the 0-degree line on the protractor. Then, line up the vertex with the midpoint of the protractor. Follow the second ray to determine the angle's measurement to the nearest degree.
How do I find the measurement indicated in these problems.

Answers
Answer:
13. In parallelograms, adjacent angles are always supplementary. This means that angles that are right next to each other will always add up to 180.
So for this one, the two given angles add up to 180, creating this equation:
7x - 4 + 9x - 8 = 180
this can be simplified to x = 12
substitute x into <D to get <D = 100
since we know that <D and <A are supplementary, subtract m<D from 180 to get <A = 80
14. In parallelograms, opposite angles are always congruent, this means that in this problem <C and <A are equal to each other
so we can create an equation: 9x + 13 = 11x - 3
solve this to get x = 8
substitute 8 into <C's equation to get <C = 85
Since <C and <B are adjacent, subtract <C from 180 to get <B = 95
15. <J and <L are opposite to each other, so we know they are congruent
this means we can create an equation: 2 + 24x = 26x - 2
solve this to get x = 2
plug this into the equation for <J
you get <J = 50
16. In parallelograms, lines that are opposite to each other are always congruent. So this means that lines JM and KL are congruent
this means that we can create an equation of 2x - 15 = x - 4
solve this to get x = 11
plug in x to the equation for KL
you get KL = 7
Think of a matrix A and B which are both 3X3 matrices. Do not use all zeros or all
1’s!
3. Multiply A X B and record the result.
4. Multiply B X A and record the result
Answers
Answer:
9
Step-by-step explanation:
3x3 =9 hope this helps bbs
Enter the division problem 15 ÷11 as a fraction.
Answers
Answer: 15/11
Step-by-step explanation:
Answer:
15 ÷ 11 as a fraction is 15/11. As a mixed number it is 1 4/11.
Step-by-step explanation:
The scale on a map is 1 : 25000
How many kilometres on the ground is represented by 7 cm on the map?
Answers
Answer:
175000 km
Step-by-step explanation:
the 1:25000 essentially means that every centimeter represents 25000 kilometers. so the answer is 175000 by multiplying 7 and 25000
A skydiver's parachute opened at 3000 feet. Thirty seconds later, the skydiver's height was recorded at 2500 feet. What is the rate of change and what does it mean in this situation?
Answers
Suppose that 16 inches of wire cost 48 cents.
At the same rate, how much (in cents) will 42 inches of wire cost?
Answers
Answer:
the answer is 11.
if 16 inches of wire cost 48 cents your goal i to figure out how many inches of wire cots 33 cents to do so you have to find out how many cents each inch is. to do that you have to divide 48 by 16 and you get 3 so that mean that 1 inch costs 3 cents. after you figure that out you do 33 divided by 3 and you get 11. the answer is 11 inches costs 33 cents.
Step-by-step explanation:
so I am not that smart and need help please

Answers
Answer:
D
Step-by-step explanation:
please please please help meee

Answers
Answer:
-5 ≤ x ≤ 5
Step-by-step explanation:
If x^2 = 25
x = -5 or 5
BUT inequality
IF x is POSITIVE 5
You can square root both sides
x ≤ 5
IF x is NEGATIVE 5
You can divide both sides by -5
BUT switch inequality sign
This is because basically dividing both sides by negative
x ≥ -5
FINAL INEQUALITY
-5 ≤ x ≤ 5
c) √6 x √6 x√6 can someone help
Answers
Answer:
14.7
Step-by-step explanation:
Answer:
6\(\sqrt{6}\)
or
≈14.7
Step-by-step explanation:
√6 x √6 x√6 can someone help
√6 x √6 x√6 =
6\(\sqrt{6}\)
or
≈14.7
The following equation is true for all real values of n for which the expression on the left is defined, and B is a polynomial expression.

Answers
Answer:
6n^3
Step-by-step explanation:
3/3 *9^10/453*7+sqrt175
The polynomial expression is \($B=6 n^{3}\) ; where, \(\quad n \neq 0\).
What is Polynomial expression?Given:
\($\frac{n^{2}+12 n+27}{3 n^{3}+9 n^{2}} \div \frac{2 n^{2}+18 n}{B}=1$\)
To find:
the value of B is a polynomial expression.
Step 1
Let, \($\frac{n^{2}+12 n+27}{3 n^{3}+9 n^{2}} \div \frac{2 n^{2}+18 n}{B}=1$\)
\($\frac{\frac{n^{2}+12 n+27}{3 n^{3}+9 n^{2}}}{\frac{2 n^{2}+18 n}{B}}=1$$\)
Simplifying the above equation as
\($\frac{\frac{n^{2}+12 n+27}{3 n^{3}+9 n^{2}}}{\frac{2 n^{2}+18 n}{B}}: \frac{B}{6 n^{3}}$\)
then, we get
\($\frac{B}{6 n^{3}}=1$$\)
Step 2
Multiply both sides by \($6 n^{3}$\), then we get
\($\frac{B}{6 n^{3}} \cdot 6 n^{3}=1 \cdot 6 n^{3} $$\) where, \(\quad n \neq 0\)
Simplifying the equation as
\($B=6 n^{3}\) ; where, \(\quad n \neq 0\)
The value of \($B=6 n^{3}\) ; where, \(\quad n \neq 0\).
Therefore, the polynomial expression is \($B=6 n^{3}\) ; where, \(\quad n \neq 0\).
To learn more about polynomial expression
https://brainly.com/question/12978781
#SPJ2
find the cost in dollars of the operating a 200- ww lamp continuously for 1 week when the power utility rate is 13 cents/kwhcents/kwh .
Answers
In linear equation, Cost of operating a 200-W lamp continuously for 1 week = 6.7 $
What in mathematics is a linear equation?
A linear equation is a first-order (linear) term plus a constant in the algebraic form y=mx+b, where m is the slope and b is the y-intercept.The variables in the preceding equation are y and x, and it is occasionally referred to as a "linear equation of two variables."a first-degree algebraic equation with the variables y = 4x + 3 or some similar expression (that is, raised only to the first power). Such an equation has a straight line for its graph.1 kW = 1000 W
1 week = 7 days
1 day = 24 hours
Power utility rate = R = 20 cents/(kW.h)
Power consumed by the lamp = P = 200 W = 200 x 10-3 kW = 0.2 kW
Time period the lamp is operating for = T = 1 week = 1 x (7 x 24) hours = 168 hours
Energy consumed by the lamp in 1 week = E
E = PT
E = (0.2)(168)
E = 33.6 kW.h
Cost of operating the lamp continuously for 1 week = C
C = ER
C = (33.6)(20)
C = 672 cents
Converting from cents to dollars,
C = 672 x (1/100) $
C = 6.72 $
Rounding off to two significant figures,
C = 6.7 $
Cost of operating a 200-W lamp continuously for 1 week = 6.7 $
Learn more about linear equation
brainly.com/question/11897796
#SPJ4
16 is 20% of what number? Show your work and/or explain your reasoning.
Answers
Answer:
80
Step-by-step explanation:
To solve this problem you multiply 16 by 100 and then divide the total by 20 as follows:
(16 x 100) / 20
=80
Answer:
80
Step-by-step explanation:
Let's assume x as any no. multiply 20/100 equals 16 and then solve the equation in which you will get 80 as x.
The students in a class were asked wether they preferred football , tennis or hockey. The ratio of students who preferred football to tennis to hockeys is 14:8:3. What percentage of students preferred tennis
Answers
Answer:
32%
Step-by-step explanation:
Well, 14+8+3=25
So, 8/25=32/100, which means 32%
Answer:
Person above me is right
-2x + 3y = 9, solve for x
Answers
Answer:
If your going to graph it , it would be x=3/2y+ -9/2
Step-by-step explanation:
on a recent homework assignment, Eli needed to solve the equation d^2 = 49. He icorrectly wrote g = -7
Answers
Answer:
The solution set is {-7, 7}.
Step-by-step explanation:
He was half right .There are 2 solution d = -7 and d = 7.
How many 1/3 inch cubes does it take to fill a box with a width of 2 2/3inches, length 3 1/3 inches, and height of 2 1/3 inches?
Answers
Answer:
25
Step-by-step explanation
width= 8 cubes
length= 10 cubes
height= 7 cubes
A department store buys 100 shirts at a cost of $700 and sells them at a selling price of $10 each. Find the percent markup
Answers
Answer:
30%
Step-by-step explanation:
The price for each shirt to buy is: $ 700/100 = $ 7 / each
Selling price is: $ 10 / each
So the difference between the selling and buying prices is: $ 10 - $ 7 = $ 3
So 100 each, the interest is: $ 3 X100 = $ 300 => 30%
4 x 5-10 - 2 (1-2) + 5=
Answers
Answer:
\(17\)
Step-by-step explanation:
\(4\cdot \:5-10-2\left(1-2\right)+5\)
\(\mathrm{Follow\:the\:PEMDAS\:order\:of\:operations}\)
\(=4\cdot \:5-10-2\left(-1\right)+5\)
\(=20-10-2\left(-1\right)+5\)
\(=20-10-\left(-2\right)+5\)
\(20-10=10\)
\(=10-\left(-2\right)+5\)
\(-\left(-2\right)=+2\)
\(=10+2+5\)
\(10+2=12\)
\(=12+5\)
\(12+5=17\)
\(=17\)
Sally is seeking a loan with a simple interest rate of 8% per year. If she wants to
borrow $5,000, then how much will she be charged in interest for 2 years.
Answers
determine the unit normal vector to the curve with vector equation \vec r \, (t) =<1^t,\ln(4/t^2), \, \ln(e/(t^4)) > r (t)=<1 t ,ln(4/t 2 ),ln(e/(t 4 ))> at the point where t=2t=2.
Answers
the unit normal vector to the curve with vector equation \vec r \, (t) =<1^t,\ln(4/t^2), \, \ln(e/(t^4)) > r (t)=<1 t ,ln(4/t 2 ),ln(e/(t 4 ))> at the point where t=2t=2 is \vec n = <0,0,-1>
A unit normal vector is a normal vector with magnitude 1, and it points in the direction that is perpendicular to the tangent to the curve at a given point.
To determine the unit normal vector to a curve, it's important to find the tangent first and then find the normal. In this case, we're looking for the unit normal vector to the curve with the vector equation \vec r (t) =<1^t,\ln(4/t^2), \ln(e/(t^4)) > at the point where t = 2.
To find the unit normal vector to the curve with the vector equation \vec r (t) =<1^t,\ln(4/t^2), \ln(e/(t^4)) > at the point where t = 2, it is necessary to find the tangent to the curve and then find the normal. This is a crucial step in understanding the geometry of curves in 3D space.
To find the tangent to the curve, we'll differentiate the vector equation with respect to t and evaluate it at t = 2. The derivative of \vec r (t) is given by:
d\vec r/dt = <1, -2t^-3, -4e^-t^-4>
So the tangent to the curve at t = 2 is:
d\vec r/dt = <1, -2(2)^-3, -4e^-2^-4> = <1, 1.5, -1.648721>
Next, we'll find the normal to the tangent by taking the cross product of the tangent with a fixed vector, for example, the unit vector i = <1,0,0>. The cross product of two vectors results in a vector that is perpendicular to both of them.
The cross product of the tangent and the unit vector i is given by:
\vec T x \vec i = <1, 1.5, -1.648721> x <1,0,0> = <0,0,-1.5>
Since the magnitude of the normal is not 1, we'll normalize it by dividing it by its magnitude:
\vec n = \vec T x \vec i / ||\vec T x \vec i|| = <0,0,-1.5> / ||<0,0,-1.5>|| = <0,0,-1>
So the unit normal vector to the curve with the vector equation \vec r (t) =<1^t,\ln(4/t^2), \ln(e/(t^4)) > at the point where t = 2 is given by:
\vec n = <0,0,-1>
This is the unit normal vector that points in the direction that is perpendicular to the tangent to the curve at t = 2. The magnitude of 1 ensures that it's a unit vector and the direction points towards the normal direction.
To know mare about unit normal vector refer here:
https://brainly.com/question/29752499#
#SPJ11
Kala purchased a prepaid phone card for S15. Long distance calls cost 24 cents a minute using this card. Kala used her card only once to make a long
distance call. If the remaining credit on her card is $5.64, how many minutes did her call last?
Answers
\(15 - x = 5.64\)
\(15 - 5.64 = x\)
\(9.36 = x\)
//
\(9.36 \div 0.24 = 39\)
her call lasted 39 minutes.
Which criteria can be used to prove triangles are congruent select all that apply?
Answers
The four criteria that can be used to prove triangles are congruent and can be used to prove the triangles are congruent.
Triangle congruence: Two triangles are said to be congruent if all three of their corresponding sides and all three of their corresponding angles have the same measurements. These triangles can be moved around, rotated, flipped, and turned to have a same appearance. They match up with one another when moved.
The four criteria that can be used to prove triangles are congruent are SAS (Side-Angle-Side), ASA (Angle-Side-Angle), AAS (Angle-Angle-Side), and SSS (Side-Side-Side). Additionally, CPCTC (Corresponding Parts of Congruent Triangles are Congruent) can be used to prove the triangles are congruent.
Learn more about triangle here
https://brainly.com/question/2773823
#SPJ4
find the critical value tc for the confidence level c0.90 and sample size n=16.
Answers
The critical value, tc, for a confidence level of c0.90 and sample size n=16 can be found using a t-distribution table. The degrees of freedom for this calculation is n-1, which in this case is 15. From the table, we find that the tc value is approximately 1.753. This means that if we take a sample of size 16 from a population and calculate a sample mean, we can be 90% confident that the true population mean falls within a range of ± tc multiplied by the standard error of the sample mean. The critical value tc is an important factor in calculating confidence intervals for sample means.
To find the critical value, we need to use a t-distribution table, which provides the t-scores for various levels of confidence and degrees of freedom. The degrees of freedom for this calculation is n-1, which is 16-1=15. We look for the row in the table that corresponds to 15 degrees of freedom and then find the column that corresponds to a confidence level of 0.90. The value at the intersection of this row and column is the critical value, which in this case is approximately 1.753.
The critical value tc for a confidence level of c0.90 and sample size n=16 is approximately 1.753. This value is important in calculating confidence intervals for sample means, which allows us to estimate the range within which the true population mean is likely to fall with a certain level of confidence.
To know more about t-distribution visit:
https://brainly.com/question/13574945
#SPJ11