How do you find the midpoint of 30 < x ≤ 40
Answers
Answer:
To find the endpoint we have to calculate the distance between the known midpoint to the known endpoint. To calculate the midpoint we add two points and divide them by 2.
The formula for midpoint = (x1 + x2)/2, (y1 + y2)/2.
Substituting in the two x-coordinates and two y-coordinates from the endpoints.
Putting it together,
The endpoint formula is:
(x a ,ya)= ((2xm−xb),(2ym−yb))
( x a , y a ) = ( ( 2 x m − x b ) , ( 2 y m − y b ) ).
The end of a line at a point that is equally distant from both ends, a time interval between an event's beginning and end.
The point on a graph or figure where the figure stops might be referred to as the endpoint. It can be the point joining the sides of a polygon (the vertex), the common endpoint of two rays making an angle, the two extreme points of a line segment, the one end of a ray.
To learn more about endpoints and midpoints:
Step-by-step explanation:
this is just an exaple
Related Questions
6+2 (x+4) = 1/2 (3-x)

Answers
Answer:
x² - 8x + 12
Step-by-step explanation:
(x - 2) (x - 6)
x² -6x -2x + 12
x² - 8x + 12
The picture shows the equation like that, so I solve it that way!
Answer:
\(\tt x ^2-8x+12\)Step-by-step explanation:
\(\tt (x-2)(x-6)\)
Use the FOIL method:-
→ \(\boxed{\bf (a+b)(c+d)=ac+ad+bc+bd}\)
\(\tt x^2-6x-2x+12\)
Combine like terms:-
\(\tt x^2+(-6x-2x)+12\)
Simplify:-
\(\tt x ^2-8x+12\)
______________________
Hope this helps! :)
write down the update formula for 12(x1, x2) up to a proportionality constant. this time, you can write it in terms of expected values, but do not include unnecessary terms.
Answers
update formulas are up to a proportionality constant, which can be ignored in practice.
Assuming that 12(x1, x2) refers to a data set of 12 observations of two variables x1 and x2, the update formula for the mean vector of the data set can be written in terms of expected values as:
E[x] = (1/n) * Σ(E[x_i])
where E[x_i] is the expected value of the ith observation of the vector x, and n is the total number of observations.
The update formula for the covariance matrix of the data set can be written as:
E[Σ] = (1/n) * Σ(E[(x_i - E[x])(x_i - E[x])^T])
where E[(x_i - E[x])(x_i - E[x])^T] is the expected value of the outer product of the deviation of the ith observation from the mean vector. The ^T symbol denotes the transpose of a vector.
Note that these update formulas are up to a proportionality constant, which can be ignored in practice.
learn about update formula,
https://brainly.com/question/30648198
#SPJ11
3/7x - 2/14 = 3 solve using algebraic method
Answers
Step-by-step explanation:
3/7x - 2/14 = 3
6x-2/14=3
6x-2=42
6x=44
x=22/3
the full screen guys

Answers
Answer:
(-2 2/3,0)
(0,2)
Step-by-step explanation:
Just did it
Answer:
Step-by-step explanation:
the two points are(0,2), (-8/3,0)

find the slope of the line that passes through points (2,8) and (1,3)
Answers
Answer:
Slope is m = 5
Step-by-step explanation:
Melanie has $64 in her checking account. She writes a check for $75. What is Melanie's checking account balance after writing the check?
Answers
Answer:
if adding its 139 if u subtract then its 11
Step-by-step explanation:
The average height of women in the United states Is 65.5 Inches with a standard deviation of 2.5. Find the probability that a woman randomly selected will be 60 inches or less.
Answers
The probability that a randomly selected woman will be 60 inches or less is approximately 0.0139, or 1.39%.
To find the probability that a randomly selected woman will be 60 inches or less, we need to calculate the area under the normal distribution curve up to 60 inches.
First, we need to standardize the height using the z-score formula:
z = (x - μ) / σ
where:
x = 60 inches (the value we want to find the probability for)
μ = mean height = 65.5 inches
σ = standard deviation = 2.5 inches
Substituting the values into the formula, we get:
z = (60 - 65.5) / 2.5
z = -2.2
Next, we need to find the cumulative probability up to the z-score of -2.2. We can look up this value in the standard normal distribution table or use statistical software.
Using a standard normal distribution table, we find that the cumulative probability corresponding to a z-score of -2.2 is approximately 0.0139.
Therefore, the probability that a randomly selected woman will be 60 inches or less is approximately 0.0139, or 1.39%.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
Someone please help by tonight I’m struggling very hard

Answers
Drawing a 10 from the bag unlikely
Rolling a number less than 5 Likely
Drawing a red marble equally likely and unlikely
Here is the completed frequency table:
Number frequency
1 9
2 12
3 10
4 8
5 5
6 6
Hiro's prediction is likely.
What is the probability?
Probability determines the odds that a random event would happen. If the probability value is 0.5, it is equally likely and unlikely that the event would happen. If it is less than 0.5, it is unlikely that the event would happen. If it is greater than 0.5, it is likely that the event would happen.
Probability of drawing a 10 = number of 10s in the bag / total number in the bag = 1/100 = 0.01
It is unlikely that you would draw a 10.
Probability of rolling a number less than 5 = numbers that are less than 5 / total number of sides = 4/6 = 0.67
It is likely that a number less than 5 would be rolled.
Probability of drawing a red marble = total number of red marbles / total number of marbles = 8 / 16 = 0.5
It is equally likely and unlikely that a red marble would be picked
In order to determine the frequency, if the denominator of the relative frequency of the number is equal to 50, then the numerator is equal to the frequency. In the case where the denominator is less than 50, divide 50 by the number, multiply the quotient by the numerator in order to determine the frequency.
The frequency of 2 = (50 / 25) x 6 = 12
Number frequency
1 9
2 (6 x 2) 12
3 (1 x 10) 10
4 (4 x 2) = 8
5 (1 x 5) 5
6 (3 x 2) 6
To learn more about probability, please check: https://brainly.com/question/13234031
#SPJ1
i need help with this question please a and b


Answers
The probability that a college student has between $31500 and $47550 is 0.2715
Explanation:Given:
The average student loan = $25200
The standard deviation = $13500
The distribution is normal
To find:
a) the distribution of X
b) the probability that the college graduate has between $31500 and $47550 in student loan
a) X = the student loan debt of randomly selected college graduat
To write the value of X and N in the formwritten:
The 1st parenthesis = average student loan = $25200
The 2nd parenthesis = standard deviation = $13500
\(X-N\text{ \lparen25200, 13500\rparen}\)b) To get the probability that college student has between $31500 and $47550, we will apply the z-score formula:
\(\begin{gathered} \begin{equation*} z=\frac{X-μ}{σ} \end{equation*} \\ X=\text{ value/score} \\ \mu\text{ = mean} \\ \sigma\text{ = standard deviation} \end{gathered}\)\(\begin{gathered} when\text{ X = 31500} \\ z\text{ = }\frac{31500\text{ - 25200}}{13500} \\ z\text{ = 0.4667} \\ Using\text{ a standard normal table/calculator, the probability for z = 0.4667 is 0 67963} \end{gathered}\)\(\begin{gathered} when\text{ X = 47550} \\ z\text{ = }\frac{47550\text{ - 25200}}{13500} \\ z\text{ = 1.6556} \\ Using\text{ a standard normal table/calculator, the probability for z = 1.6556 is 0.95109} \end{gathered}\)The probability that a college student has between $31500 and $47550 will be the difference in probability
\(\begin{gathered} =\text{ 0.95109 - 0.67963 = 0.27146} \\ The\text{ probability }=\text{ 0.2715} \\ \end{gathered}\)What is the Lowest common multiple of eight and six
Answers
Answer:
24
Step-by-step explanation:
8= 8, 16 ,24 , 32 , 40, 48, 56, 64, 72, 80
6= 6, 12, 18, 24, 30, 36, 42, 48, 54, 50
Answer:
Step-by-step explanation:
Yo come let's talk
then
A dress is on sale for d dollars. The regular price is 3 times as much.
Janine has enough money to buy 2 dresses at the regular price.
How many dresses can Janine buy at the sale price?
A.
1 dress
B.
3 dresses
C.
6 dresses
D.
9 dresses
Answers
Answer:
6
Step-by-step explanation:
hope this helps, have a good day
A player kicks a football off the ground so that if travels with a velocity of 32 miles per hour at an angle of 34° with the ground. Find the magnitude of the horizontal and vertical components.
Answers
As a result, the horizontal component of velocity has a magnitude of 11.8 m/s\ while the vertical component of velocity has a value of 8.0 m/s.
What is velocity?The pace at which an item changes its position is described by a vector quantity called velocity. It is described as the rate at which displacement changes in relation to time The amount and direction of velocity are both present. Speed refers to the velocity's magnitude.
The football's velocity in this scenario is 32 miles per hour, or around 14.3 meters per second.
We can use trigonometry to determine the sizes of a velocity vector's horizontal and vertical components.
Vₓ = V cos (theta), where V is the magnitude of the velocity vector and theta is the angle that the velocity vector makes with the horizontal axis, gives the horizontal component of velocity.
Vy = V sin (theta), where V is the magnitude of the velocity vector and theta is the angle that the velocity vector makes with the horizontal axis, gives the vertical component of velocity.
In this instance, we are aware of the football's velocity, which is 32 miles per hour, or around 14.3 meters per second6. It makes a 34 degree 6 angle with the ground.
Therefore,
Vₓ= V cos (theta) * cos (34 degrees) = 14.3 m/s * 11.8 m/s
Vy = V sin (theta) * sin (34 degrees) = 14.3 m/s * 8.0 m/s
To know more about velocity visit:
brainly.com/question/30559316
#SPJ1
Find the radius of convergence,R, of the series.
Find
the radius of convergence,R,
of the series.
9(?1)nnxn
Find
the radius of convergence,R,
of the series.
n= 1
R=
Find the interval,I, of convergence of the series. (Enter answer using interval notation.)
I=
Answers
The radius of convergence,R, of the series \(\[ \sum_{n=1}^{\infty} ~9(-1)^n~ nx^n \]\) is (1, ∞)
We know that for a power series ∑an (x - p)^n
if |x - p| < R then the series converges,
and if |x - p| > R then the series diverges.
Here, the number R is called the radius of convergence.
We have been given a series \(\[ \sum_{n=1}^{\infty} ~9(-1)^n~ nx^n \]\)
We need find the radius of convergence.
We use ratio test.
We know for \($\lim_{x\to\infty}~ | \frac{a_{n+1}}{a_n}|=L\)
if L < 1, then the series converges
and If \($\lim_{x\to\infty}~a_n \neq 0\) then \(\sum a_n\) diverges.
Using ratio test for given series,
\($\lim_{x\to\infty}~ | \frac{9(-1)^{n+1}~ (n+1)x^{n+1}}{9(-1)^n~ nx^n}|\\\\\\\)
= \($\lim_{x\to\infty}~ | \frac{(n+1)x^{n+1}}{nx^n}|\)
= \($\lim_{x\to\infty}~ | \frac{(n+1)x}{n}|\)
\(=|x| $\lim_{x\to\infty}~ | \frac{n+1}{n}|\)
= |x|
This means, the series is convergent for |x| < 1.
Learn more about the radius of convergence here:
https://brainly.com/question/18763238
#SPJ4
Annabelle has 6 posters she wants to hang on the wall. How many different ways can the posters be arranged in a row?
Answers
Answer: 720
Step-by-step explanation: 6 x 5 x 4 x 3 x 2 x 1 = 720
Which statement is true regarding the traits of scatter plots
Answers
Answer: A
Step-by-step explanation:
JUST TOOK THE QUIZ
3. An isosceles right triangle is a right triangle with congruent legs. If the length of each leg is represented by x, what algebraic expression can be used to represent the length of the hypotenuse? Explain your reasoning
please don't answer if you don't know
Answers
Answer:
Step-by-step explanation:
right triangle means Pythagorean theorem!
a^2+b^2=c^2
if each leg (a and b) = x, then
x^2+x^2=c^2
2x^2=c^2
solving for c by taking the square root of both sides leaves
c=x×sqrt(2)
c must be positive since its a length, so no need for a +- I. this case
A radar tends to overestimate the distance of an aircraft, and the error is a normal random variable with a mean of 50 meters and a standard deviation 100 meters. What is the probability that the measured distance will be smaller than the true distance?.
Answers
Check answer below in the image.

Frank started an assignment at 6:26 PM and finished it at 7:44 PM. How long did it take him? Give your answer in minutes.
Answers
1.18 in minutes is 78 minutes bc 1 hour is 60 minutes + 18 minutes is 78
Hope this helps :D
Answer:
78 minutes
Step-by-step explanation:
7:44 PM
6:26 PM
--------------
1:18
1 hour and 18 minutes
1 hour is 60 minutes
so 60 minutes + 18 minutes = 78 minutes
In the diagram below AB = BC and BCD = 110 find A with justification
Answers
Result:
A (is an angle) = 70°.
How to calculate angle A?Based on the provided information:
AB = BC
BCD = 110
We can use the information to find the value of A.
Since AB = BC, we can assume that triangle ABC is an isosceles triangle, where AB and BC are the two equal sides. For an isosceles triangle, the angles opposite to the equal sides are also equal.
So, ∠ABC = ∠BCA (opposite angles of an isosceles triangle are equal).
Since BCD = 110, we can deduce that ∠BCA + ∠ BCD = 180 (sum of angles in a triangle equals 180 degrees).
Substituting the values, we get:
∠BCA + 110 = 180
Subtracting 110 from both sides, we get:
∠BCA = 180 - 110
∠BCA = 70
Now, since ∠ABC = ∠BCA, we have:
∠ABC = 70°
Therefore, A = 70 degrees.
Read more about isosceles triangle at brainly.com/question/29618252
#SPJ1
What is the mode for this set of data? 5,6,13,2,6,11,6,5,3,14
Answers
Answer:
6
Step-by-step explanation:
6 appears the most
Answer:
6
Step-by-step explanation:
Put the data in order from smallest to largest
5,6,13,2,6,11,6,5,3,14
2,3,5,5,6,6,6,11,13,14
The mode is the number that appears most often
6 appears most often so it is the mode
You flipped a fair coin 10 times. The result were 7 heads and 3 tails. Is the next flip more likely to be heads, tails, or the same likelihood of heads or tails? Explain your answer using complete sentences.
Answers
Two polynomials P and D are given. Use either synthetic or long division to divide P(x) by D(x), and express P in the form P(x) = D(x) Q(x) + R(x).
P(x) = 3x³-4x²-3x, D(x) = 3x - 4
P(x) =
Answers
The value of Q(x) = x² - 1
R(x) = 4
What is Long Division?
Long division is a common division procedure in mathematics that may be easily performed manually and is appropriate for dividing multi-digit Hindu-Arabic numbers. It simplifies a division problem into several shorter stages.
By long Division method:
x² - 1
_______________________________
(3x - 4) | 3x³ - 4x² - 3x
3x³ - 4x²
_________________
0 - 0 - 3x
- 3x + 4
___________________
0 + 4
Q(x) = x² - 1
R(x) = 4
Hence, (3x³-4x²-3x) = (3x - 4)(x² - 1 ) + 4
To learn more about Long Division method click on the link
https://brainly.com/question/25289437
#SPJ13
A kitchen floor is in the shape of a square.
The area of the floor is 529 ft. What is the
length of a side of the kitchen floor?
Answers
Answer:
132.25
Step-by-step explanation:
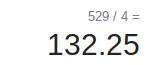
PLSSSS HELP IF YOU TURLY KNOW THISSS

Answers
1. Multiply both sides by 2. 4 + 3x = 5 * 2
2. Simplify. 4 + 3x = 10
3. Subtract 4 from both sides to single out x. 3x = 10 - 4
4. Simplify. 3x = 6
5. Divide by 3. x = 6/3
6. Simplify. x = 2
Input 2 into the original equation to check this answer and you will get 5 = 5 which means that x = 2 is your final answer.
Answer: x = 2
Step-by-step explanation:
To solve for x, we will isolate the variable (x).
Given:
\(\displaystyle \frac{4+3x}{2}=5\)
Multiply both sides of the equation by 2:
4 + 3x = 10
Subtract 4 from both sides of the equation:
3x = 6
Divide both sides of the equation by 3:
x = 2
In your reservoir, you have a production well which flows for 48 hours at 200 STB/day, and then shut-in for 24 hours. The following additional data are given : Pi = 3100 psi Ct = 15x10^-6 psi^-1 Bo = 1.3 bbl/STB ϕ = 15% μ=1.2 cp K = 45 md and h = 60 ft
a-) Calculate the pressure in this production well at 12 hours of shut in
b-) Explain how can you use superposition in time to analyze a pressure build-up test.
Answers
a) To calculate the pressure at 12 hours of shut-in:
substitute the given values into the pressure buildup equation and solve for P(t=12).
b) Superposition in time is used in pressure buildup analysis by adding or summing the responses of multiple transient tests to analyze and interpret reservoir behavior and properties.
We have,
a) To calculate the pressure in the production well at 12 hours of a shut-in, we can use the equation for pressure transient analysis during shut-in periods, known as the pressure buildup equation:
P(t) = Pi + (Q / (4πKh)) * log((0.14ϕμCt(t + Δt)) / (Bo(ΔP + Δt)))
Where:
P(t) = Pressure at time t
Pi = Initial reservoir pressure
Q = Flow rate
K = Permeability
h = Reservoir thickness
ϕ = Porosity
μ = Viscosity
Ct = Total compressibility
t = Shut-in time (12 hours)
Δt = Time since the start of the flow period
Bo = Oil formation volume factor
ΔP = Pressure drop during the flow period
Given:
Pi = 3100 psi
Q = 200 STB/day
K = 45 md
h = 60 ft
ϕ = 15%
μ = 1.2 cp
Ct = 15x10^-6 psi^-1
Bo = 1.3 bbl/STB
t = 12 hours
Δt = 48 hours
ΔP = Pi - P(t=Δt) = Pi - (Q / (4πKh)) * log((0.14ϕμCt(Δt + Δt)) / (Bo(ΔP + Δt)))
Substituting the given values into the equation:
ΔP = 3100 - (200 / (4π * 45 * 60)) * log((0.14 * 0.15 * 1.2 * 15x\(10^{-6}\) * (48 + 48)) / (1.3 * (3100 - (200 / (4π * 45 * 60)) * log((0.14 * 0.15 * 1.2 * 15 x \(10^{-6}\) * (48 + 48)) / (1.3 * (0 + 48))))))
After evaluating the equation, we can find the pressure in the production well at 12 hours of shut-in.
b) Superposition in time is a principle used in pressure transient analysis to analyze and interpret pressure build-up tests.
It involves adding or superimposing the responses of multiple transient tests to simulate the pressure behavior of a reservoir.
The principle of superposition states that the response of a reservoir to a series of pressure changes is the sum of the individual responses to each change.
Superposition allows us to combine the information obtained from multiple tests and obtain a more comprehensive understanding of the reservoir's behavior and properties.
It is a powerful technique used in reservoir engineering to optimize production strategies and make informed decisions regarding reservoir management.
Thus,
a) To calculate the pressure at 12 hours of shut-in:
substitute the given values into the pressure buildup equation and solve for P(t=12).
b) Superposition in time is used in pressure buildup analysis by adding or summing the responses of multiple transient tests to analyze and interpret reservoir behavior and properties.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ12
pproximately what percentage of the observations fall between 95.5 and 109.5? b. approximately what percentage of the observations are greater than 88.5? c. approximately what percentage of the observations fall between 109.5 and 116.5?
Answers
Approximately 68% of the observations fall between 18 and 22, and 95% of the observations fall between 16 and 24.
Data drawn from a bell-shaped distribution with a mean of 20 and a standard deviation of 2 can be used to calculate the percentage of observations that fall between 18 and 22, and 16 and 24. To calculate this percentage, we first need to find the z-score for each of the lower and upper boundaries.
The z-score for 18 is -1 and the z-score for 22 is 1. We can use a standard normal table to look up the area under the curve between -1 and 1, which is 0.68. Thus, 68% of the observations fall between 18 and 22. To calculate the percentage of observations between 16 and 24, we need to find the z-score for 16 and 24, which are -2 and 2 respectively.
We can look up the area under the curve between -2 and 2 in a standard normal table, which is 0.95. Thus, 95% of the observations fall between 16 and 24. To calculate the percentage of observations less than 16, we need to find the z-score of 16, which is -2. We can look up the area under the curve.
For more questions like Bell-shaped click the link below:
https://brainly.com/question/26686815
#SPJ4

please help me out thanks

Answers
Answer:
I think it would be either $134.89 or 113.22
Step-by-step explanation:
just from an estimate, I got close to one of these two
The length and width of a rectangle are 1.125 m and 0.606 m, respectively. Multiplying, your calculator gives the product as 0.68175. Rounding properly to the correct number of significant figures, the area of the rectangle should be written as
Answers
The area of the rectangle should be written as 0.682 m². To determine the area of a rectangle, you multiply its length by its width. The length of the rectangle is 1.125 m, and the width is 0.606 m.
Area of rectangle = length x widthA = 1.125 m x 0.606 mA = 0.68175 m²Now, rounding the answer to the correct number of significant figures, which is 3. The digit after the third significant figure is 7 which is greater than 5, therefore the third digit should be rounded up. So the final answer will be 0.682 m².
Thus, the long answer to this question is: After multiplying the length and width of a rectangle of dimensions 1.125 m and 0.606 m respectively, the product obtained from the calculator is 0.68175. To find the area of the rectangle, we use the formula A = l × w, which gives A = 1.125 m × 0.606 m = 0.68175 m². Rounding this answer to 3 significant figures, we find that the third digit is 1 which is greater than 5. Therefore, we must round the third digit up to get the final answer of 0.682 m².
To know more about rectangle visit:
https://brainly.com/question/10834438
#SPJ11
can someone help me please!!!!!!!!!

Answers
Answer:
y=2x-5
Step-by-step explanation:
The slope is 2(run 2, row 1 so 2/1=2) and the y intercept is -5(where the line crosses over the y axis)
Equation- y=2x-5
Ask me if you need further explanation!
Enlarge shape A by scale factor
1
3
with centre of enlargement (-3, -6).
What are the coordinates of the vertices of the image?

Answers
Check the picture below.
