How do we find the slope of a line that is given in slope-intercept form?
Choose 1 answer:
The slope is the first number that appears in the equation.
The slope is the coefficient of x, regardless of order.
Answers
Answer:
The slope is the coefficient of x, regardless the order.
Step-by-step explanation:
Related Questions
a rancher has 10,000 linear feet of fencing and wants to enclose a rectangular field and then divide it into two equal pastures, with an internal fence parallel to one of the rectangular sides. what is the maximum area of each pasture? round to the nearest square foot.
Answers
For a 10,000 linear feet of fencing and wants to enclose a rectangular field, the maximum area of each pasture is equals to the 2,083,333.33 square feet .
A rancher wants to enclose about 10,000 linear feet of fencing in a rectangular field. There are two equal pastures. Let, W the Width and L the Length with 3 pieces. The total length will be equal to 2W + 3L. As we know, the Area of rectangle, A = L×W ---(1)
Perimeter of rectangle = 10,000 feet, so sum of all sides of rectangle, 2W + 3L = 10000
Solve for determining value of L, 3L
= 10000 - 2W
\(L = \frac{ 10000 - 2W }{3}\)
Substitutes for L into the first equation, A = L×W
\(A = W(\frac{ 10000 - 2W }{3})\)
For maximum area, set the 1st derivative = 0.
differentiating above Area equation w.r.t W,\( A = \frac{(10000 \: W - 2W^2)}{3}\)
\( \frac{dA}{dW} = \frac{d(\frac{10000 \: W - 2W^2}{3})}{dW}\)
=> \(\frac { 1}{3}(10000 - 4W) = 0 \)
=> W = 2500 meters
Now, using above relation, 2W + 3L= 10000
=> 5000 + 3L = 10000
=> 3L = 5000
=> L = 1667 meters
Area = 2500× 5000/3 = 4,166,666.67 sq feet. Now, maximum area of each pasture
= 4,166,666.67/2 = 2,083,333.33333 sq. feet. Hence, required value is 2,083,333.33 sq. feet.
For more information about area of rectangle, refer:
https://brainly.com/question/26290174
#SPJ4
The area of sector AOB is 210.25 cm². What is the exact area of the shaded region?
До
0 29 cm
B
OA. (210.25 -420.5) cm²
OB. (210.25-841) cm²
OC. (210.25 -420.5√√2) cm²
OD. (210.25-841 √2) cm²

Answers
The area of the segment is 210.25π - 420.5
What is area of segment?A segment is an interior region of a circle. It is the space between a chord and an arc.
The area of segment is expressed as;
area of segment = area of sector - area of triangle
The shaded part is a segment.
A sector is a region between two radii and an arc.
Area of triangle = 1/2 × 29 × 29
= 841/2
= 420.5
The area of the sector is given as 210.25
Therefore the area of the segment = 210.25π - 420.5
learn more about area of segment from
https://brainly.com/question/22599425
#SPJ1
plz help!! math isn’t my thing!! i’ll give brainliest!!

Answers
Answer:
3x + 5 + 6x -6 = 80
9x -1 = 80
9x = 81
x = 9
3(9) +5 = 32
< DBC = 32
6(9)-6 = 48
<ABC = 48
Plot the point (−1/2, −5/2) on the coordinate plane.

Answers
Note: -1/2=-0.5 and -5/2=-2.5

Which of the following statements is NOT true regarding an expression written in scientific notation in the form of a times 10 Superscript n baseline?
A. The value of a must be greater than or equal to 1 and smaller than 10.
B. The value of n must be an integer.
C. Doubling n results in a doubling of the value of the expression.
D. Doubling a results in a doubling of the value of the expression.
Answers
Have a great day :)
Find the measure of the angle indicated below. 162 130 ?
Answers
Answer:
162 is greater than 130.. if that's what your are talking about..
I was a little confused on this problem

Answers
Answer:
Step-by-step explanation:
164.8+106.09=270.89
gong rented a truck for one day. There was a base fee of $19.95, and there was an additional charge of 71 cents for each mile driven. Hong had to pay $125.74 when he returned the truck. For how many miles did he drive the truck?
Answers
Answer:
19.95 + .71 × x = 125.74
x = 141.053
x is the answer
Evaluate (a + b)2 for a = 2 and b=3.
A. 13
B. 10
C. 25
(the two is an exponent)
Answers
Answer:
C. 25
Step-by-step explanation:
(a + b)²
= (2 + 3)²
= (5)²
= 25
hope this helps...
D.1 Give an estimate for the total volume of food and water you've ingested in the last day, in milliliters. D.2 How many times larger is the amount of blood your heart has pumped in the last day than the amount of food and drink you took in? D.3 How much error do you expect in your answer to 4 b ? You should give an quantitative response to this, but not one generated by a formula. Instead, estimate the error by examining how closely you think you know the values you estimated for food intake and blood flow. You don't need to use advanced error propagation; an approximate response is fine. D.4 What is the relevance of this calculation to the theory that all the blood that flows through your veins is generated in the liver?
Answers
An estimate for the total volume of food and water you've ingested in the last day is 3000-5000 milliliters. On average, the heart pumps about 5 liters of blood per minute. 10-20% or more error I'm expecting. Calculating heart blood volume compared to food and drink consumption is crucial for understanding circulation and liver function.
D.1 Estimating the amount of food and water consumed in a day can be difficult without specific measurements, but a rough estimate can be made based on typical intake amounts. On average, a person may consume 2-3 liters of water and 1000-2000 calories per day, resulting in an estimated total volume of 3000-5000 milliliters.
D.2 The amount of blood pumped by the heart varies from person to person and depends on factors such as heart rate and overall health. On average, the heart pumps about 5 liters of blood per minute, which is much larger than the estimated volume of food and water intake.
D.3 Estimating food and water intake and blood flow is prone to error due to variability and uncertainties in personal measurements. Individuals' habits, health, and physical activity levels can affect these estimates, potentially resulting in a significant error of 10-20% or more.
D.4 The calculation of the heart's blood volume compared to food and drink consumption is crucial for understanding the circulation system and liver role.
The liver processes nutrients, detoxifies, and produces blood components, while the heart is responsible for circulating blood throughout the body. The vast difference in volume between the two is emphasized, emphasizing the heart's crucial role in maintaining circulation.
To know more about blood refer here:
https://brainly.com/question/30828552#
#SPJ11
If 3x - 5 = 22, find the value of 2x.
a. 6
b. 24
c. 12
d. 18
Answers
Answer:
d. 18
Step-by-step explanation:
3x - 5 = 22
3x = 27
x = 9
Then, 2x is equal to:
= 2(9)
= 18
please help
evaluate the expression 3^3.(12-12)divide by 2
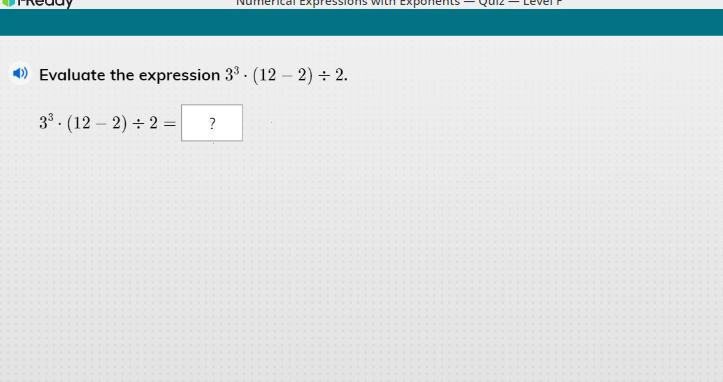
Answers
Answer:
The answer is 135. Brainliest?
Step-by-step explanation:
Answer:
135
Step-by-step explanation:
Using an example, outline the steps involved in performing a
Wald test to test significance of a sub-group of coefficients in a
multiple regression model.
Answers
The Wald test is a statistical test that can be used to test the significance of a group of coefficients in a multiple regression model.
The test statistic is calculated as the ratio of the estimated coefficient to its standard error. If the test statistic is significant, then the null hypothesis that the coefficient is equal to zero can be rejected.
Suppose we have a multiple regression model with three independent variables: age, gender, and education. We want to test the hypothesis that the coefficients for age and education are both equal to zero. The Wald test statistic would be calculated as follows:
Test statistic = (Estimated coefficient for age) / (Standard error of estimated coefficient for age) + (Estimated coefficient for education) / (Standard error of estimated coefficient for education)
If the test statistic is significant, then we can reject the null hypothesis that the coefficients for age and education are both equal to zero. This would mean that there is evidence that age and education are both associated with the dependent variable.
The Wald test is a powerful tool that can be used to test the significance of a group of coefficients in a multiple regression model. However, it is important to note that the test statistic is only valid if the assumptions of the multiple regression model are met. If the assumptions are not met, then the p-value of the Wald test may be inaccurate.
Here are some of the assumptions of the multiple regression model:
* The independent variables are independent of each other.
* The dependent variable is normally distributed.
* The errors are normally distributed.
* The errors have constant variance.
If any of these assumptions are not met, then the Wald test may not be accurate.
Learn more about multiple regression model here:
brainly.com/question/32816836
#SPJ11
Which expression represents the volume of the prism in terms of w, the width of the base? 5w2 cubic units 6w2 cubic units 5w3 cubic units 6w3 cubic units
Answers
The expression that represents the volume of the rectangular prism, in terms of the width w, is given as follows:
6w³ cubic units.
How to obtain the volume of a rectangular prism?A rectangular prism is composed by three dimensions, given as follows:
Length l.Width w.Height h.The volume of the rectangular prism is given by the multiplication of these three dimensions, as follows:
V = lwh.
From the image given at the end of the answer, the dimensions of the prism are given as follows:
Width w.Length l = 2w.Height h = 3w.Hence the expression that gives the volume of the rectangular prism is given as follows:
V = w x 2w x 3w = 6w³ cubic units.
Missing InformationThe prism is given by the image shown at the end of the answer.
More can be learned about the volume of a rectangular prism at https://brainly.com/question/22070273
#SPJ1

10. Prove that if f is uniformly continuous on I CR then f is continuous on I. Is the converse always true?
Answers
F is continuous at every point x₀ ∈ I. Thus, f is continuous on an interval I.
Regarding the converse, the statement "if f is continuous on an interval I, then it is uniformly continuous on I" is not always true. There exist functions that are continuous on a closed interval but not uniformly continuous on that interval. A classic example is the function f(x) = x² on the interval [0, ∞). This function is continuous on the interval but not uniformly continuous.
To prove that if a function f is uniformly continuous on interval I, then it is continuous on I, we need to show that for any ε > 0, there exists a δ > 0 such that for any x, y ∈ I, if |x - y| < δ, then |f(x) - f(y)| < ε.
Since f is uniformly continuous on I, for the given ε, there exists a δ > 0 such that for any x, y ∈ I, if |x - y| < δ, then |f(x) - f(y)| < ε.
Now, let's consider an arbitrary point x₀ ∈ I and let ε > 0 be given. Since f is uniformly continuous, there exists a δ > 0 such that for any x, y ∈ I, if |x - y| < δ, then |f(x) - f(y)| < ε.
Now, choose δ' = δ/2. For any y ∈ I such that |x₀ - y| < δ', we have |f(x₀) - f(y)| < ε.
Therefore, for any x₀ ∈ I and ε > 0, we can find a δ' > 0 such that for any y ∈ I, if |x₀ - y| < δ', then |f(x₀) - f(y)| < ε.
This shows that f is continuous at every point x₀ ∈ I. Thus, f is continuous on interval I.
Learn more about arbitrary point:
https://brainly.com/question/19195471
#SPJ11
please help me!! i need it asap

Answers
A random sample of n = 16 scores is obtained from a normal population with m = 40 and s = 8. what is the probability that the sample mean will be within 2 points of the population mean?
Answers
Using the normal distribution, there is a 0.6826 = 68.26% probability that the sample mean will be within 2 points of the population mean.
Normal Probability DistributionThe z-score of a measure X of a normally distributed variable with mean \(\mu\) and standard deviation \(\sigma\) is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score measures how many standard deviations the measure is above or below the mean. Looking at the z-score table, the p-value associated with this z-score is found, which is the percentile of X.By the Central Limit Theorem, the sampling distribution of sample means of size n has standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).For this problem, the parameters are given as follows:
\(\mu = 40, \sigma = 8, n = 16, s = \frac{8}{\sqrt{16}} = 2\)
The probability that the sample mean will be within 2 points of the population mean is the p-value of Z when X = 40 + 2 = 42 subtracted by the p-value of Z when X = 40 - 2 = 38, hence:
X = 42:
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
Z = (42 - 40)/2
Z = 1
Z = 1 has a p-value of 0.8413.
X = 38:
\(Z = \frac{X - \mu}{s}\)
Z = (38 - 40)/2
Z = -1
Z = -1 has a p-value of 0.1587.
0.8413 - 0.1587 = 0.6826 = 68.26% probability that the sample mean will be within 2 points of the population mean.
More can be learned about the normal distribution at https://brainly.com/question/24537145
#SPJ1
To join a local square dancing group, Jan has to pay a $100 sign-up fee plus $25 per month. Write an equation for the cost (y) based on the number of months.
a. y = 25x + 100
b. y = 100x + 25
c. y = 25 + 100x
d. y = 100 + 25x
Answers
The correct answer is option A which is y = 25x + 100.
Given the following:
To join a local square dancing group, Jan has to pay a $100 sign-up fee plus $25 per month
We need to write an equation for the cost (y) based on the number of months.
To solve the above problem, the answer is;a. y = 25x + 100
Explanation; Let's break down the problem
The $100 sign-up fee is a fixed cost that is added only once to the monthly fee which is $25. Thus the equation for the cost (y) based on the number of months can be expressed as; y = 25x + 100 where:y is the cost for the number of monthsx is the number of months
Therefore the correct answer is option A which is;y = 25x + 100.
To know more about equation visit:
https://brainly.com/question/29174899
#SPJ11
To join a local square dancing group,
Jan has to pay a $100 sign-up fee plus $25 per month.
The equation for the cost (y) based on the number of months is
y = 25x + 100,
where x is the number of months.
Option A is the correct equation for the cost based on the number of months.
Writing the equation:
y = 25x + 100
Where:
y = Cost based on the number of months
x = Number of months
Therefore, when Jan has been part of the local square dancing group for 1 month, the total cost will be:
$25 * 1 + $100 = $125
And if Jan has been a part of the group for 4 months, then the total cost would be:
$25 * 4 + $100 = $200
Therefore, option A is the correct answer.
To know more about number, visit:
https://brainly.com/question/3589540
#SPJ11
Assume that there is a statistically significant bivariate relationship between the amount of texting during driving and the number of accidents. Scientists later investigate whether or not this bivariate relationship is moderated by age.
Age 16-20: r = 0.6 p = 0.01
Age 21+: r = 0.2 p = 0.05
T or F: Based only on the r and p values listed above you can come to the conclusion that age is a moderator of the bivariate relationship between the amount of texting and the number of accidents.
Answers
It is False that based only on the r and p values listed above you can come to the conclusion that age is a moderator of the bivariate relationship between the amount of texting and the number of accidents.
In the given scenario, it is not completely true that based only on the r and p values listed above, you can come to the conclusion that age is a moderator of the bivariate relationship between the amount of texting and the number of accidents.
Let's first understand what is meant by the term "moderator.
"Moderator: A moderator variable is a variable that changes the strength of a connection between two variables. If there is a statistically significant bivariate relationship between the amount of texting during driving and the number of accidents, scientists investigate whether this bivariate relationship is moderated by age.
Therefore, based on the values of r and p, it is difficult to determine if age is a moderator of the bivariate relationship between the amount of texting and the number of accidents.
As we have to analyze other factors also to determine whether the age is a moderator or not, such as the sample size, the effect size, and other aspects to draw a meaningful conclusion.
So, it is False that based only on the r and p values listed above you can come to the conclusion that age is a moderator of the bivariate relationship between the amount of texting and the number of accidents.
To know more about values visit :
https://brainly.com/question/30145972
#SPJ11
(3.56)^2=30.91 true or false
Answers
Answer:
it is False
Step-by-step explanation:
12.6736≠30.91
Answer:
it is false
Step-by-step explanation:
because (3.56)^2= 3.56^2 = ( 89/25) ^2= 7621/625
What is the range of the function?

Answers
***HOPE This Help You***
Emma is designing a playground for her neighborhood
park. Her drawing has a scale of 1 cm: 3 feet. The length
of her drawing is 15 cm. What will be the actual lenght of
the playground in feet?
Answers
Answer: 45 feet
Answer:
45 feet
Step-by-step explanation:
if 1 cm = 3 ft, we can scale up the drawing from there.
We are multiplying each cm by 3, and considering that length to be 3 feet.
If we had 2 cm, (multiply both by 3) we would have 6 feet.
So, if we had 15 cm, we also need to convert this scale length into actual length. We do this by multiplying
15 × 3 = 45
So, we know that the actual length of the playground in feet is 45 feet.
Question 7 of 10
An object in geometry with no width, length or height is a(n):
A. line
ОО
B. ray
C. point
D. angle
SUBMIT
Answers
Answer:
A (point) is the answer to the question.
Evaluate the following integral using the trapezoidal rule (use only one interval) and Gauss- Quadrature (n=2). Compare your results with the exact values. Take gp1=-gp2 = 0.5773 and w1 = w2 = 1. 1 = ₀∫π/² Sin²x dx Exact: x/2 – sin(2x)/4
Answers
The given integral is ₁∫₀^(π/2) sin²(x)dx.
The trapezoidal rule is given by:(b - a) [(f(a) + f(b))/2]And, the Gauss-Quadrature formula for n = 2 is: ∫ᵇₐ f(x) dx = (b - a) [ w₁ f( [ (b - a)/2 ] gp₁ + (b + a)/2 ) + w₂ f( [ (b - a)/2 ] gp₂ + (b + a)/2 ) ]
Here, a = 0, b = π/2, gp₁ = -0.5773, gp₂ = 0.5773, w₁ = w₂ = 1.
(i) Trapezoidal Rule: The trapezoidal rule with one interval is given by:(b - a) [(f(a) + f(b))/2] = π/4 [sin²(0) + sin²(π/2)] = 0.7854
(ii) Gauss-Quadrature: Using the Gauss-Quadrature formula with n = 2, we get:∫ᵇₐ f(x) dx = (b - a) [ w₁ f( [ (b - a)/2 ] gp₁ + (b + a)/2 ) + w₂ f( [ (b - a)/2 ] gp₂ + (b + a)/2 ) ]= π/2 [ sin²( [ (π/2)/2 ] (-0.5773) + π/4 ) + sin²( [ (π/2)/2 ] (0.5773) + π/4 ) ]= 0.7853Comparing the above two methods, the trapezoidal rule and Gauss-Quadrature method are nearly the same and are close to the exact value.
Exact value = (π/2)/2 - sin(π)/4 = 0.7854Conclusion:Thus, it can be concluded that the given integral using the trapezoidal rule (using only one interval) and Gauss- Quadrature (n=2) is approximately equal to 0.7854.
To know more about integral visit
https://brainly.com/question/31433890
#SPJ11
please help i really need it and please don't answer just to guess please i really need the help this is the only one

Answers
Answer:
18x
Step-by-step explanation:
-It is the same as 3x^-2 • 6x^3.
-Multiply the constants (in this case 3 and 6 =18)
-Add the exponents (-2+3=1)
-Your answer is 18x
A baby alligator at the Henry Dooley zoo grew from 16 inches to 44 inches long in four months. Find the percent change. Is this percent increase or percent decrease
Answers
Answer:
increase in percent change
In February, Paul's electric bill was three dollars more then one-half his gas bill. If the electric bill was ninety-two dollars, what was the gas bill?
Answers
Answer:
49$
Step-by-step explanation:
b.
10 ft
C
3 ft
area of the rectangle =
area of the triangle =
Answers
Step-by-step explanation:
rectangle=l×w
10×3=30ft
triangle=b×h/2
10×3/2
30/2
=15ft
5. 50)700
Can u help me with this I don’t understand
Answers
Answer:
Step-by-step explanation:
1. Simplify the expression
2. Find the greatest common factor of the numerator and denominator ( divide)
(1.50)/ (14.50)
3. Factor out and cancel the greatest common factor
Answer is 1/14
find the value of e(|z|), where z is a standard normal variable.
Answers
To find the value of e(|z|), where z is a standard normal variable, we first need to determine the probability density function of |z|.
Let Y = |Z|, where Z is a standard normal variable. Then:
P(Y ≤ y) = P(|Z| ≤ y) = P(-y ≤ Z ≤ y) = Φ(y) - Φ(-y)
where Φ is the cumulative distribution function of the standard normal distribution.
The probability density function of Y can be obtained by differentiating the cumulative distribution function:
f_Y(y) = d/dy (Φ(y) - Φ(-y))
= φ(y) + φ(-y)
= 2φ(y)
where φ is the probability density function of the standard normal distribution.
Therefore, the expected value of |Z| is given by:
E(|Z|) = ∫₀^∞ y f_Y(y) dy
= 2 ∫₀^∞ y φ(y) dy
= 2 ∫₀^∞ (1/√(2π)) y e^(-y²/2) dy (using the standard normal density function)
This integral can be evaluated using integration by substitution, with u = y²/2 and du/dy = y. Thus:
E(|Z|) = 2 ∫₀^∞ (1/√(2π)) e^(-u) du
= 2/√(2π) * [ -e^(-u) ]_0^∞
= 2/√(2π)
= √(2/π)
Therefore, e(|z|) = √(2/π) ≈ 0.7979.
For more questions like variable visit the link below:
https://brainly.com/question/14439232
#SPJ11