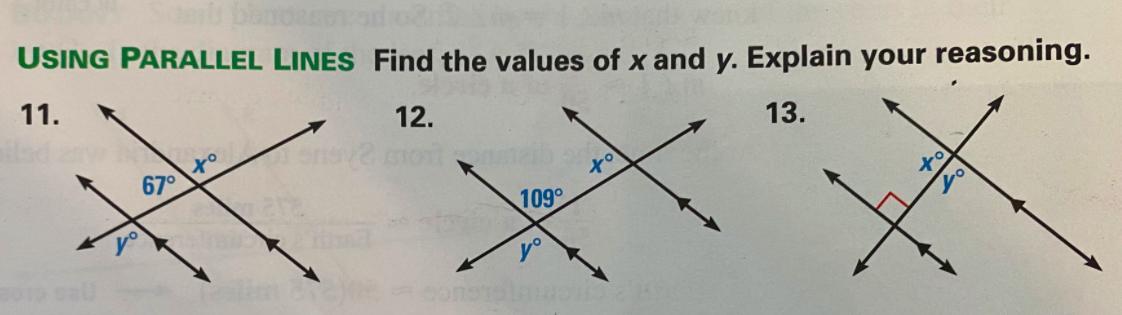Answers
Answer:
11. y and x would both be 113°
12. y would be 109° and x would be 71°
13. y and x would both be 90°
Related Questions
Write an equation for the line on the graph below:

Answers
Answer:
y=2
Step-by-step explanation:
Hey there!
The answer is y=2 because the x-axis is not defined (there's no value for it as the line didn't pass through it)
What is the probability that a flight between new york city and chicago is less than 140 minutes?
Answers
The probability that a flight takes more than 140 minutes is approximately 0.333. (Option d: P(x > 140) = 0.333)
To find the probability that a flight takes more than 140 minutes, we need to calculate the proportion of the total distribution that lies beyond 140 minutes.
Given that the time to fly is uniformly distributed between 120 and 150 minutes, we can determine the length of the entire distribution as:
Length of distribution = maximum time - minimum time = 150 - 120 = 30 minutes.
The proportion of the distribution that lies beyond 140 minutes can be calculated as:
Proportion = (Length of distribution - Length up to 140 minutes) / Length of distribution
= (30 - (140 - 120)) / 30
= (30 - 20) / 30
= 10 / 30
= 1/3
≈ 0.333
Therefore, the probability that a flight takes more than 140 minutes is approximately 0.333.
Hence, the correct option is:
d) P(x > 140) = 0.333
To know more about probability, refer here:
https://brainly.com/question/15157031
#SPJ4
Complete Question:
The time to fly between New York City and Chicago is uniformly distributed with a minimum of 120 minutes and a maximum of 150 minutes.
What is the probability that a flight takes time more than 140 minutes? *
a-P(x> 140)=0.14
b-P(x> 140)=1.4
c-P(x> 140)=0
d-P(x> 140) = 0.333
35 more than a number x is 73
Answers
Answer:
38
Step-by-step explanation:
X+35=73
x=73-35
x=38
Answer:
X=38
Step-by-step explanation:
x+35=73
-35 -35
Use cylindrical coordinates to evaluate the triple integral ∫∫∫Ex2+y2√dV
Answers
We know that if once you have the limits, you can substitute them into the integral and evaluate it accordingly.
To use cylindrical coordinates to evaluate the triple integral ∫∫∫E(x^2+y^2)^(1/2)dV, first recall the transformation from Cartesian coordinates (x, y, z) to cylindrical coordinates (ρ, θ, z):
x = ρcos(θ)
y = ρsin(θ)
z = z
The Jacobian for this transformation is |d(x, y, z)/d(ρ, θ, z)| = ρ. Thus, we can rewrite the integral as follows:
∫∫∫E(x^2+y^2)^(1/2)dV = ∫∫∫Eρ√(ρ^2cos^2(θ)+ρ^2sin^2(θ))ρdρdθdz
Simplify the expression under the square root:
ρ√(ρ^2cos^2(θ)+ρ^2sin^2(θ)) = ρ√(ρ^2(cos^2(θ)+sin^2(θ))) = ρ√(ρ^2) = ρ^2
Now, the triple integral becomes:
∫∫∫Eρ^2ρdρdθdz
Determine the limits of integration based on the given region. Without further information about the region, I cannot provide the exact limits of integration or evaluate the integral. However, once you have the limits, you can substitute them into the integral and evaluate it accordingly.
To know more about limits refer here
https://brainly.com/question/8533149#
#SPJ11
Which of the following best describes ethics?
it is a set of thoughts that are made about kinds of individuals
or their manners of conducting activities
it is a set of values that define r
Answers
Answer:
the second
Step-by-step explanation:
refers to well-founded standards of right and wrong that prescribe what humans should do, usually in terms of rights, obligations, benefits to society, justice
Question 3 The Schwarzschild metric is given by 2M 2M ds² -(₁-²M) di² + (1-²¹)- 1- dr² +r² (d0² + sin² 0 dó²). There are Killing vectors associated with time invariance and angular momen- tum invariance in the direction in this geometry leading to the conserved quantities e = (1-2) and l= r² sin² 0 dr From this one can derive an analog to the radial energy equation in Newtonian mechanics by orienting the coordinates so that the orbits are confined to the equatorial plane where 0 = π/2 and u = 0. One finds 2 1 dr + Veff (r) = E 2 dr (e²_ -1) where E = and Veft(r) = - + 2/²/²2 - Mp³². Further, for circular orbits one can show that M | [₁ + √/₁−12 (+1)]. r+= | 2M Finally, for circular orbits of radius R do 1/2 M dt R³ (a) Which value of r corresponds to the Schwarzschild radius of stable circular orbits: r or r? Justify your answer. [3 marks] (b) Show that for circular orbits of radius R do 1/2 M -1/2 3M (²) ¹² (1-³) dT R³ R where is the proper time. [6 marks] (c) A free particle is moving in a circular orbit around a spherical source of curvature of mass M. The Schwarzschild radius of the orbit is 8M. Use the equivalence principle to argue that the period as measured at infinity should be larger than that measured by the particle. [4 marks] (d) Find the period of the orbit as measured by an observer at infinity. Find the period of the orbit as measured by the particle. [7 marks] M
Answers
(A) Circular orbits of stable particles are possible at radii greater than three times the Schwarzschild radius for the non-rotating spherically symmetric mass.
This represents the radius of a black hole's event horizon, within which nothing can escape. The Schwarzschild radius is the event horizon radius of a black hole with mass M.
M can be calculated using the formula: r+ = 2Mwhere r+ is the radius of the event horizon.
(B) 1/2 M -1/2 3M (²) ¹² (1-³) dT = R³ R. This is the required expression.
Tau is the proper time of the particle moving around a circular orbit. Hence, by making use of the formula given above:1/2 M -1/2 3M (²) ¹² (1-³) dT = R³ dt.
(C) Time passes differently in different gravitational fields, and it follows that the period as measured at infinity should be larger than that measured by the particle.
The principle of equivalence can be defined as the connection between gravitational forces and the forces we observe in non-inertial frames of reference. It's basically the idea that an accelerating reference frame feels identical to a gravitational force.
(D) The period of the orbit as measured by an observer at infinity is 16π M^(1/2) and the period of the orbit as measured by the particle is 16π M^(1/2)(1 + 9/64 M²).
The period of orbit as measured by an observer at infinity can be calculated using the formula: T = 2π R³/2/√(M). Substitute the given values in the above formula: T = 2π (8M)³/2/√(M)= 16π M^(1/2).The period of the orbit as measured by the particle can be calculated using the formula: T = 2π R/√(1-3M/R).
Substitute the given values in the above formula: T = 2π (8M)/√(1-3M/(8M))= 16π M^(1/2)(1 + 9/64 M²).
To know more about Schwarzschild radius
https://brainly.com/question/29534114
#SPJ11
what is this pls help me 54 point to whoever helps me

Answers
Answer:
3 1/5
Step-by-step explanation:
help me on this questioj pelase

Answers
Answer:
A
A
Step-by-step explanation:
8) because of the rules of angles we know that all angles found on a line are equal to 180 degrees, and all angles opposite one another are equal. because of this A is not possible. 90 and 40 do not add up to 180 degrees, and are not equivalent to each other.
9) using the same rules as above, we know that the two angles have to add up to 180 degrees (they can't be equal this time). A is not possible.
Refer to Table S6.1 - Factors for Computing Control Chart Limits (3 sigma) for this problem. A quality inspector took the following samples of the length of time (in seconds) for glue to dry. Please round your calculations to three decimal places. Sample 1 Obs. 1 125 Obs. 3 122 Obs. 2 126 100 155 Obs. 4 132 121 118 Obs. 5 114 125 142 2 130 110 140 129 3 a) What is the value of ? x = seconds (round your response to three decimal places). b) What is the value of R? R= seconds (round your response to three decimal places). c) What are the UCL, and LCL, using 3-sigma? Upper Control Limit (UCL;) = seconds (round your response to three decimal places). Lower Control Limit (LCL;) = seconds (round your response to three decimal places). d) What are the UCLR and LCLR using 3-sigma? Upper Control Limit (UCLR) = seconds (round your response to three decimal places). Lower Control Limit (LCLR) = seconds (round your response to three decimal places).
Answers
To find the value of x, we calculate the average of the sample observations. Summing up the observations and dividing by the total number of observations, we get:
x = (125 + 122 + 126 + 100 + 155 + 132 + 121 + 118 + 114 + 125 + 142 + 2 + 130 + 110 + 140 + 129 + 3) / 17 = 114.118 seconds (rounded to three decimal places).b) To find the value of R, we calculate the range of each sample by subtracting the minimum observation from the maximum observation. Then we find the average range across all samples:R = (155 - 100 + 142 - 2 + 140 - 110 + 132 - 114 + 142 - 3) / 5 = 109.2 seconds (rounded to three decimal places).
c) The Upper Control Limit (UCL) and Lower Control Limit (LCL) using 3-sigma can be calculated by adding and subtracting three times the standard deviation from the average:UCL = x + (3 * R / d2) = 114.118 + (3 * 109.2 / 1.693) = 348.351 seconds (rounded to three decimal places).LCL = x - (3 * R / d2) = 114.118 - (3 * 109.2 / 1.693) = -120.115 seconds (rounded to three decimal places).
d) The Upper Control Limit Range (UCLR) and Lower Control Limit Range (LCLR) using 3-sigma can be calculated by multiplying the average range by the appropriate factor:UCLR = R * D4 = 109.2 * 2.115 = 231.108 seconds (rounded to three decimal places).LCLR = R * D3 = 109.2 * 0 = 0 seconds.
To learn more about observations click here : brainly.com/question/9679245
#SPJ11
The probability that an event will occur is fraction 1/8. Which of these best describes the likelihood of the event occurring?
Likely
Certain
Unlikely
Impossible
Answers
Answer:
Unlikely
Step-by-step explanation:
Certain= 100% chance of your event occuring.
Impossible = 0% chance of your event occuring.
Neither of these apply.
Likely= >50% = >4/8
Unlikely= <50% = <4/8
Unlikely
If the slope of a line is 2 and the y-intercept is 7, what would the equation be in slope intercept form?
Question 11 options:
y = 7x + 2
y = -2x -7
y = 2x -7
y= 2x + 7
Answers
Answer:
y = 2x+7
Step-by-step explanation:
y = mx + c
m = slope
c is the y intercept
so
y = 2x+ 7
Write an equation in slope-intercept form (y=mx+b) of the line that passes through (2,3) and (0,7)
Answers
if 26 children were to be born in a hospital on a given day, how many combinations of 6 boys and 20 girls would exist? 230,230 4 x 10^26 500,000 15 Z
Answers
The number of combinations of 6 boys and 20 girls that can exist among 26 children born in a hospital on a given day is 230,230.
]To calculate the number of combinations, we can use the concept of binomial coefficients. The formula for calculating the number of combinations is C(n, k) = n! / (k!(n-k)!), where n is the total number of objects and k is the number of objects we want to select.
In this case, we have 26 children in total, and we want to select 6 boys and 20 girls. Plugging these values into the formula, we get C(26, 6) = 26! / (6!(26-6)!) = 230,230. Therefore, there are 230,230 different combinations of 6 boys and 20 girls that can exist among the 26 children born in the hospital on that given day.
Learn more about combinations here : brainly.com/question/28065038
#SPJ11
Please help me with algebra. I’m stuck.

Answers
Answer:
the answer to question 18 is
6n- 2n = 4n
4n=4
divide both side by 4
4÷4= 1
so the answer is 1
Each of a company's 546 employees earns $790 each week. What is the total
amount the company pays all its employees for 4 weeks?
Answers
Answer:
$1,725,360
Step-by-step explanation:
For this, you would just multiply every number: \(employees×weekly salary×weeks\) which is \(546×790×4=1,725,360\).
Answer:
I think all u need to do is mulitply thoses numbers just use calulator
Step-by-step explanation:
hope it helped
what is the value of the five? 5,409.367
Answers
Answer: 5,000
hope this helps
Answer:
5 thousand would be the answer
Step-by-step explanation:
the 5 is in the thousandths place
The following table shows the number of candy bars bought at a local grocery store and the
total cost of the candy bars:
Candy Bars: 3, 5, 8, 12, 15, 20, 25
Total Cost: $6.65, $10.45, $16.15, $23.75, $29.45, $38.95, $48.45
If B represents the number of candy bars purchased and C represents the total cost of the candy bars, write the linear model that models the cost of any number of candy bars.
Answers
The linear model that represents the cost of any number of candy bars can be written as: C = $1.90B + $0.95
To write the linear model that models the cost of any number of candy bars, we need to find the equation of a line that best fits the given data points. We'll use the variables B for the number of candy bars purchased and C for the total cost of the candy bars.
Looking at the given data, we can see that there is a linear relationship between the number of candy bars and the total cost. As the number of candy bars increases, the total cost also increases.
To find the equation of the line, we need to determine the slope and the y-intercept. We can use the formula for the equation of a line: y = mx + b, where m is the slope and b is the y-intercept.
First, let's find the slope (m) using two points from the given data, for example, (3, $6.65) and (25, $48.45):
m = (C2 - C1) / (B2 - B1)
= ($48.45 - $6.65) / (25 - 3)
= $41.80 / 22
≈ $1.90
Now, let's find the y-intercept (b) using one of the data points, for example, (3, $6.65):
b = C - mB
= $6.65 - ($1.90 * 3)
= $6.65 - $5.70
≈ $0.95
Therefore, the linear model that represents the cost of any number of candy bars can be written as:
C = $1.90B + $0.95
This equation represents a linear relationship between the number of candy bars (B) and the total cost (C). For any given value of B, you can substitute it into the equation to find the corresponding estimated total cost of the candy bars.
for more such question on linear visit
https://brainly.com/question/2030026
#SPJ8
In which quadrant does 0 lie if the following statements are true:
csc 0 >0 and cos 0 <0
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
Answers
The answer is Quadrant II. First, we need to understand what csc and cos represent in trigonometry. Csc (cosecant) is the reciprocal of sine, meaning it is equal to 1/sin.
Cos (cosine) represents the ratio of the adjacent side of a right triangle to its hypotenuse.
Now, let's look at the given statements. csc 0 > 0 means that the sine of 0 is positive. Since sine is positive in Quadrants I and II, we know that 0 lies in either of those two quadrants.
Next, cos 0 < 0 means that the cosine of 0 is negative. Since cosine is negative in Quadrants II and III, we can eliminate Quadrant I as a possibility and conclude that 0 must lie in Quadrant II.
Based on the given conditions, csc θ > 0 and cos θ < 0, θ lies in Quadrant II.
Explanation:
csc θ is positive when sin θ is positive. Sin θ is positive in Quadrant I and II.
cos θ is negative in Quadrant II and III.
The only common quadrant is Quadrant II.
To know more about trigonometry visit:-
https://brainly.com/question/29002217
#SPJ11
In the square below, the diagonal AC is 12v2 inches Find the area of the shaded region and find the exact circumference of the inscribed © X.
Answers
AB = BC
\(\begin{gathered} (AC)^2=(AB)^2+(BC)^2 \\ (12\sqrt[]{2})^2=(BC)^2+(BC)^2 \end{gathered}\)\(\begin{gathered} 24=2(BC)^2 \\ \frac{24}{2^{}}=(BC)^2\text{ } \\ (BC)^2=12 \\ BC\text{ =}\sqrt[]{12} \\ BC\text{ = 2}\sqrt[]{3}\text{ inches} \end{gathered}\)Area of shaded part = Area of the square - the area of the circle
\(\begin{gathered} \text{Area of square = length x length} \\ \text{Area of square = 2}\sqrt[]{3}\times2\sqrt[]{3}=12inch^2 \end{gathered}\)\(\begin{gathered} \text{Area of circle = }\pi\text{ }\times r^2 \\ r=\text{ BC = 2}\sqrt[]{3}inches \\ \text{Area of circle= 3.14 }\times(2\sqrt[]{3)}^2=\text{ 37.68} \end{gathered}\)Area of shaded part = 37.68- 12 =25.68 square inche
\(\text{Circumference of a circle = 2}\times\pi\times r\)\(undefined\)
Given: BC bisects ZABD
mZABD = 52°
Prove: mABC = 26°
A
D
B
Assemble the proof by dragging tiles to
the Statements and Reasons columns.
Statements Reasons
mZABD = 52
mZABC+ m ZABC = 52
Statements
mZABC=mZCBD
m/ABC+mZC=52
Reasons
BC bisects ZABD
mZABC+mZCBD =
m ZABD

Answers
A bisector is a line that divides a given line or angle into two equal parts or measures. So that the required statements and reasons are given below:
STATEMENT REASONS
1. BC bisects <ABD Given
2. m<ABC = \(26^{o}\) Bisection property of an angle
3. 2(m<ABC) = \(52^{o}\) Sum of angles of a bisected angle
4. m<ABC = m<CBD Congruent parts of a bisected angle
5. <mABC + m<ABC = \(52^{o}\) Sum of an individual angle of a bisected angle
6. m<ABC + m<CBD = \(52^{o}\) Sum of angles of a bisected angle
7. m<ABC + m<CBD = m<ABD Sum of the angles of a bisected angle
The above statements and reasons are majorly centered on a bisector, the angles formed due to the bisection of a given angle, and the bisected angle.
For more clarifications on the bisection of an angle, visit: https://brainly.com/question/5799105
#SPJ1
Answer:
1. BC bisects <ABD | Given
2.m<ABD=52 | Given
3.m<ABC = m<CBD | Definition of Bisector
4.m<ABC + m<CBD = m<ABD | Angle Addition Postulate
5.m<ABC + m<CBD =52 | Substitution Property
6.m<ABC + m<ABC =52 | Substitution Propery
7.2(m<ABC)=52 | Addition
8.m<ABC=26 | Division Property
Step-by-step explanation:
Edge 2022
100 points & i'll give brainliest!
find the indicated intersection or union. express your answers in interval notation
(-1,1) U [0,6]
Answers
The first interval goes from -1 to 1 (not including either endpoint).
The second interval goes from 0 to 6 (including both endpoints).
So, the first one starts at -1 and keeps going to the right, overlapping where the second one picks up and you keep going until you get to 6.
You still need to leave out -1 and include 6.
Answer: (-1,6]
A roulette wheel consists of 38 slots, numbered 0, 00, 1, 2,. , 36. To play the game, a metal ball is spun around the wheel and allowed to fall into one of the numbered slots. The slots numbered 0 and 00 are green, the odd numbers are red, and the even numbers are black. (a) Determine the probability that the metal ball falls into a green slot. Interpret this probability. (b) Determine the probability that the metal ball falls into a green or a red slot. Interpret this probability. (c) Determine the probability that the metal ball falls into 00 or a red slot. Interpret this probability (d) Determine the probability that the metal ball falls into the number 31 and a black slot simultaneously. What term is used to describe this event? (a) P(green) = ___ (Type an integer or decimal rounded to four decimal places as needed. ) If the wheel is spun 100 times, one would expect about __ spin(s) to end with the ball in a green slot. (Round to the nearest integer as needed. ) (b) P(green or red) = ___
(Type an integer or decimal rounded to four decimal places as needed. ) If the wheel is spun 100 times, one would expect about __ spin(s) to end with the ball in either a green or red slot. (Round to the nearest integer as needed. ) (c) P(00 or red)= ___ (Type an integer or decimal rounded to four decimal places as needed. )
Answers
(a). There is a 5.26% chance that the metal ball falls into a green slot.
(b). There is a 52.63% chance that the metal ball falls into either a green or a red slot on any given spin of the roulette wheel.
(c). P(00 or red) ≈ 0.5263
(d). This event is called impossible.
(a) P(green) = 2/38 = 1/19 ≈ 0.0526.
This means that there is a 5.26% chance that the metal ball falls into a green slot on any given spin of the roulette wheel.
If the wheel is spun 100 times, one would expect about 5 spins to end with the ball in a green slot. (Expected value = 100 x P(green) = 100/19 ≈ 5.26, which we round to the nearest integer.)
(b) P(green or red) = P(green) + P(red) = 2/38 + 18/38 = 20/38 ≈ 0.5263. This means that there is a 52.63% chance that the metal ball falls into either a green or a red slot on any given spin of the roulette wheel.
If the wheel is spun 100 times, one would expect about 53 spins to end with the ball in either a green or red slot. (Expected value = 100 * P(green or red) = 2000/38 ≈ 52.63, which we round to the nearest integer.)
(c) P(00 or red) = P(00) + P(red) = 2/38 + 18/38 = 20/38 ≈ 0.5263. This means that there is a 52.63% chance that the metal ball falls into either 00 or a red slot on any given spin of the roulette wheel.
(d) The probability that the metal ball falls into the number 31 and a black slot simultaneously is zero, since 31 is an odd number and all odd numbers are red on the roulette wheel. This event is called impossible.
To learn more about the probability;
brainly.com/question/11234923
#SPJ1
Find the area of the Trapezoid
6.2 yd
5.6 yd
4 yd
13.4 yd
please explain I'll mark brainlisest

Answers
Area of trapezoid= 1/2 (13.4+5.6)×4
= 1/2 ×19
=76/2
=38yd

An assembly line has 16 hours to make 1.000 units. What is the required cycle time? (slide 23) 72sec 216sec 57.65sec 14,4sec
Answers
The required cycle-time is approximately 57.6 seconds.
To find the required cycle time, we need to divide the total available time by the number of units to be produced.
Total available time: 16 hours = 16 * 60 minutes = 960 minutes = 960 * 60 seconds = 57,600 seconds
Number of units to be produced: 1,000 units
Required cycle time: Total available time / Number of units
Cycle time = 57,600 seconds / 1,000 units
Cycle time ≈ 57.6 seconds
Therefore, the required cycle time is approximately 57.6 seconds.
Learn more about cycle-time from the given link
https://brainly.com/question/15356513
#SPJ11
x^100+1 divide by x+1
Answers
Answer:
x=-1
Step-by-step explanation:
\( \frac{x ^{100} + 1 }{x + 1} \)
\(x + 1 = 0\)
\(x = - 1\)
the half-life of chromium-51 is 38 days. If the sample contained 510 grams. How much would remain after 1 year?
Answers
Answer:
About 0.6548 grams will be remaining.
Step-by-step explanation:
We can write an exponential function to model the situation. The standard exponential function is:
\(f(t)=a(r)^t\)
The original sample contained 510 grams. So, a = 510.
Each half-life, the amount decreases by half. So, r = 1/2.
For t, since one half-life occurs every 38 days, we can substitute t/38 for t, where t is the time in days.
Therefore, our function is:
\(\displaystyle f(t)=510\Big(\frac{1}{2}\Big)^{t/38}\)
One year has 365 days.
Therefore, the amount remaining after one year will be:
\(\displaystyle f(365)=510\Big(\frac{1}{2}\Big)^{365/38}\approx0.6548\)
About 0.6548 grams will be remaining.
Alternatively, we can use the standard exponential growth/decay function modeled by:
\(f(t)=Ce^{kt}\)
The starting sample is 510. So, C = 510.
After one half-life (38 days), the remaining amount will be 255. Therefore:
\(255=510e^{38k}\)
Solving for k:
\(\displaystyle \frac{1}{2}=e^{38k}\Rightarrow k=\frac{1}{38}\ln\Big(\frac{1}{2}\Big)\)
Thus, our function is:
\(f(t)=510e^{t\ln(.5)/38}\)
Then after one year or 365 days, the amount remaining will be about:
\(f(365)=510e^{365\ln(.5)/38}\approx 0.6548\)
A dentist bought 9 bags of prizes for his patients. Each bag had 12 prizes. The prizes were divided equally among 3 boxes. How many prizes were in each box?
Answers
Answer:
36
Step-by-step explanation:
A dentist bought 9 bags of prizes for his patients.
Each of the bags has 12 prizes
The first step is to calculate the total number of prizes
= 9 × 12
= 108 prizes
Since the prizes will be shared equally in 3 boxes then the number of prizes in each box can be calculated as follows
= 108/3
= 36
Hence the number of prizes in each of the 3 boxes is 36
A person is riding a bicycle along a straight highway.
The graph at the right shows the rider's distance y in miles from a First Aid Station after x
hours.
(a) Find the slope-intercept form of the equation of the line.

Answers
Answer:
y=28/3x+6
Step-by-step explanation:
If you use the slope formula, y2-y1
_____\
x2-x1
You would get that the slope is 23/3 and you can see the y-intercept is 6 so you would get y=28/3x+6.
The angle of elevation of the top of the building at a distance of 50m from its foot on a horizontal plane is found to be 60 degrees. Find the height of the building
Answers
The height of the building is approximately 86.60 meters.
To find the height of the building, we can use trigonometric ratios, specifically the tangent function.
In this scenario, the angle of elevation is 60 degrees, and the distance from the foot of the building to the point where the angle is measured is 50 meters.
Let's denote the height of the building as 'h'. According to trigonometry, the tangent of an angle is equal to the ratio of the opposite side to the adjacent side.
In this case, the opposite side is the height of the building (h), and the adjacent side is the distance from the foot of the building (50 meters).
Using the tangent function, we have:
tan(60 degrees) = h/50
Simplifying this equation, we can solve for h:
h = 50 × tan(60 degrees)
Using a scientific calculator or trigonometric table, we find that tan(60 degrees) is approximately 1.732.
Therefore, h = 50 × 1.732 ≈ 86.60 meters.
For more questions on height
https://brainly.com/question/31485233
#SPJ8
A football coach is trying to decide: When a team is ahead late in the game,
which strategy is better?
Play the "regular" defense.
Play a "prevent" defense that guards against long gains but makes short
gains easier.
The coach reviews the outcomes of 100 games.
Win
Loss
Total
Regular defense
42
8
50
Prevent defense
35
15
50
Total
77
23
100
Compare the probability of winning when playing regular defense with the
probability of winning when playing prevent defense. Draw a conclusion
based on your results.
Answers
You are more likely to win by playing regular defense.
What is probability?The probability of an event is a number that indicates how likely the event is to occur. It is expressed as a number in the range from 0 and 1, or, using percentage notation, in the range from 0% to 100%. The more likely it is that the event will occur, the higher its probability.
Assume out of 100 reviewed games, there were 50 regular defense games and 50 prevent defense games. And out of 50 regular defense games, 38 were won, 12 were lost.
And out of 50 prevent defense game, 29 were won, 21 were lost.
Probability to win the game by playing regular defense is:
P(win | regular) = 38/50 = 0.76
Probability to win the game by playing prevent defense is:
P(win | prevent) = 29/50 = 0.58
Since the probability of winning by regular defense game is more than prevent defense game (0.76 > 0.58),
Hence, you are more likely to win by playing regular defense.
Learn more about probability click;
https://brainly.com/question/30034780
#SPJ7