helpFind the fourth derivative of f(x) = 2 + In (2) - 179x Enclose arguments of functions in parentheses For example, sin (2x).
Answers
The fourth derivative of f(x) is simply 0.
How to find the fourth derivative?To find the fourth derivative of f(x) = 2 + ln(2) - 179x, we need to first take the derivative of the function three times.
First derivative: f'(x) = -179
Second derivative: f''(x) = 0
Third derivative: f'''(x) = 0
Now, to find the fourth derivative, we need to take the derivative of f'''(x) with respect to x:
f''''(x) = 0
So the fourth derivative of f(x) = 2 + ln(2) - 179x is simply 0.
Note: The function sin(2x) was not necessary to find the fourth derivative of f(x).
Learn more about the fourth derivative.
brainly.com/question/31059058
#SPJ11
Related Questions
Help? please!
6³− 43.5 = 250.5
Answers
Answer:
172.2 = 250.5
Step-by-step explanation:
6³− 43.5 = 250.5
Follow PEMDAS (Parenthesis Exponents Multiplication Division Addition Subtraction)
216 − 43.5 = 250.5
172.2 = 250.5
Answer:
The answer is false.
6³− 43.5 ≠ 250.5
6³− 43.5 = 172.5
Step-by-step explanation:
I hope this helps.
AMSWER ASAP PLEASE PLEASE PLEASE

Answers
Answer:
(2,14)
Step-by-step explanation:
so i solved this with substitution but there are other methods to solve this!
equation 1 : y = -x + 16
equation 2 : y = x + 12
solve for y in equation 1 !!
y = -x + 16
(add x on both sides)
y + x = 16
(subtract y on both sides)
x = -y + 16
equation 1 now equals : x = -y + 16
substitute equation 1 into equation 2 :)
y = (-y + 16) + 12
(add 16 + 12)
y = -y + 28
(add y on both sides)
2y = 28
(divide 2 on both sides)
y = 14
now to solve for x you can insert y !
you can use equation 1 or equation 2 to solve for x.
i'm using equation 2 :
y = x + 12
(14) = x + 12
(subtract 12 on both sides)
x = 2
therefore, the answer is (2, 14).
hope this helps :p
Which of the following phrases represents the algebraic expression 3x + 4?
The answers:
The sum of three and a number and four
The sum of three times a number and four
The product of three and a number and four
Four more than the sum of three and a number
Answers
Answer:
the answer is the product of 3 and 4 because 3x is a multipulcation problem
can someone please help me:(

Answers
The equation, (x - 10)² + (y - 5)² = 144, represents a circle with center (10, 5) and radius 12.
Determining the center and radius of a circleFrom the question, we are to determine the center and radius of the circle represented by the given equation
From the given information, the given equation is
(x - 10)² + (y - 5)²= 144
To determine the center and the radius of the circle we will compare the given equation to the standard form of the equation of a circle:
(x - h)² + (y - k)² = r²
where (h, k) is the center of the circle and r is the radius.
The equation
(x - 10)² + (y - 5)²= 144
can be written as
(x - 10)² + (y - 5)²= 12²
By comparison,
h = 10, k = 5 and r = 12
Hence, the center of the circle is (10, 5) and the radius is 12
Learn more on Determining the center and radius of a circle here: https://brainly.com/question/26757548
#SPJ1
Question attached through files! Can anyone help?? Thank you!

Answers
Answer:
(-1.732,0) and (1.732,0)
Step-by-step explanation:
Ignore f(x). The solutions are also called x-intercepts and zeros. So the solutions would be where the parabola crosses the x axis. In my answer ignore the 0 in the coordinates. Just put in the -1.732 and 1.732.
i really need to know this or imma fail!!!!!!!

Answers
The answer to the simplified expression 4⁹/4³ in index form is derived to be equal to 4⁶
How to simplify fraction of numbers in index formTo simplify a fraction written in index form, you can first express the numbers in prime factorization form by writing both the numerator and denominator as a product of prime factors. Identify common prime factors in the numerator and denominator and cancel them out. Then write the remaining factors as a product in index form.
Given the fraction 4⁹/4³, we can simplify as follows:
4⁹/4³ = (4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4)/(4 × 4 × 4)
we can cancel out (4 × 4 × 4) from both the numerator and denominator, living us with;
4⁹/4³ = 4 × 4 × 4 × 4 × 4 × 4
4⁹/4³ = 4⁶
Therefore, the answer to the simplified expression 4⁹/4³ in index form is derived to be equal to 4⁶
Read more about index here:https://brainly.com/question/15361818
#SPJ1
Which of the following algebraic represents shows a dilation that is an enlargement ?
Answers
The algebraic representation that shows a dilation that is an enlargement is (5/2 x,5/2 y). (Option D)
A dilation is a type of transformation that changes the size of the shape or object. It refers to a process of changing an object’s size by decreasing or increasing its dimensions by a scaling factor. A dilation produces an image that has the same shape as the original image but is a different size.
A dilation that results in a larger image is called an enlargement while a dilation that generates a smaller image is called a reduction. A dilation is described using the scale factor and the center of the dilation (which is a fixed point in the plane).
For a scale factor > 1, the image is an enlargement; for a scale factor < 1 and > 0, the image is a reduction; and for a scale factor = 1, the figure and the image are congruent. Hence, for a point (x,y), algebraic representation that shows a dilation that is an enlargement is (5/2 x,5/2 y) as the scale factor is greater than 1. For the remaining options, the scale factor is between 0 and 1, hence they are reduction.
Note: The question is incomplete. The complete question probably is: Which of the following algebraic representation shows a dilation that is an enlargement? A) (1/3 x,1/3 y) B) (0.1x, 0.1y) C) (5/6 x,5/6 y) D) (5/2 x,5/2 y)
Learn more about Dilation:
https://brainly.com/question/29449871
#SPJ4
can somebody help I am really bad at this

Answers
Answer:
40 feet
Step-by-step explanation:
4+4+8+4+12+8
= 40 ft.
Hudson and Knox are in a race. Hudson is running at a speed of 8. 8 feet per second. Knox got a 30-foot head start and is running at a speed of 6. 3 feet per second. How many seconds will it take until Hudson and Knox have run the same number of feet? Write the equation
Answers
It will take 12 seconds until Hudson and Knox have run the same number of feet.
Let's denote the time it takes until Hudson and Knox have run the same number of feet as "t" (in seconds).
The distance Hudson runs can be calculated by multiplying his speed (8.8 feet/second) by the time "t". Thus, the distance Hudson covers is 8.8t feet.
Knox, on the other hand, had a head start of 30 feet. So the distance Knox covers can be calculated by multiplying his speed (6.3 feet/second) by the time "t" and adding the head start of 30 feet. Thus, the distance Knox covers is 6.3t + 30 feet.
To find the time when both runners have covered the same distance, we set their distances equal to each other:
8.8t = 6.3t + 30
Simplifying the equation:
2.5t = 30
Dividing both sides by 2.5:
t = 30 / 2.5
t = 12
Therefore, it will take 12 seconds until Hudson and Knox have run the same number of feet.
Learn more about same number here
https://brainly.com/question/17060199
#SPJ11
16x+6=3x+3 sove for X
send help pls :'))
Answers
Answer: x = -3/13.
Step-by-step explanation: Start by subtracting 3x from both sides of the equation to isolate the x terms on one side:
16x + 6 - 3x = 3x + 3 - 3x
Simplifying the equation:
13x + 6 = 3
Next, subtract 6 from both sides of the equation:
13x + 6 - 6 = 3 - 6
Simplifying the equation:
13x = -3
Finally, divide both sides of the equation by 13 to solve for x:
(13x)/13 = (-3)/13
Simplifying the equation:
x = -3/13
How many natural numbers between $150$ and $300$ are divisible by $9$?
Answers
Answer:
There are 17 natural numbers divisible.
There are 17 natural numbers between 150 and 300 that are divisible by 9.
To find the number of natural numbers between 150 and 300 that are divisible by 9, we need to find the count of multiples of 9 within this range.
The first multiple of 9 greater than or equal to 150 is 153 (9 x 17), and the last multiple of 9 less than or equal to 300 is 297 (9 x 33).
Now, we can calculate the number of multiples of 9 between 153 and 297 (inclusive):
Number of multiples of 9 = (Last multiple - First multiple) / 9 + 1
Number of multiples of 9 = (297 - 153) / 9 + 1
Number of multiples of 9 = 144 / 9 + 1
Number of multiples of 9 = 16 + 1
Number of multiples of 9 = 17
So, there are 17 natural numbers between 150 and 300 that are divisible by 9.
Learn more about natural numbers click;
https://brainly.com/question/17273836
#SPJ3
Which of the following inequalities matches the graph?
answers:
x < 2
y > 2
y < 2
x > 2

Answers
Answer:
None of them but for the actual question on the picture it is x < -3
Step-by-step explanation:
For one month Siera calculated her home town’s average high temperature in degrees Fahrenheit. She wants to convert that temperature from degrees Fahrenheit to degrees Celsius using the function C of F = five-ninths (F minus 32) . What does C(F) represent?
the temperature of F degrees Fahrenheit converted to degrees Celsius
the temperature of F degrees Celsius converted to degrees Fahrenheit
the temperature of C degrees Fahrenheit converted to degrees Celsius
the temperature of C degrees Celsius converted to degrees Fahrenheit
{y | y = –7, –6, –2, –1, 0, 1, 3, 9}
Answers
For given average temperatures and °C=5/9°F-32 C represents temperature unit in celsius.
What is average?
In Maths, an average of a list of data is the expression of the central value of a set of data. Mathematically, it is defined as the ratio of summation of all the data to the number of units present in the list. In terms of statistics, the average of a given set of numerical data is also called mean. For example, the average of 2, 3 and 4 is (2+3+4)/3 = 9/3 =3. So here 3 is the central value of 2,3 and 4. Thus, the meaning of average is to find the mean value of a group of numbers.
Average = Sum of Values/Number of Values
Also
Suppose, we have given with n number of values such as x1, x2, x3 ,….., xn. The average or the mean of the given data will be equal to:
Average = (x1+x2+x3+…+xn)/n
Now,
Given formula
°C=5/9°F-32, C represents where °c is temperature unit in Celsius and
°F represents unit of temperature in Fahrenheit.
To know more about average visit the link
https://brainly.com/question/27193544?referrer=searchResults&source=aidnull
#SPJ1
To choose the three players fairly, Coach Bennet decides to set up a free throw contest. The three players who make the most consecutive free throws will get to go to the summer basketball clinic.
Part A
Question
How many different orders of top-three finishers are possible?
Answers
The number of different orders of top-three finishers in the free throw contest depends on the total number of participants. The specific number of participants is not provided in the given information.
To determine the number of different orders of top-three finishers, we need to know the total number of participants in the free throw contest. The order of finishers can be calculated using the concept of permutations, where the order matters.
If there are "n" participants, the number of different orders of top-three finishers can be calculated using the formula nP3, which represents the number of permutations of "n" objects taken 3 at a time. However, since the total number of participants is not provided in the given information, we cannot determine the exact number of different orders of top-three finishers.
To learn more about permutations click here:
brainly.com/question/29990226
#SPJ11
Q1. Consider the third-order linear homogeneous ordinary differential equa- tion with variable coefficients (2-x) d³y/dx³+ (2x-3). d²y/dy - x dy/dx +y=0, x < 2. da2 dx = First, given that y₁(x) = e is a solution of the above equation, use the method of reduction of order to find its general solution as yh (x)= Cif(x) + C2g(x) + C3h(x), where the functions f(x), g(x), h(x) must be explicitly determined. Now, consider the inhomogeneous ordinary differential equation 2-x) d³y/dx³+ (2x-3). d²y/dy - x dy/dx +y=(x-2)^2, x < 2. . dx² dx Let y(x) = u₁(x)f(x) + u₂(x)g(x) + u3(x)h(x) and use the method of variation of parameters to write down the three ordinary differential equations that must be satisfied by the first-order derivatives of the unknown functions u1, u2, u3. Find these functions by integration, and thus establish the particular solution yp(x) of the given inhomogeneous equation. [30 marks]
Answers
First, we use the method of reduction of order to find the general solution of the differential equation.
Given that y1(x) = e^x is a solution of the above equation, we want to find another solution y2(x) of the form y2(x) = u(x)e^x, where u(x) is an unknown function of x. We obtain the first and second derivatives of y2(x) as follows: y2(x) = u(x)e^x
dy2/dx = (u'(x) + u(x))e^x d²y2/dx² = (u''(x) + 2u'(x) + u(x))e^x.
Substituting y1(x) = e^x, y2(x), and their first two derivatives into the differential equation (2 - x)d³y/dx³ + (2x - 3)d²y/dx² - xdy/dx + y = 0, we get: (2 - x)[(u''(x) + 2u'(x) + u(x))e^x] + (2x - 3)[(u'(x) + u(x))e^x] - x[u(x)e^x] + u(x)e^x = 0.
Expanding the brackets and collecting like terms, we get: [u''(x) + (2 - x)u'(x) + (2x - 3)u(x)]e^x = 0.Since e^x ≠ 0 for all x, we can divide both sides by e^x to get: u''(x) + (2 - x)u'(x) + (2x - 3)u(x) = 0. This is a second-order linear homogeneous ordinary differential equation with variable coefficients, which we can solve using the method of undetermined coefficients.
We guess that u(x) = Ax + B, where A and B are constants to be determined. We obtain the first and second derivatives of u(x) as follows: u'(x) = A, u''(x) = 0. Substituting u(x), u'(x), and u''(x) into the differential equation, we get: 0 + (2 - x)A + (2x - 3)(Ax + B) = 0. Expanding the brackets and collecting like terms, we get: (2A - A)x + (4B - 3A) = 0. Equating the coefficients of x and the constant terms to zero, we get the following system of linear equations: 2A - A = 0, 4B - 3A = 0. Solving for A and B, we get: A = 0, B = 0. Therefore, u(x) = 0, and the general solution of the differential equation is: yh(x) = C1e^x. Now, we consider the inhomogeneous ordinary differential equation (2 - x)d³y/dx³ + (2x - 3)d²y/dx² - xdy/dx + y = (x - 2)², x < 2. We first find the general solution of the corresponding homogeneous equation, which is given by yh(x) = C1e^x. We then use the method of variation of parameters to find a particular solution yp(x) of the inhomogeneous equation of the form yp(x) = u1(x)e^x + u2(x)xe^x + u3(x)x²e^x, where u1(x), u2(x), and u3(x) are unknown functions of x to be determined. We obtain the first derivatives of u1(x), u2(x), and u3(x) as follows: du1/dx = -[p₂(x)y₂(x) + p₃(x)y₃(x)]yp/dx + f(x)/W(y1,y2,y3) du2/dx = [p₁(x)y₁(x) + p₃(x)y₃(x)]yp/dx - x f(x)/W(y1,y2,y3) du3/dx = -[p₁(x)y₁(x) + p₂(x)y₂(x)]yp/dx + x²f(x)/W(y1,y2,y3),
where p₁(x) = (2 - x),
p₂(x) = (2x - 3), p₃(x) = -x, and W(y1,y2,y3) is the Wronskian of
y1(x) = e^x, y2(x), and y3(x).
The Wronskian is given by W(y1,y2,y3) = e^x[y2(x)x² - y3(x)x + y3(x) - y2(x)]. Substituting y1(x) = e^x,
y2(x) = xe^x,
y3(x) = x²e^x,
and f(x) = (x - 2)² into the above equations, we get:
du1/dx = -(2 - x)xe^x(x²e^x)² + (x - 2)²/[(xe^x)
(x²e^x - x²e^x)] = -(2 - x)x(x²e^x) + (x - 2)²/
[x³e^x] du2/dx = (2x - 3)x²e^x(x²e^x)² - x(x - 2)²/[(e^x)
(x²e^x - x²e^x)] = (2x - 3)x²(x²e^x) - (x - 2)²/[xe^x] du3/dx = -x²e^xxe^x(x - 2)² + (x - 2)²/[e^x(x²e^x - xe^x)] = -x²(x - 2)² + (x - 2)²/[x(x - 1)].
Therefore, the first-order derivatives of u1(x), u2(x), and u3(x) are given by: du1/dx = -x³e^x(2 - x) + (x - 2)²/[x³e^x] du2/dx = 2x³e^x(2x - 3) - (x - 2)²/[xe^x] du3/dx = -(x - 2)² + (x - 2)²/[x(x - 1)].
Integrating these equations with respect to x, we get: u1(x) = (x - 2)³/6 - x² + C1 u2(x) = (x - 2)²/2 + x³ - C2
u3(x) = -x² + x - 2 + C3,
where C1, C2, and C3 are constants of integration. Therefore,
the particular solution of the inhomogeneous equation is given by: yp(x) = (x - 2)³/6 - x² + C1e^x + (x - 2)²/2 + x³ - C2xe^x - x² + x - 2 + C3x²e^x = (x - 2)³/6 + (x - 2)²/2 + x³ + (C1 - C2)x + (C3 - 1)x² - x²e^x.
Therefore, the general solution of the inhomogeneous equation is given by: y(x) = yh(x) + yp(x) = C1e^x + (x - 2)³/6 + (x - 2)²/2 + x³ + (C1 - C2)x + (C3 - 1)x² - x²e^x.
We are given the third-order linear homogeneous ordinary differential equation with variable coefficients as(2-x) d³y/dx³+ (2x-3). d²y/dy - x dy/dx +y=0, x < 2.
We are to find the general solution using the method of reduction of order. Given that y₁(x) = e^x is a solution of the above equation, we want to find another solution y₂(x) of the form y2(x) = u(x)e^x, where u(x) is an unknown function of x. We obtain the first and second derivatives of y2(x) as follows:y2(x) = u(x)e^x.
To know more about differential visit:
https://brainly.com/question/31383100
#SPJ11
Mortgage companies usually charge interest semi-annually. What would be the effective rate of interest on a mortgage at 8.15 percent compounded semi-annually? O a. 8.23 percent O b. 8.32 percent O c. 8.46 percent O d. 8.40 percent If you want to save $1,000,000 for retirement with $200 monthly deposits (end-of-month) at 6 percent interest compounded monthly, how long will it take? O a. 54.4 years O b. 55.9 years O c. 52.8 years O d. 57.2 years
Answers
a) The effective rate of interest on a mortgage at 8.15 percent compounded semi-annually is 8.23 percent.
b) It will take approximately 54.4 years to save $1,000,000 for retirement with $200 monthly deposits at 6 percent interest compounded monthly.
a) To find the effective rate of interest, we use the formula: Effective Rate = (1 + (Nominal Rate / Number of Compounding Periods))^Number of Compounding Periods - 1.
For a mortgage at 8.15 percent compounded semi-annually, the nominal rate is 8.15 percent and the number of compounding periods is 2 per year.
Plugging these values into the formula, we get Effective Rate = (1 + (0.0815 / 2))^2 - 1 ≈ 0.0823, or 8.23 percent. Therefore, the effective rate of interest on the mortgage is 8.23 percent.
b) To determine how long it will take to save $1,000,000 for retirement with $200 monthly deposits at 6 percent interest compounded monthly, we can use the formula for the future value of an ordinary annuity: FV = P * ((1 + r)^n - 1) / r, where FV is the future value, P is the monthly deposit, r is the monthly interest rate, and n is the number of periods.
Rearranging the formula to solve for n, we have n = log(FV * r / P + 1) / log(1 + r). Plugging in the values $1,000,000 for FV, $200 for P, and 6 percent divided by 12 for r, we get n = log(1,000,000 * (0.06/12) / 200 + 1) / log(1 + (0.06/12)) ≈ 54.4 years.
Therefore, it will take approximately 54.4 years to save $1,000,000 for retirement under these conditions.
Learn more about interest rate here:
https://brainly.com/question/32020793
#SPJ11
Find angle 1
PLS ANSWER ASAP

Answers
Answer:
80 degrees
Step-by-step explanation:
What we see in this drawing is a triangle formed by three lines. In order to solve this problem, we need to know that when two lines intersect, the two angles formed are supplementary (meaning they add up to 180 degrees). For example, the 150-degree angle, and the angle right next to it (the angle on the left side of the triangle) add up to 180 degrees. This means that the left-most angle of the triangle is 180-150, which is 30 degrees
We can figure out the topmost angle of the triangle using the same method. We know that the angle outside the triangle is 130 degrees, so the angle right next to it (in this case, right below it), is 180-130, or 50 degrees.
Next, we use the fact that triangles are 180 degrees on the inside to figure out the third angle (the one on the right, right next to angle 1). We know that the other two angles are 30 and 50 degrees, and if you add that up, you get 80 degrees. The last angle, then, is 180-80, or 100 degrees.
Lastly, we know that the rightmost angle of the triangle and angle 1 add up to 180 degrees. In other words, 100+Angle1=180. Therefore, Angle 1 is 180-100 or 80 degrees.
One gram of protein contains 4 calories. One gram of fat contains 9 calories. A snack has 60 calories from p grams of protein and f grams of fat.
The equation 4p+9f=60 represents the relationship between these quantities.
1. Determine if each pair of values could be the number of grams of protein and fat in the snack. Be prepared to explain your reasoning.
A. 5 grams of protein and 2 grams of fat
B. 10.5 grams of protein and 2 grams of fat
C. 8 grams and 4 grams of fat
2. If there are 6 grams of fat in the snack, how many grams of protein are there? Show your reasoning.
3. In this situation, what does a solution to the equation 4p + 9f = 60 tell us? Give an example of a solution.
Answers
Answer:
Step-by-step explanation:
Equation representing the relationship between the calories from Protein and fat is,
6p + 9f = 60
1). A). If p = 5 grams and f = 2 grams,
Number of calories = (6×5) + (9×2)
= 30 + 18
= 48 calories
B). If p = 10.5 grams and f = 2 grams,
Number of calories = (6×10.5) + (9×2)
= 63 + 18
= 81 calories
C). If p = 8 grams and f = 4 grams
Number of calories = (6×8) + (9×4)
= 48 + 36
= 84 calories
(2). If f = 6 grams, then we have to calculate the grams of protein from the given equation.
4p + (9×6) = 60
4p + 54 = 60
4p = 60 - 54
p = \(\frac{6}{4}=1.5\) grams
(3). Combination of 6 grams of fat and 1.5 grams of protein in a snack gives 60 calories of energy.
In a video game, the player can choose their character. The choices are from 8 animals and 4 humans. Players can also let the game randomly choose
their character
If a player does the random selection, what is the probability that a human character will be chosen?
Enter your answer as a fraction in simplest form in the box
Answers
The probability of selecting a human character randomly in the game is \(\frac{1}{3}\)
The probability that a human character will be chosen when the player selects a character randomly can be calculated by dividing the number of human characters by the total number of available characters.
There are 8 animal characters and 4 human characters, making a total of 12 characters to choose from. Therefore, the probability of selecting a human character randomly is:
P(Human) = Number of human characters / Total number of characters
P(Human) = 4 / 12
Simplifying this fraction, we find:
P(Human) = 1 / 3
Therefore, the probability of selecting a human character randomly is 1/3 or approximately 0.333.
In the given scenario, there are a total of 8 animal characters and 4 human characters, making a total of 12 characters to choose from. When a player selects a character randomly, each character has an equal chance of being chosen. Since there are 4 human characters, the probability of selecting one of them is determined by dividing the number of human characters (4) by the total number of characters (12).
When we simplify the fraction 4/12, we find that it is equal to 1/3.
For more questions on probability
https://brainly.com/question/25839839
#SPJ8
What is 3.68086257145 divided by 6.533 * 4,085,0811
Answers
When 3.68086257145 divided by 6.533 * 4,085,0811 we get 1.379228624370833401829E-8
The methods of division are of three types according to the difficulty level. These are the chunking method or division by repeated subtraction, short division method or bus stop method and long division method.
The division of two numbers can be calculated using the following formula:
Dividend / Divisor = Quotient + Remainder.
The number that is being divided in this case is known as the dividend. The number that divides the number (dividend) into equal parts is known as the divisor.
The quotient is the result of the division operation.
The remainder is the leftover number in the division operation.
We have been given that
3.68086257145 divided by 6.533× 4,085,0811
First we simplify multiplication part
6.533× 4,085,0811 = 266878348.263
Now
3.68086257145 divided by 266878348.263
3.68086257145 ÷ 266878348.263
= 1.379228624370833401829E-8
Hence , 1.379228624370833401829E-8 is the result of the 3.68086257145 divided by 6.533× 4,085,0811 .
To learn more about Division
https://brainly.com/question/24662212
#SPJ1
▸
People attending a basketball game either supported the home team or the visiting
team. If 2940 of the people attending supported the home team and 560 supported
the visiting team, what percentage supported the home team?
Answers
Answer:
84%
Step-by-step explanation:
2940+560=3,500
\(\frac{2940*100}{3500} =\)\(\frac{84}{100}\)
=84%
the table below lists probabilities for the corresponding number of girls in three live births. what is the random variable, what are its possible values, and are its values all numerical?
Answers
The random variable in given problem is "x" . The possible values of random variable x are 0,1,2 and 3..
All possible values of random variable is numrical in nature.
We have a table to right lists probabilities for the corresponding number of girls in three live births.
from the table we cleary see that the random variable is x which represents the number of girls in three live births.
Random variable is a variable whose value is unknown or a variable which assigns a numerical value to each trials in Sample Space.
Also, we can see in list that the number of girls in three live birth values are 0, 1 ,2 and 3 ( 3 live birth)
So, the possible values of random variable x is 4 i.e., 0, 1, 2 and 3..
From data we get a result that all possible values of random variable and it's probabilities are numrical in nature.
To learn more about Random varible ,refer :
https://brainly.com/question/14356285
#SPJ4
am i right or wrong? i think im right but im not sure please help will give brainliest. if im wrong please explain the right answer to me

Answers
Answer:
Correct, good job!
Step-by-step explanation:
45% of $450:
$450 × 0.45 = $202.50
Add the 45% of $450 to $450
$202.50 + $450 = $652.50
I used a different method to double check your work
Procter and Gamble (PG) paid an annual dividend of $2.95 in 2018. You expect PG to increase its dividends by 7.4% per year for the next five years (through 2023), and thereafter by 2.6% per year. If the appropriate equity cost of capital for Procter and Gamble is 8.6% per year, use the dividend-discount model to estimate its value per share at the end of 2018.
Answers
The dividend in 2018 was $2.95, and it is expected to grow at a rate of 7.4% for the next five years and 2.6% thereafter. With an equity cost of capital of 8.6%, the value per share at the end of 2018 can be calculated.
To calculate the value per share at the end of 2018, we need to discount the expected future dividends using the dividend-discount model. The model assumes that the value of a stock is equal to the present value of all its expected future dividends.
First, we need to calculate the dividends for each year from 2019 to 2023. We start with the dividend in 2018, which was $2.95. We then increase it by 7.4% each year for the next five years:
Dividend in 2019 = $2.95 * (1 + 7.4%) = $3.17
Dividend in 2020 = $3.17 * (1 + 7.4%) = $3.40
Dividend in 2021 = $3.40 * (1 + 7.4%) = $3.65
Dividend in 2022 = $3.65 * (1 + 7.4%) = $3.92
Dividend in 2023 = $3.92 * (1 + 7.4%) = $4.22
After 2023, the dividend is expected to grow at a rate of 2.6% per year. To find the value per share at the end of 2018, we discount the future dividends to their present value using the equity cost of capital of 8.6%.
The present value of the dividends can be calculated as follows:
PV = (D1 / (1 + r)) + (D2 / (1 + r)^2) + ... + (Dn / (1 + r)^n)
where PV is the present value, D1 to Dn are the dividends for each year, r is the equity cost of capital, and n is the number of years.
In this case, n = 5 because we are discounting the dividends for the next five years. Let's calculate the present value:
PV = ($3.17 / (1 + 8.6%)) + ($3.40 / (1 + 8.6%)^2) + ($3.65 / (1 + 8.6%)^3) + ($3.92 / (1 + 8.6%)^4) + ($4.22 / (1 + 8.6%)^5)
PV = $3.17 / 1.086 + $3.40 / 1.086^2 + $3.65 / 1.086^3 + $3.92 / 1.086^4 + $4.22 / 1.086^5
PV ≈ $2.91 + $3.07 + $3.24 + $3.41 + $3.59
PV ≈ $16.22
Therefore, the estimated value per share of Procter and Gamble at the end of 2018 using the dividend-discount model is approximately $16.22.
Learn more about cost here: brainly.com/question/14566816
#SPJ11
The dividend in 2018 was $2.95, and it is expected to grow at a rate of 7.4% for the next five years and 2.6% thereafter. With an equity cost of capital of 8.6%, the value per share at the end of 2018 can be calculated.
To calculate the value per share at the end of 2018, we need to discount the expected future dividends using the dividend-discount model.
The model assumes that the value of a stock is equal to the present value of all its expected future dividends. First, we need to calculate the dividends for each year from 2019 to 2023. We start with the dividend in 2018, which was $2.95. We then increase it by 7.4% each year for the next five years:
Dividend in 2019 = $2.95 * (1 + 7.4%) = $3.17
Dividend in 2020 = $3.17 * (1 + 7.4%) = $3.40
Dividend in 2021 = $3.40 * (1 + 7.4%) = $3.65
Dividend in 2022 = $3.65 * (1 + 7.4%) = $3.92
Dividend in 2023 = $3.92 * (1 + 7.4%) = $4.22
After 2023, the dividend is expected to grow at a rate of 2.6% per year. To find the value per share at the end of 2018, we discount the future dividends to their present value using the equity cost of capital of 8.6%.
The present value of the dividends can be calculated as follows:
PV = (D1 / (1 + r)) + (D2 / (1 + r)^2) + ... + (Dn / (1 + r)^n) where PV is the present value, D1 to Dn are the dividends for each year, r is the equity cost of capital, and n is the number of years.
In this case, n = 5 because we are discounting the dividends for the next five years. Let's calculate the present value: PV = ($3.17 / (1 + 8.6%)) + ($3.40 / (1 + 8.6%)^2) + ($3.65 / (1 + 8.6%)^3) + ($3.92 / (1 + 8.6%)^4) + ($4.22 / (1 + 8.6%)^5)
PV = $3.17 / 1.086 + $3.40 / 1.086^2 + $3.65 / 1.086^3 + $3.92 / 1.086^4 + $4.22 / 1.086^5
PV ≈ $2.91 + $3.07 + $3.24 + $3.41 + $3.59
PV ≈ $16.22
Therefore, the estimated value per share of Procter and Gamble at the end of 2018 using the dividend-discount model is approximately $16.22.
Learn more about cost here: brainly.com/question/14566816
#SPJ11
PLEASE HELP!Find the slope of the line on the graph.
Write your answer as a fraction or a whole
number, not a mixed number or decimal
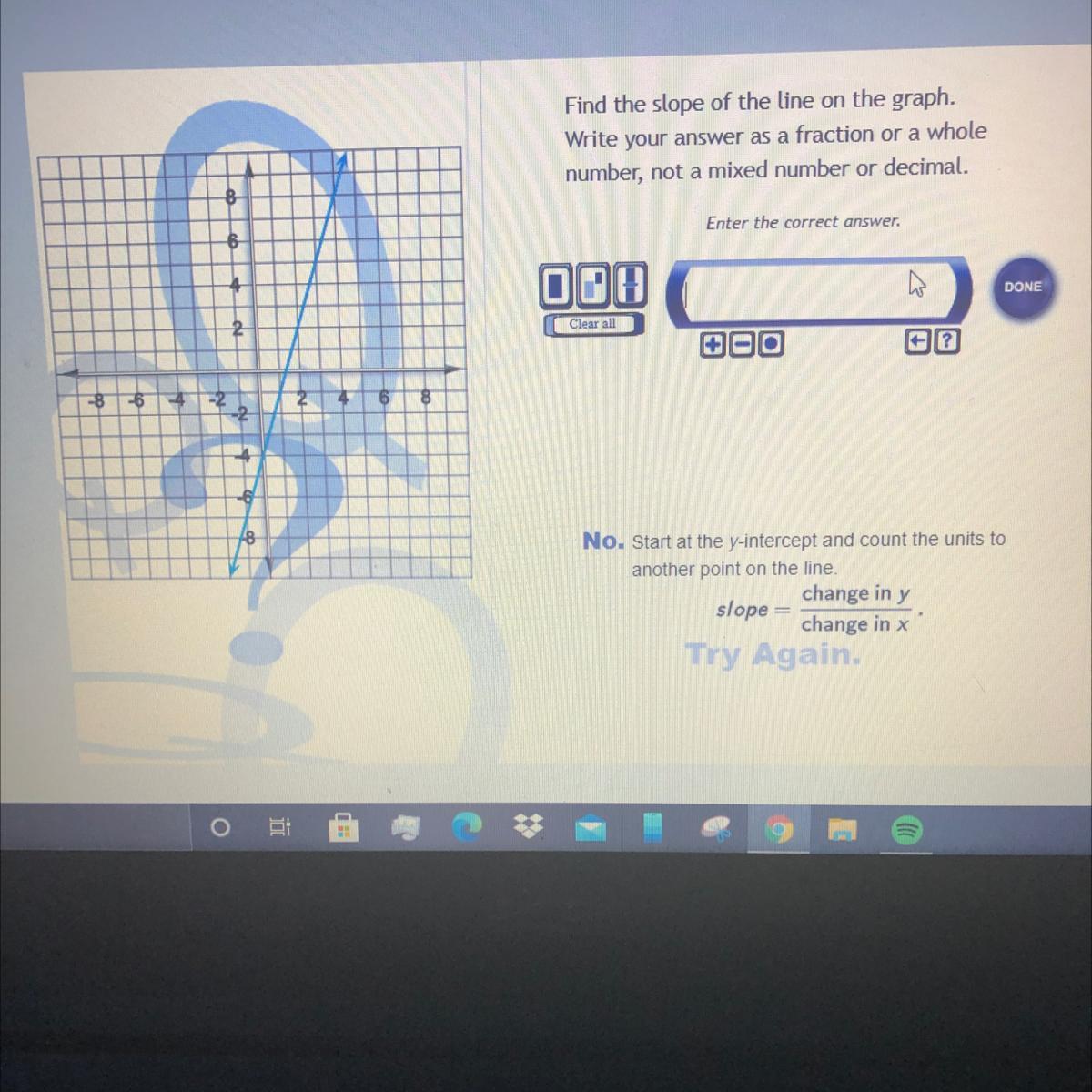
Answers
Answer:
3/1 or 3
Step-by-step explanation:
It rises up three and to the side one
Answer: The slope is 3.
You are considering purchasing a consol that promises annual payments of $4. a. If the current interest rate is 3 percent, what is the price of the consol? Instructions: Round your answer to the nearest penny (2 decimal places). The price of the consol is $ b. You are concerned that the interest rate may rise to 4 percent. Compute the percentage change in the price of the consol and the percentage change in the interest rate. Compare them. Instructions: Round your answer for dollar amounts to the nearest penny (2 decimal places ) and answers for percentages to the nearest tenth (1 decimal place) The new price of the consol would be $ The price of the consol falls by 7% and the interest rises by 7% c. Your investment horizon is one year. You purchase the consol when the interest rate is 5 percent and sell it a year later, following a rise in the interest rate to 6 percent. What is your holding period return? Instructions: Round your answer to the nearest tenth (1 decimal place) Your holding period return is %
Answers
a. The price of the consol is approximately $133.33.
b. The new price of the consol would be $100. The price of the consol falls by 24.99% and the interest rate rises by 1%.
c. Your holding period return is approximately -49.99%.
a. The price of the consol can be calculated using the formula for the present value of a perpetuity:
Price = Annual Payment / Interest Rate
In this case, the annual payment is $4 and the interest rate is 3%. Substituting these values into the formula:
Price = $4 / 0.03 ≈ $133.33
Therefore, the price of the consol is approximately $133.33.
b. To calculate the new price of the consol if the interest rate rises to 4%, we use the same formula:
New Price = Annual Payment / New Interest Rate
Substituting the values, we get:
New Price = $4 / 0.04 = $100
The percentage change in the price of the consol can be calculated using the formula:
Percentage Change = (New Price - Old Price) / Old Price * 100
Substituting the values, we have:
Percentage Change in Price = ($100 - $133.33) / $133.33 * 100 ≈ -24.99%
The percentage change in the interest rate is simply the difference between the old and new interest rates:
Percentage Change in Interest Rate = (4% - 3%) = 1%
Comparing the two percentages, we can see that the price of the consol falls by approximately 24.99%, while the interest rate rises by 1%.
c. The holding period return can be calculated using the formula:
Holding Period Return = (Ending Value - Initial Value) / Initial Value * 100
The initial value is the purchase price of the consol, which is $133.33, and the ending value is the price of the consol after one year with an interest rate of 6%. Using the formula for the present value of a perpetuity, we can calculate the ending value:
Ending Value = Annual Payment / Interest Rate = $4 / 0.06 = $66.67
Substituting the values into the holding period return formula:
Holding Period Return = ($66.67 - $133.33) / $133.33 * 100 ≈ -49.99%
Therefore, the holding period return is approximately -49.99%.
Learn more about holding period
brainly.com/question/32568151
#SPJ11
Escribe una situacion quese represeten con los 60 -4 0 -10 cual es el resultado
Answers
Answer:
Sorry I didn't knowa hypothesis test produces a p-value of 1.5%. which of the following are definitely true? check all answers that apply. group of answer choices a hypothesis test with a significance level of 1.5% can reject the null when it is actually true in 1.5% of the times. the test is statistically significant. the null hypothesis is false. we have observed something unusual if the null hypothesis is true. the alternative hypothesis is true.
Answers
The correct answers are: The test is statistically significant. We have observed something unusual if the null hypothesis is true. The other statements are not necessarily true on the given p-value of 1.5%.
Based on the information provided, we can determine the following:
The test is statistically significant: A p-value of 1.5% indicates that the observed result is unlikely to have occurred by chance, given the null hypothesis.
We have observed something unusual if the null hypothesis is true: A small p-value suggests that the observed data is unlikely to be a result of random chance, which implies that the data is unusual if the null hypothesis is true.
The null hypothesis is not necessarily false: The p-value alone does not provide direct information about the truth or falsehood of the null hypothesis. It only indicates the level of evidence against the null hypothesis.
The alternative hypothesis is not necessarily true: Similarly, the p-value does not provide evidence for the alternative hypothesis being true. It only indicates the strength of evidence against the null hypothesis.
Learn more about p-value here:
https://brainly.com/question/30461126
#SPJ11
In a class of students, the following data table summarizes how many students play
an instrument or a sport. What is the probability that a student chosen randomly
from the class plays a sport?
Plays a sport
Does not play a sport
Plays an instrument Does not play an instrument
3
8
10
9
Answers
Answer:
3 OR 8 hope this helps!
Step-by-step explanation:
how do u do thissss??
reflect this shape in the line y=x :)

Answers
Answer:
the x-coordinate and y-coordinate change places.
Step-by-step explanation: so you reflect a point across the line y = x, the x-coordinate and y-coordinate change places. If you reflect over the line y = -x, the x-coordinate and y-coordinate change places and are negated (the signs are changed). the line y = x is the point (y, x). the line y = -x is the point (-y, -x).