help plsss, i need it asap!!!!! thankss
Answers
Related Questions
Suppose that for a typical FedEx package delivery, the cost of the shipment is a function of the weight of the package measured in ounces. You want to try to predict the cost of a typical shipment given package dimensions. If 10 packages in a city are sampled and the regression output is given below, what can we conclude about the slope of weight
Answers
Answer:
The answer is "Option 5"
Step-by-step explanation:
Please find the complete question in the attached file.
Throughout the above output the regression equation is:
Delivery cost \(=0.469\times weight +9.617\)

A cone has a base area of 24 square inches and a height of 8 inches. What is the area of a cross-section of the cone that is parallel to the base and 3 inches from the vertex?
A circular cross section is marked near the vertex of a cone, parallel to the base.
The area of the cross-section of the cone that is parallel to the base and 3 inches from the vertex is square inches.
Answers
The area of the cross-section of the cone that is parallel to the base and 3 inches from the vertex is 27/8 square inches or 3 3/8 square inches
Calculating the area of the cross section of a coneFrom the question, we are to determine the area of the cross-section of the cone
To determine the area of the cross-section of the cone, we will determine the radius of the cross-section.
Let the radius of the cross-section be x and radius of the base of the be r.
The height of the cone is 8 inches and the height of the cone formed from the cross-section is 3 inches
By similar triangle theorem, we can write that
8/r = 3/x
x = (3r)/8
From the given information,
The area of the base is 24 square inches
Thus,
πr² = 24
Therefore, r² = 24/π
The area of the cross-section will be
A = πx²
But, x = (3r)/8
Thus,
A = π [(3r)/8]²
A = π × 3²/8² × r²
A = π × 9/64 × 24/π
A = 27/8 square inches
Hence, the area is 27/8 square inches or 3 3/8 square inches
Learn more on Calculating area of the cross section of a cone here: https://brainly.com/question/13644548
#SPJ1
highest common factor of 12, 16 wnd 48
Answers
Highest Common factor of 12, 16 and 48 is 4
Answer:
highest common factor of 12, 16 and 48 is 4.
2500 dollars is placed in an account with an annual interest rate of 9%. To the nearest year, how long will it take for the account value to reach 7500 dollars?
Answers
It will take 22 years for the account value to reach $7500 with an annual interest rate of 9% per year.
According to the question,
We have the following information:
2500 dollars is placed in an account with an annual interest rate of 9%.
We know that following formula is used to find simple interest:
Simple interest = principal*rate*time/100
Now, the simple interest on any amount will be equal to the total amount after interest minus the principal amount:
7500-2500
5000
So, we have the following expression:
(2500*9*t)/100 = 5000
Now, using cross multiplication method:
t = (5000*100)/(2500*9)
t = 200/9 years
t = 22.2 years
Now, the nearest year will be 22 years.
Hence, it will take 22 years for the account value to reach $7500 with an annual interest rate of 9% per year.
To know more about interest rate here
https://brainly.com/question/11566183
#SPJ1
( P + 5 ) - 4 = 6
What is the value of P?
Answers
Answer:
ight first you add 4 to 6 and that gets you 10 so you left with p+5=10 then you subtract 5 from 10 so p is gonna be 5
Step-by-step explanation:
True or false? Please help.

Answers
Answer:
True
Step-by-step explanation:
Vertical angles are angles that essentially opposite of eachother. Vertical angles are a pair of opposite angles formed by intersecting lines.
Answer:
True
Step-by-step explanation:
Vertical angles are angles that essentially opposite of eachother. Vertical angles are a pair of opposite angles formed by intersecting lines.
Which graph displays points that correspond to the x and y values in the table?

Answers
hm this is weird, i thought i answered the question. or maybe they're two different questions? line graph because i said so. i know im so helpful
Your friend has a bag of yellow and purple candy. He wants to use them to play a game with you.
Purple is worth 2 points and yellow is worth three points. Pick 9 candies from the bag
Create a system of equations where the combination of the candies gives you a total of 22 points. Make sure you label and define your variables.
Answers
The system of equations where the combination of the candies gives you a total of 22 points are:
x + y = 9
2x + 3y = 22
How can we create system of equations?To create the equations, we shall first define the variables:
x = the number of purple candies
y = the number of yellow candies
Next, we shall use the given information that purple candies are worth 2 points and yellow candies are worth 3 points.
Then, we would make sure that the total number of candies selected is 9.
The first equation represents the total number of candies selected:
x + y = 9
The second equation represents the total number of points obtained:
2x + 3y = 22
Therefore, the system of equations is:
x + y = 9
2x + 3y = 22
This is a system of linear equations.
Learn more about system of linear equations at brainly.com/question/13729904
#SPJ1
three sides of triangle is x cm y cm z cm its perimeter and semi perimeter
Answers
Answer:
Step-by-step explanation:
Perimeter:
\(P=(x+y+z) \ cm\)
Semi-perimeter:
\(SP=\frac{1}{2} (x+y+z) \ cm\)
day!
Altea is making pumpkin spice cupcakes.
She needs 15 ounces of pureed pumpkin
for each batch. If she makes 16 batches of
the cupcakes, how many ounces of the
pureed pumpkin will she need?
o
Answers
Answer:
240oz.
Step-by-step explanation:
15oz=1batch
She needs 16 batches.
15oz. x 16batches = 240oz.
Hope this helps :)
The other dud explained it
Whirly Corporation’s contribution format income statement for the most recent month is shown below:
Total Per Unit
Sales (8,700 units) $ 287,100 $ 33.00
Variable expenses 165,300 19.00
Contribution margin 121,800 $ 14.00
Fixed expenses 55,600
Net operating income $ 66,200
Required:
(Consider each case independently):
1. What would be the revised net operating income per month if the sales volume increases by 40 units?
2. What would be the revised net operating income per month if the sales volume decreases by 40 units?
3. What would be the revised net operating income per month if the sales volume is 7,700 units?
Last month when Holiday Creations, Incorporated, sold 37,000 units, total sales were $148,000, total variable expenses were $115,440, and fixed expenses were $35,800.
Required:
1. What is the company’s contribution margin (CM) ratio?
2. What is the estimated change in the company’s net operating income if it can increase sales volume by 500 units and total sales by $2,000? (Do not round intermediate calculations.)
Answers
1. Revised Net Operating Income = $66,760
2. Revised Net Operating Income =$64,640
3. Revised Net Operating Income =$52,
1. If the sales volume increases by 40 units:
So, New Sales = 8,700 units + 40 units = 8,740 units
and, New Contribution Margin =
= $14.00 x 8,740 units
= 122, 360
New Fixed Expenses remain the same at $55,600
Then, Revised Net Operating Income
= New Contribution Margin - New Fixed Expenses
= 122360 - 55600
= 66,760.
2. If the sales volume decreases by 40 units:
New Sales = 8,700 units - 40 units = 8,660 units
New Contribution Margin
= 14 x 8660
= 121,240
New Fixed Expenses remain the same at $55,600
Then, Revised Net Operating Income
= New Contribution Margin - New Fixed Expenses
= 65,640
3. If the sales volume is 7,700 units:
New Sales = 7,700 units
New Contribution Margin
= 14 x 7700
= 107,800
New Fixed Expenses remain the same at $55,600
Then, Revised Net Operating Income
= New Contribution Margin - New Fixed Expenses
= 52, 200
Learn more about Income Format here:
https://brainly.com/question/15312142
#SPJ1
Ophthalmology students compared two types of detached retina surgery to determine if patients were able to regain vision. They studied laser surgery and freezing treatment. Identify the response and explanatory variables.
Answers
Answer:
- Response variable: The amount of vision the patients obtained after surgery.
- Explanatory variable: The type of detached retina surgery carried out.
Step-by-step explanation:
Response variable is the main focus of a question when carrying out a study or experiment. Whereas, an explanatory variable is the variable one that explains the changes in the response variable.
Now, in the question we are given it is clear that the main focus of the study is to determine if patients were able to regain vision.
Thus, the response variable is; the amount of vision the patients obtained after surgery.
Now, what determines if patients were able to regain vision is hinged on the 2 retina surgeries which are: laser surgery and freezing treatment.
Thus, the explanatory variable is; The type of detached retina surgery.
Please help me 15 points

Answers
Answer:
1 Solution
Step-by-step explanation:
Write an equation in slope-intercept form (-5,-7);y=-2x+4
Answers
Answer:
Step-by-step explanation:
First, let us substitute x and y values: -7 = -2(-5) + 4
Next, let us simplify using the substitution property of equality: 14 = -7 (SEE BELOW MORE INFO).
Now, this does not make sense yet because 14 cannot possibly equal -7. Therefore, we must add a b value, therefore leading us to the equation:
14 + b = -7
by simplifying, we can conclude that b = -21
Finally, we can plug in the b-value into our original equation:
y = -2x + 4 - 21
After simplifying, we get y = -2x - 17. When this is graphed, we can see that -2x - 17 intersects (-5, -7).
What is the meaning of "the notion of finiteness"?

Answers
The notion of finiteness refers to the idea that something has a definite limit or is not infinite. It is a concept that has been applied in various fields of study, such as mathematics, computer science, and philosophy.
In mathematics, finiteness is a fundamental concept used to define various mathematical objects and structures, such as sets, numbers, and sequences. It is also used to define the properties of functions and to study the properties of mathematical systems.
In computer science, the notion of finiteness is crucial for the design and analysis of algorithms and computer programs. Computer scientists use finite state machines, which are mathematical models that describe the behavior of a system that can be in one of a finite number of states.
This concept is essential to the development of computer programs that are efficient, reliable, and secure.
In philosophy, finiteness is a concept that is often used to reflect on the nature of human existence and the limits of human knowledge. It is also used to examine the concept of time and the nature of reality.
In general, the notion of finiteness is a fundamental concept that has many applications in various fields of study.
To learn more about : finiteness
https://brainly.com/question/32403180
#SPJ8
anyone? giving brainliest to correct answer
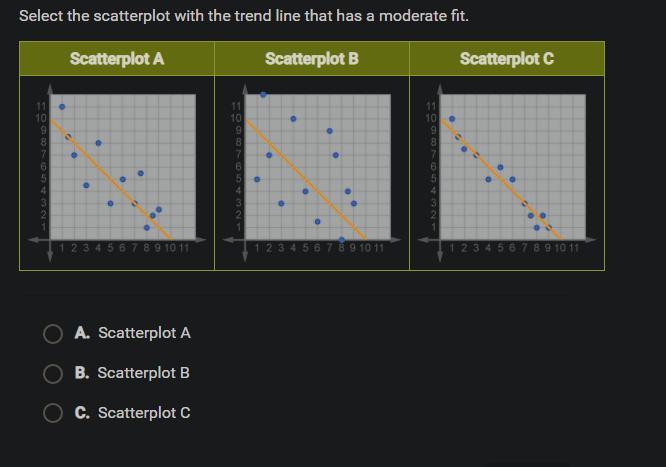
Answers
Answer:
im not really sure what that means im so sorry
Step-by-step explanation:
Pls help me with this 500 points for this

Answers
Answer:
2,2,4,5,7
Mode = most numbers in the group, has to be more than one of it (2)
Range = subtract the lowest number from the highest number \(7-2=5\)
Median = the number in the middle (4)
Mean = add all the numbers together and divide by the quantity in a set
\(\frac{2+2+4+5+7}{5} =4\)
What is the equation of the line that is parallel to the line defined by the equation y = 3x−7 and goes through the point (4, 2)?
Answers
Answer:
\(y-2=3(x-4)\)
Step-by-step explanation:
Pre-SolvingWe are given a line contains the point (4, 2).
We also know that the line is parallel to y= 3x - 7.
We want to write the equation of this line.
Parallel lines have the same slopes.
First, let's find the slope of y = 3x - 7.
3 is in the place of where m (the slope) is, so that means it is the slope of that line.
It is also the slope of the line whose equation we want to write.
The equation of the line can be written in three ways:
Slope-intercept form, which is y=mx+b, where m is the slope and b is the y-intercept. Standard form, which is ax+by=c, where a, b, and c are free integer coefficients. a and b cannot be 0, and a is usually non-negative as well. Point-slope form, which is \(y-y_1=m(x-x_1)\), where m is the slope and \((x_1, y_1)\) is a point.All of these ways are valid, but for this problem, let's write the equation in point-slope form, as it is the easiest.
SolvingSubstitute 3 as m in \(y-y_1=m(x-x_1)\).
\(y-y_1=3(x-x_1)\)
Now, substitute 4 as \(x_1\) and 2 as \(y_1\).
\(y-2=3(x-4)\)
Topic: parallel and perpendicular lines
See more: https://brainly.com/question/7699889
The first triangle is dilated to form the second triangle Select True or Flause

Answers
Answer:
Statement 1 is false, statement 2 is true.
Step-by-step explanation:
The triangle has been dialated by a scale factor of 2.5
What is the diference between the
largest and the smallest 4 digit numbers
Answers
largest 4 digit number : 9999
smallest 4 digit numbers : 1000
Difference = 9999 - 1000 = 8999
What will be the new coordinate of vertex B if the triangle is dilated with a center at the origin by a scale factor of 1/3
Answers
You must observe the distances from the center of the dilation at point A to the other points B, C and D. The dilation image will be 1/3 of each of these distances. AB = 6, so A'B' = 2. AD = 9, so A'D' = 3.
Can I get brainllest
Your given two side lengths of 3 centimeters and 5 centimeters
Answers
Answer:
Can it be any length? If so, 4 centimeters would work, since it could make a 3-4-5 right triangle.
Step-by-step explanation:
that what i got
How many solutions does the system of equations below have? y=-3/4x+1/6
Answers
The solution is the point (0, 1/6) y = 1/6
Given the equation y = (-3/4)x + 1/6, which represents a linear equation, there is no "system" of equations involved since there is only one equation.
In this case, the equation is in slope-intercept form (y = mx + b),
where m represents the slope (-3/4) and b represents the y-intercept (1/6).
The slope-intercept form allows us to determine various properties of the equation.
Since there is only one equation, the solution to this equation is a single point on the Cartesian plane.
Each pair of x and y values that satisfy the equation represents a solution.
For example, if we choose x = 0, we can substitute it into the equation to find the corresponding y value:
y = (-3/4)(0) + 1/6
y = 1/6
Therefore, the solution is the point (0, 1/6).
In summary, the given equation has a unique solution, represented by a single point on the Cartesian plane.
Any value of x plugged into the equation will yield a corresponding y value, resulting in a unique point that satisfies the equation.
For similar question on linear equations.
https://brainly.com/question/22688504
#SPJ8
(q1) Find the length of the curve described by the function

Answers
The value of the Integral at the lower limit from the value of the integral at the upper limit to get the length of the curve.
The length of the curve described by the function f(x) = 1 + 3x^2 + 2x^3 is to be found. The formula used to find the length of a curve is:
L = ∫(sqrt(1 + [f'(x)]^2))dx where f'(x) is the derivative of f(x)We have to first find f'(x):f(x) = 1 + 3x^2 + 2x^3f'(x) = 6x + 6x^2
The integral becomes:L = ∫(sqrt(1 + [6x + 6x^2]^2))dx = ∫(sqrt(1 + 36x^2 + 72x^3 + 36x^4))dx The integral appears to be difficult to evaluate by hand.
Therefore, we use software like Mathematica or Wolfram Alpha to solve the problem. Integrating the expression using Wolfram Alpha gives:
L = 1/54(9sqrt(10)arcsinh(3xsqrt(2/5)) + 2sqrt(5)(2x^2 + 3x)sqrt(9x^2 + 4))The limits of integration are not given. Therefore, the definite integral be solved.
We can, however, find a general solution. We use the above formula and substitute the limits of integration.
Then, we subtract the value of the integral at the lower limit from the value of the integral at the upper limit to get the length of the curve.
To know more about Integral.
https://brainly.com/question/27419605
#SPJ8
What is the answer to log↓2(x)-3=1
Answers
If IK=JK, find mlJ
A. 72°
B. 82°
C. 122°
D. 134°
Answers
Answer:
D.134
Step-by-step explanation:
What's the first term of the expansion of (x+y)9?
Answers
Y (4)
+4y ′′
+4y=0 A general solution with x as the independent variable is y(x)=
Answers
Answer:
Step-by-step explanation:
We can use the method of undetermined coefficients to solve this differential equation. First, we will need to find the solution to the homogeneous equation and the particular solution to the non-homogeneous equation.
For the homogeneous equation, we will use the form y"+ky=0, where k is a constant. We can find the solutions to this equation by letting y=e^mx,
y"=m^2e^mx -> (m^2)e^mx+k*e^mx=0, therefore (m^2+k)e^mx=0
(m^2+k) should equal 0 for the equation to have a non-trivial solution. Therefore, m=±i√(k), and the general solution to the homogenous equation is y=A*e^i√(k)x+Be^-i√(k)*x.
Now, we need to find the particular solution to the non-homogeneous equation. We can use the method of undetermined coefficients to find the particular solution. We will let yp=a0+a1x+a2x^2+.... As the derivative of a sum of functions is the sum of the derivatives, we get
yp″=a1+2a2x....yp‴=2a2+3a3x+....
Substituting the general solution into the non-homogeneous equation, we get
a0+a1x+a2x^2+...+2a2x+3a3x^2+...=Y(4)
So, the coefficient of each term in the expansion of the left hand side should equal the coefficient of each term in the expansion of the right hand side. Since there is only one term on the right hand side, we get the recurrence relation:
a(n+1)=Y(n-2)/n^2
From this relation, we can find all the coefficients in the expansion for the particular solution. Using this particular solution, we can find the total solution to the differential equation as the sum of the homogeneous solution and the particular solution.
75° b Arrange the three side lengths in increasing order. 350 c [?]
![75 b Arrange the three side lengths in increasing order. 350 c [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/yGS8eIStBed2VXKQT4g6eEWdYvZD4F36.jpeg)
Answers
Answer:
a < b < c
Step-by-step explanation:
The side opposite the larger angle measure is the longer side.
The side opposite the smallest angle measure is the shortest side.
The sum of the three angles = 180° ; (75° + 35° + ? = 180°). The missing angle is 70°
The angles in order from the smallest to the largest:
35° < 70° < 75°
The side for the shortest to the largest
side opposite 35° is a
side opposite 70° is b
side opposite 75° is c
Answer a < b < c
Using angle sum property in △ABC
∠A+∠B+∠C=180
∘
⇒50
∘
+60
∘
+∠C=180
∘
⇒∠C=70
∘
In any triangle side opposite to the largest angle is the longest side.
Here ∠C is largest and side opposite to it is AB
∴AB is the longest side.
Then comes ∠B and side opposite to it is AC
∴AC is the second longest side.
Then comes ∠A and side opposite to it is AC
∴BC is the shortest side.
So the increasing order of sides is
BC
NO LINKS!! URGENT HELP PLEASE!!
1. Find the area of a regular octagon. Each side is 12 m.
2. The perimeter of a regular polygon is 72 feet. An exterior angle of the polygon measures 40°. Find the length of each side.
3. If the perimeter of a regular pentagon is 50 in. Find the area. Show a drawing and work please.
Answers
Answer:
1) 695.3 m²
2) 8 ft
3) 172.0 in²
Step-by-step explanation:
Question 1To find the area of a regular polygon, we can use the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
Given the polygon is an octagon, n = 8.
Given each side measures 12 m, s = 12.
Substitute the values of n and s into the formula for area and solve for A:
\(\implies A=\dfrac{(12)^2 \cdot 8}{4 \tan\left(\dfrac{180^{\circ}}{8}\right)}\)
\(\implies A=\dfrac{144 \cdot 8}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{1152}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{288}{\tan\left(22.5^{\circ}\right)}\)
\(\implies A=695.29350...\)
Therefore, the area of a regular octagon with side length 12 m is 695.3 m² rounded to the nearest tenth.
\(\hrulefill\)
Question 2The sum of an interior angle of a regular polygon and its corresponding exterior angle is always 180°.
If the exterior angle of a polygon measures 40°, then its interior angle measures 140°.
To determine the number of sides of the regular polygon given its interior angle, we can use this formula, where n is the number of sides:
\(\boxed{\textsf{Interior angle of a regular polygon} = \dfrac{180^{\circ}(n-2)}{n}}\)
Therefore:
\(\implies 140^{\circ}=\dfrac{180^{\circ}(n-2)}{n}\)
\(\implies 140^{\circ}n=180^{\circ}n - 360^{\circ}\)
\(\implies 40^{\circ}n=360^{\circ}\)
\(\implies n=\dfrac{360^{\circ}}{40^{\circ}}\)
\(\implies n=9\)
Therefore, the regular polygon has 9 sides.
To determine the length of each side, divide the given perimeter by the number of sides:
\(\implies \sf Side\;length=\dfrac{Perimeter}{\textsf{$n$}}\)
\(\implies \sf Side \;length=\dfrac{72}{9}\)
\(\implies \sf Side \;length=8\;ft\)
Therefore, the length of each side of the regular polygon is 8 ft.
\(\hrulefill\)
Question 3The area of a regular polygon can be calculated using the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
A regular pentagon has 5 sides, so n = 5.
If its perimeter is 50 inches, then the length of one side is 10 inches, so s = 10.
Substitute the values of s and n into the formula and solve for A:
\(\implies A=\dfrac{(10)^2 \cdot 5}{4 \tan\left(\dfrac{180^{\circ}}{5}\right)}\)
\(\implies A=\dfrac{100 \cdot 5}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{500}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{125}{\tan\left(36^{\circ}\right)}\)
\(\implies A=172.047740...\)
Therefore, the area of a regular pentagon with perimeter 50 inches is 172.0 in² rounded to the nearest tenth.
Answer:
1.695.29 m^2
2.8 feet
3. 172.0477 in^2
Step-by-step explanation:
1. The area of a regular octagon can be found using the formula:
\(\boxed{\bold{Area = 2a^2(1 + \sqrt{2})}}\)
where a is the length of one side of the octagon.
In this case, a = 12 m, so the area is:
\(\bold{Area = 2(12 m)^2(1 + \sqrt{2}) = 288m^2(1 + \sqrt2)=695.29 m^2}\)
Therefore, the Area of a regular octagon is 695.29 m^2
2.
The formula for the exterior angle of a regular polygon is:
\(\boxed{\bold{Exterior \:angle = \frac{360^o}{n}}}\)
where n is the number of sides in the polygon.
In this case, the exterior angle is 40°, so we can set up the following equation:
\(\bold{40^o=\frac{ 360^0 }{n}}\)
\(n=\frac{360}{40}=9\)
Therefore, the polygon has n=9 sides.
Perimeter=72ft.
We have
\(\boxed{\bold{Perimeter = n*s}}\)
where n is the number of sides in the polygon and s is the length of one side.
Substituting Value.
72 feet = 9*s
\(\bold{s =\frac{ 72 \:feet }{ 9}}\)
s = 8 feet
Therefore, the length of each side of the polygon is 8 feet.
3.
Solution:
A regular pentagon has five sides of equal length. If the perimeter of the pentagon is 50 in, then each side has a length = \(\bold{\frac{perimeter}{n}=\frac{50}{5 }= 10 in.}\)
The area of a regular pentagon can be found using the following formula:
\(\boxed{\bold{Area = \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *s^2}}\)
where s is the length of one side of the Pentagon.
In this case, s = 10 in, so the area is:
\(\bold{Area= \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *10^2=172.0477 in^2}\)
Drawing: Attachment
