Answers
Related Questions
Given: Circle C; Angle LRC is congruent to Angle EIC
Prove: Triangle LRC is congruent to Triangle EIC

Answers
Answer:
\({\triangle LRC} \cong {\triangle EIC}\) by angle-angle-side (\(\texttt{AAS}\).)
Step-by-step explanation:
Let \(r\) denote the radius of this circle.
Notice that \(EC\) and \(LC\) are each a radius of this circle. (A radius of a circle is a segment with one end at the center of the circle and the other end on the perimeter of the circle.)
Therefore, the length of both segment \(EC\) and segment \(LC\) should be equal to the radius of this circle:
\(r = \overline{EC}\).
\(r = \overline{LC}\).
Therefore, \(\overline{EC} = \overline{LC}\).
Thus, \({\triangle LRC} \cong {\triangle EIC}\) by angle-angle-side (\(\texttt{AAS}\)) since:
\({\angle RCL} = {\angle ICE}\) (same angle.)\({\angle LRC} \cong {\angle EIC}\) (given.)\(\overline{EC} = \overline{LC}\).What is the mean of the values in the stem-and-leaf plot?
Enter your answer in the box.

Answers
Answer:
mean = 24
Step-by-step explanation:
the mean is calculated as
mean = \(\frac{sum}{count}\)
the sum of the data set is
sum = 12 + 13 + 15 + 28 + 28 + 30 + 42 = 168
there is a count of 7 in the data set , then
mean = \(\frac{168}{7}\) = 24
If np is greater than or equal to 5 and nq is greater than or equal to 5, estimate P (more than 9) with n=12 and p= 0.3 by using the normal distribution as an approximation to the binomial distribution, if np<5 or nq<5, then state that the normal approximation is not suitable
Answers
The normal approximation is not suitable as np<5.
Given,
mean = np
It turns out that if np and nq are both at least 5, the normal distribution can be used to approximate the binomial distribution. Additionally, keep in mind that a binomial distribution has a mean of np and variance of npq.
Hence apply the mean formula and get the value for np
n= 12 and p=0.
therefore mean = np
np = n×p
np = 12×0.3×
np = 3.6
np is less than 5.
nq=?
q=1-p
q=1-0.3
q=0.7
∴nq = 12 × 0.7
nq = 8.4
nq is not less than 5
It's remarkable that the normal distribution may accurately represent the binomial distribition when n, np and nq are large.
since here only nq is greater than five and np is less than five, therefore we conclude that normal approximation is not suitable.
Hence np<5 so normal approximation is not suitable.
Learn more about "normal distribution" here-
brainly.com/question/4079902
#SPJ10
Suppose the life time (in hours) of a battery brand is normally distributed. A random sample of 16 batteries results in a sample variance of
3.25
hours
2
. We want to test if there is significant/sufficient evidence in the sample data to claim that the variance of the battery life population is different than 4 hours
2
at significance level of
0.05
. Which of the following is INCORRECT? A.
H 0
:σ 2
=4 vs H 1
:σ 2
=4
B. The test statistic is found to be
12.1875
C. We should reject the null hypothesis and there is sufficient evidence to claim that the variance of battery life is different than 4 hours
2
at significance level of
0.05
. D. None of the above.
Answers
there is not sufficient evidence to claim that the variance of the battery life population is different than 4 hours2 at a significance level of 0.05.
answer is D. None of the above.
To test if there is significant evidence to claim that the variance of the battery life population is different than 4 hours2, we can use a chi-square test.This is how the test statistic is computed:
X2 = (n-1)*(s2/σ2)
where n is the sample size, s2 is the sample variance and σ2 is the population variance.
In this case, n = 16, s2 = 3.25 and σ2 = 4
X2 = (16-1)*(3.25/4) = 12.1875
The critical value of X2 with 15 degrees of freedom and α = 0.05 is 24.996. Therefore, since 12.1875 < 24.996, we fail to reject the null hypothesis, and there is not sufficient evidence to claim that the variance of the battery life population is different than 4 hours2 at a significance level of 0.05.
Learn more about variance here
https://brainly.com/question/13708253
#SPJ4
Which 2 grids have 25% shaded?
a)
b)
c)
d)

Answers
Answer:
C and B
Step-by-step explanation:
if u observed carefully u will see option c has
5 boxes coverd out of 20
5*100/20
= 25%
AND IF U OBSERVED CARFULLY WILL SEE OPTION B
4 TRIANGLES ARE COVERED AND TOTAL TRIANGLES ARE 16 SO
100*4/16
= 100/4
= 25%.
HOPE ITS HELPFUL
PLS MARK AS BRILLENT
ABOVE ANSWER IS WROUNG
Marc wants to know if the mean age of the prison population in his city is less than 26 years. He obtains a random sample of 25 prisoners, and finds a mean age of 24.4 years and a standard deviation of 9.2 years. Ata significance level of 0.05, what is his conclusion?
Answers
Answer:
gsgsbsbsbs
Step-by-step explanation:
yewhsgshdhhssjbs
A company's mean salary is $65,000 with a standard deviation of $6,000. What is the salary of a person who is at the 30th percentile for company salaries?
Answers
With mean salary=$65000, a person at the 30th percentile for company salaries would have a salary of approximately $61,544.40.
What exactly is mean?
In mathematics, the mean is a measure of central tendency that represents the average of a set of data. It is also known as the arithmetic mean, and it is calculated by adding up all the values in the dataset and dividing the total by the number of values.
For example, consider the following set of numbers: 3, 5, 7, 8, 10. To find the mean, we add up all the numbers and divide by the total number of values in the set:
Mean = (3 + 5 + 7 + 8 + 10) / 5 = 6.6
Now,
To find the salary of a person who is at the 30th percentile for company salaries
Find the z-score corresponding to the 30th percentile. The z-score is the number of standard deviations a value is away from the mean.
z = invNorm(0.30) = -0.5244 (using a standard normal distribution table )
Use the z-score formula to find the corresponding salary:
z = (x - mu) / sigma
where x is the salary we want to find, mu is the mean salary, sigma is the standard deviation
Rearranging the formula, we get:
x = z * sigma + mu
Substituting the values we have, we get:
x = -0.5244 * $6,000 + $65,000
x = $61,544.40
Therefore, a person at the 30th percentile for company salaries would have a salary of approximately $61,544.40.
To know more about Mean visit the link
https://brainly.com/question/30112112
#SPJ1
For the following exercises, consider the function f(x) = (1+x)^1/x. Round all answers to five decimal places. Evaluate f(-0.01).
Answers
The value of f(-0.01) is approximately 0.99005.
To evaluate f(-0.01), we substitute -0.01 into the function f(x) = (1+x)^(1/x). Thus, we have f(-0.01) = (1+(-0.01))^(1/(-0.01)).
Using a calculator, we simplify this expression to f(-0.01) = 0.99005. Therefore, the value of f(-0.01) rounded to five decimal places is approximately 0.99005.
The function f(x) = (1+x)^(1/x) represents an exponential function with a variable exponent. In this case, we are evaluating the function at x = -0.01.
By substituting this value into the function and performing the necessary calculations, we find that f(-0.01) is approximately 0.99005. This means that when x is equal to -0.01, the function value is approximately 0.99005.
For more such answers on function
https://brainly.com/question/11624077
#SPJ8
Anna volunteers on the weekend at the Central Library. As a school project, she decides to record how many people visit the library, and where they go. On Saturday, 382 people went to The Youth Wing, 461 people went to Social Issues, and 355 went to Fiction and Literature. On Sunday, the library had 800 total visitors. Based on what Anna had recorded on Saturday, about how many people should be expected to go to The Youth Wing? Round your answer to the nearest whole number.
Answers
Based on the data recorded by Anna on Saturday, we can estimate the number of people expected to visit The Youth Wing on Sunday.
Let's calculate the proportion of visitors to The Youth Wing compared to the total number of visitors on Saturday:
\(\displaystyle \text{Proportion} = \frac{\text{Visitors to The Youth Wing on Saturday}}{\text{Total visitors on Saturday}} = \frac{382}{382 + 461 + 355}\)
Next, we'll apply this proportion to the total number of visitors on Sunday to estimate the number of people expected to go to The Youth Wing:
\(\displaystyle \text{Expected visitors to The Youth Wing on Sunday} = \text{Proportion} \times \text{Total visitors on Sunday}\)
Now, let's substitute the values into the equation and calculate the estimated number of visitors to The Youth Wing on Sunday:
\(\displaystyle \text{Proportion} = \frac{382}{382 + 461 + 355}\)
\(\displaystyle \text{Expected visitors to The Youth Wing on Sunday} = \text{Proportion} \times 800\)
Calculating the proportion:
\(\displaystyle \text{Proportion} = \frac{382}{382 + 461 + 355} = \frac{382}{1198}\)
Calculating the estimated number of visitors to The Youth Wing on Sunday:
\(\displaystyle \text{Expected visitors to The Youth Wing on Sunday} = \frac{382}{1198} \times 800\)
Simplifying the equation:
\(\displaystyle \text{Expected visitors to The Youth Wing on Sunday} \approx \frac{382 \times 800}{1198}\)
Now, let's calculate the approximate number of visitors to The Youth Wing on Sunday:
\(\displaystyle \text{Expected visitors to The Youth Wing on Sunday} \approx 254\)
Therefore, based on the data recorded on Saturday, we can estimate that around 254 people should be expected to go to The Youth Wing on Sunday.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Select the correct answer.
Simplify the expression.

Answers
Answer:
The answer to the question is C
Please answer, will give 5 star.

Answers
Answer:
The first one
Step-by-step explanation:
She cant buy anything over $15, but she can buy something thats $15 :))
need help asap. 10 points

Answers
Bc of the alternate angle thing I don’t remember what it’s called
Anddd
For B
180-138= 42=42+29=71
180-71=109
Therefore a is 109
32 +20 is 52
180-52 =128
7TH GRADE MATH IF YOU HELP ILL GIVE BRANLIEST AND 10 POINT//PROBABILITY

Answers
Answer:
1. 1 in 5
2. There are 5 colors it could land on, and orange is one of them.
3. 40 different combinations
4. There are 5 colors with 8 corresponding numbers. 5x8=40
Step-by-step explanation:
1) 20%
2) Assuming that on the spinner with color, every section has an equal share, then the probability of landing on orange is \(\frac{1}{5}\) or 20%. This is because, the orange section is one of the five equal sections, or \(\frac{1}{5}\) or the spinner. \(\frac{1}{5}\) in decimal form is 0.2, to convert to a percent, multiply by 100. Hence one gets, 20%.
3) 40
4) There are 5 sections on the spinner with color, hence 5 possible outcomes when one spins the spinner. On the black and white spinner, there are 8 sections, hence 8 possible outcomes when one spins the spinner. To find the total number of outcomes resulting from the two events, one must multiply the total outcomes from one event by the total outcome of the other event. When one does this, they get that there are 40 possible events.
Ivanna is saving money to buy a game. So far she has saved $12, which is 3/4 of the total cost of the game. How much does the game cost?
Answers
Answer:
24?
Step-by-step explanation:
sabihin nyo kung mali -_-
Please help with this question ASAP

Answers
Answer:
B. 28/15
Step-by-step explanation:
7/3 x 4/5 = 28/15
QuestionEvaluate-6c2 + 2cd + 3d - 4when c = 1 and d =6d - 3+2. Enter an integer or a fraction.Provide your answer below:I need help
Answers
ok
[-6c(2) + 2cd + 3d - 4] / [6d - 3] Is this correct?
c = 1 d = 2
Substitution
[-6(1)(2) + 2(1)(2) + 3(2) - 4 ] / 6(2) - 3
[-12 + 4 + 6 - 4] / [12 - 3]
[-6] / [9]
-2/3
I think that was the equation
The solution is a fraction: -2/3
2. Andrew made an error in determining the polynomial equation of smallest degree whose roots are 3, 2+2i and 2-2i.
Review Andrew’s work, identify the error and correct all work from that point forward that is affected by this error. Include at least one sentence explaining his error. Use proper mathematical vocabulary, appropriately.

Answers
The polynomial equation for the given roots is x³-7x²+20x-24=0.
Given that, the polynomial equation of the smallest degree whose roots are 3, 2+2i and 2-2i.
Now, we need to write the polynomial equation.
What is a polynomial equation?A polynomial equation is an equation where a polynomial is set equal to zero. i.e., it is an equation formed with variables, non-negative integer exponents, and coefficients together with operations and an equal sign. It has different exponents. The highest one gives the degree of the equation. For an equation to be a polynomial equation, the variable in it should have only non-negative integer exponents. i.e., the exponents of variables should be only non-negative and they should neither be negative nor be fractions.
Now, x=3, x=2+2i and x=2-2i
x-3, x-2-2i and x-2+2i
So, the polynomial equation is (x-3)(x-2-2i)(x-2+2i)=0
⇒(x-3)(x(x-2-2i)-2(x-2-2i)+2i(x-2-2i))=0
⇒(x-3)(x²-2x-2xi-2x+4+4i+2xi-4i-4i²)=0
⇒(x-3)(x²-2x-2x+4-4i²)=0
⇒(x-3)(x²-4x+4+4)=0 (∵i²=-1)
⇒(x-3)(x²-4x+8)=0
⇒x(x²-4x+8)-3(x²-4x+8)=0
⇒x³-4x²+8x-3x²+12x-24=0
⇒x³-7x²+20x-24=0
Therefore, the polynomial equation for the given roots is x³-7x²+20x-24=0.
To learn more about the polynomial equation visit:
https://brainly.com/question/20630027.
#SPJ1
Functions
Question 22 of 25
True or false: f(x) is a function.
8
12
O A. False
OB. True
SUBMIT
Answers
The amount of time that people spend at Grover Hot Springs is normally distributed with a mean of 68 minutes and a standard deviation of 14 minutes. Suppose one person at the hot springs is randomly chosen. Let X = the amount of time that person spent at Grover Hot Springs . Round all answers to 4 decimal places where possible.
a. What is the distribution of X? X ~ N(
68
Correct,
14
Correct)
b. Find the probability that a randomly selected person at the hot springs stays longer then 81 minutes.
c. The park service is considering offering a discount for the 8% of their patrons who spend the least time at the hot springs. What is the longest amount of time a patron can spend at the hot springs and still receive the discount?
minutes.
d. Find the Inter Quartile Range (IQR) for time spent at the hot springs.
Q1:
minutes
Q3:
minutes
IQR:
minutes
Answers
a. The distribution of X is X ~ N(68, 14).
b. The corresponding area to the right of 0.9286, which is approximately 0.1772.
c. The longest amount of time a patron can spend and still receive the discount is approximately 48.5654 minutes.
d. The Inter Quartile Range (IQR) for time spent at the hot springs is approximately 21.373 minutes.
a. The distribution of X is X ~ N(68, 14), where X represents the amount of time a person spends at Grover Hot Springs, 68 is the mean, and 14 is the standard deviation.
b. To find the probability that a randomly selected person stays longer than 81 minutes, we need to calculate the area under the normal curve to the right of 81.
Using the z-score formula: z = (x - μ) / σ, where x is the value (81), μ is the mean (68), and σ is the standard deviation (14).
Plugging in the values, we have z = (81 - 68) / 14 = 0.9286.
Using a standard normal distribution table or a calculator, we can find the corresponding area to the right of 0.9286, which is approximately 0.1772.
c. To find the longest amount of time a patron can spend at the hot springs and still receive the discount, we need to find the value that corresponds to the lowest 8% of the distribution.
Using a standard normal distribution table or a calculator, we can find the z-score that corresponds to the 8th percentile, which is approximately -1.4051.
Using the z-score formula, we can calculate the longest amount of time: x = μ + z \(\times\) σ = 68 + (-1.4051) \(\times\) 14 = 48.5654 minutes.
Therefore, the longest amount of time a patron can spend and still receive the discount is approximately 48.5654 minutes.
d. The Inter Quartile Range (IQR) is a measure of the spread of the data and represents the range between the first quartile (Q1) and the third quartile (Q3).
To find Q1 and Q3, we can use the z-score formula and the standard normal distribution table.
For Q1, we find the z-score corresponding to the 25th percentile, which is approximately -0.6745.
Using the formula Q1 = μ + z \(\times\) σ, we have Q1 = 68 + (-0.6745) \(\times\) 14 = 57.053.
Therefore, Q1 is approximately 57.053 minutes.
For Q3, we find the z-score corresponding to the 75th percentile, which is approximately 0.6745.
Using the formula Q3 = μ + z \(\times\) σ, we have Q3 = 68 + (0.6745) \(\times\) 14 = 78.426.
Therefore, Q3 is approximately 78.426 minutes.
Finally, we can calculate the IQR by subtracting Q1 from Q3: IQR = Q3 - Q1 = 78.426 - 57.053 = 21.373 minutes.
Therefore, the Inter Quartile Range (IQR) for time spent at the hot springs is approximately 21.373 minutes.
For similar question on distribution.
https://brainly.com/question/24802582
#SPJ8
Which of the following are disadvantages of the mode?
For many sets of data there are multiple modes.
The mode is affected by extremely large and small values.
For many sets of data there is no mode.
the mode can only be computed for interval-level data or higher
Answers
The disadvantages of the mode are: For many sets of data there is no mode.
The mode is a measure of central tendency that represents the most frequently occurring value in a dataset.
However, one of the disadvantages of the mode is that for many sets of data, there may not be a distinct mode. In such cases, the data may have a uniform distribution where all values occur with equal frequency, or it may have multiple modes with similar frequencies.
The mode is not affected by extremely large or small values. It only considers the frequency of values and not their magnitude. Therefore, extreme values do not influence the mode.
The statement that the mode can only be computed for interval-level data or higher is incorrect. The mode can be computed for any type of data, including nominal, ordinal, interval, and ratio data. It is applicable to categorical as well as numerical data.
The main disadvantage of the mode is that for many datasets, there may not be a distinct mode.
The correct option is: For many sets of data there is no mode.
For more such questions on mode
https://brainly.com/question/14532771
#SPJ8
In a certainâ state, the recent average critical reading standardized test score was 514. Assume that the standard deviation is 50 and that standardized test scores are Normally distributed. Complete partsâ (a) andâ (b) below. Include a Normal curve for each part.
Required:
a. What percentage of standardized test takers scored 550 or less?
b. What percentage of standardized test takers scored 524?
Answers
Answer:
a) Percentage of standardized test takers that scored 550 or less = 76.4%
b) Percentage of standardized test takers that scored 524 = 0.782%
Step-by-step explanation:
This is a normal distribution problem with
Mean = μ = 514
Standard deviation = σ = 50
a) Percentage of standardized test takers scored 550 or less = P(x ≤ 550)
We first normalize or standardize 550
The standardized score for any is the value minus the mean then divided by the standard deviation.
z = (x - μ)/σ = (550 - 514)/50 = 0.72
To determine the required probability
P(x ≤ 550) = P(z ≤ 0.72)
We'll use data from the normal distribution table for these probabilities
P(x ≤ 550) = P(z ≤ 0.72) = 0.76424 = 76.424%
The normal curve for this question and the b part are sketched in the first attached image to this solution.
b) Percentage of standardized test takers that scored 524 = P(x = 524)
On standardizing,
z = (x - μ)/σ = (524 - 514)/50 = 0.20
For this part, since it's an exact probability, we will use the normal distribution formula
P(z = Z) = [1/(σ√2π)] × e^(-z²/2)
Since z = (x - μ)/σ
It can be written properly as presented in the second attached image to this question.
Putting x = 524 or z = 0.20 in this expression, we get
P(x = 524) = P(z = 0.20) = 0.0078208539 = 0.782%
Hope this Helps!!!


Enter your answer, rounded to the nearest tenth, in the box.

Answers
ANSWER:
-11.4
STEP-BY-STEP EXPLANATION:
We have the following function:
\(f\mleft(x\mright)=\frac{100}{-10+e^{-0.1x}}\)We calculate the result when x = -2, just like this:
\(\begin{gathered} f(-2)=\frac{100}{-10+e^{-0.1\cdot-2}} \\ f(-2)=\frac{100}{-10+e^{0.2}} \\ f(-2)=\frac{100}{-10+1.22} \\ f(-2)=\frac{100}{-8.78} \\ f(-2)=-11.4 \end{gathered}\)When x = -2, the value of the function is equal to -11.4
You have $4,500 to invest. Which plan would generate the most interest after three years?
OA. 5.0% compounded semi-annually
OB. 4.9% compounded quarterly
OC. 4.8% compounded monthly
OD 5.1% compounded yearly
Answers
Answer:
5.1% compounded yearly
Step-by-step explanation:
f(x) = 4500(1 + .05/2)^2(3) = 5218.62
f(x) = 4500(1+ .049/4)^4(3) = 5207.94
f(x) = 4500(1+ .048/12)^(12)(3) = 5195.49
f(x) = 4500(1 + .051/1)^1(3)= 5224.21
Answer:
D
Step-by-step explanation:
Find the volume of the prism below if each cube has a side length of 1/8 of a foot
Answers
Answer:
\(Volume = \frac{3}{128}ft^3\)
Step-by-step explanation:
Given
\(Length = 1\ cube\)
\(Width = 3\ cubes\)
\(Height = 4\ cubes\)
\(1\ cube = \frac{1}{8}ft\)
Required
The volume of the cube
Start by calculating the dimension in ft
\(Length = 1\ cube\)
\(Length = 1 * \frac{1}{8}ft\)
\(Length = \frac{1}{8}ft\)
\(Width = 3\ cubes\)
\(Width = 3 * \frac{1}{8}ft\)
\(Width = \frac{3}{8}ft\)
\(Height = 4\ cubes\)
\(Height = 4 * \frac{1}{8}ft\)
\(Height = \frac{1}{2}ft\)
So, the volume is:
\(Volume = Length * Width * Height\)
\(Volume = \frac{1}{8}ft * \frac{3}{8}ft * \frac{1}{2}ft\)
\(Volume = \frac{1}{8} * \frac{3}{8} * \frac{1}{2}ft^3\)
Using a calculator, we have:
\(Volume = \frac{3}{128}ft^3\)
Solve 1/3(3.2×1.4)2.8
Simplify your answer
Answers
Answer:
4.181
Step-by-step explanation:
1/3 (3.2×1.4) 2.8
1/3 ( 4.48) 2.8
1/3 (4.48 × 2.8)
1/3 × 12.544
= 4.181
If a permutation is chosen at random what is the probability that it begins with at least two A's
Answers
Answer:
Starting with AT LEAST 2 A's means starting with 3 A's, or starting with 2 A's with some different letter third.
P(AAA...) = (3/9)(2/8)(1/7) = 1/84
Step-by-step explanation:
PLEASE HELP ITS PRE CALC LUV U
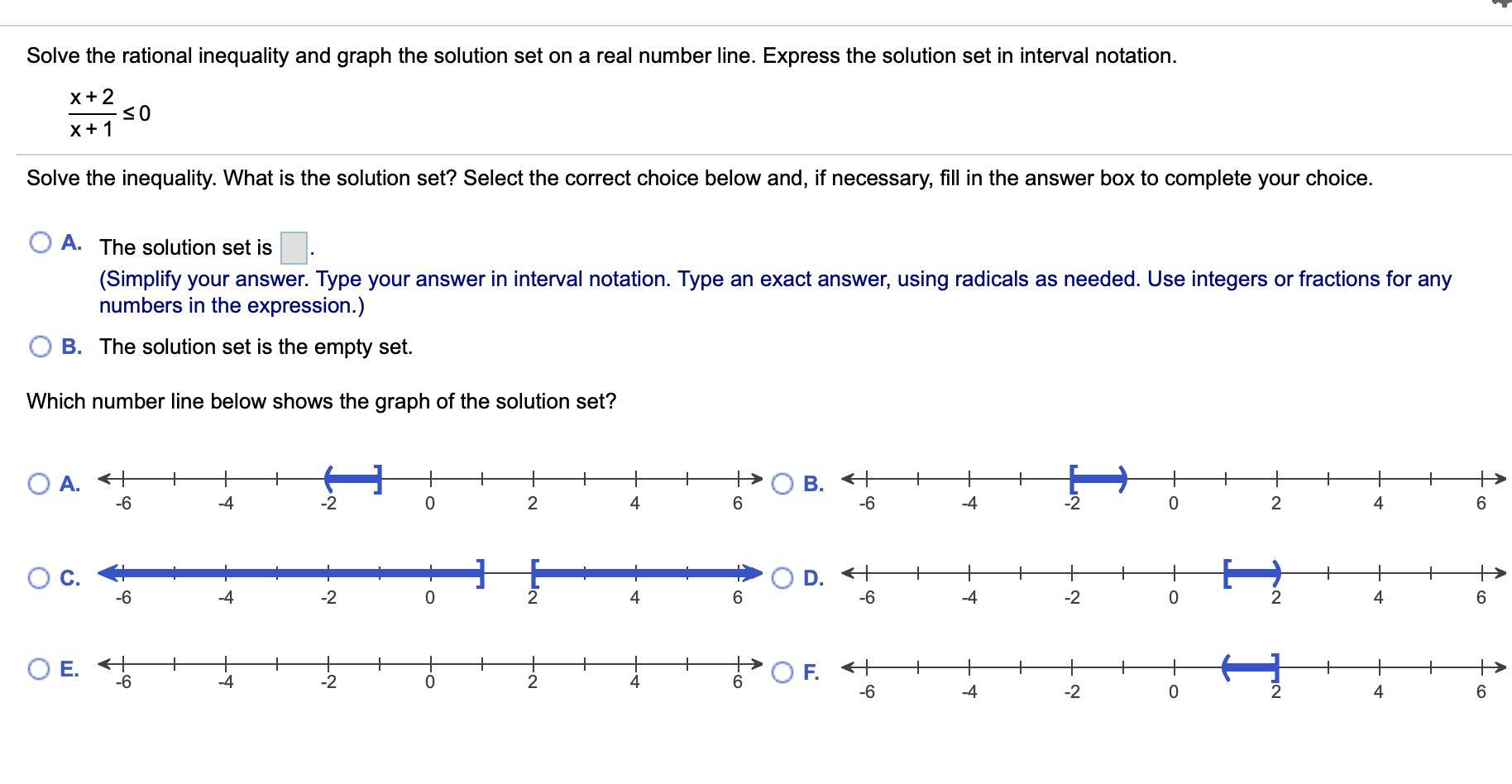
Answers
Answer:
Option A: -2≤x<-1
Step-by-step explanation:
Then select graph a
Answer: Anyway, option A.
Step-by-step explanation:
The Sweater Shop has a sweater that was original $55. It is now on sale for $32. What is the
decrease percent?
Answers
Answer:
52-32
Step-by-step explanation:
Carrie used 6 lemons to make 24 fluid ounces of lemonade. Carrie is having a big party and needs to make 288 fluid ounces of lemonade. How many leominster will she need to use in order to keep the recipe proportional?
A: 4
B: 264
C: 72
D: 48
Answers
Answer:
72
Step-by-step explanation:
PLSS HELP!!
Explain the process to simplify the rational expression including any domain restriction.
Explain why there are domain restrictions.
Simplify: 2x²+13x+20
———————
2x2+17x+30
Answers
the denominator will be zero when. \(x=-2\)or \(x=-7.\) Therefore, the domain of the expression is all real numbers except \(x=-2\) and \(x=-7\).
What is factor?In mathematics, factoring refers to the process of finding the factors of a given number or expression. Factors are numbers or expressions that can be multiplied together to obtain the original number or expression. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because these are the numbers that can be multiplied in pairs to obtain 12 (e.g. 2 x 6 = 12).
In algebra, factoring involves breaking down an algebraic expression into simpler expressions that can be multiplied together. This is done by finding common factors or using techniques such as difference of squares, perfect squares, or grouping. Factoring is an important tool in algebra, as it can help simplify complex expressions and solve equations.
To simplify a rational expression, follow these steps:
Step 1: Factor both the numerator and denominator if possible. For example, in the expression you provided, the numerator can be factored as\((2x+5)(x+4)\)and the denominator can be factored as \((2x+15)(x+2)\).
Step 2: Cancel out any common factors in the numerator and denominator. In this case, both the numerator and denominator have a common factor of (2x+5), which can be cancelled out.
Step 3: Simplify the remaining expression. After cancelling out the common factor, the simplified expression becomes:
\((2x+5)(x+4) / (2x+15)(x+2) = (x+4) / (x+2)(2x+15)\)
Domain restrictions occur when a value of x makes the denominator equal to zero, because division by zero is undefined. In this case, the denominator will be zero when x=-2 or x=-7. Therefore, the domain of the expression is all real numbers except x=-2 and x=-7.
It is important to identify any domain restrictions before simplifying a rational expression to ensure that the final expression is valid for all values of x in its domain.
To know more about denominator, visit:
https://brainly.com/question/17153086
#SPJ1
