Answers
Related Questions
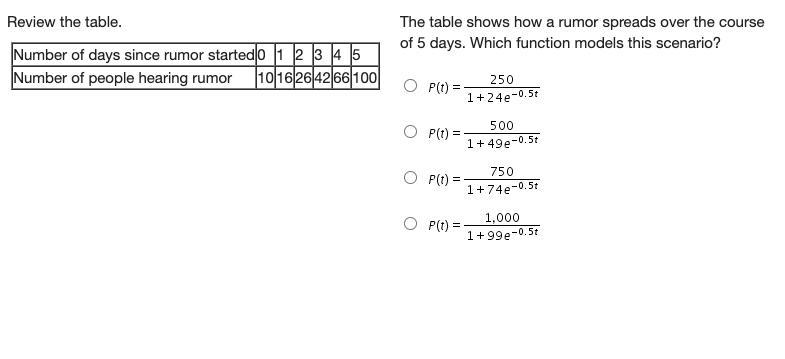
Review the table.
Number of days since rumor started 0 1 2 3 4 5
Number of people hearing rumor 10 16 26 42 66 100
The table shows how a rumor spreads over the course of 5 days. Which function models this scenario?
Answers
Answer:
The function that models the scenario is given as follows;
\(P(t) = \dfrac{500}{1 + 49 \cdot e^{-0.5 \cdot t}}\)
Step-by-step explanation:
The table of values are presented as follows;
The number of days, t, since the rumor started: 0, 1, 2, 3, 4, 5
The number of people, P, hearing the rumor: 10, 16, 26, 42, 66, 100
Imputing the given functions from the options into Microsoft Excel, and
\(A = P(t) = \dfrac{250}{1 + 24 \cdot e^{-0.5 \cdot t}}\)
\(B = P(t) = \dfrac{500}{1 + 49 \cdot e^{-0.5 \cdot t}}\)
\(C = P(t) = \dfrac{750}{1 + 74 \cdot e^{-0.5 \cdot t}}\)
\(D = P(t) = \dfrac{1000}{1 + 99 \cdot e^{-0.5 \cdot t}}\)
solving using the given values of the variable, t, we have;
P t A B \({}\) C D
10 \({}\) 0 \({}\) 10 \({}\) 10 \({}\) 10 \({}\) 10
16 \({}\) 1 \({}\) 16.07021 16.27604 16.34583 \({}\) 16.38095
26 \({}\) 2 \({}\) 25.43466 26.2797 26.574 26.72363
42 \({}\) 3 \({}\) 39.33834 41.89929 42.82868 43.30901
66 \({}\) 4 \({}\) 58.85058 65.51853 68.09014 69.45316
100 \({}\) 5 \({}\) 84.17395 99.55866 106.0177 109.5721
Therefore, by comparison, the function represented by \(B = P(t) = \dfrac{500}{1 + 49 \cdot e^{-0.5 \cdot t}}\) most accurately models the scenario.
Answer:
B: P (t) = 500/1 + 49 e^-0.5 t
Step-by-step explanation:
Took the review.

answer this question please in short time

Answers
Answer:
14256
Step-by-step explanation:
write the following in simplest form
A)12:33
B)20mm:5cm
Answers
A) 12 and 33 can be divided by 3 so 12:33 = 4:11
B= 20 and 5 can be divided by 5 so 20mm:5mm = 4mm:1mm
Answer:
A. 4: 11
B. 4: 1
Step-by-step explanation:
What are these? These are ratios, which show proportion. For example, for every two dogs, there is one cat. They can be written as words, fractions, or with colons, such as in these problems.
How to simplify: To simplify, think of the highest common factor. If you can't think of the highest, just think of a factor both numbers have in common and keep going until the numbers don't have any factors in common.
In this case, for A, the common factor was 3. 12/3=4 and 33/3=11. This cannot be simplified further because 11 is prime, which means it has no factors besides 1 and 11.
For B, the common factor was 4, so it is 4:1.
Can you have a triangle with 2cm 3cm 5cm Class 7?
Answers
No , we cannot have a triangle with 2cm , 3cm and 5cm , because the sum of two sides is not greater than the other sides .
What is a Triangle ?
A triangle can be defined as the closed figure , that is made up of three line segments .
The Condition for any three sides to form a triangle : the sum of any two sides of triangle should be greater than the third side .
The sides of triangle are given to be : 2cm , 3cm and 5cm ;
on adding the two sides ,
we get ;
⇒ 2 + 3 = 5 > 5 ; False
⇒ 3 + 5 = 8 > 2 ; True
⇒ 2 + 5 = 7 > 3 ; True
All the conditions are not met ,
Therefore , the given sides cannot form a triangle .
Learn more about Triangle here
https://brainly.com/question/13948245
#SPJ4
click the image for the question someone pls help i suck at algebra ill love u forever <3‼️

Answers
Answer:
$ 30,000
Step-by-step explanation:
c = 300 ³√n²
= 300× ³√1000²
= 300× 100
= 30,000
Answer: $30000
Step-by-step explanation:
\(300\sqrt[3]{n^2}\)
\(300\sqrt[3]{1000^2}\)
\(300\sqrt[3]{1000000}\)
300 × 100 = 30000
Help! My teacher never taught me this and gave it to me for what ever reason. Questions 6-11. (Middle school)

Answers
Answer:
6. 12cm
7. 11.2 cm
8. 92 degrees
9. 53 degrees
10. 37.5 cm
11. $ 693.12
Step-by-step explanation:
For questions 6-9 the triangle is congurent which means both their angles will be equal.
For the sides you can see that the second triangle is 1.5 times smaller than the first one as taking one of the sides 21/14= 1.5
So for Q. 6 we can multiply side PQ by 1.5.
For Q.7 divide CA by 1.5.
For Q. 10 we can do cross multiplication:
5/4 = x/30
= 150= 4x
= 37.5=x
For Q 11 we can see the size of the paper is 1.9 times bigger than the original one (38/20)
So the shorter side is 30.4 cm.
Then we have to find the area of the paper to multiply the two dimensions and we get 1155.2 square inches.
Then to figure out the money we multiply again and we get $693.12.
Jim is looking at the roof of a new house from the front. He notices that the roof is
triangular in shape with a base 13.6 m. The left side is 8.0 m long and makes an angle of 70 degrees with the base of the roof. If this is the only known information, determine the angle the right side of the roof makes with the base of the roof to the nearest degree. Be sure to first make a sketch.
Answers
The angle that the right side of the roof makes with the base of the roof to the nearest degree is 32 degrees.
What is the angle the right side of the roof makes with the base of the roof ?We know that a triangle is a three sided figure. The question shows us that the left side of the triangular roof is 8.0 m long and makes an angle of 70 degrees with the base of the roof. This base has a length of 13.6 m.
We can now make use of the cosine rule;
b^2 = a^2 + c^2 - 2ac cos B
a = 13.6
b = ?
c = 8
B = 70 degrees
Now;
b = √(13.6)^2 + (8)^2 - 2(13.6 * 8) cos 70
b = √184.96 + 64 - 2(108.8) * 0.3420
b = √184.96 + 64 - 44.42
b = 14.3
By the use of the sine rule;
b/sinB = c/sinC
14.3/sin70 = 8/sinC
14.3 * sinC = 8 * sin70
sinC = 8 * sin70/14.3
C = 32 degrees
The angle that the right side of the roof makes with the base of the roof to the nearest degree is 32 degrees.
Learn more about cosine rule:https://brainly.com/question/20839703
#SPJ1
The price of pears can be determined by the equation P=0.54n, where P is the price and n is the number of pears. What is the constant of proportionality (unit rate)?
PLEASE NEED THIS ASAP!!!!!!!!!!
Answers
Answer:
The constant of proportionality is 0.54
Step-by-step explanation:
Given:
P = 0.54n
Where,
P = price of pears
n = number of pears
What is the constant of proportionality (unit rate)?
The constant of proportionality is 0.54
This means a unit of pears cost $0.54
If the number of pears bought, n = 50
Then,
P = 0.54n
When n = 50
P = 0.54(50)
= 27
P = 27 when n = 50
The correct answer is:
The constant of proportionality is 0.54
What is another term that accountants use that means the same as "cost recovery"? 3. Why for every class of asset does the table list one additional year? For example, there are six years listed for 5-year property classes. 4. What are examples of assets that fall into the 5-year class? This and following questions relate to your basic understanding of non-tax depreciation from financial accounting. 5. If you bought an asset for $100 with a 5-year life and no residual value, how much would you depreciate each year under straight-line? 6. If you bought an asset for $100 with a 5-year live with no residual value, how much would you depreciate in years 1 through 5 under double-declining balance. Do not use the tables below. Round to nearest penny, and ensure that total is $100. Year 1 2 5
Answers
Another term that accountants use to refer to "cost recovery" is "cost reimbursement."
What is the alternative term for "cost recovery" used by accountants?In accounting, "cost recovery" refers to the process of recouping or recovering the expenses incurred by a company through various means such as sales revenue, reimbursements, or cost allocation.
Another term commonly used to describe this concept is "cost reimbursement." It signifies the reimbursement of costs to the company, ensuring that the expenses are covered and recovered, often through reimbursement agreements with clients or partners.
Read more about cost reimbursement
brainly.com/question/31930459
#SPJ1
5/4=y−14 help meeeee
Answers
Answer:
y= 61/4
Step-by-step explanation:
-y=-14-5/4
-y=-61/4
-1(-y=-61/4)
y= 61/4
What’s the surface area of a sphere if the radius is is 15cm?
Answers
Answer :
2827.43 cm²
Step-by-step explanation:
1/5/2023
7:20PM
Answer:
2827.4 cm²
Step-by-step explanation:
A = 4πr²
A = 4π(15)² = 2827.4 cm²
What is the only prime number HURRY
Answers
A metal worker wants to figure out the cost of making a rectangular iron bar. He knows that the required dimensions of the bar are 8. 0 cm (width), 0. 40 cm (height), and 310 cm (length). If this kind of iron costs $0. 015 per cm3, what is the cost of making the bar (to the nearest dollar)? $5 $15 $37 $93.
Answers
The cost of making the rectangular iron bar is $37.
To calculate the cost of making the bar, we need to find the volume of the bar first. The volume of a rectangular prism can be calculated by multiplying its length, width, and height. In this case, the volume of the bar is 8.0 cm * 0.40 cm * 310 cm = 992 cm^3.
Next, we multiply the volume by the cost per cm^3, which is $0.015. So, the cost of making the bar is 992 cm^3 * $0.015/cm^3 = $14.88.
Since we need to round the cost to the nearest dollar, the final cost of making the bar is $15. Therefore, the correct answer is $37.
Learn more about volume here: brainly.com/question/12165015
#SPJ11
It says shade 3/4 of this figure

Answers
3*2/4*2=6/8
Answer:
I think you shade in 6 of the rectangles
can somebody help me with these three problems? i'm having a bit of trouble getting the right answer and i don’t really understand what i am doing.

Answers
Explanation/Answer:
To convert, we need a common denominator.
So if, say, we multiply the denominator by 2, we must multiply the numerator by 2 as well.
1) 4/5+4/7
4x7/5x7 + 4x5/7x5
28/35+20/35
(Both have common denominators so we can add them)
28 +20/35= 48/35=1 13/35
2) 1/2+11/8
(We already have common denominator in one of the numbers so we only have to convert ONE of the fractions)
1x4/2x4+11/8
4/8+11/8=15/8= 1 7/8
3) 1/5+1/3
1x3/5x3+1x5/3x5
3/15+5/15=8/15
Hope this helped :D
Answer:
1. 48/35
2. 15/8
3. 8/15
Step-by-step explanation:
You have to make sure the denominator is the same before combining both fractions. Whatever you multiply by the denominator, you need to do to the numerator.



Which trigonometric function would you use to find x

Answers
Answer:
law of sines
Step-by-step explanation:
a over sinA = b over sinB
Revenue given by R(q)=600q and cost is given C(q)=10,000+5q2. At what quantity is profit maximized? What is the profit at this production level? 4= Proft =S
Answers
At the production level of 40 units, profit is maximized and the profit at this production level is $64,000.
Revenue is given by R(q) = 600q and cost is given by C(q) = 10,000 + 5q2. Profit is given by P(q) = R(q) - C(q).Therefore, P(q) = 600q - (10,000 + 5q2) or P(q) = -5q2 + 600q - 10,000. The profit is maximized at the production level where the derivative of P(q) is equal to zero.The derivative of P(q) is given by P'(q) = -10q + 600. Setting this to zero, we get -10q + 600 = 0 or q = 60. However, this is the maximum point of the revenue function R(q) and not the profit function P(q).To determine the maximum point of P(q), we need to find the second derivative of P(q) which is given by P''(q) = -10. Since P''(q) is negative, the maximum point of P(q) occurs at the production level q = 40. At q = 40, P(q) = -5(40)2 + 600(40) - 10,000 = $64,000.
Know more about profit here:
https://brainly.com/question/32537157
#SPJ11
Introductory Statistics Course Withdrawals. A university found that 20% of its students withdraw without completing the introductory statistics course. Assume that 20 students registered for the course. a. Compute the probability that 2 or fewer will withdraw. b. Compute the probability that exactly 4 will withdraw.
Answers
The probability that exactly 4 students will withdraw is approximately 0.2048.
The problem asks us to calculate the probabilities related to student withdrawals in an introductory statistics course. We are given that 20% of students withdraw from the course and that 20 students registered for the course.
a. To compute the probability that 2 or fewer students will withdraw, we need to calculate the cumulative probability of the binomial distribution. We can use the binomial probability formula:
P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)
Using the formula, the probability can be calculated as follows:
P(X = 0) = (20 choose 0) * (0.2^0) * (0.8^20) ≈ 0.0115
P(X = 1) = (20 choose 1) * (0.2^1) * (0.8^19) ≈ 0.0729
P(X = 2) = (20 choose 2) * (0.2^2) * (0.8^18) ≈ 0.1948
Therefore, P(X ≤ 2) ≈ 0.0115 + 0.0729 + 0.1948 ≈ 0.2792
b. To compute the probability that exactly 4 students will withdraw, we use the binomial probability formula:
P(X = 4) = (20 choose 4) * (0.2^4) * (0.8^16) ≈ 0.2048
Therefore, the probability that exactly 4 students will withdraw is approximately 0.2048.
Learn more about binomial probability here: https://brainly.com/question/12474772
#SPJ11
Could someone please help meh? I’m testing and I need help x-x
Rewards- Brainliest and 15+

Answers
Answer:
19$
Step-by-step explanation:
16 + 10 = 26 + 5 = 31
he wins 50
50 - 31 = 19
He's left with 19 dollars out of 50 after he pays everyone back .
Answer:
D) 19
Step-by-step explanation:
Add 5+10+16=31
Subtract 50-31=19
I bought a 30 pack of water $10.56 dollars.How much was 1 bottle?
Answers
The cost of 1 bottle is equal to $0.35 according to the simple equation calculations.
Given,
Cost of 30 water bottles = $10.56 dollars
Cost of a single water bottle = ? ( x )
Lets simplify the given question.
30 = $10.56
1 = ? (x)
Cross multiply the above sum and convert into equation
30 (x) = (10.56 * 1) $
30 x = 10.56
x = 10.56 / 30 $
x = 0.35
Therefore, cost of a single water bottle from the quantity of 30 bottles is equal to $0.35 dollars.
Learn more about quantities:
https://brainly.com/question/27027328
#SPJ1
Making a pyrmid with four triangular sides and a square base the scal modle is 1:1000 how amny sides should the model pyrmid have
Answers
The base of the pyramid is a square, which has four sides and each triangular side forms an individual side of the pyramid, resulting in a total of four triangular sides. The model pyramid should have a total of five sides.
A pyramid with four triangular sides and a square base consists of a total of five sides. The base of the pyramid is a square, which has four sides. Additionally, each triangular side forms an individual side of the pyramid, resulting in a total of four triangular sides. Therefore, the model pyramid should have a combined total of five sides.
The scale model being 1:1000 means that the dimensions of the model are 1000 times smaller than the actual pyramid. In other words, every unit of measurement in the model represents 1000 units in the real pyramid.
While the scale factor affects the dimensions and proportions of the pyramid, it does not change the number of sides. Hence, regardless of the scale, the pyramid will always have four triangular sides and one square base, totaling five sides.
Learn more about pyramid here:
https://brainly.com/question/27915682
#SPJ11
What is the diameter of the circle given the equation

Answers
Answer:
C
Step-by-step explanation:
Correct me if i'm wrong-.
I need help with this

Answers
1. Since triangle ABC and DEF are congruent, the value of x is -3
2. length AB = 24
length DE = 24
What are congruent triangles?If the three angles and the three sides of a triangle are equal to the corresponding angles and the corresponding sides of another triangle, then both the triangles are said to be congruent.
Since triangle ABC is congruent to triangle DEF , then we can say that line AB is equal to line DE
therefore;
12- 4x = 15-3x
collect like terms
12 -15 = -3x +4x
x = -3
therefore the value of x is -3 and
AB = 12 - 4x
AB = 12 -4( -3)
AB = 12 +12 = 24
DE = 15-3x
= 15-3(-3)
= 15 + 9
= 24
learn more about congruent triangles from
https://brainly.com/question/2938476
#SPJ1
Can you pleas help me with both!!!!!!!!!!!!!!!!!!!!


Answers
The difference in the values of the two cars when they are each 7 years old is equal to $6,000.
How to calculate the slope of a line?In order to determine the difference in the values of the two cars, we would have to write an equation that models the price of the cars after a length of time, by using the data points shown in the graph above.
Mathematically, the slope of any straight line can be calculated by using this formula;
Slope, m = (Change in y-axis, Δy)/(Change in x-axis, Δx)
Slope, m = (y₂ - y₁)/(x₂ - x₁)
For Car A, we have:
Slope, m = (y₂ - y₁)/(x₂ - x₁)
Slope, m = (9 - 12)/(4 - 2)
Slope, m = -3/2
Slope, m = -1.5
At point (4, 9), a linear equation for car's value can be calculated by using the point-slope form:
y - y₁ = m(x - x₁)
Where:
m represents the slope.x and y represent the points.c represent the y-intercept.Substituting the given points into the formula, we have;
y - y₁ = m(x - x₁)
y - 9 = -1.5(x - 4)
y = -1.5x + 15
In 7 seven years, the value of Car A is given by:
y = -1.5x + 15
y = -1.5(7) + 15
y = $4,500
Note: The negative sign indicates that the value of the car is depreciating.
For Car B, we have:
Slope, m = (y₂ - y₁)/(x₂ - x₁)
Slope, m = (10 - 18)/(5 - 1)
Slope, m = -8/4
Slope, m = -2
At point (5, 1), a linear equation for car's value can be calculated by using the point-slope form:
y - y₁ = m(x - x₁)
y - 1 = -2(x - 5)
y = -2x + 11
In 7 seven years, the value of Car B is given by:
y = -2x + 11
y = -2(7) + 3.5
y = $10,500
Now, we can determine the difference as follows:
Difference = $10,500 - $4,500
Difference = $6,000.
Read more on slope here: brainly.com/question/3493733
#SPJ1
Use polar coordinates to find the volume of the given solid. Inside the sphere x^2 + y^2 + z^2 = 36 and outside the cylinder x^2 + y^2 = 1.
Answers
The required volume of the given solid is (√16 - r²) -(-√16 - r²).
What is volume?The measurement of three-dimensional space is volume. It is frequently expressed quantitatively using SI-derived units, as well as several imperial or US-standard units.
Volume and the notion of length are connected.
Volume, which is measured in cubic units, is the 3-dimensional space occupied by matter or encircled by a surface.
The cubic meter (m3), a derived unit, is the SI unit of volume.
So, the integrand often takes the form z upper z lower, where z stands for the solid's lower and upper borders.
We are treating the sphere as a hemisphere as of right now, with the XY-plane serving as its lower boundary. Consequently, you must multiply by 2.
The solid's volume is (√16 - r²) -(-√16 - r²).
Therefore, the required volume of the given solid is (√16 - r²) -(-√16 - r²).
Know more about volume here:
https://brainly.com/question/29665831
#SPJ4
Correct question:
Use polar coordinates to find the volume of the given solid: Inside the sphere x^2 + y^2 + z^2 = 16 and outside the cylinder x^2 + y^2 = 4.
bus 1 leaves at 8 am at 80 mph from point b to point a, 550 miles away. bus 2 leaves point a at 8:30am to point b at 90 mph. what time will they pass each other?
Answers
The bus 2 will pass bus 1 at 12.30 pm, when both are at 360 miles.
The bus 1 starts half hour earlier than bus 2. But since bus 2 is faster, it will overtake at some point. At 8 am, bus 1 will start. By the time 8.30, it will cover a distance of 40 miles.
Bus 2 starts at 8.30, So it will be at 0 miles.
By 10, the bus 1 will be at 160 miles, bus 2 at 135 miles
By 10.30, the bus 1 will be at 200 miles, bus 2 at 180 miles.
By 11.30, bus 1 will be at 280 miles, bus 2 will be at 270 miles
By 12.30, bus 1 will be at 360 miles, bus 2 will be at 360 miles.
So at the 360 the, the both the buses passes each other.
For learning more about relative speeds, kindly refer
https://brainly.com/question/14581650
#SPJ4
Find the angle between the vectors. (Round your answer to two decimal places.) u = (-3,-4), v = (5,0), (u, v) = 3u1V1 + u2V2. Ꮎ = _____ radians. Find the angle 8 between the vectors. 3T u = (cos 3phi/4, sin 3phi/4). v = cos phi/6, sin phi/6). Ꮎ = ______ radians
Answers
The angle between vectors u and v is approximately 2.21 radians and the angle 8 between vectors 3Tu and v is |15phi/12|
First, we need to find the dot product of vectors u and v:
u · v = (-3)(5) + (-4)(0) = -15
Then, we can find the magnitudes of the vectors:
|u| = √\(((-3)^2 + (-4)^2)\)= 5
|v| = √\((5^2 + 0^2)\) = 5
Using the formula for the angle between two vectors:
cos θ = (u · v) / (|u||v|)
cos θ = (-15) / (5 * 5) = -0.6
θ = arccos(-0.6) ≈ 2.21 radians
Therefore, the angle between vectors u and v is approximately 2.21 radians.
For the second part of the question:
First, we need to find the dot product of vectors 3Tu and v:
3Tu · v = (3cos(3phi/4))(cos(phi/6)) + (3sin(3phi/4))(sin(phi/6))
3Tu · v = 3(cos(3phi/4)cos(phi/6) + sin(3phi/4)sin(phi/6))
Using the trigonometric identity cos(a-b) = cos(a)cos(b) + sin(a)sin(b), we can simplify the dot product:
3Tu · v = 3cos(3phi/4 - phi/6)
Then, we can find the magnitudes of the vectors:
|3Tu| = √(\((3cos(3phi/4))^2 + (3sin(3phi/4))^2\)) = 3√2
|v| = √(\((cos(phi/6))^2 + (sin(phi/6))^2\)) = 1
Using the formula for the angle between two vectors:
cos θ = (3Tu · v) / (|3Tu||v|)
cos θ = [3cos(3phi/4 - phi/6)] / (3√2)
cos θ = cos(15phi/12)
θ = arccos(cos(15phi/12)) = |15phi/12|
Therefore, the angle 8 between vectors 3Tu and v is |15phi/12|.
To know more about vectors refer here:
https://brainly.com/question/29740341
#SPJ11
Select three collinear points.

Answers
Answer:
P,T,R
Step-by-step explanation:
Collinear points are along the same line
PTR are along the same line
(1 point) If f(x) = x2 + 2, find and simplify the following:(a) f(t + 2)(b) f(t^3+ 2) =(d) 3f(t)(e) (f(t))^2 + 2 =
Answers
Consider the function f(x) = (x)^2+2 which is equivalent to the given function. In here, we are taking whatever is inside the the parenthesis , we raise it to the power of 2 and then add 2. Note that if we change the x for a t, we will get f(t) = (t)^2+2 which is essencially the same thing.
To solve this question we will use the following formula
\((a+b)^2=a^2+2ab+b^2\)So, now we simply replace and simplify:
\(f(t+2)=(t+2)^2+2=t^2+2t+2^2+2=t^2+2t+4\)\(f(t^3+2)=(t^3+2)^2+2=t^6+2t^3+4+2=t^6+2t^3+6\)\(3f(t)=3(t^2+2)=3t^2+3\cdot2=3t^2+6\)\((f(t))^2+2=(t^2+2)^2+2=t^4+2t^2+4+2=t^4+2t^2+6\)Consider three random variables, U, V, and W. Suppose we know that U = 3V+2 and U = 5W – 23. If E(V) = -5, evaluate E(W). OA-13 13 OB- OC.-3 36 OD 5 O E 2
Answers
Consider three random variables, U, V, and W. The answer is E(W) = 2.
To solve for E(W), we need to use the fact that U is equal to both 3V+2 and 5W-23. We can set these two expressions equal to each other:
3V + 2 = 5W - 23
Solving for V in terms of W, we get:
V = (5W - 25) / 3
Now we can use the formula for the expected value of a linear function of a random variable:
E(aX + b) = aE(X) + b
In this case, we have:
V = (5W - 25) / 3
So:
E(V) = E((5W - 25) / 3) = (5/3)E(W) - 25/3
We know that E(V) = -5, so we can substitute that in:
-5 = (5/3)E(W) - 25/3
Solving for E(W), we get:
E(W) = (-5 + 25/3) / (5/3) = 2
Know more about expected value here:
https://brainly.com/question/29574962
#SPJ11
