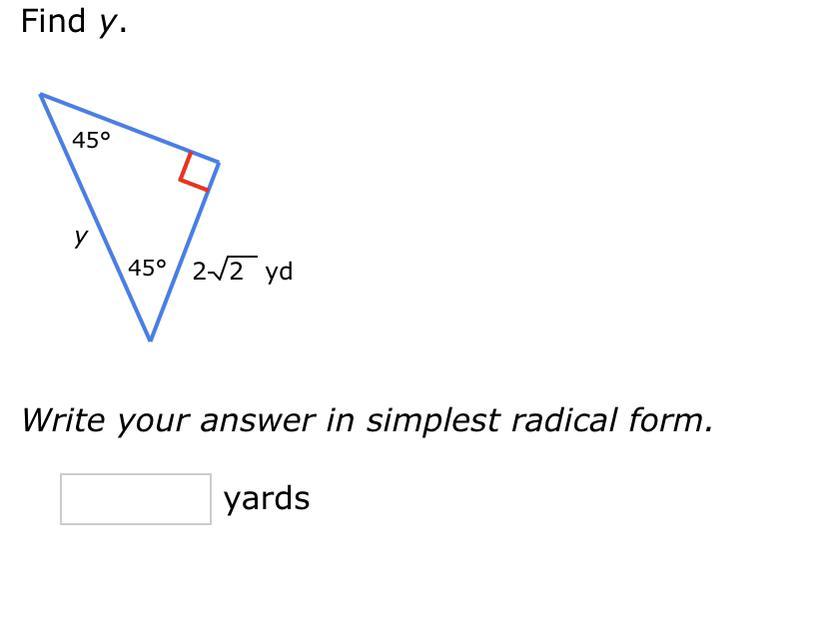
Answers
The value of y in the triangle is 4 yd
How to find the value of y?Trigonometry deals with the relationships between the sides and angles of triangles.
The three primary trigonometric functions are sine (sin), cosine (cos), and tangent (tan), which relate the ratios of the sides of a right triangle to its angles.
Using trigonometric function:
sin 45° = (2√2)/y (sine = opposite/hypotenuse)
2/√2 = (2√2)/y
y = (2√2) / (2/√2)
y = 4 yd
Thus, the value of y is 4 yd.
Learn more about Trigonometry on:
brainly.com/question/11967894
#SPJ1
Related Questions
What is the exponential form of root 2?
Answers
The Exponential Form of the number root 2 , is represented as \((2)^{\frac{1}{2} }\) , because the term "root" means the exponent is \(\frac{1}{2}\) .
The Root of a number x ; is defined as another number, which when multiplied by itself by given number of times is equal to x .
The Square Root of a "number x" is ; denoted by symbol "\(\sqrt{x}\)" .
we have to express the number root 2 in exponential form ;
So, we write root 2 as ⇒ \(\sqrt{2}\) ;
we know that the square root of any number x , in exponential form is written as \(x^{\frac{1}{2} }\) ;
So , the exponential form of root 2 is \((2)^{\frac{1}{2} }\) .
Learn more about Exponential Form here
https://brainly.com/question/13290418
#SPJ4
I need help finding the answer
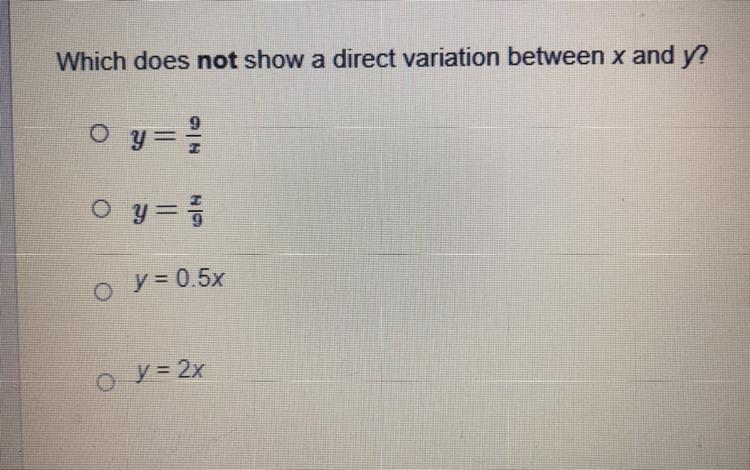
Answers
I guess option A is the correct answer
Emery borrowed money from her brother to buy a new phone and is paying off a fixed amount each week. After 2 weeks, she will owe $456, and after 5 weeks, she will owe $228.
a. Write an equation in point-slope form to represent the situation.
b. What was the original amount Emery owed?
608$
c. How much is being paid each week?
76$
I only need the answer to question 1
Answers
Answer:
A. $608 B. $76
Hope this helps
Answer:
\(y=5w+2w=228\)
Step-by-step explanation:

Please help!
I really need it asap

Answers
If it takes 4 men 6 hours to repair a road, how long will it take 7 men to do the job if they work at the same rate?
2
3 hours
x A
4x
4x
B
C
D
5
3/1/724
3 hours
4/7/1
hours
3
3 hours
7
E 2 hours
Answers
It will take 7 men 42 hours to complete the job if they work at the same rate.
If it takes 4 men 6 hours to repair a road, it means that the total work done is 1 job.
The number of man-hours required to complete the job is the product of the number of men and the number of hours
= 4 men x 6 hours
= 24 man-hours
Now, let's find out how many hours it will take for 7 men to do the same job. We can set up a proportion using the man-hours:
4 men / 24 hours = 7 men / x hours
4x = 7 (240)
4x = 168
x = 168 / 4
x = 42
Therefore, it will take 7 men 42 hours to complete the job if they work at the same rate.
Learn more about Proportion here:
https://brainly.com/question/26974513
#SPJ1
a ball is dropped form a height of 75 feet and bouces 30% of its previous height on each bounce. how high will its 5th bounce be
Answers
The ball will bounce up to a height of approximately 2.92 feet on its 5th bounce.
When a ball is dropped from a height of 75 feet and bounces, it follows a pattern where it bounces back up to a percentage of its previous height. In this case, the ball bounces up to 30% of its previous height on each bounce.
To find out how high the ball will bounce on its 5th bounce, we can use a simple formula. We start with the original height of 75 feet and multiply it by the percentage of the bounce, which is 30%, raised to the power of the number of bounces, which is 5 in this case.
So, the formula looks like this:
75 x (0.3)^5 = 2.9245 feet
Therefore, the ball will bounce up to a height of approximately 2.92 feet on its 5th bounce. It's important to note that the height of each bounce will continue to decrease by 30% of the previous height, so the ball will eventually come to a stop.
Understanding the bounce pattern of a ball can be helpful in predicting its trajectory and height, which can be useful in various sports and scientific experiments.
Learn more about percentage brainly.com/question/29306119
#SPJ11
Halpppp meee Brainliest
Correct answer pleaseee andd tyy

Answers
Answer:
\(12 {x}^{3} + 2 {x}^{2} - 25x - 14\)
Step-by-step explanation:
\((3x + 2)(4 {x}^{2} - 2x - 7)\)
\(12 {x}^{3} - 6 {x}^{2} - 21x + 8 {x}^{2} - 4x - 14\)
\(12 {x}^{3} + 2 {x}^{2} - 25x - 14\)
Goran needs to buy plastic spoons. Brand A has a box of 42 spoons for $1.49. Brand B has a box of 96 spoons for $4.98.
Find the unit price for each brand. Then state which brand is the better buy based on the unit price.
Round your answers to the nearest cent.

Answers
Answer:
Brand A : $0.04 , Brand B : $0.05.. In my opinion i would go for brand b because for 1 cent more you get 54 more spoons.
Step-by-step explanation:
By using the division method,
The unit price of the Brand A spoon is $0.035
And, the unit price of the Brand B spoon is $0.052
Used the concept of division for finding the unit price for each brand which states that,
The division method is used to distribute a group of things into equal parts. The division is just the opposite of multiplications.
Given that,
Goran needs to buy plastic spoons.
Brand A has a box of 42 spoons for $1.49.
And, Brand B has a box of 96 spoons for $4.98.
Hence, the unit price of the Brand A spoon,
\(\dfrac{\$1.49}{42}\)
\(= \$0.035\)
And, the unit price of the Brand B spoon,
\(\dfrac{\$4.98}{96}\)
\(= \$0.052\)
To learn more about the divide visit:
https://brainly.com/question/28119824
#SPJ4
What x value solves the equation? 3x - 5 = 1
Answers
Answer:
2
Step-by-step explanation:
Answer:
x equals 2
Step-by-step explanation:
What is 4x + 11 < -21 on a number line
Answers
Answer: x <- -8
x is less than negative eight.
Step-by-step explanation:
First, subtract 11 from both sides. Then divide both sides by 11. The arrow should be open and pointing to the left.
Answer:
x <- -8
Step-by-step explanation:
Find X. round to nearest tenth using law of cosines, please help!

Answers
Step-by-step explanation:
Using the modified picture attached to this answer;
Parameters
x = Angle X
8 = x
19 = y
14 = z
Therefore,
Using Cosine rule
x² = y² + z² - 2·y·z·cos X
Masking Cos X the subject of the formula,
Cos X = (y² + z² - x²) / (2·y·z)
Cos X = (19² + 14² - 8²) / (2·19·14)
Cos X = (361 + 196 - 64) / 532
Cos X = (557 -64) / 532
Cos X = 493 / 532
Cos X = 0.92669
But, since we are looking for angle X, we have to divide both sides by Cos, therefore having;
X = Cos-¹ [0.92669]
Since 1 / Cos = Cos-¹
Therefore,
X = 22.075
And since x, our unknown, is equal to angle X, then,
x = 22.1 (to the nearest tenth)

One leg of an isosceles right triangle measures 5 inches. Rounded to the nearest tenth, what is the approximate length of the hypotenuse?
A: 2.5 inches
B: 5.0 inches
C: 7.1 inches
D: 9.8 inches
Answers
Sq root of 50=7.07 or 7.1 rounded to nearest tenth so your answer is C: 7.1 inches
Find the equation of a line parallel to y + 9 = -3/2x that passes through the point (-8,9)

Answers
slope intercept form:
y = mx + b (where m = slope
and b = y-intercept)
simply subtract 9 from both sides of the given equation to get slope intercept form of the first line:
y + 9 = -3/2x
y + 9 - 9 = -3/2x - 9
y = -3/2x - 9
so the slope (m) = -3/2
the problem tells us a point on the second line (x,y) or (-8,9)
and we now know slope is -3/2
so let’s plug those in and solve for the y-intercept (b) of the second line.
y = mx + b
9 = -3/2(-8) + b
9 = 12 + b
9 - 12 = 12 - 12 + b
-3 = b
so now we know the slope (m) of both lines is -3/2 and the y-intercept (b) of the second line is -3
all we have to do is use the information to establish slope intercept form of the equation of the second line:
y = mx + b
y = -3/2x - 3
The answer is: y = -3/2x - 3
check your answer by plugging the point (-8,9) back in to your equation
9 = -3/2(-8) - 3
9 = 12 - 3
9 = 9 [TRUE]
AB is a straight line. Work out the size of angle k

Answers
Answer:
35°
Step-by-step explanation:
180 degrees is the total sum of the angles in a triangle.
180° - 130° = 50°
180° - 85° = 95°
50° + 95° = 145°
180° - 145° = 35°
Which word is associated with multiplication when computing probabilities? Choose the correct answer below Disjoint O And O Not
Answers
When we calculate probabilities involving one event AND another event occurring, we multiply their probabilities.
According to me , independent is the word which is associated with multiplication when computing probabilities . Because when the events are independent then we multiply the probabilities .
According to the multiplication rule of probability, the probability of occurrence of both the events A and B is equal to the product of the probability of B occurring and the conditional probability that event A occurring given that event B occurs.
The probability of the union of two events is equal to the sum of individual probabilities. The union of two set contains all the elements of previous sets. The union is denoted by ∪. The equation for the students earnings will be expressed as P(A∪B). The occurrence of event A changes the probability of B then the events are dependent. If the probability of two events happening together is zero then the events are mutually exclusive.
Therefore,
When we calculate probabilities involving one event AND another event occurring, we multiply their probabilities.
To learn more about Probability visit :
brainly.com/question/13490624
#SPJ4
What is the slope of the line that passes through the points (-9, -3) (1 , -3)
Answers
Answer:
Slope is 0
Step-by-step explanation:
Slope is the change in the y coordinate over the change in the x coordinate so:
(-3 - -3)/ (1 - -9) = 0/10
this is a horizontal line
suppose y varies directly as x and y = 21 when x = 3. find y when x =2
Answers
Answer:
If y varies directly as x, then we can express this relationship using a proportionality constant k, such that:
y = kx
To solve for k, we can use the initial condition given:
y = 21 when x = 3
Substituting these values into the equation above, we get:
21 = k * 3
Solving for k, we get:
k = 7
Now that we have k, we can use the equation to find y when x = 2:
y = kx
y = 7 * 2
y = 14
Therefore, when x = 2, y = 14.
Step-by-step explanation:
Which of the following results in the difference of two squares?
a. (7x - 3y)^2
b. (4x - 9y)(4x - 9y)
c. 5x^2(4x - 3)
d. (2x + 8y)(2x - 8y)
Answers
Answer:d
Step-by-step explanation:
Write an equation and then solve.

Answers
2x + 3x + 6 + 2x + 6 = 33
7x + 12 = 33
7x = 21, x = 3
Plug into the lines
Line AB = 2(3) = 6 inches
Line AC = 3(3+2)= 15 inches
Line BC = 2(3+3) = 12 inches
derive the slope for drinks in the simple regression from the slope for drinks in the multiple regression. in other words show how you get from:
Answers
To derive the slope for a single variable regression from the slope in a multiple regression, you can use the concept of partial derivatives.
In a multiple regression model, we have several independent variables (predictors) that are used to predict a dependent variable. Let's say we have a multiple regression model with two independent variables: X1 and X2, and a dependent variable Y. The regression equation can be written as:
Y = b0 + b1X1 + b2X2
To find the slope for the variable X1, we need to hold all other variables constant and differentiate the regression equation with respect to X1. The partial derivative of Y with respect to X1 (denoted as ∂Y/∂X1) gives us the slope for X1 in the multiple regression model.
∂Y/∂X1 = b1
Therefore, the slope for X1 in the multiple regression is simply equal to b1, the coefficient of X1 in the regression equation.
So, to derive the slope for X1 in the simple regression model, you can directly use the coefficient b1 obtained from the multiple regression analysis.
To know more about variable visit-
brainly.com/question/28461635
#SPJ11
A project has an initial cost of $30 million.The project is expected to generate a cash flow of $2.85 million at the end of the first year.All the subsequent cash flows will grow at a constant growth rate of 3.85% forever in future.If the appropriate discount rate of the project is 11%,what is the profitability index of the project? a.1.917 b.1.328 c.1.387 d.1.114 ortcehov e. None of the above
Answers
Profitability index is 1.387. Thus, the correct option is (c) 1.387.
The formula for calculating the profitability index is:
P.I = PV of Future Cash Flows / Initial Investment
Where,
P.I is the profitability index
PV is the present value of future cash flows
The initial investment in the project is $30 million. The cash flow at the end of the first year is $2.85 million.
The present value of cash flows can be calculated using the formula:
PV = CF / (1 + r)ⁿ
Where,
PV is the present value of cash flows
CF is the cash flow in the given period
r is the discount rate
n is the number of periods
For the first-year cash flow, n = 1, CF = $2.85 million, and r = 11%.
Substituting the values, we get:
PV = 2.85 / (1 + 0.11)¹ = $2.56 million
To calculate the present value of all future cash flows, we can use the formula:
PV = CF / (r - g)
Where,
PV is the present value of cash flows
CF is the cash flow in the given period
r is the discount rate
g is the constant growth rate
For the subsequent years, CF = $2.85 million, r = 11%, and g = 3.85%.
Substituting the values, we get:
PV = 2.85 / (0.11 - 0.0385) = $39.90 million
The total present value of cash flows is the sum of the present value of the first-year cash flow and the present value of all future cash flows.
PV of future cash flows = $39.90 million + $2.56 million = $42.46 million
Profitability index (P.I) = PV of future cash flows / Initial investment
= 42.46 / 30
= 1.387
Therefore, the correct option is (c) 1.387.
Learn more about Profitability index
https://brainly.com/question/30641835
#SPJ11
let f ( x ) = { 10 − x − x 2 if x ≤ 2 2 x − 3 if x > 2 f(x)={10-x-x2ifx≤22x-3ifx>2 use a graph to determine the following limits. enter dne if the limit does not exist.
Answers
In summary, the limits of the function f(x) are as follows: lim(x→2-) f(x) = 2, lim(x→2+) f(x) = 1, lim(x→∞) f(x) = ∞, lim(x→-∞) f(x) = -∞
To determine the limits of the function f(x) as x approaches certain values, we can plot the graph of the function and observe the behavior. Let's analyze the limits of f(x) as x approaches different values.
First, let's plot the graph of the function f(x):
For x ≤ 2, the graph of f(x) is a downward-opening parabola that passes through the points (2, 0) and (0, 10). The vertex of the parabola is located at x = 1, and the curve decreases as x moves further away from 1.
For x > 2, the graph of f(x) is a linear function with a positive slope of 2. The line intersects the y-axis at (0, -3) and increases as x moves further to the right.
Now, let's analyze the limits:
Limit as x approaches 2 from the left: lim(x→2-) f(x)
Approaching 2 from the left side, the function approaches the value of 10 - 2 - 2^2 = 2. So, lim(x→2-) f(x) = 2.
Limit as x approaches 2 from the right: lim(x→2+) f(x)
Approaching 2 from the right side, the function follows the linear segment 2x - 3. So, lim(x→2+) f(x) = 2(2) - 3 = 1.
Limit as x approaches positive infinity: lim(x→∞) f(x)
As x approaches positive infinity, the linear segment 2x - 3 dominates the function. Therefore, lim(x→∞) f(x) = ∞.
Limit as x approaches negative infinity: lim(x→-∞) f(x)
As x approaches negative infinity, the parabolic segment 10 - x - x^2 dominates the function. Therefore, lim(x→-∞) f(x) = -∞.
These limits are determined by observing the behavior of the function as x approaches different values and analyzing the graph of the function.
Learn more about limits at: brainly.com/question/12211820
#SPJ11
7) [10 points] Find the Maclaurin series for the function f (x ) = In (1+x"").
Answers
The Maclaurin series expansion for ln(1+x) is:
ln(1+x) \(=x - \frac{1}{2}x^2 + \frac{1}{3}x^3 + ...\)
What is the maclaurin series?
The Maclaurin series is a special case of the Taylor series expansion where the expansion is centered around x = 0. It is a representation of a function as an infinite sum of terms involving powers of x, with coefficients determined by the derivatives of the function at x = 0.
The general formula for the Maclaurin series expansion of a function f(x) is:
\(f(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + ...\)
To find the Maclaurin series for the function f(x) = ln(1+x), we can use the Taylor series expansion.
The general formula for the Maclaurin series expansion of a function is:
\(f(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + ...\)
For our function f(x) = ln(1+x), let's calculate the derivatives:
\(f'(x) = \frac{1}{1+x}\\f''(x) = -\frac{1}{(1+x)^2}\\f'''(x) = \frac{2}{(1+x)^3}\\f''''(x) = -\frac{6}{(1+x)^4}\\ ...\)
To find the coefficients in the Maclaurin series, we evaluate the derivatives at x = 0:
f(0) = ln(1+0) = ln(1) = 0
f'(0) = 1
f''(0) = -1
f'''(0) = 2
f''''(0) = -6
...
Now we can substitute these values into the Maclaurin series expansion formula:
\(f(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + ...\)
\(f(x) = 0 + 1x + \frac{-1}{2!}x^2 + \frac{2}{3!}x^3 + ...\)
Simplifying and continuing the pattern:
\(f(x) =x - \frac{1}{2}x^2 + \frac{1}{3}x^3 + ...\)
Therefore, the Maclaurin series expansion for ln(1+x) is:
ln(1+x) \(=x - \frac{1}{2}x^2 + \frac{1}{3}x^3 + ...\)
To learn more about the maclaurin series from the given link
brainly.com/question/30756411
#SPJ4
Lauren has a choice of two health care plans. Option A charges $500 for the year and $65 each time she visits the doctor. Option B charges only $300 for the year but $95 for each doctor's visit. How many visits will she have to make in a year for Option A to be the better deal?
part A Define your variable
part B Write an inequality to represent the situation.
part C Solve the inequality, showing all work in the box below. Write your answer in a complete sentence.
Answers
Answer:
I don't know how to answer all the different parts but Lauren would have to have 6 doctor visits to make Option A the better deal.
Step-by-step explanation:
what is the area of this face

Answers
explanation: 12 x 18 = 216
216 - (6 x 6)
216 - 36 = 180
(a) If you choose a single nucleotide at random from each of the two regions, what is the probability that they are the same nucleotide?
(b)You random sample a three-nucleotide sequence from each of the 2 regions. What is the chance that the triple chosen from the first region will be identical to the triple chosen from the second region? (assume that nucleotides occur independently within each region)
Answers
(a) The probability that a randomly chosen nucleotide from the first region is the same as a randomly chosen nucleotide from the second region is 1/4.
(B) The chance that the triple chosen from the first region will be identical to the triple chosen from the second region is 1/4096.
Nucleotide Probabilities: Single and Triple(a) If we assume that there are four possible nucleotides (A, C, G, T) and that each nucleotide is equally likely to occur in each region, then the probability that a randomly chosen nucleotide from the first region is the same as a randomly chosen nucleotide from the second region is 1/4, since there is a 1 in 4 chance that the nucleotide chosen from the first region will be the same as the nucleotide chosen from the second region.
(b) If we again assume that there are four possible nucleotides (A, C, G, T) and that each nucleotide is equally likely to occur in each region, then the probability of choosing a particular three-nucleotide sequence is (1/4)³ = 1/64.
The probability of choosing the same three-nucleotide sequence from both regions is the product of the probabilities of choosing that sequence from each region, or (1/64) x (1/64) = 1/4096. Therefore, the chance that the triple chosen from the first region will be identical to the triple chosen from the second region is 1/4096.
Learn more about Nucleotide Probabilities: Single and Triple here:
https://brainly.com/question/25161031
#SPJ4
8 students take 18 hours to construct a raft.
If the raft needs to be completed 12 hours earlier, calculate how many more students are needed.
Answers
Answer:
16
Step-by-step explanation:
Students 8 x
Time taken (hours) 18 18 - 12 = 6
If number of students increases, the work will completed in less hours.
So inverse proportion
\(x =\frac{18*8}{6}=3*8 = 24\)
Additional students required = 24 - 8 = 16
the graph of the sales of a new product at a candy store, where x is time in months and y is number sold in hundreds, goes through the points (4, 2) and (6, 8). what is the rate of change, in candies sold per month?
Answers
The rate of change in candies sold per month is 3 hundred candies.
What is the Rate of change?The momentum of a variable is conveyed by the rate of change, which is used for expressing the percentage change in value over a particular amount of time.
To find the rate of change in candies sold per month, it is necessary to find the slope of the line connecting the two points.
The slope formula is given by: Δ\(\frac{y}{x}\)\(\frac{y2-y1}{x2-x1}\)
Using the coordinates of the points, \(\frac{8-2}{6-4} =\frac{6}{2} =3\)
The slope is 3. This means that for every month, the store sells 300 more candies.
Therefore, the rate of change, in candies sold per month is 300.
Learn more about the Rate of change here:
brainly.com/question/8728504
#SPJ11
An individual's per kg expenditure on coffee is distributed with mean $2.32 and variance 0.09 If each individual in the population drinks 3 kg of tea and 2 kg of coffee, the mean total expenditure an beverages is $ with a variance of □, If T and C have a bivariate normal distribution with covariance zero, the mean total expenditure an beverages is $□ with a variance of □. If X and Y have a bivariate distribution with covariance zero, this implies that the variables show
Answers
The mean total expenditure on beverages is $736 with a variance of $8.1912.
If X and Y have a bivariate distribution with covariance zero, this implies that the variables show no linear relationship.
Given that an individual's per kg expenditure on coffee is distributed with mean $2.32 and variance 0.09.
Each individual in the population drinks 3 kg of tea and 2 kg of coffee.
Let T and C be the amount spent on tea and coffee respectively by an individual.
Then,
Total expenditure on coffee = 2 × 2.32 × 100 = $232
and,
Total expenditure on tea = 3 × 1.68 × 100 = $504
We know that the covariance of T and C is zero.
Thus, Mean of the total expenditure on beverages = 232 + 504 = $736,
The variance of the total expenditure on beverages = 4 × variance of expenditure on coffee + 9 × variance of expenditure on tea
= 4 × 0.09 × (2.32)² + 9 × 0.04 × (1.68)²
= $8.1912
Hence, the mean total expenditure on beverages is $736 with a variance of $8.1912.
If X and Y have a bivariate distribution with covariance zero, this implies that the variables show no linear relationship.
To know more about linear relationship visit:
https://brainly.com/question/29066440
#SPJ11
What is the inverse of 3y-12x=-72 in f^-1(x) notation?
Answers
The inverse of the function in \(f^{-1}\) notation is \(f^{-1}=x/4+6\).
What is an inverse function?
An inverse in mathematics is a function that "undoes" another function. In other words, if f(x) produces y, then y entered into the inverse of f produces x. An invertible function is one that has an inverse, and the symbol \(f^{-1}\) represents the inverse.
The output of a function is returned by the inverse function, which also returns the initial value. Consider the inverse relationship between the functions f and g: f(g(x)) = g(f(x)) = x. The initial value is fetched via a function that is its inverse. Therefore, the inverse of f is g(y) = (y-5)/2 = x. (x).
A function 3y-12x=-72 is given.
Switch x for y in the given function.
3x-12y=-72
Solve for y in the given function.
12y=3x+72
y=x/4+6
\(f^{-1}=x/4+6\)
So, the inverse of the function in \(f^{-1}\) notation is \(f^{-1}=x/4+6\).
To know more about the inverse of a function:
https://brainly.com/question/3831584
#SPJ1