Answers
We need to use the concept of Finding zeros of the polynomial function. The zeros of the function are 1/2,1+2i,1-2i.
How do you find the zeros of the polynomial?The values of x that fulfill the formula f(x) = 0 are the zeros of a polynomial. The polynomial's zeros are the x values for which the function's value, f(x), equals zero in this case. The degree of equation f(x) = 0 determines how many zeros a polynomial has. The zeros of the polynomial are all such domain values of the function for which the range is zero.
The locations where the graph of y = f(x) crosses the x-axis are known as the polynomial's zeros graphically. In the information that follows, we will learn more about how to express a polynomial's zeros on a graph.
Calculation:Take f(x)=2x^3 -5x^2+12x-5
So in the question he mentioned that (2x-1) is factor of the polynomial.
So take out (2x-1) from the polynomial function
f(x)=(2x-1)(x^2-2x+5)
We know that zeros of a polynomial can be found when f(x)=0
⇒(2x-1)=0
∴x=1/2
⇒(x^2-2x+5)=0
By using the concept of finding roots of a quadratic equation
(-b±√b2-4ac)/2a
⇒(2±4i)/2
∴x=(1+2i) and (1-2i)
∴1/2,(1+2i),(1-2i) are the zeros.
We need to use the concept of Finding zeros of the polynomial function. The zeros of the function are 1/2,1+2i,1-2i.
To refer more about Finding zeros of the polynomial function, visit:
https://brainly.com/question/18775313
#SPJ1
Related Questions
Two angles form a linear pair. The expression for one angle is x + 18 and the expression for the other is 2x. Find the measure of both angles
Answers
The measure of the first angle is x + 18, and the measure of the second angle is 2x. To find the measure of both angles, we can set up an equation based on the fact that the two angles form a linear pair.
A linear pair consists of two adjacent angles that form a straight line, totaling 180 degrees. In this case, the measure of the first angle is given as x + 18, and the measure of the second angle is given as 2x. To find the values of x and the measures of both angles, we can set up the equation (x + 18) + (2x) = 180, representing the sum of the two angles. Simplifying the equation, we have 3x + 18 = 180. Subtracting 18 from both sides, we get 3x = 162. Dividing by 3, we find x = 54. Substituting the value of x back into the expressions for the angles, the measure of the first angle is 54 + 18 = 72 degrees, and the measure of the second angle is 2 * 54 = 108 degrees. Therefore, the first angle measures 72 degrees, and the second angle measures 108 degrees.
Learn more about angles here:
https://brainly.com/question/31996286
#SPJ11
In response to a gss question in 2006 about the number of hours spent per day watching television, the responses by the fifteen subjects who identified themselves as Buddhist were 0, 0, 0, 1, 1, 1, 2, 2, 2, 2, 2, 3, 4, 4, and 5. For these fifteen subjects, the mean number of hours spent per day watching television is 1.93 hours. What is the standard error of this mean estimate?
Answers
Answer:
Standard error = 0.4
Step-by-step explanation:
Step 1
We find the Standard Deviation
The formula = √(x - mean)/n - 1
n = 15
Mean = 1.93 hours
= √(0- 1.93)² + (0-1.93)² +(0- 1.93)²+( 0- 1.93)²+ (1- 1.93)² + (1- 1.93)² +(1 - 1.93)² +(2 - 1.93)² + (2 - 1.93)² + (2 - 1.93)² + (2 - 1.93)² + ( 2 - 1.93)² +(4 - 1.93)² +(4 - 1.93)² + (5 - 1.93)²/15 - 1
= √(3.737777776 + 3.737777776 + 3.737777776 + 0.871111111 +0.871111111 + 0.871111111 + 0.004444444445+ 0.004444444445 + 0.004444444445 + 0.004444444445 + 0.004444444445 + 1.137777778 + 4.271111112 + 4.271111112 + 9.404444446)/15 - 1
= √2.352380952
= 1.533747356
Step 2
We find the standard error
The formula = Standard Deviation/√n
Standard deviation = 1.533747356
n = 15
= 1.533747356/√15
= 1.533747356 /3.87298334621
= 0.39601186447
Approximately = 0.4
Therefore, the standard error is 0.4
Consider the following vector field.
F(x, y, z) =
9ex sin(y), 2ey sin(z), 8ez
sin(x)
(a)
Find the curl of the vector field.
curl(F) =
(b)
Find the divergence of the vector field.
div(F) =
Answers
The curl of the vector field
curl(F) = -2ey cos(z)i + 8ez cos(x)j - 9ex cos(y)k
The divergence of the vector field
div(F) = 9e^x sin(y) + 2e^y sin(z) + 8e^z
To find the curl of the vector field F(x, y, z) = 9ex sin(y), 2ey sin(z), 8ez sin(x), we need to compute the determinant of the curl matrix.
(a) Curl of F:
The curl of a vector field F = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k is given by the following formula:
curl(F) = (∂R/∂y - ∂Q/∂z)i + (∂P/∂z - ∂R/∂x)j + (∂Q/∂x - ∂P/∂y)k
In this case, we have:
P(x, y, z) = 9ex sin(y)
Q(x, y, z) = 2ey sin(z)
R(x, y, z) = 8ez sin(x)
Taking the partial derivatives, we get:
∂P/∂y = 9ex cos(y)
∂Q/∂z = 2ey cos(z)
∂R/∂x = 8ez cos(x)
∂R/∂y = 0 (no y-dependence in R)
∂Q/∂x = 0 (no x-dependence in Q)
∂P/∂z = 0 (no z-dependence in P)
Substituting these values into the curl formula, we have:
curl(F) = (0 - 2ey cos(z))i + (8ez cos(x) - 0)j + (0 - 9ex cos(y))k
= -2ey cos(z)i + 8ez cos(x)j - 9ex cos(y)k
Therefore, the curl of the vector field F is given by:
curl(F) = -2ey cos(z)i + 8ez cos(x)j - 9ex cos(y)k
(b) Divergence of F:
The divergence of a vector field F = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k is given by the following formula:
div(F) = ∂P/∂x + ∂Q/∂y + ∂R/∂z
In this case, we have:
∂P/∂x = 9e^x sin(y)
∂Q/∂y = 2e^y sin(z)
∂R/∂z = 8e^z
Substituting these values into the divergence formula, we have:
div(F) = 9e^x sin(y) + 2e^y sin(z) + 8e^z
Therefore, the divergence of the vector field F is given by:
div(F) = 9e^x sin(y) + 2e^y sin(z) + 8e^z
Learn more about divergence of the vector this link:
https://brainly.com/question/30907324
#SPJ11
sketch the linear equation 2x+y=35
Answers
Answer: Here, i graphed it on desmos

Answer:
Step-by-step explanation:
You want to get the Y alone so what you would do is move the 2x on the others side of the equation which changes the sign to a negative and now it should look like this: y=-2x+35. Then you sketch it on a graph. Hopes this helped!
Simplify the expression by
distributing, then combining like
terms!
4 (3x + 2) - 6
Answers
Answer:
\(\boxed {12x + 2}\)
Step-by-step explanation:
Solve the following expression:
\(4(3x + 2) - 6\)
-Use Distributive Property:
\(4(3x + 2) - 6\)
\(12x + 8 - 6\)
-Combine like terms:
\(12x + 8 - 6\)
\(\boxed {12x + 2}\)
Answer:
\(12x+2\)
Step-by-step explanation:
The first step is to distribute the 4 to the parenthesis. This turns the equation into:
\((12x+8)-6\)
We can remove the parenthesis now. Also, now we combine like terms. There are no other variables in the equation, so we leave the 12x alone. Combine the +8 and the -6 to get +2. This leaves the equation at:
\(12x+2\)
Solve the System of Linear Equations by
Substitution with work
3x - 4y = 19
x=5
Answers
15-4y=19
subtract 15 from both sides
-4y = 19
divide both sides by -4
y = -1
i think thats what u were trying to ask if not reply back
Triangle SAM is congruent to Triangle REN. Find x and y.

Answers
\(\measuredangle A\cong \measuredangle E\implies 112=16x\implies \cfrac{112}{16}=x\implies \boxed{7=x} \\\\[-0.35em] ~\dotfill\\\\ \overline{MS}\cong \overline{NR}\implies 41=3x+5y\implies 41=3(7)+5y\implies 41=21+5y \\\\\\ 20=5y\implies \cfrac{20}{5}=y\implies \boxed{4=y}\)
two gears, A and B. are arranged so that the teeth of one gear is mesh with the teeth of another. Gear A turns clockwise and has 54 teeth. Gear B turns counterclockwise and has 36 teeth. If gear A makes 5.5 rotations, how many turns will gear B make?
Answers
The number of turns gear B will make is 8.25 turns
How to find the number of turns gear B will makeGiven data
Gear A turns clockwise and has 54 teeth
Gear B turns counterclockwise and has 36 teeth
gear A makes 5.5 rotations
One of the gears is driving the other hence the distance covered by each of the gears is constant.
The distance is the product of the number of rotations and the number of teeth and this should be a constant
Therefore, let the number of rotations of gear B be x
54 teeth * 5.5 rotations = 36 teeth * x rotations
x rotations = ( 54 teeth * 5.5 rotations ) / 36 teeth
x rotations = 54/36 * 5.5
x rotations = 1.5 * 5.5
x rotations = 8.25
We can therefore say that gear B will make 8.25 rotations
Read more on rotation calculations here: https://brainly.com/question/13286537
#SPJ1
A tank at an oil refinery is to be coated with an industrial strength coating. The surface area of the tank is 80,000 square feet. The coating comes in five-gallon buckets. The area that the coating in one randomly selected bucket can cover, varies with mean 2000 square feet and standard deviation 100 square feet.
Calculate the probability that 40 randomly selected buckets will provide enough coating to cover the tank. (If it matters, you may assume that the selection of any given bucket is independent of the selection of any and all other buckets.)
Round your answer to the fourth decimal place.
Answers
The probability that 40 randomly selected buckets will provide enough coating to cover the tank is 0.5000 or 0.5000 (approx) or 0.5000
Given: The surface area of the tank is 80,000 square feet. The coating comes in five-gallon buckets. The area that the coating in one randomly selected bucket can cover varies, with a mean of 2000 square feet and a standard deviation of 100 square feet.
The probability that 40 randomly selected buckets will provide enough coating to cover the tank. (If it matters, you may assume that the selection of any given bucket is independent of the selection of any and all other buckets.)
The area covered by one bucket follows a normal distribution, with a mean of 2000 and a standard deviation of 100. So, the area covered by 40 buckets will follow a normal distribution with a mean μ = 2000 × 40 = 80,000 and a standard deviation σ = √(40 × 100) = 200.
The probability of the coating provided by 40 randomly selected buckets will be enough to cover the tank: P(Area covered by 40 buckets ≥ 80,000).
Z = (80,000 - 80,000) / 200 = 0.
P(Z > 0) = 0.5000 (using the standard normal table).
Therefore, the probability that 40 randomly selected buckets will provide enough coating to cover the tank is 0.5000 or 0.5000 (approx) or 0.5000 (rounded to four decimal places).
Learn more about Probability calculation in coating coverage:
brainly.com/question/17400210
#SPJ11
help me I need help on this

Answers
Answer:
It is 1.
Step-by-step explanation:
Hope this helped have an amazing day!
a surveyor took some measurements of a piece of land. the owner needs to know the area of the land to determine the value. what is the area of the piece of land?
Answers
The area of the piece of land is 849 ft².
The area of the piece of land
=22 x 30 x \(\frac{1}{2}\) x 2 + (30-12) x 21 x \(\frac{1}{2}\)
=660 + 18 × 21×\(\frac{1}{2}\)
=660 + 189
=849 ft²
The area is the amount that expresses the volume of a place on the plane or on a curved surface. The location of an aircraft region or aircraft place refers back to the area of a shape or planar lamina, at the same time as floor region refers to the location of an open floor or the boundary of a three-dimensional object. the area may be understood as the amount of fabric with a given thickness that could be essential to style a model of the shape, or the amount of paint vital to cowl the surface with a single coat. it's miles the 2-dimensional analog of the length of a curve (a one-dimensional concept) or the extent of a strong (a three-dimensional concept).
The place of a shape can be measured by way of evaluating the form to squares of a hard and fast size. inside the global gadget of devices (SI), the usual unit of the vicinity is the rectangular meter (written as m²), that's the location of a rectangle whose sides are one meter long. A shape with a place of three rectangular meters would have the equal region as 3 such squares. In mathematics, the unit square is described to have placed one, and the location of another shape or floor is a dimensionless real variety.
To learn more about the Area visit here:
brainly.com/question/28770672
#SPJ4
six new employees, two of whom are married to each other, are to be assigned six desks that are lined up in a row. if the assignment of employees to desks is made at randomly, what is the probability that the married couple will not have adjacent desks?
Answers
The total number of ways to assign employees to desks is 720 (6!), and the number of favorable outcomes is 144. Therefore, the probability is 144/720 = 1/5.
The total number of ways to assign six employees to six desks is 6! (6 factorial), which equals 720. Now we need to find the number of ways that the married couple will not have adjacent desks.
First, we can treat the married couple as one entity, which means we have 5 entities to assign to 6 desks. There are 6 possible ways to choose the position of the married couple in the row. For each of these positions, we can then assign the other 4 entities to the remaining 4 desks in 4! ways.
Therefore, the total number of ways to assign employees to desks without the married couple having adjacent desks is 6 x 4! = 144.
The probability of this happening is the number of favorable outcomes (144) divided by the total number of possible outcomes (720), which is 144/720 = 1/5.
The probability that the married couple will not have adjacent desks when six new employees are randomly assigned to six desks that are lined up in a row is 1/5.
We calculated this probability by first treating the married couple as one entity and then finding the number of ways to assign the remaining entities to the desks without the married couple being adjacent to each other. The total number of ways to assign employees to desks is 720 (6!), and the number of favorable outcomes is 144. Therefore, the probability is 144/720 = 1/5.
To know more about probability visit:
brainly.com/question/32004014
#SPJ11
Select the car that travels the fastest. choose 1 answer: choose 1 answer: (choice a, checked) a 50 50 km/h km/hcar a (choice b) b car b travels a distance of d dd kilometers in h hh hours, based on the equation 55 h = d 55h=d55, h, equals, d. (choice c) c car c travels 135 135135 kilometers in 3 33 hours. see more
Answers
The car with the speed of 50 Km/h travels the fastest.
We have given with three choices for selecting the fastest speed from them. The three choices are
First choice is 50 Km/h.
Second Choice is car b travels a distance of d kilometers in h hours, based on the equation 55 h = d , h, equals, d.. So from this be can conclude that this car is moving with the speed of (1/55)km/h.
Third choice is car c travels 135 kilometers in 3 hours. So from this be can conclude that this car is moving with the speed of (135/3) Km/h i.e., 45 Km/h.
So, from the given choices we can conclude that the car with the speed of 50 Km/h travels the fastest.
To know more about Speed refer to the link:
https://brainly.com/question/13943409
#SPJ4
The ages of 2 persons differs by 20 years
5 years ago. The elder one was 5 times as old
as the Younger one, what is their present ages?
years?
Answers
Answer:
Let their ages be x and (x + 20) years.
5 (x - 5) = (x + 20 - 5) or 4x = 40 or x = 10.
Their present ages are 30 years and 10 years.
Mai drew the design shown below. Each
rectangle in the design has the same
area. Each rectangle is what fraction of
the area of the complete design?
Answers
Each rectangle is 1/3 of the area of the complete design.
What fraction of the area of the complete design?A fraction represents the parts of a whole or collection of objects e.g. 3/4 shows that out of 4 equal parts, we are referring to 3 parts.
Looking at the design, you will be notice that the main (bigger) rectangle is divided to three smaller rectangles. Thus, each rectangle is one out of three rectangles i.e. 1/3.
Therefore, each rectangle is 1/3 of the area of the complete design.
Learn more about fraction on:
brainly.com/question/11562149
#SPJ1
Complete Question
Check attached image

-10 plus -9 ??????????
Answers
Answer: -19
Step-by-step explanation:
(-10) + (-9)
-10-9
-19
I WILL GIVE BRAINLIEST PLS HURRY A student is saving money to go on a school field trip. The graph shows the relationship between the number of weeks the student has been saving, x, and the total dollar amount they have saved, y.
coordinate plane with the x axis labeled number of weeks and the y axis labeled total savings in dollars, with a line that passes through the points 0 comma 20 and 5 comma 40
Determine the slope and explain its meaning in terms of the real-world scenario.
A: The slope is one fourth, which means that the student's total savings increases by $0.25 each week.
B: The slope is 4, which means that the student's total savings increases by $4 each week.
C: The slope is 12, which means that the student will finish saving money after 12 weeks.
D: The slope is 20, which means that the student started with $20.

Answers
The slope in this scenario is explained as: "B. The slope is 4, which means that the student's total savings increases by $4 each week."
How to Determine and Interpret the Slope of a Scenario?The slope is also the unit rate which is the ratio of the change in y over the change in x for a given scenario.
The slope of the graph shown would be the total savings increase in dollars per week that is made by the student.
using two points on the graph, (0, 20) and (5, 40), we have:
Slope (m) = 40 - 20 / 5 - 0
Slope (m) = 4
Therefore, the answer is: "B. The slope is 4, which means that the student's total savings increases by $4 each week."
Learn more about the slope on:
https://brainly.com/question/29277016
#SPJ1
Use a table to show the sample space of two-digit numbers using the digits 1,4,5,9. Use the column label as the tens digit and the row label as the ones digit to complete the table that represents the sample space of two-digit numbers.
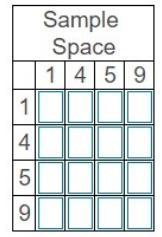
Answers
Answer:
19
Step-by-step explanation:
!!!!!!
The pair of points lies on the same line with the given slope. Find x.
(5,8). (x,14); slope = 2
Find x.
(Type an integer or a simplified fraction.)
Answers
Answer:
required Value of x is x=8
Step-by-step explanation:
We are given two points: (5,8) and (x,14) and slope =2 . We need to find value of x.
The formula used to find slope is: \(Slope=\frac{y_2-y_1}{x_2-x_1}\)
We are given slope =2 , x₁=5, y₁=8, x₂=x, y₂=14
So, we actually need to find value of x₂. Putting values in formula and find value of x
\(Slope=\frac{y_2-y_1}{x_2-x_1}\\2=\frac{14-8}{x-5}\\Solving:\\2(x-5)=6\\2x-10=6\\2x=6+10\\2x=16\\x=\frac{16}{2}\\x=8\)
So, required value of x=8
Determine f –1(x) if f of x is equal to the quantity x plus 2 end quantity over the quantity x minus 3 end quantity where x ≠ 3.
f inverse of x is equal to the quantity x minus 3 end quantity over the quantity x plus 2 end quantity
b
f inverse of x is equal to the quantity x minus 2 end quantity over the quantity x plus 3 end quantity
c
f inverse of x is equal to the quantity x minus 1 end quantity over the quantity 3 times x plus 2 end quantity
d
f inverse of x is equal to the quantity 3 times x plus 2 end quantity over the quantity x minus 1 end quantity
Answers
The inverse function of f(x) = (x + 2)/(x - 3) is given as follows:
\(f^{-1}(x) = \frac{3x + 2}{x - 1}\)
How to obtain the inverse function?The function in this problem is defined as follows:
f(x) = (x + 2)/(x - 3).
Using the notation y = f(x), it is given as follows:
y = (x + 2)/(x - 3).
To obtain the inverse, the first step is exchanging the variables x and y, as follows:
x = (y + 2)/(y - 3).
Now the variable y must be isolated to obtain the inverse function, as follows:
xy - 3x = y + 2
xy - y = 3x + 2
y(x - 1) = 3x + 2
y = (3x + 2)/(x - 1).
Hence the inverse function is given by:
\(f^{-1}(x) = \frac{3x + 2}{x - 1}\)
Meaning that the fourth option is correct.
More can be learned about inverse functions at brainly.com/question/3831584
#SPJ1
Average movie prices in the United States are, in general, lower than in other countries. It would cost $79. 91 to buy three tickets in Japan plus two tickets in Switzerland. Three tickets in Switzerland plus two tickets in Japan would cost $75. 59. How much does an average movie ticket cost in each of these countries
Answers
The average cost of a movie ticket in Japan is $17.71, while in Switzerland, it is $13.39,
Let's assume the average cost of a movie ticket in Japan is denoted by "J" and the average cost of a movie ticket in Switzerland is denoted by "S".
According to the given information, we can set up the following equations:
3J + 2S = $79.91 (equation 1)
3S + 2J = $75.59 (equation 2)
To solve this system of equations, we can use a method called substitution. We can solve equation 1 for J and substitute it into equation 2:
From equation 1, we can isolate J:
3J = $79.91 - 2S
J = ($79.91 - 2S)/3
Substituting J into equation 2:
3S + 2(($79.91 - 2S)/3) = $75.59
Now we can solve for S:
3S + (2($79.91 - 2S))/3 = $75.59
Multiplying through by 3 to clear the fraction:
9S + 2($79.91 - 2S) = $226.77
Distributing:
9S + $159.82 - 4S = $226.77
Combining like terms:
5S + $159.82 = $226.77
Subtracting $159.82 from both sides:
5S = $66.95
Dividing by 5:
S = $13.39
Now that we know the cost of a movie ticket in Switzerland is $13.39, we can substitute this value back into equation 1 to find the cost of a movie ticket in Japan:
3J + 2($13.39) = $79.91
3J + $26.78 = $79.91
3J = $53.13
Dividing by 3:
J = $17.71
Therefore, the average movie ticket cost in Japan is $17.71, and in Switzerland, it is $13.39.
learn more about average cost here:
https://brainly.com/question/29073158
#SPJ11
find the gradient of the line 3y=2x/3+4
Answers
Answer:
slope is also known as gradient
here gradient =2/9
On a math quiz, Tatiana earns 5 points for each question she answers correctly. She wrote this
equation to find how many points she earns (p) based on how many questions she answers
correctly (g):
p = 5q
Identify the dependent and independent variables.
Points earned (p)
Questions correct (g)
Dependent variable Independent variable

Answers
Answer:
For points earned (p), the button should be on the left, and for questions correct (q), its on the right.
Step-by-step explanation:
me not know how to speak English!
In the given equation p = 5q, p is the dependent variable and g is the independent variable.
Given that Tatiana earns 5 points for each question she answers.
So, the equation is p = 5q
The above equation explains that for every question she answers, she earns 5 points. That means answering questions which is "q" is an independent variable as it is not depending on any other factor.
The points earned which is "p", is completely depending on answering questions, so the "p" which is points earned is a dependent variable.
From the above explanation, we can conclude that p is dependent variable and q is independent variable.
To know more about the dependent variables,
https://brainly.com/question/25223322
#SPJ1
Which point would I use in the equation? Don’t answer the question in the picture.

Answers
Given:
The coordinates of line are, (-3,2) and (1,10).
The objective is to choose the correct equation of line.
Explanation:
Consider the given coordinates as,
\(\begin{gathered} (x_1,y_1)=(1,10) \\ (x_2,y_2)=(-3,2) \end{gathered}\)The general formula to find the equation of line using two points is,
\(y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\)On plugging the coordinates in the above equation.
\(\begin{gathered} y-10=\frac{2-10}{-3-1}(x-1) \\ y-10=\frac{-8}{-4}(x-1) \\ y-10=2(x-1) \end{gathered}\)Thus, the equation of the line obtained is y - 10 = 2(x - 1).
Hence, option (A) is the correct answer.
Solve the quadratic by taking square roots Round to the nearest tenth. 2x² - 9 = 121
Answers
Answer:
x ≈ ±8.1
Step-by-step explanation:
2x² -9 = 121 . . . . given
2x² = 130 . . . . . . add 9
x² = 65 . . . . . . . .divide by 2
x = ±√65 . . . . . take the square root
x ≈ ±8.1
Choose the inequality that represents the following graph.

Answers
Answer:
D) x ≥ -2
Step-by-step explanation:
ay - b = c solve for y
Answers
Answer:
\(Y=\frac{c}{a}-\frac{b}{a}\)
Step-by-step explanation:
Answer:
y=c+b/a (The a is under c+b)
Step-by-step explanation:
Add the b over to c.
ay=c+b
Now divide both sides by a, which will remove the a from y.
y=c+b/a
11. While on vacation, Santiago wants to go snorkeling.
Coral Snorkeling charges $25 to rent equipment and
$30 per hour of boat rental. Sea Water Adventures'
costs are shown in the graph. Santiago wants
to snorkel for 3 hours. Which company costs less
for 3 hours? How much less?
Answers
Answer:
both cost the same amount of money
Step-by-step explanation:
The answer what is it
Answers
Assume there is a sample of n
1
=4, with the sample mean
X
1
=35 and a sample standard deviation of S
1
=4, and there is an independent sample of n
2
=5 from another population with a sample mean of
X
ˉ
2
=31 and a sample standard deviation S
2
=5. In performing the pooled-variance t test, how many degrees of freedom are there? There are degrees of freedom. (Simplify your answer.)
Answers
There are 7 degrees of freedom.
In performing the pooled-variance t test, the degrees of freedom can be calculated using the formula:
df = (n1 - 1) + (n2 - 1)
Substituting the given values:
df = (4 - 1) + (5 - 1)
df = 3 + 4
df = 7
Therefore, there are 7 degrees of freedom.
Learn more about degrees of freedom
brainly.com/question/32093315
#SPJ11
There are 7 degrees of freedom for the pooled-variance t-test.
To perform a pooled-variance t-test, we need to calculate the degrees of freedom. The formula for degrees of freedom in a pooled-variance t-test is:
\(\[\text{{df}} = n_1 + n_2 - 2\]\)
where \(\(n_1\)\) and \(\(n_2\)\) are the sample sizes of the two independent samples.
In this case, \(\(n_1 = 4\)\) and \(\(n_2 = 5\)\). Substituting these values into the formula, we get:
\(\[\text{{df}} = 4 + 5 - 2 = 7\]\)
In a pooled-variance t-test, we combine the sample variances from two independent samples to estimate the population variance. The degrees of freedom for this test are calculated using the formula \(df = n1 + n2 - 2\), where \(n_1\)and \(n_2\) are the sample sizes of the two independent samples.
To understand why the formula is \(df = n1 + n2 - 2\), we need to consider the concept of degrees of freedom. Degrees of freedom represent the number of independent pieces of information available to estimate a parameter. In the case of a pooled-variance t-test, we subtract 2 from the total sample sizes because we use two sample means to estimate the population means, thereby reducing the degrees of freedom by 2.
In this specific case, the sample sizes are \(n1 = 4\) and \(n2 = 5\). Plugging these values into the formula gives us \(df = 4 + 5 - 2 = 7\). Hence, there are 7 degrees of freedom for the pooled-variance t-test.
Therefore, there are 7 degrees of freedom for the pooled-variance t-test.
Learn more about t-test
https://brainly.com/question/13800886
#SPJ11
