Answers
Answer: The value of P is 38 at (7,2)
Related Questions
Select all statements below which are true for all invertible × matrices and = B. 4 is invertible C. (+)^2=^2+^2+2 D. + is invertible E. (+−1)^9=^9+^−9 F. (−)(+)=−^2
Answers
Answer:
hello your question is poorly written below is the well written question and the options aren't available hence i will provide a general answer
Select all statements below which are true for all invertible n × n matrices. A and B
answer : a)(In+A)(In+A^-1) = In + A^-1 +A +AA^-1 = In + A^-1 +A + In = 2In+A+A^-1.
since (AB)^-1 = B^-1 *A^-1 hence
b) (A^6)^-1 will be (AAAAAA)^-1= (A^-1)( A^-1)( A^-1)( A^-1)( A^-1)( A^-1) = (A-1)6.
Step-by-step explanation:
The True statements for all invertible n x n matrices A and B are :
(In+A)(In+A^-1) = In + A^-1 +A +AA^-1 = In + A^-1 +A + In = 2In+A+A^-1.
since (AB)^-1 = B^-1 *A^-1 hence (A^6)^-1 will be (AAAAAA)^-1= (A^-1)( A^-1)( A^-1)( A^-1)( A^-1)( A^-1) = (A-1)6.
Solve the equation by dividing. 125 = 5f
Answers
Answer:
Answer = 25
Step-by-step explanation:
125 = 5f
125/5 = f
25 = f
125/5=f
f=25
Here is the answer for this question
Solve Triangle
Because I Need Answer My Assignment:-)
Good Perfect Complete=Brainlist
Copy Wrong Incomplete=Report
Good Luck Answer Brainly Users:-)

Answers
Answer:
x = 4√5 ≈ 8.94 (2 d.p.)
y = 8√5 ≈ 17.89 (2 d.p.)
Step-by-step explanation:
To find the values of x and y, use the Geometric Mean Theorem (Leg Rule).
Geometric Mean Theorem (Leg Rule)The altitude drawn from the vertex of the right angle perpendicular to the hypotenuse separates the hypotenuse into two segments. The ratio of the hypotenuse to one leg is equal to the ratio of the same leg and the segment directly opposite the leg.
\(\boxed{\sf \dfrac{Hypotenuse}{Leg\:1}=\dfrac{Leg\:1}{Segment\;1}}\quad \sf and \quad \boxed{\sf \dfrac{Hypotenuse}{Leg\:2}=\dfrac{Leg\:2}{Segment\;2}}\)
From inspection of the given right triangle RST:
Altitude = SVHypotenuse = RT = 20Leg 1 = RS = ySegment 1 = RV = 16Leg 2 = ST = xSegment 2 = VT = 4Substitute the values into the formulas:
\(\boxed{\dfrac{20}{y}=\dfrac{y}{16}}\quad \sf and \quad \boxed{\dfrac{20}{x}=\dfrac{x}{4}}\)
Solve the equation for x:
\(\implies \dfrac{20}{x}=\dfrac{x}{4}\)
\(\implies 4x \cdot \dfrac{20}{x}=4x \cdot \dfrac{x}{4}\)
\(\implies 80=x^2\)
\(\implies \sqrt{x^2}=\sqrt{80}\)
\(\implies x=\sqrt{80}\)
\(\implies x=\sqrt{4^2\cdot 5}\)
\(\implies x=\sqrt{4^2}\sqrt{5}\)
\(\implies x=4\sqrt{5}\)
Solve the equation for y:
\(\implies \dfrac{20}{y}=\dfrac{y}{16}\)
\(\implies 16y \cdot \dfrac{20}{y}=16y \cdot \dfrac{y}{16}\)
\(\implies 320=y^2\)
\(\implies \sqrt{y^2}=\sqrt{320}\)
\(\implies y=\sqrt{320}\)
\(\implies y=\sqrt{8^2\cdot 5}\)
\(\implies y=\sqrt{8^2}\sqrt{5}\)
\(\implies y=8\sqrt{5}\)


The graph of the function f ( x ) is shown

Answers
The true statements for the given function f(x) are:
The value of g(1) is 3 and the y- intercept of g(x) is at the point (0, 1) .
How to calculate the values of the function?The function g(x) = f( x - 3 )
g (1) = f (1 -3 )
= f (-2 )
= 3
g (-1) = f (-1 -3)
= f (-4)
= - 1
Substituting , x = 0 to find the y intercept of g(x)
g ( 0 ) = f ( 0 - 3)
=f (-3)
=1
The y intercept of g(x) is at the point (0, 1)
Thus, options 1 and 4 are the true statements for the given function.
What are functions?Function is a mathematical phrase, rule, or law that establishes the relationship between an independent variable and a dependent variable.In science, engineering, and the majority of the mathematical disciplines, functions are often utilized.Functions are reportedly the central objects of inquiry in the majority of mathematical disciplines. Although some authors establish a distinction between maps and functions, functions are also referred to as maps or mappings.To learn more about functions, refer:
https://brainly.com/question/25638609
#SPJ1
Given circle Q with a measure of SR=120° and a radius of 9 feet, as shown below.
Determine the arc length of SR Use mathematics to explain how you determined your answer.
Help

Answers
Answer:
18.85 feet
Step-by-step explanation:
Determine the arc length of SR
Arc length = θ/360 × 2πr
r = 9 feet
θ =120°
Arc length = 120/360 × 2 × π × 9
= 18.849555922 feet
Approximately = 18.85 feet
Therefore, the arc length of SR = 18.85 feet
PLEASE HELP ME WITH THIS QUESTION, ILL BRAINLIEST YOU
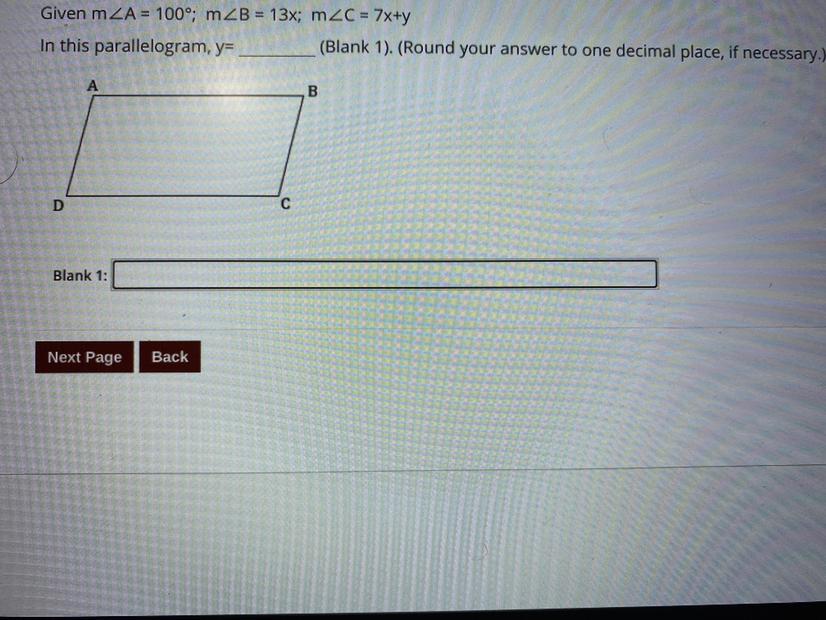
Answers
Answer:
y = 56.9
Step-by-step explanation:
100 + 13x = 180
13x = 80
x= 80/13
7(80/13) + y = 100
y = 56.9
199852 ÷ 98852 × 36578
Answers
Answer:
73950.81997
Step-by-step explanation:
The rounded amount is 73951. Make sure you put the rounded symbol and the one on top as well just in case. (put both answers.)
If angle S and angle T are complementary, and angle T and angle U are supplementary, then angle U is a(n) _________ angle
Answers
Answer:
Obtuse angle
Step-by-step explanation:
S and T are complementary. So, S and T are less than 90°.
T and U are supplementary. So, sum of T and U is 180°.
Since, T is less than 90°, U must be greater than 90°. Hence angle U is an obtuse angle.
Janelys has a points card for a movie theater. She receives 20 rewards points just for signing up. She earns 12.5 points for each visit to the movie theater. She needs at least 165 points for a free movie ticket.
Answers
The inequality shows that the number of visits that Janelys needs at least 165 points for a free movie ticket is 12.
How to calculate the number of visits?From the information, Janelys has a points card for a movie theater and she receives 20 rewards points just for signing up and earns 12.5 points for each visit to the movie theater.
The number of visits that are needed to earn at least 165 points will be illustrated as x. This will be:
20 + 12.5x >= 165
Collect like terms
12.5x >= 165 - 20
12.5x >= 145
Divide
x >= 145 / 12.5
x >= 11.6
Therefore, she needs at least 12 visits.
Learn more about inequalities on;
brainly.com/question/24372553
#SPJ1
Janelys has a points card for a movie theater. She receives 20 rewards points just for signing up. She earns 12.5 points for each visit to the movie theater. She needs at least 165 points for a free movie ticket. How may visits are needed?
Jessica completed 20 haircuts in 8 hours. On average how many haircuts per hour did Jessica do?
Answers
Answer:
two and a half
Step-by-step explanation:
f(x)=x² + 2x - 4; Find ƒ(−1)
Answers
Answer:
f(- 1) = - 5
Step-by-step explanation:
substitute x = - 1 into f(x)
f(x) = x² + 2x - 4 , then
f(- 1) = (- 1)² + 2(- 1) - 4 = 1 - 2 - 4 = - 5
18 is equal to one half of a number
Answers
Answer:
the number is 36 because its half
I’m sorry if it’s wrong
how many times can 3 go into 274.625?
Answers
Answer: About 91.54 times.
Step-by-step explanation:
The number of milligrams D (ht) of a certain drug that is in a patient's bloodstream h hours after the drug is injected is given by the following function.
D(h) = 25e -0. 4
When the number of milligrams reaches 6, the drug is to be injected again. How much time is needed between injections?
Round your answer to the nearest tenth, and do not round any intermediate computations.
Answers
The time is needed between injections is 3.6 hours, i.e., the drug is to be injected again when the number of milligrams reaches 6 mg.
We have the exponential function of number of milligrams D (ht) of a certain drug that is in a patient's bloodstream h hours after the drug is injected is
\(D(h)=25 {e}^{ - 0.4 h}\)
We have to solve for h (the numbers of hours) that would have passed when the D(h) (the amount of medication in the patient's bloodstream) equals 6 mg in order to know when the patient needs to be injected again.
\(6 = 25 {e}^{ - 0.4h} \)
\( \frac{6}{25} = \frac{25}{25} {e}^{ - 0.4h} \)
\(0.24= {e}^{ - 0.4h} \)
Taking logarithm both sides of above equation , we get,
\( \ln(0.24) = \ln( {e}^{ - 0.4h)} \)
Using the properties of natural logarithm,
\( \ln(0.24) = - 0.4h\)
\( - 1.427116356 = - 0.4h\)
\(h = \frac{1.42711635}{0.4} = 3.56779089\)
=> h = 3. 6
So, after 3.6 hours, the patient needs to be injected again.
To learn more about exponential function, refer:
https://brainly.com/question/2456547
#SPJ4
SOMEONE HELP FAST PLEASE.

Answers
Answer:
f(0) = g(0)
Step-by-step explanation:
The functions intersect at x =0, which means they have the same y value at x=0
f(0) = g(0)
Given r = 1-3 sin 0, find the following. Find the area of the inner loop of the given polar curve rounded to 4 decimal places.
Answers
Given r = 1-3 sin 0, find the following. The area of the inner loop of the given polar curve, rounded to four decimal places, is approximately -5.4978.
To find the area of the inner loop of the polar curve r = 1 - 3sin(θ), we need to determine the limits of integration for θ that correspond to the inner loop
First, let's plot the curve to visualize its shape. The equation r = 1 - 3sin(θ) represents a cardioid, a heart-shaped curve.
The cardioid has an inner loop when the value of sin(θ) is negative. In the given equation, sin(θ) is negative when θ is in the range (π, 2π).
To find the area of the inner loop, we integrate the area element dA = (1/2)r² dθ over the range (π, 2π):
A = ∫[π, 2π] (1/2)(1 - 3sin(θ))² dθ.
Expanding and simplifying the expression inside the integral:
A = ∫[π, 2π] (1/2)(1 - 6sin(θ) + 9sin²(θ)) dθ
= (1/2) ∫[π, 2π] (1 - 6sin(θ) + 9sin²(θ)) dθ.
To solve this integral, we can expand and evaluate each term separately:
A = (1/2) (∫[π, 2π] dθ - 6∫[π, 2π] sin(θ) dθ + 9∫[π, 2π] sin²(θ) dθ).
The first integral ∫[π, 2π] dθ represents the difference in the angle values, which is 2π - π = π.
The second integral ∫[π, 2π] sin(θ) dθ evaluates to zero since sin(θ) is an odd function over the interval [π, 2π].
For the third integral ∫[π, 2π] sin²(θ) dθ, we can use the trigonometric identity sin²(θ) = (1 - cos(2θ))/2:
A = (1/2)(π - 9/2 ∫[π, 2π] (1 - cos(2θ)) dθ)
= (1/2)(π - 9/2 (∫[π, 2π] dθ - ∫[π, 2π] cos(2θ) dθ)).
Again, the first integral ∫[π, 2π] dθ evaluates to π.
For the second integral ∫[π, 2π] cos(2θ) dθ, we use the property of cosine function over the interval [π, 2π]:
A = (1/2)(π - 9/2 (π - 0))
= (1/2)(π - 9π/2)
= (1/2)(-7π/2)
= -7π/4.
The area of the inner loop of the given polar curve, rounded to four decimal places, is approximately -5.4978.bIt's important to note that the negative sign arises because the area is bounded below the x-axis, and we take the absolute value to obtain the magnitude of the area.
Learn more about limits of integration here:
https://brainly.com/question/31994684
#SPJ11
Charles uses a graphing calculator to find a quadratic regression model f for a given set of data. When he compares model f to an earlier regression model g for the same data, he determines that g more accurately models the data. Which of the following statements are true? Select all that apply.
A. Function f likely had fewer residuals near the x-axis than function g.
B. Function f likely had more residuals equal to 0 than function g.
C. Function g had more residuals near the y-axis than function f.
Answers
Function f likely had more residuals near the y-axis than function g
What is the residual of a regression equation?A residual is the difference between the observed y-value (from scatter plot) and the predicted y-value (from regression equation line). It is the vertical distance from the actual plotted point to the point on the regression line.
Given here function g plots the model more accurately than function f thus this can only be when function f has more residuals because g plots the model more accurately.
Hence, Function f likely had more residuals near the y-axis than function g
Learn more about regression equation here:
https://brainly.com/question/14184702
#SPJ2
NEED HELP ASAP. Can you also graph the line:
Graph the line that contains the point (-4,-2) and has a slope of 3/4
Answers
Answer:
y= (3/4)x +1
Step-by-step explanation:
Kathy measured her finger using a ruler with centimeters. Then she measured the same finger with a ruler using millimeters. Can Kathy compare the two measurements? Yes, 10 centimeters is the same as 1 millimeter. Yes, 10 millimeters is the same as 1 centimeter. Yes, 1 centimeter is the same as 1 millimeter. No, the student cannot compare them.
Answers
Answer:
Yes, 10 millimeters is the same as 1 centimeter.
Step-by-step explanation:
Kathy can compare the two measurement because 10 millimeters equals 1 centimeter
This means
10 millimeters of her finger = 1 centimeter of the same finger
100 millimeters of her finger = 10 centimeters of her finger
1000 millimeters of her finger = 100 centimeters of her finger
Therefore, Kathy can compare both measurement ( millimeters and centimeters).
Answer:
Yes, 10 millimeters is the same as 1 centimeter.
Step-by-step explanation:
social security and medicare taxes at 6.2 persent and 1.45 percent
for 65000
Answers
Answer:
Please provide a question to be answered.
what is −1.64 as a mixed number in simplest form.
Answers
Answer:
\(-1\dfrac{16}{25}\)
Step-by-step explanation:
\(-1.64 = \dfrac{-164}{100}\)
Strike with 4th table
\(= \dfrac{-41}{25}= -1\dfrac{16}{25}\)
Given the first three terms of a linear sequence: 3x – 2;x+9; 2x + 5 Determine the value of x.
Answers
Answer:
x = 5
Step-by-step explanation:
The difference between consecutive terms will be equal , then
a₂ - a₁ = a₃ - a₂ , that is
x + 9 - (3x - 2) = 2x + 5 - (x + 9) ← distribute parenthesis on both sides
x + 9 - 3x + 2 = 2x + 5 - x - 9 , simplify both sides
- 2x + 11 = x - 4 ( subtract x from both sides )
- 3x + 11 = - 4 ( subtract 11 from both sides )
- 3x = - 15 ( divide both sides by - 3 )
x = 5
Answer:
x = 5
Step-by-step explanation:
Each new term is 1 greater than the previous term. Therefore:
x + 9 = (3x - 2) + 1 Equivalent to x + 9 = 3x - 2 + 1, or:
9 + 2 - 1 = 2x, or 2x = 10
Thus, x = 5
Check by substituting 5 for x as indicated:
3x - 2 becomes 13 (which means the next term must be 14)
x + 9 becomes 14, and
2x + 5 becomes 15
and these consecutive sequence terms are {13, 14, 15}
(For 160,000 it takes 18ms to sort each half. Then merging together the two sorted halves with 80,000 numbers in each of them takes 40-218 = 4 ms. For 320,000 elements, it will take 240 to sort each half and 24 to merge the sorted halves with 160,000 numbers in each, for the total of 240+8 = 88 ms.)
Answers
For a larger input size of 320,000 elements, it will take 240 ms to sort each half and 24 ms to merge the sorted halves, resulting in a total time of 264 ms.
The given information describes the time required for sorting and merging operations on two different input sizes. For 80,000 elements, it takes 18 ms to sort each half, resulting in a total of 36 ms for sorting. Merging the two sorted halves with 80,000 numbers in each takes 40 - 18 = 22 ms.
When the input size is doubled to 320,000 elements, the sorting time for each half increases to 240 ms, as it scales linearly with the input size. The merging time, however, remains constant at 4 ms since the size of the sorted halves being merged is the same.
Thus, the total time for sorting and merging 320,000 elements is the sum of the sorting time (240 ms) and the merging time (4 ms), resulting in a total of 264 ms.
Therefore, based on the given information, the total time required for sorting and merging 320,000 elements is 264 ms.
Learn more about total time here:
https://brainly.com/question/951637
#SPJ11
A soccer game is m minutes long. The game includes 90 minutes plus x minutes of time-outs. Translate the words into an algebraic expression. How long is the game with 8 minutes of time-outs
Answers
The game with 8 minutes of time-outs is 98 minutes long.
What is an algebraic expression?
An algebraic expression is a mathematical phrase that can contain numbers, variables, and operations such as addition, subtraction, multiplication, and division.
In this case, the algebraic expression that represents the length of the soccer game would be:
m = 90 + x
where m represents the total length of the game in minutes, 90 represents the fixed length of the game, and x represents the variable length of time-outs in minutes.
To find the length of the game with 8 minutes of time-outs, we substitute x = 8 into the expression:
m = 90 + 8 = 98
Therefore, the game with 8 minutes of time-outs is 98 minutes long.
To learn more about the algebraic expression, visit:
https://brainly.com/question/4344214
#SPJ1
A right cone has a height of 12 inches and a volume of 64π in³. What is the radius of the cone?
Answers
The radius of the cone is given by the equation r = 4 inches
What is a Cone?A cone is a three-dimensional shape in geometry that narrows smoothly from a flat base (usually circular base) to a point(which forms an axis to the center of base) called the apex or vertex.
The volume of a cone is given by the equation
Volume of Cone = ( 1/3 ) πr²h
where r is the radius of the cone
h is the height of the cone
Surface area of the cone = πrl
where l = √ ( b² + r² )
Given data ,
Let the radius of the cone be represented as r
Now , the equation will be
The volume of the cone = 64π inches³
The height of the cone h = 12 inches
So , Volume of Cone = ( 1/3 ) πr²h
Substituting the values in the equation , we get
64π = ( 1/3 )π r² ( 12 )
Divide by π on both sides of the equation , we get
64 = 4r²
Divide by 4 on both sides of the equation , we get
r² = 16
Taking square roots on both sides of the equation , we get
r = 4 inches
Therefore , the value of r is 4 inches
Hence , the radius of cone is 4 inches
To learn more about cone click :
https://brainly.com/question/1984638
#SPJ1
Find the slope of the line that passes through points (4,5) and (3,-4)?
Answers
Answer:
slope=9
Step-by-step explanation:
whole equation=y = 9x – 31
hope that helps
please mark as brainliest if correct
thank you
have a great day/night
converting 1,000 mg to 1 gram would require moving the decimal place ________ places to the left.
Answers
Converting 1,000 mg to 1 gram would require moving the decimal place zero places to the left.
Unit conversion is a process with multiple steps that involves multiplication or division by a numerical factor or, particularly a conversion factor. The process may also require selection of the correct number of significant digits, and rounding. Different units of conversion are used to measure different parameters. By definition conversion of units means the conversion between different units and measurements of the same quantity done by the process of multiplication or division. In maths, conversion is the process of changing the value of one form to another for example inches to millimeters, or liters to gallons. Units are used for measuring length, measuring weight, measuring capacity, measuring temperature, and measuring speed.
If we want to calculate how many Grams are 1000 Milligrams we have to multiply 1000 by 1 and divide the product by 1000. So for 1000, we have (1000 × 1) ÷ 1000 = 1000 ÷ 1000 = 1 Gram.
So finally 1000 mg = 1 g
Thus, converting 1,000 mg to 1 gram would require moving the decimal place zero places to the left.
To learn more about unit conversion, visit brainly.com/question/19420601
#SPJ4
For a one-tailed test with a 0.05 level of significance, the critical z statistic is 1.645, but the critical t statistic is 1.96. True or False
Answers
For a one-tailed test with a 0.05 level of significance, the critical z statistic is 1.645, but the critical t statistic is 1.96. The statement is false.
The statement is incorrect. For a one-tailed test with a 0.05 level of significance, the critical z statistic is indeed 1.645. However, the critical t statistic value depends on the degrees of freedom (df), which is not provided in the statement. The 1.96 value mentioned is actually the critical z statistic for a two-tailed test with a 0.05 level of significance.
To learn more about the one-tailed test, refer:-
https://brainly.com/question/31270353
#SPJ11
Lindsey Corp. uses the percentage-of-credit-sales method and estimates that 8% of the credit sales are uncollectible. After the year-end adjustment, what amount of bad debt expense would Lindsey report for the year
Answers
Using the percentage-of-credit-sales method, Lindsey Corp. would report a bad debt expense of $40,000 for the year, assuming their total credit sales were $500,000 and they estimated 8% of those sales to be uncollectible.
Lindsey Corp. uses the percentage-of-credit-sales method to estimate their bad debt expense. According to their estimation, 8% of their credit sales are anticipated to be uncollectible. To calculate the bad debt expense for the year, Lindsey Corp. would follow these steps:
Multiply the total credit sales by the estimated percentage of uncollectible sales,
Next, Lindsey Corp. would multiply the total credit sales by the estimated percentage of uncollectible sales (8% in this case). This calculation gives us the anticipated amount of credit sales that are expected to become bad debts.
Mathematically, the formula would be:
Bad Debt Expense = Total Credit Sales * Percentage of Uncollectible Sales
If Lindsey Corp. had $500,000 in total credit sales for the year, the calculation would be:
Bad Debt Expense = $500,000 * 0.08 = $40,000
Finally, Lindsey Corp. would report the calculated amount as their bad debt expense for the year. This expense is recorded on the income statement to reflect the potential loss from uncollectible credit sales.
To know more about debt expense here
https://brainly.com/question/30943691
#SPJ4
If m || k and m || , then
k
m
3
2
Please help

Answers
Answer: \(k \parallel l\)
Step-by-step explanation:
Lines that are parallel to the same line are parallel.
