Answers
Answer:
Step-by-step explanation:
It would be c
Related Questions
f(x)=3^x+1 and g(x) = 2x-4, find f(2) - g(-1)
Answers
Answer:
16
Step-by-step explanation:
3^x +1 = f(X)
2x-4 = g(x)
find f(2)-g(-1)
we substitute in function f(X) by value (2), and in function g(X) by value (-1)
1. 3^x +1 becomes 3^2+1 =9+1=10
2. 2(-1)-4= -2-4=-6
then f(2)-g(-1)
= 10-(-6) =10+6=16
Graph the solution to the equations below. y = 1 4 x + 2 and y = −2x −7
Answers
PLEASE HELP................

Answers
1. The scale factor here in the dilation is 4/3.
2. Yes, dilation occurred on the coordinate plane below. The scale factor for the dilation is -4/3.
What is dilation?During the process of dilatation, an object must be reduced in size or changed. It is a transformation that uses the given scale factor to shrink or expand the objects. The image is the new figure that forms as a result of dilatation, whereas the pre-image is the original figure. There are two kinds of dilation:
A rise in an object's size is referred to as expansion.
Contraction is the term used for a reduction in size.
Here in the question,
The coordinates of the point B change from (-3,6) to (-4,8).
The scale factor here is -4/-3=4 or 8/6=4/3.
Now, when the dilation happens below the plane, the coordinates will be (x,-y)
So, the dilation factor will be -4/3.
To know more about dilation, visit:
https://brainly.com/question/13176891
#SPJ1
A teaching hospital in South-West Part of Nigeria receives on the average 5 pregnant women with high blood pressure per week. What is the probability that on a particular week, the teaching hospital will receive:
1.) No high BP pregnant woman
Answers
Answer:
The probability that on a particular week, the hospital will receive on high BP pregnant woman is 0.0068
Step-by-step explanation:
We use the Exponential distribution,
Since we are given that on average, 5 pregnant women with high blood pressure come per week,
So, average = m = 5
Now, on average, 5 people come every week, so,
5 women per week,
so, we get 1 woman per (1/5)th week,
Hence, the mean is m = 1/5 for a woman arriving
and λ = 1/m = 5 = λ
we have to find the probability that it takes higher than a week for a high BP pregnant woman to arrive, i.e,
P(X>1) i.e. the probability that it takes more than a week for a high BP pregnant woman to show up,
Now,
P(X>1) = 1 - P(X<1),
Now, the probability density function is,
\(f(x) = \lambda e^{-\lambda x}\)
And the cumulative distribution function (CDF) is,
\(CDF = 1 - e^{-\lambda x}\)
Now, CDF gives the probability of an event occuring within a given time,
so, for 1 week, we have x = 1, and λ = 5, which gives,
P(X<1) = CDF,
so,
\(P(X < 1)=CDF = 1 - e^{-\lambda x}\\P(X < 1)=1-e^{-5(1)}\\P(X < 1)=1-e^{-5}\\P(X < 1) = 1 - 6.738*10^{-3}\\P(X < 1) = 0.9932\\And,\\P(X > 1) = 1 - 0.9932\\P(X > 1) = 6.8*10^{-3}\\P(X > 1) = 0.0068\)
So, the probability that on a particular week, the hospital will receive on high BP pregnant woman is 0.0068
What is the domain restriction that will allow you to find an inverse of the function f(x) = 3(x − 9)2 + 4?
Answers
Answer:
f(x) = 3(x − 9)^2 + 4
To find the inverse of f(x), first we denote: y = 3(x - 9)^2 + 4, we then find a way to express x in term of y.
y = 3(x - 9)^2 + 4
<=> y - 4 = 3(x - 9)^2
<=> (y - 4)/3 = (x - 9)^2
<=> sqrt[(y - 4)/3] = x - 9
<=> x = sqrt[(y - 4)/3] + 9
Denote left side is g(x), and variable y on the right side is x, we have:
g(x) = sqrt[(x - 4)/3] + 9
g(x) is inverse of f(x)
Here, (x - 4)/3 must be not a negative number (because of the definition of square root (sqrt) of a real number)
=> x - 4 >= 0 or x >= 4
=> The restriction domain of g(x), which is the inverse of f(x) is x >= 4
What is the value of h in the diagram below? If necessary, round your answer
to the nearest tenth of a unit.
N
M
P 2 O
12
u
A. 12
0
B. 2.2
C. 7
a
D. 4.5

Answers
Answer: 4.5
Step-by-step explanation: 7 is incorrect
20 workers can produce 1000 products in 10 hours.
Assuming the efficiency per worker remains the same, how many products can 15 workers produce in 5 hours?
Answers
Using proportions, it is found that 375 products are produced with 15 workers in 5 hours.
What is a proportion?A proportion is a fraction of a total amount, and the measures are related using a rule of three.
In this problem, we have that the rule of three are given as follows:
1000 products - 20 workers - 10 hours.
x products - 15 workers - 5 hours.
The measures are direct proportional, hence:
\(\frac{1000}{x} = \frac{20}{15} \times \frac{10}{5}\)
\(\frac{1000}{x} = \frac{40}{15}\)
Applying cross multiplication:
40x = 15(1000)
x = 15(1000)/40
x = 375.
375 products are produced with 15 workers in 5 hours.
More can be learned about proportions at https://brainly.com/question/24372153
5h-6-8+7h what’s the answer ?
Answers
me prions for apples per pound are listed
in the table.
$2.99
$1.29
$1.89
$1.59
$0.99
What is the mean price of apples
per pound?
F $1.75
G $1.59
H $1.14
$2.00

Answers
Answer:
Its F $1.75
Step-by-step explanation:
Because you add all the numbers up then once you get your answer you divided it by how many numbers there are like you'll get 8.75 divide it by 5 and you have your answer
Answer:
The Answer is H $1.14
Step-by-step explanation:
First You have to add both mean in the second column:
$1.29+0.99=$2.28
Then you have to divide the price that u given in the second column that u get after u add both the price :
$2.29/2=1.14
∴The mean price of apples per pound is $1.14
Christopher wants to estimate the mean amount of carbon dioxide that is emitted by burning 1\text{ L}1 L1, start text, space, L, end text of a new type of gasoline. He plans on burning 1\text{ L}1 L1, start text, space, L, end text at a time and measuring the resulting emissions. He'll repeat this process for a sample of nnn attempts and construct a confidence interval for the mean. He wants the margin of error to be no more than 202020 grams at a 90\%90%90, percent level of confidence. Preliminary data suggests that \sigma=50σ=50sigma, equals, 50 grams is a reasonable estimate for the standard deviation of the emissions from burning 1\text{ L}1 L1, start text, space, L, end text of this type of gasoline. Which of these is the smallest approximate sample size required to obtain the desired margin of error?
Answers
Answer:
The smallest sample size required to obtain the desired margin of error is of 17.
Step-by-step explanation:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1-0.9}{2} = 0.05\)
Now, we have to find z in the Ztable as such z has a pvalue of \(1-\alpha\).
So it is z with a pvalue of \(1-0.05 = 0.95\), so \(z = 1.645\)
Now, find the margin of error M as such
\(M = z*\frac{\sigma}{\sqrt{n}}\)
In which \(\sigma\) is the standard deviation of the population and n is the size of the sample.
Which of these is the smallest approximate sample size required to obtain the desired margin of error?
The desired margin of error is 20, so \(M = 20\)
We have that \(\sigma = 50\).
The smallest sample size is n. So
\(M = z*\frac{\sigma}{\sqrt{n}}\)
\(20 = 1.645*\frac{50}{\sqrt{n}}\)
\(20\sqrt{n} = 50*1.645\)
\(\sqrt{n} = \frac{50*1.645}{20}\)
\((\sqrt{n})^2 = (\frac{50*1.645}{20})^2\)
\(n = 16.9\)
Rounding up
The smallest sample size required to obtain the desired margin of error is of 17.
2-11 Unit Rates
Part 1 of 3
Due 11/1
Challenge An arts academy repares there to be 4 teachers for every 60 students and 6 tutors for every 48 students. How many students does the academy heve per teacher? Por tudor? How many
tutors does the academy need if it has 00 students?
Answers
There are total 15 students per teacher and 8 students per tutor. For 100 students, total 13 tutors are required.
What is an arithmetic operation?The four fundamental operations of arithmetic are addition, subtract, multiply, and division of two or more numbers. Included in them is the study of integers, especially the order of operations, which is important for all other aspects of mathematics, notably algebra, information management, and geometry.
As per the given data provided in the question,
4 teachers = 60 students
For 1 teacher = 60/4 = 15 students
Similarly,
6 tutors = 48 students
For 1 tutor = 48/6 = 8 students.
For total 100 students, total number of tutors = 100/8
= 12.5 or 13 tutors are required.
To know more about arithmetic operation:
https://brainly.com/question/13585407
#SPJ1
Kevin plants a total 72 flowers in a equal row. He plants 6 rows of yellow flowers and 2 rows of red flowers. How many flowers are in each row?
Answers
Answer:
9
Step-by-step explanation:
9 is the answer bc
6+2=8
72/8=9
(lol I hope I helped)
number 4 pls help plssssssssssssss I will pay u plssssssssssss help me out. its number 4

Answers
Answer:
40%
Step-by-step explanation:
i used a calculator
. Solve: - 5x² + 5 = - 2x The solution contains a reduced fraction another reduced
fraction with a radical numerator. What is this fraction with a radical numerator?
a
Answers
Consider the given quadratic equation that we have :
\({:\implies \quad \sf -5x^{2}+5=-2x}\)
Multiplying both sides by -1 will yield ;
\({:\implies \quad \sf 5x^{2}-5=2x}\)
Write the above quadratic equation in the form of standard quadratic equation ax² + bx + c = 0 ,
\({:\implies \quad \sf 5x^{2}-2x-5=0}\)
Now , comparing this with the standard form of quadratic equation we will get a = 5 , b = -2 , c = -5 . So now , Discriminant (D) = (-2)² - 4 × 5 × -5 = 4 + 100 = 104
Now , by the quadratic formula ;
\({:\implies \quad \sf x=\dfrac{-(-2)\pm \sqrt{104}}{2\times 5}}\)
\({:\implies \quad \sf x=\dfrac{2\pm 2\sqrt{26}}{2\times 5}}\)
\({:\implies \quad \sf x=\dfrac{\cancel{2}(1\pm \sqrt{26})}{\cancel{2}\times 5}}\)
\({:\implies \quad \bf \therefore \quad \underline{\underline{x=\dfrac{1\pm \sqrt{26}}{5}}}}\)
Used Concepts :-For any quadratic equation of the form ax² + bx + c , the Discriminant (D) is given by D = b² - 4ac , and the root \(\bf x\) of the quadratic equation is given by the quadratic formula as
\({\boxed{\bf{x=\dfrac{-b\pm \sqrt{D}}{2a}}}}\)A rectangular city is 2 miles long and 7 miles wide. What is the distance between opposite corners of the city? The exact distance is ______________ miles How far is it to the closest tenth of a mile? Answer: The distance is approximately ___________ miles.
Answers
Answer:
The distance is approximately 10.4 miles.
Answer:
exact distance is = 7.28010988928
rounded to the tenth of a mile is
distance is approximately 7.3 miles
Step-by-step explanation:
hypotenuse of a triangle that's 2 by 7
Pythagorean theorem
a^2 + b^2 = c^2
2^2 + 7^2 = c^2
4 + 49 = c^2
c^2 = 53
c = √53
c = 7.28010988928
tenth of a mile is
c = 7.3
-3, 9, -27, 81 find the next term
Answers
Answer: The next term is -243.
Answer:
-243
Step-by-step explanation:
The common ratio in this geometric sequence is -3. Therefore, the next term will be 81(-3) = -243.
6x²-7x=20 solve the following quadratic equation
Answers
Answer:
x = -4/3 and x = 5/2.
Step-by-step explanation:
6x² - 7x = 20
6x² - 7x - 20 = 0
To solve this, we can use the quadratic formula to solve this.
[please ignore the A-hat; that is a bug]
\(\frac{-b±\sqrt{b^2 - 4ac} }{2a}\)
In this case, a = 6, b = -7, and c = -20.
\(\frac{-(-7)±\sqrt{(-7)^2 - 4 * 6 * (-20)} }{2(6)}\)
= \(\frac{7±\sqrt{49 + 80 * 6} }{12}\)
= \(\frac{7±\sqrt{49 + 480} }{12}\)
= \(\frac{7±\sqrt{529} }{12}\)
= \(\frac{7±23 }{12}\)
\(\frac{7 - 23 }{12}\) = \(\frac{-16 }{12}\) = -8 / 6 = -4 / 3
\(\frac{7 + 23 }{12}\) = \(\frac{30}{12}\) = 15 / 6 = 5 / 2
So, x = -4/3 and x = 5/2.
Hope this helps!
Answer:
\(x1 = - \frac{4}{3} \)\(x2 = \frac{5}{2} \)Step-by-step explanation:
\(6 {x}^{2} - 7x = 20\)
Move constant to the left and change its sign
\( {6x}^{2} - 7x - 20 = 0\)
Write -7x as a difference
\(6 {x}^{2} + 8x - 15x - 20 = 0\)
Factor out 2x from the expression
\(2x(3x + 4) - 15x - 20 = 0\)
Factor out -5 from the expression
\(2x(3x + 4) - 5(3x + 4) = 0\)
Factor out 3x + 4 from the expression
\((3x + 4)(2x - 5) = 0\)
When the product of factors equals 0 , at least one factor is 0
\(3x + 4 = 0\)
\(2x - 5 = 0\)
Solve the equation for X1
\(3x + 4 = 0\)
Move constant to right side and change its sign
\( 3x = 0 - 4\)
Calculate the difference
\(3x = - 4\)
Divide both sides of the equation by 3
\( \frac{3x}{3} = \frac{ - 4}{3} \)
Calculate
\(x = - \frac{4}{3} \)
Again,
Solve for x2
\(2x - 5 = 0\)
Move constant to right side and change its sign
\(2x = 0 + 5\)
Calculate the sum
\(2x = 5\)
Divide both sides of the equation by 2
\( \frac{2x}{2} = \frac{5}{2} \)
Calculate
\(x = \frac{5}{2} \)
\(x1 = - \frac{4}{3} \)
\(x2 = \frac{5}{2} \)
Hope this helps...
Best regards!!
This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part. Tutorial Exercise Find the exact value of the trigonometric function given that sin u 5/13 and cos v -3/5. (Both u and v are in Quadrant II.) cos(u - v)
Answers
The exact value of the trigonometric function cos ( u - v) in the second quadrant is equal to cos ( u - v ) = 56 / 65.
In the second quadrant,
Trigonometric function sine is always positive.
And trigonometric function cosine is always negative.
Here value of trigonometric function
sin u = 5 / 13
cos v = -3 /5
cos u = √ 1 - sin² u
⇒ cos u = √ 1 - ( 5 / 13 )²
⇒ cos u = √ 144/169
⇒ cos u = -12 / 13
And
sin v = √ 1 - cos² v
⇒ sin v = √ 1 - ( -3/5 )²
⇒ sin v = √ 16/25
⇒ sin v = 4 / 5
Now exact value of trigonometric function
cos ( u - v ) = cos u cos v + sin u sin v
Substitute the value we get,
⇒ cos ( u - v ) = (-12/13)(-3/5) + ( 5/13)(4/5)
⇒ cos ( u - v ) = 36 / 65 + 20 / 65
⇒ cos ( u - v ) = 56 / 65
Therefore , the value of the trigonometric function cos ( u - v ) = 56 / 65.
Learn more about trigonometric function here
brainly.com/question/20593351
#SPJ4
The above question is incomplete, the complete question is:
Find the exact value of the trigonometric function cos(u - v) .
Given that sin u 5/13 and cos v -3/5. (Both u and v are in Quadrant II.)
What is -9 as a fraction?
Answers
Answer:
\(-\frac{9}{1}\)
Step-by-step explanation:
Its just the same way as making positive 9
a fraction, but just add the negative sign.
Hope this helps :))
If the set W is a vector space, find a set S of vectors that spans it. Otherwise_ state that W is not a vector space_ 2b 3b W is the set of all vectors of the form 4a- b where a and b are arbitrary rea numbers OA S = B. S = W is not a vector space S = Find all values of h such that will be in the subspace of R spanned by V1 ' Vz' V3 ifv " V3 and y = h = - 12 or 0 h= -16 h= -12 all h # 12 V2 =
Answers
One possible set is {[1 -4 5 4], [0 1 0 1], [1 0 -1 -1], [1 1 0 -1]}. These vectors can be combined in various linear combinations to form any vector in W.
First, let's define what a vector space is. A vector space is a collection of vectors that satisfies certain axioms or rules. These axioms include closure under addition and scalar multiplication, associativity, commutativity, distributivity, and the existence of an additive identity and inverse. In simpler terms, a vector space is a set of vectors that can be added together and scaled by constants, and the resulting vectors still belong to the set.
Now let's take a look at the set W given in the problem. Each vector in W is represented by four real numbers, denoted by
=> [a - 4b 5 4a + b -a - b].
To determine if W is a vector space, we need to check if it satisfies the aforementioned axioms.
We can start by checking closure under addition. That is, if we add two vectors from W, do we get another vector in W? Let's take two arbitrary vectors,
=> [a₁ - 4b₁ 5 4a₁ + b₁ -a₁ - b₁] and
=> [a₂ - 4b₂ 5 4a₂ + b₂ -a₂ - b₂].
If we add them together component-wise, we get
=> [a₁ + a₂ - 4(b₁ + b₂) 10 4(a₁ + a₂) + (b₁ + b₂) -(a₁ + a₂) - (b₁ + b₂)].
This is also a vector in W, since it has the same form as the vectors in W. Therefore, W is closed under addition.
Next, we need to check closure under scalar multiplication. That is, if we multiply a vector from W by a scalar, do we get another vector in W? Let's take an arbitrary vector
=> [a - 4b 5 4a + b -a - b] and multiply it by a scalar k.
We get
=> [ka - 4kb 5 4ka + kb -ka - kb].
This is also a vector in W, since it has the same form as the vectors in W. Therefore, W is closed under scalar multiplication.
We can also check the other axioms and see that W satisfies all of them. Therefore, W is indeed a vector space.
Now, to find a set of vectors that spans W, we need to find a set of vectors that can be combined in linear combinations to form any vector in W. One way to do this is to find a basis for W, which is a set of linearly independent vectors that spans W. However, it can be shown that any set of four non-coplanar vectors in R⁴ (four-dimensional Euclidean space) forms a basis for R⁴, and thus spans any subspace of R⁴, including W.
Therefore, we can choose any four non-coplanar vectors in W as a set that spans W.
To know more about vector here.
https://brainly.com/question/29740341
#SPJ4
need help quick, ez question
will give brainliest

Answers
The volume of the given triangular prism is 384 cm³.
What is the volume?Volume is the measure of the capacity that an object holds.
Formula to find the volume of the object is Volume = Area of a base × Height.
Here, the area of the base is
Area of a rectangle = 1/2 ×Base×Height
= 1/2 ×12×4
= 24 cm²
Now the volume is 24×16
= 384 cm³
Therefore, the volume of the given triangular prism is 384 cm³.
To learn more about the volume visit:
https://brainly.com/question/13338592.
#SPJ1
use the shell method to find the volume generated by revolving the shaded regions bounded by the curves and lines in exerciss 7-12about the y-axis
Answers
The answer is 1) V = \(2\pi\int\limits(2)+ {x} \, dx\); 2) V = \(2\pi \int\limits(1 - 2x) - 2x dx\); 3) V =\(2\pi \int\limits {\sqrt{2} } \, dx\) ; 4) V = \(2\pi\int\limits {\sqrt{(-2/2)(2-2)} \ dx\) .
1) The volume of the shell is then given by the product of the area of its curved surface and its height. The height is equal to 2 - (-2) = 4, and the radius is equal to the minimum of the distances from x = 2 to the two curves, which is x = 2 - () = 2 + . The volume of the solid is then given by the definite integral:
V = \(2\pi\int\limits(2)+ {x} \, dx\) = \(2\pi [(/3) + 2x]\) evaluated from 0 to 1 = (4/3)π.
2) The height of the region is equal to - (2x) = -2x, and the radius is equal to the minimum of the distances from x = 1 to the two curves, which is x = 1 - (2x) = 1 - 2x. The volume of the solid is then given by:
V = \(2\pi \int\limits(1 - 2x) - 2x dx\)=\(2\pi [/5 - 2/3 + /2]\) evaluated from 0 to 1 = (8π/15).
3) The height of the region is equal to (2-x) - = 2-x. The radius is equal to the minimum of the distances from x = 0 to the two curves, which is x = The volume of the solid is then given by:
V =\(2\pi \int\limits {\sqrt{2} } \, dx\) = \(2\pi [(x^4/4)]\) evaluated from 0 to √2 = (π/2).
4) The height of the region is equal to () - (2-) = 2 - 2. The radius is equal to the minimum of the distances from x = 0 to the two curves, which is x = √((2-)/2). The volume of the solid is then given by:
V = \(2\pi\int\limits {\sqrt{(-2/2)(2-2)} \ dx\) = \(4\pi [(2/3)\± (2\sqrt{2} /3)]\)
The complete Question is:
Use the shell method to find the volumes of the solids generated by revolving the regions bounded by the curves and lines in about the
1. y = x, y = -x/2, and x = 2
2. y = 2x, y = x/2, and x = 1
3. y = x/2, y = 2-x, and x = 0
4. y = 2-x/2, y = x/2, and x = 0
To know more about Shell Methods:
brainly.com/question/17074517
#SPJ4
Find the standard deviation of the sampling distribution of sample means using the given information. Round to one decimal place, if necessary. μ = 64 and o = 12; n = 9
Answers
The standard deviation of the data sample is 2.55.
What is the standard deviation of the data sample?The standard deviation of the data sample is calculated by applying the following formula;
S.D = √ (x - μ)²/(n - 1)
where;
μ is the mean of the distributionx is the sample datan is the number of sample dataThe given parameters;
mean, μ = 64
x, = 12
number of samples = 9
The standard deviation of the data sample is calculated as;
S.D = √ (12 - 64)²/(9 - 1)
S.D = 2.55
Thus, the standard deviation of the data sample is calculated by applying the formula for standard deviation.
Learn more about standard deviation here: https://brainly.com/question/24298037
#SPJ1
If 3p - 2q = 4 and 7p - 39 = 1.then what is 4p - 59 equal to?
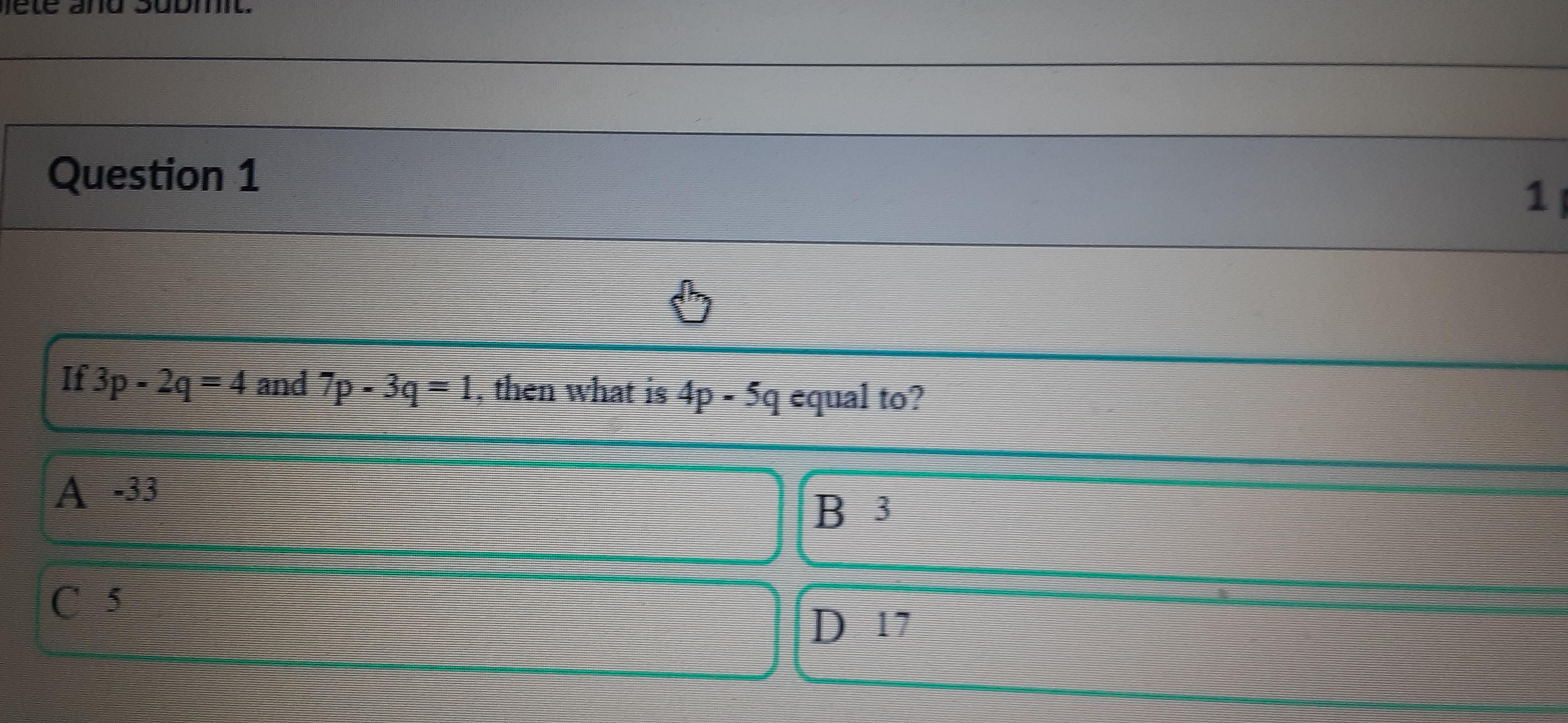
Answers
Based on the information given in the exercise, you can set up the following System of equations:
\(\begin{cases}3p-2q=4 \\ 7p-3q=1\end{cases}\)You can use the Substitution method to find the value of the variable "p" and the variable "q":
- Solve for "q" from the first equation:
\(\begin{gathered} 3p-2q=4 \\ -2q=4-3p \\ q=\frac{4}{-2}-(\frac{3p}{-2}) \\ \\ q=-2+\frac{3}{2}p \end{gathered}\)- Substitute the new equation into the second equation:
\(\begin{gathered} 7p-3q=1 \\ 7p-3(-2+\frac{3}{2}p)=1 \end{gathered}\)- Solve for "p":
\(\begin{gathered} 7p+6-\frac{9}{2}p=1 \\ \\ \frac{5}{2}p=1-6 \\ \\ 5p=(2)(-5) \\ \\ p=\frac{-10}{5} \\ \\ p=-2 \end{gathered}\)- Substitute the value of "p" into the equation
\(q=-2+\frac{3}{2}p\)And evaluate. Then:
\(\begin{gathered} q=-2+\frac{3}{2}(-2) \\ q=-2-3 \\ q=-5 \end{gathered}\)Now knowing the values of "p" and "q", you can substitute them into this expression:
\(4p-5q\)And then evaluate. So, you get:
\(4(-2)-5(-5)=-8+25=17\)Therefore:
\(4p-5q=17\)The answer is: Option D.
Ten canoeing teams are racing downriver. Five teams have silver canoes and 2 teams have brown canoes.what Fraction of the canoes are either silver or/ and brown?
Answers
The fraction of silver or brown canoes is 7/10.
What is a fraction?A fraction is written in the form of a numerator and a denominator where the denominator is greater that the numerator.
Example: 1/2, 1/3 is a fraction.
We have,
Total canoes team = 10
5 teams have silver canoes team.
2 teams have brown canoes team.
Now,
The fraction of silver and brown canoes.
= (5 + 2) / 10
= 7/10
Thus,
7/10
Learn more about fractions here:
https://brainly.com/question/24370499
#SPJ9
Please answer immediately I beg.
A pyramid and a cone have the same base area and height. The volume
of the pyramid is 175m³. What is the volume of the one? Explain your answer.
Answers
The volume of cone is 175 m³
Firstly,
Volume of Pyramid.
The volume (V) of a pyramid is
V = ⅓Ah
Data:
V = 175m³
Calculation:
175 = ⅓× A× h
Ah = 175*3
Ah = 525m³
Secondly,
The volume (V) of a cone is
V = ⅓Ah
Data:
Ah = 525 m³
Calculation:
V = ⅓ A× h
V = 175 m³
Know more about volumes,
https://brainly.com/question/17101095
#SPJ1
Select the correct answer.
Which sentence correctly describes a data set that follows a normal distribution with a standard deviation of 4 and a mean of 14?
68% of the data points lie between 10 and 14.
68% of the data points lie between 8 and 12.
68% of the data points lie between 10 and 18.
68% of the data points lie between 10 and 16.
Answers
Answer:
68% of the data points lie between 10 and 18.
Step-by-step explanation:
one standard deviation to left of mean = 14 - 4 =10
one standard deviation to right of mean = 14 + 4 = 18
68% of data is in this region.
so the answer is 68% of the data points lie between 10 and 18.
solve for z? 2x-4y+4z-6w=4 6w-4x+4y-4z=-12 6w+4x-2y+6z=64 4z+2w+6y-4x=56
Answers
Answer:
z ≈ 9.22
Step-by-step explanation:
Given the equations
2x-4y+4z-6w=4 ................ 1
6w-4x+4y-4z=-12 ...............2
6w+4x-2y+6z=64 ............... 3
4z+2w+6y-4x=56 ................ 4
We will first need to reduce the equation by cancelling out some variables.
Add equations 1 and 2 will give;
(2x-4x)+(-4y+4y)+(4z-4z)+ (-6w+6w) = 4+12
-2x +0 = 16
-2x = 16
x = -8
Also, equation 2 minus 3
6w-6w+(-4x-4x)+4y+2y+(-4z-6z) = 12-64
-8x+6y-10z = -52
-8(-8)+6y-10z = -52
64+6y-10z = -52
6y-10z = -52-64
6y-10z = -116
3y-5z = -58 ... 5
Equation 3 * 1 and eqn 4 * 3
6w+4x-2y+6z=64 ............... 3
4z+2w+6y-4x=56 ................ 4
6w+4x-2y+6z=64
12z+6w+18y-12x= 168
Subtracting both equations;
16x-20y-6z = -104
8x-10y-3z = -52
8(-8)-10y-3z = -52
-64-10y-3z = -52
-10y-3z = -52+64
-10y-3z = 12 ....... 6
equating 5 and 6 and solving simultaneously;
3y-5z = -58 ... 5 * 10
-10y-3z = 12 ....... 6 * 3
30y-50z = -580
-30y-9z = 36
Add both equations
-50z-9z = -580+36
-59z = -544
z = -544/-59
z = 9.22
Hence z ≈ 9.22
connie can type 675 words in 15 mins please help!!
Answers
Answer: 45 words per minute.
Step-by-step explanation: I'm not exactly sure what you're asking, but Connie types 45 words per minute (675/15 = 45).
If the hypotenuse of a right triangle is equal to the hypotenuse of another right triangle, then are the triangles congruent?
Answers
The triangles are considered to be congruent if one right triangle's hypotenuse and another right triangle's hypotenuse are equal.
Given, assuming that the hypotenuse of one right triangle is equivalent to the hypotenuse of another right triangle, then the triangles are harmonious.
The given statement must be verified as true or false by us.
According to the RHS congruence theorem, two right-angled triangles are congruent if the hypotenuse and side of one triangle are equal to the hypotenuse and side of another.
The hypotenuse and the side of the triangle that corresponds to it must be equal according to the RHS rule.
The hypotenuses of the two triangles are equal, per the question.
To learn more about right triangle's hypotenuse here
https://brainly.com/question/2869318
#SPJ4
