Answers
Related Questions
help meeeeeeeeeeeeeeeeeee pleaseeeeeeeeeeeeeee!!!!!!!!!!!!!!

Answers
Time intervals = 14/7 = 2
Final Amount = 40(1/2)² = 10
what is 3.1 × 10 1 in standard form
Answers
Answer:
Step-by-step explanation:
1.3×100=1.3
in standard form.
Explanation:
In scientific notation, we write a number so that it has single digit to the left of decimal sign and is multiplied by an integer power of
10.
In other words, in scientific notation, a number is written as
a ×10n, where 1≤a<10 and n is an integer and 1≤a< 10.To write the number in normal or standard notation one just needs to multiply by the power
10n(or divide if n is negative). This means moving decimal
n digits to right if multiplying by
10n and moving decimal n digits to left if dividing by 10n
(i.e. multiplying by 10−n).
In the given case, as we have the number as
1.3×100, we need not move decimal digit to either side and hence in standard notation 1.3×100=1.3 itself.
Select the correct answer

Answers
Answer:
B. iStep-by-step explanation:
n/4 has a remainder of 3, then it has a format of:
n = 4k + 3Substitute n:
i^n = i^(4k)*i^3 = i^(4k)*i^2*i = (-1)(-1)*i = iCorrect option is B. i
chicken wing chicken wing chicken wing
Answers
Answer:
Hot Dog and Bologna
Step-by-step explanation:
Chicken and macaroni, chillin with my...
What is the value of y ?

Answers
Answer:
y = 80
The opposite angle of y is 80.
how many ways are there to arrange 4 americans, 3 russians, and 5 chinese into a queue, using inclusion-exclusion principle?
Answers
Using the inclusion-exclusion principle the number of arrangements can be 1080069120.
What is The principle of inclusion and exclusion?(PIE) is a counting method that determines how many elements fulfill at least one of numerous properties while making sure that components that satisfy several properties are not tallied more than once.Let us denote by R, the set of arrangements where the Russians are together, by A, the set of arrangements where the Americans are together, and by C for the Chinese.I denote the complement of a set X by X' its cardinality by ∣X∣ and the universal set by S
The number of unrestricted arrangements of these 11 people.
=11!=SAmericans can seat in:
A = 9! * 4!
Russians can seat in:
R = 10!*3!And Chinese can seat is:
C = 8! *5!Now, we calculate ∣A∩R∣. In this case,
∴∣A∩R∣=7!*4!*3! and for |R∩C|=3!*5!*8! and |A∩C|=4!*5!*9!∴∣C∩R∩A∣=3!×4!*5!*3!By the principle of inclusion and exclusion, we have:
∣C∪R∪A∣=∣C∣+∣R∣+∣A∣−∣C∩R∣−∣C∩A∣−∣R∩A∣+∣C∩R∩A∣or,∣C'∩R'∩A'∣= S-∣C∪R∪A∣ = 1080069120Therefore, using the inclusion-exclusion principle the number of arrangements can be 1080069120.
Learn more about the inclusion-exclusion principle, here:
https://brainly.com/question/13097369
#SPJ4
writing equations of lines parallel and perpendicular to a given line through a point
Answers
To find the equation of a line parallel or perpendicular to a given line through a point, determine the slope and substitute the point's coordinates into the slope-intercept form.
To find the equation of a line parallel or perpendicular to a given line through a specific point, follow these steps:
1. Determine the slope of the given line. If the given line is in the form y = mx + b, the slope (m) will be the coefficient of x.
2. Parallel Line: A parallel line will have the same slope as the given line. Using the slope-intercept form (y = mx + b), substitute the slope and the coordinates of the given point into the equation to find the new y-intercept (b). This will give you the equation of the parallel line.
3. Perpendicular Line: A perpendicular line will have a slope that is the negative reciprocal of the given line's slope. Calculate the negative reciprocal of the given slope, and again use the slope-intercept form to substitute the new slope and the coordinates of the given point. Solve for the new y-intercept (b) to obtain the equation of the perpendicular line.
Remember that the final equations will be in the form y = mx + b, where m is the slope and b is the y-intercept.Therefore, To find the equation of a line parallel or perpendicular to a given line through a point, determine the slope and substitute the point's coordinates into the slope-intercept form.
To learn more about intercept click here
brainly.com/question/29142047
#SPJ11
6.1.11 suppose we have a statistical model {fθ : θ ∈ [0, 1]} and we observe x0. is it true that 8 1 0 l(θ | x0) dθ = 1? explain why or why not.
Answers
No, it is not true that ∫_0^1 l(θ | x0) dθ = 1. The integral of the likelihood function l(θ | x0) over the parameter space [0, 1] does not necessarily equal 1.
The likelihood function l(θ | x0) measures the probability of observing the data x0 given the parameter value θ. It is a function of the parameter θ, and not a probability distribution over θ.
Therefore, the integral of the likelihood function over the parameter space does not have to equal 1, unlike the integral of a probability density function over its support.
In fact, the integral of the likelihood function over the parameter space is often referred to as the marginal likelihood or the evidence, and is used in Bayesian inference to compute the posterior distribution of the parameter θ given the data x0. The marginal likelihood is given by: ∫_0^1 l(θ | x0) p(θ) dθ
where p(θ) is the prior distribution of the parameter θ. The marginal likelihood is used to normalize the posterior distribution so that it integrates to 1:
p(θ | x0) = l(θ | x0) p(θ) / ∫_0^1 l(θ | x0) p(θ) dθ
In conclusion, the integral of the likelihood function over the parameter space does not necessarily equal 1, and is used in Bayesian inference to compute the posterior distribution of the parameter θ given the data x0.
You can read more about probability at https://brainly.com/question/24756209
#SPJ11
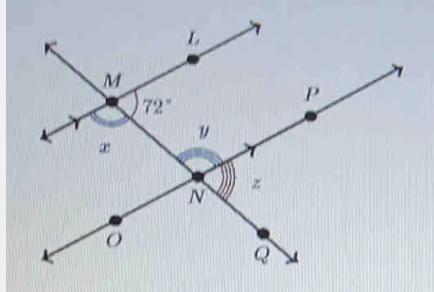
. ML is parallel to NP.
m/LMN = 72°
Gabriel was asked to find the measure of Zz and explain his reasoning.
M
.
Т
O
72°
L
N
2
P
Gabriel used the following theorem: When a transversal crosses parallel lines, alternate interior
angles are congruent.
Fill in the blanks in Gabriel's solution.
. Since ZLMN and Læ are a linear pair, m/x =
. Since Zx and Zy are alternate interior angles, m/y =
Since Zy and Zz are a linear pair, mZz
=
Answers
Two linear pairs are angles that form a ray when it is cut by a transversal line, and they are supplementary, meaning that the sum of their measures is of 180º.
Hence the measure of angle x is given as follows:
72 + x = 180
x = 180 - 72
x = 108º.
What are alternate interior angles?Alternate interior angles are between the two parallel lines, and on opposite sides of the transversal line, hence they are congruent, meaning that they have the same angle measure.
Thus the measure of angle y is given as follows:
m < y = 108º.
Since y and z are a linear pair, which we already studied the concept, the measure of angle z is given as follows:
m < y + m < z = 180
108 + m < z = 180
m < z = 72º.
Missing InformationThe diagram is given by the image shown at the end of the answer.
More can be learned about angle measures at https://brainly.com/question/25716982
#SPJ1
2x18-5+15%5=32
Insert parentheses to make each equal true
Answers
Answer:
( 2×8) - [ ( 5 + 15 ) ÷ 5] = 32
Step-by-step explanation:
According to the scenario, computation of the given data are as follows,
Given equation = 2x18-5+15/5=32
First we multiply first two letters,
then ( 2 × 18) = 36
Now, we add 5 and 15 then divide it by 5,
So, ( 5 + 15 ) ÷ 5 = 20 ÷ 5 = 4
Now we subtract 4 from 36,
Then 36 - 4 = 32
Hence the correct parentheses = ( 2×8) - [ ( 5 + 15 ) ÷ 5] = 32
Given the pre-image coordinates (0, 5), (-3, 2), (4, -1) and transformed image coordinates (2, -5), (-1, -2), (6, 1), what is the coordinate transformation in function notation?
Answers
Given:
The pre-image coordinates (0, 5), (-3, 2), (4, -1) and transformed image coordinates (2, -5), (-1, -2), (6, 1).
Required:
We need to find the transformation in function notation.
Explanation:
Let (x,y) be the pre-image coordinate and (x',y') be the transformed image coordinates.
The transformation is
\((x,y)\rightarrow(x^{\prime},y^{\prime}).\)Consider the points (0,5) and (2,-5).
Substitute the values in the transformation.
\((0,5)\rightarrow(2,-5)\)\((0,5)\rightarrow(0+2,-(5))\)Let x =0 and y =5, we get
\((x,y)\rightarrow(x+2,-y)\)Consider the points (-3,2) and (-1,-2).
\((-3,2)\rightarrow(-1,-2)\)\(Use\text{ }-3+2=-1.\)\((-3,2)\rightarrow(-3+2,-(2))\)Let x =-3 and y=2.
\((x,y)\rightarrow(x+2,-y)\)Consider the points (4,-1) and (6,-1).
\((4,-1)\rightarrow(6,1)\)\(Use\text{ }4+2=6.\)\((4,-1)\rightarrow(4+1,-(1))\)\((x,y)\rightarrow(x+2,-y)\)\(f(x,y)=(x+2,-y)\)Final answer:
\((x,y)\rightarrow(x+2,-y)\)\(f:(x,y)\rightarrow(x+2,-y)\)Researchers in a certain country investigated how having daughters influences voting o women's issues by members of the federal government. The researchers use voting records of each member of the federal government to compute an index score, where higher scores indicate more favorable voting for women's rights. The researchers model the index score (y) as a function of the number of daughters ( x ) a voting member has. Data collected for the 445 members of the federal government last year were used to fit the straight-line model, E(y)=β0+β1x. Complete parts a through c below. a. If it is true that having daughters influences voting on women's issues, will the sign of β1 be positive or negative? Explain. Positive, because if the claim is true, then index score would increase as the number of daughters increases. b. The following statistics were reported in the article: β^1=0.46 and sβ1=0.43. Find a 95% confidence interval for β1. A 95% confidence interval is (Round to three decimal places as needed.)
Answers
Researchers in a certain country investigated how having daughters influences voting o women's issues by members of the federal government: The 95% confidence interval for β1 is (0.046, 0.874).
To find the 95% confidence interval for β1, we use the formula:
β1 ± t * sβ1,
where β1 is the estimated coefficient, sβ1 is the standard error of β1, and t is the critical value from the t-distribution with degrees of freedom equal to the sample size minus the number of predictors.
In this case, the reported values are:
β^1 = 0.46 (estimated coefficient)
sβ1 = 0.43 (standard error of β1)
The sample size (n) is not given, so we cannot calculate the exact value of t. However, we can assume that the sample size is large enough to use the normal distribution approximation, which corresponds to a z-value for the 95% confidence level.
Using the z-value for a 95% confidence level (which is approximately 1.96), the confidence interval can be calculated as:
0.46 ± 1.96 * 0.43 = (0.046, 0.874).
Therefore, we can say with 95% confidence that the true value of β1 lies within the interval (0.046, 0.874).
To know more about confidence interval, refer here:
https://brainly.com/question/32546207#
#SPJ11
Consider the PDE au(x, t) = 4 d²u(x, t) 2 Ət əx² For each of BCs and ICs, solve the initial value problem. du(π,t) a) BCs: u(0,t)=0 = = 0 and əx IC: u(x,0) = x ANSWER: f(x)= n=1 u(2,t) = 0 and u(0,t)=0 u(x,0)=sin x ANSWER: f(x)=¹1_sin(2 + nx) na n=1 1+ 2 X b) BCs: IC: 8 (2n-1) T n+1 (-1)041 -4(2n-1)²t sin(2-nπ) nπ 1- 2 e sin (2n-1) 2 na sin X 2 -(nn)²t x -X
Answers
the solution for the initial value problem is: u(x, t) = sin(sqrt(-λ² * (a / 4)) * x) * exp(-λ² * t) where λ = ± sqrt(-4n² / a), and n is a non-zero integer.
The given partial differential equation is:
au(x, t) = 4 * (d²u(x, t) / dt²) / (dx²)
a) BCs (Boundary Conditions):
We have u(0, t) = 0 and u(π, t) = 0.
IC (Initial Condition):
We have u(x, 0) = x.
To solve this initial value problem, we need to find a function f(x) that satisfies the given boundary conditions and initial condition.
The solution for f(x) can be found using the method of separation of variables. Assuming u(x, t) = X(x) * T(t), we can rewrite the equation as:
X(x) * T'(t) = 4 * X''(x) * T(t) / a
Dividing both sides by X(x) * T(t) gives:
T'(t) / T(t) = 4 * X''(x) / (a * X(x))
Since the left side only depends on t and the right side only depends on x, both sides must be equal to a constant value, which we'll call -λ².
T'(t) / T(t) = -λ²
X''(x) / X(x) = -λ² * (a / 4)
Solving the first equation gives T(t) = C1 * exp(-λ² * t), where C1 is a constant.
Solving the second equation gives X(x) = C2 * sin(sqrt(-λ² * (a / 4)) * x) + C3 * cos(sqrt(-λ² * (a / 4)) * x), where C2 and C3 are constants.
Now, applying the boundary conditions:
1) u(0, t) = 0:
Plugging in x = 0 into the solution X(x) gives C3 * cos(0) = 0, which implies C3 = 0.
2) u(π, t) = 0:
Plugging in x = π into the solution X(x) gives C2 * sin(sqrt(-λ² * (a / 4)) * π) = 0. To satisfy this condition, we need the sine term to be zero, which means sqrt(-λ² * (a / 4)) * π = n * π, where n is an integer. Solving for λ, we get λ = ± sqrt(-4n² / a), where n is a non-zero integer.
Now, let's find the expression for u(x, t) using the initial condition:
u(x, 0) = X(x) * T(0) = x
Plugging in t = 0 and X(x) = C2 * sin(sqrt(-λ² * (a / 4)) * x) into the equation above, we get:
C2 * sin(sqrt(-λ² * (a / 4)) * x) * C1 = x
This implies C2 * C1 = 1, so we can choose C1 = 1 and C2 = 1.
Therefore, the solution for the initial value problem is:
u(x, t) = sin(sqrt(-λ² * (a / 4)) * x) * exp(-λ² * t)
where λ = ± sqrt(-4n² / a), and n is a non-zero integer.
Note: Please double-check the provided equation and ensure the values of a and the given boundary conditions are correctly represented in the equation.
To know more about Equation related question visit:
https://brainly.com/question/29657983
#SPJ11
Which equation could represent a linear combination of the system?
Answers
The equation that could represent a linear combination of the system 2/3x + 5/2y = 15 and 4x + 15y = 12 is 0 = 26
What are linear equations?Linear equations are equations that have constant average rates of change, slope or gradient
How to determine the linear combination to the system?A system of linear equations is a collection of at least two linear equations.
In this case, the system of equations is given as
2/3x + 5/2y = 15
4x + 15y = 12
Multiply the first equation by 6, to eliminate the fractions.
6 * (2/3x + 5/2y = 15)
This gives
4x + 15y = 90
Subtract the equation 4x + 15y = 90 from 4x + 15y = 12
4x - 4x + 15y - 15y = 12 - 90
Evaluate the difference
0 + 0 = -78
Evaluate the sum
0 = -78
The above equation is the same equation as option (b) 0 = 26
This is so because they both represent that the system of equations have no solution
Hence, the equation that could represent a linear combination of the system is 0 = 26
Read more about system of linear equations at
https://brainly.com/question/14323743
#SPJ1
Complete question
The system of equations below has no solution.
2/3x + 5/2y = 15
4x + 15y = 12
Which equation could represent a linear combination of the system?
helloooo I need this simplified, also please show work cause id.k how to do this :)
\(\frac{7\sqrt{10x} }{\sqrt{6} }\)
Answers
Answer:7√(10x)×√6/(√6×√6)=7/6×√60x
Step-by-step explanation:
Find the designated sum of the arithmetic series.
S9 of 22+20+18+16+…
Answers
Answer:
126
Step-by-step explanation:
a = 22
d = 22- 20 = -2
n = 9
Sn = 0.5n(2a +d(n-1))
=0.5 * 9 (2 *22 +-2(9-1))
= 126
Find an equation of the ellipse having a major axis of length 10 and foci at (1, 5) and (1, 1).
Answers
The equation of the ellipse having a major axis of length 10 and foci at (1, 5) and (1, 1) is (x - 1)²/100 + (y - 3)²/16 = 1. So, the correct answer is option B.
The equation of an ellipse is given by (x-h)²/a² + (y-k)²/b² = 1, where (h, k) is the center of the ellipse and a and b are the length of the major and minor axes respectively.
Since the major axis of the given ellipse has a length of 10, we can set a = 10. The two foci of the ellipse are given as (1, 5) and (1, 1) which means the center of the ellipse is the midpoint of these two foci, i.e., (1, 3). Therefore, h = 1 and k = 3.
We also need to calculate the length of the minor axis, b. We can calculate this value using the distance formula,
d = √((x2 - x1)² + (y2 - y1)²)
Therefore,
b = √((12 - 12)² + (52 - 12)²)
= √(0 + 16)
= 4
Therefore, the equation of the ellipse with a major axis on length 10 contains foci at (1, 5) and (1, 1) is given by (x - 1)²/100 + (y - 3)²/16 = 1.
To learn more about ellipse visit:
https://brainly.com/question/9702250
#SPJ4
Complete Question:
Find an equation of the ellipse having a major axis of length 10 with foci at (1, 5) and (1, 1):
A. (x - 1)²/100 + (y - 3)²/4 = 1
B. (x - 1)²/100 + (y - 3)²/16 = 1
C. (x - 1)²/25 + (y - 3)²/4 = 1
D. (x - 1)²/25 + (y - 3)²/16 = 1
A cost estimator for a construction company has collected the data found in the file Dat9-21.xlsx describing the total cost (Y) of 97 different projects and the following 5 independent variables thought to exert relevant influence on the total cost: regular or premium wages paid (X1), total units of work required (X2), contracted units of work per day (X3), level of equipment required (X4), and city/location of work (X5). The cost estimator would like to develop a regression model to predict the total cost of a project as a function of these 5 independent variables.
a. Prepare five scatter plots showing the relationship between the total cost of the projects and each of the independent variables. What sort of relationship does each plot suggest?
b. Which combination of the independent variables would you suggest the estimator use? What is the estimated regression equation for this model and what is its adjusted R2 value?
c. Suppose the estimator wants to use total units of work (X2) and city/location of work (X5) as the only independent variables for the regression model to predict total cost. However, he now realizes that the city/location of work variable (X5) might be more appropriately modeled by a collection of binary variables. Modify the data set to include the necessary binary variables. Because there are six distinct city/location values, five binary variables would be needed. Assume city/ location 6 should be represented by values of zero for all the binary variables.
d. Which combination of the new set of six independent variables (that is, X2 plus the five binary variables representing X5) would you now suggest the estimator use? What is the estimated regression equation for this model, and what is its adjusted R2 value?
e. Of the regression models identified in parts b and d, which would you recommend the cost estimator use and why?
Answers
To prepare scatter plots showing the relationship between the total cost of the projects and each of the independent variables, we can use the data from the file Dat9-21.xlsx.
Here are the scatter plots for each independent variable:
What is a Scatter plot?
A scatter plot is a type of data visualization that displays the relationship between two variables. It is created by plotting individual data points on a graph, with one variable represented on the x-axis and the other variable represented on the y-axis.
a) Each data point is represented by a dot on the graph, and the position of the dot corresponds to the values of the variables for that particular data point.
Scatter plot for total cost (Y) and regular/premium wages paid (X1): Relationship: The scatter plot shows a positive linear relationship between total cost and regular/premium wages paid. As the wages paid increase, the total cost tends to increase as well.
Scatter plot for total cost (Y) and total units of work required (X2):
Relationship: The scatter plot shows a positive linear relationship between total cost and total units of work required. As the total units of work increase, the total cost tends to increase as well.
Scatter plot for total cost (Y) and contracted units of work per day (X3):
Relationship: The scatter plot shows a positive linear relationship between total cost and contracted units of work per day. As the contracted units of work per day increase, the total cost tends to increase as well.
Scatter plot for total cost (Y) and level of equipment required (X4):
Relationship: The scatter plot does not show a clear linear relationship between total cost and the level of equipment required. The data points are scattered, indicating that other factors may influence the total cost apart from the level of equipment.
Scatter plot for total cost (Y) and city/location of work (X5):
Relationship: The scatter plot does not show a clear linear relationship between total cost and city/location of work. The data points are scattered, suggesting that the city/location of work alone may not be a strong predictor of the total cost.
b.) Based on the scatter plots and considering the relationship between the independent variables and the total cost, the estimator should consider using the combination of the following independent variables:
regular or premium wages paid (X1), total units of work required (X2), and contracted units of work per day (X3). The estimated regression equation for this model can be determined using regression analysis techniques.
c.) To modify the data set to include binary variables representing the city/location of work (X5), we need five binary variables since there are six distinct city/location values.
Let's assume the binary variables are represented as follows:
Binary variable X51: 1 if city/location is 1, 0 otherwise.
Binary variable X52: 1 if city/location is 2, 0 otherwise.
Binary variable X53: 1 if city/location is 3, 0 otherwise.
Binary variable X54: 1 if city/location is 4, 0 otherwise.
Binary variable X55: 1 if city/location is 5, 0 otherwise.
Binary variable X56: 1 if city/location is 6, 0 otherwise (all zeros).
d.) Based on the modified data set, the estimator should now consider using the combination of the following independent variables:
total units of work required (X2), binary variables X51, X52, X53, X54, and X55 representing the city/location of work. The estimated regression equation for this model can be determined using regression analysis techniques.
e.) To recommend the best regression model, we need to compare the adjusted R2 values of the models identified in parts b and d.
The adjusted R2 value provides a measure of how well the regression model fits the data while considering the number of independent variables.
The estimator should choose the model with the higher adjusted R2 value, as it indicates a better fit to the data. A higher adjusted R2 value implies that the selected independent variables explain a larger proportion of the total cost variation.
To learn more about regression model follow the given link:
https://brainly.com/question/30401933
#SPJ4
How much money will Shawn have in the bank after 5 years if he invests $1000 at a rate of 3% compounded quarterly? Which equation represents the situation?

Answers
The future value that Shawn will have in the bank after 5 years of investing $1,000 at a rate of 3% compounded quarterly is $1,161.18.
The equation that represents the situation is B) A = 1,000 (1.0075)⁴ˣ⁵
What is the future value?The future value describes the compounded present value at an interest rate.
The future value can be determined using the above FV formula or equation or an online finance calculator as follows:
N (# of periods) = 20 quarters (5 years x 4)
I/Y (Interest per year) = 3%
PV (Present Value) = $1,000
PMT (Periodic Payment) = $0
Results:
Future Value (FV) = $1,161.18
Total Interest = $161.18
Learn more about the future value at https://brainly.com/question/24703884.
#SPJ1
Find the measure of angle x in the figure below: triangle with 65 degrees in both bottom corners
Answers
Answer:
According to the "Triangle TheOrem", a triangles interior angles are always a 180°.
Therefore, to find the last remaining angle of the triangle, you will have to find the measure of the bottom angles (65° + 65° = 130°) THEN subtract 180° by 130°
65° + 65° = 130° (measures of the two bottom angles)
180° - 130° (to find the remaining angle!) = 50°
ANSWER = 50°
Hope I helped! ^^
-4^2-17×-4-76 pleaseeee helppppp
Answers
Answer:
-24
Step-by-step explanation:
it was hard but i got it first i did the the times and the
Answer:
8
Step-by-step explanation:
Use PEDMAS.
(-4)² - 17*(-4) - 76 = 16 - 17*(-4) - 76 {Exponents}
= 16 + 68 - 76 {Multiplication}
= 84 - 76 {Addition}
= 8 {Subtraction}
determine the measure of each angle. 4x - 90= ? Degree
Answers
Answer:
4x - 90= 90
Explain:
Simplifying
(4x + -90) = 90
Reorder the terms:
(-90 + 4x) = 90
Remove parenthesis around (-90 + 4x)
-90 + 4x = 90
Solving
-90 + 4x = 90
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '90' to each side of the equation.
-90 + 90 + 4x = 90 + 90
Combine like terms: -90 + 90 = 0
0 + 4x = 90 + 90
4x = 90 + 90
Combine like terms: 90 + 90 = 180
4x = 180
Divide each side by '4'.
x = 45
Simplifying
x = 45
Lashonda does a weekly exercise program consisting of cardiovascular work and weight training. Each week, she exercises for at least 7 hours. She spends at most 5 hours on weight training. She spends at most 11 hours doing cardiovascular work. Let × denote the time (in hours) that Lashonda spends doing cardiovascular work. Let y denote the time (in hours) that she spends on weight training. Shade the region corresponding to all values of x and y that satisfy these requirements.
Answers
The region (labelled A) corresponding to all values of x and y that is added as an attachment
How to determine the regionBased on the given information, we can write the following system of inequalities:
Lashonda exercises for at least 7 hours:
x + y ≥ 7
She spends at most 5 hours on weight training:
y ≤ 5
She spends at most 11 hours doing cardiovascular work:
x ≤ 11
So the system of inequalities can be written as:
x + y ≥ 7
y ≤ 5
x ≤ 11
Read more about inequalities at
https://brainly.com/question/30728087
#SPJ1

Find the volume of the cone.
either enter an exact answer in terms of π or use 3.14 for π and round your final answer to the nearest hundredth.

Answers
Answer:
18.84
Step-by-step explanation:
1. The formula for volume of a cone is (r^2x3.14xh)/3
2. So it would be 3^2x3.14x2 divided by 3
3. that would be 18.84
Mila reads at a rate of 3 paragraphs per minute.
After reading for 4 minutes, she had read a total of 12 paragraphs.
This situation can be represented with a linear equation written in point-slope form,
where x represents the number of minutes and y represents the number of
paragraphs
Use this information to complete each statement about the linear equation.
CL
The slope of the linear equation is
Answers
Answer:
Y=3x because that slope is 3 and if you times it by 4 you get 12
Step-by-step explanation:
20 people ride the bus, 80 people ride motorbikes, 65 people drive vans, and 215 people drive cars. Based on the data, how many would you expect to use motorbikes if you asked 800 people? how many people ride motorbikes
Answers
Given the diagram classify the bolded line as a perpendicular bisect or angle bisect or median or altitude write your answer on the line
Answers
Answer:
altitude
Step-by-step explanation:
It cant be a perpendicular bisector because its not splitting the triangle into equal lengths.

What does n equal in 6(2n – 3) – 2(6n + 1) = 10n?.
Answers
Answer:
n = -2
Step-by-step explanation:
6(2n - 3) - 2(6n + 1) = 10n
multiply the brackets
6*2n - 6*3 - 2*6n - 2*1 = 10n
12n - 18 - 12n - 2 = 10n
add or subtract the like terms
0 - 20 = 10n
shift 10 to the right hand side .REmember when u shift multiplication changes to division.
-20 / 10 = n
-2 = n
Answer:n=-2
Step-by-step explanation:
12n-18-12n-2=10n
-20=10n
n=-2
Nicole had two days to write a paper for her english class. She wrote 3 5/7 the first day and 4 1/2 pages the second day. How many total pages did nicole write for her paper.
Answers
Answer:
8 3/14 total pages
Step-by-step explanation:
3 + 4 = 7
5/7 + 1/2 = 10/14 + 7/14 = 17/14 = 1 3/14
7 + 1 3/14 = 8 3/14
Question 5 of 10
Which pair of functions are inverses of each other?
O A. f(x) = 2 + 15 and g(x) = 12x - 15
O B. f(x) = √3x and g(x) = () ³
O c. f(x) = 3 - 10 and g(x) = +10
3
D. f(x) = 11x-4 and g(x) = +4

Answers
The correct answer is D. f(x) = 11x - 4 and g(x) = (x + 4)/11
To determine which pair of functions are inverses of each other, we need to check if the composition of the functions results in the identity function, which is f(g(x)) = x and g(f(x)) = x.
Let's test each option:
Option A:
f(x) = x/2 + 15
g(x) = 12x - 15
f(g(x)) = (12x - 15)/2 + 15 = 6x - 7.5 + 15 = 6x + 7.5 ≠ x
g(f(x)) = 12(x/2 + 15) - 15 = 6x + 180 - 15 = 6x + 165 ≠ x
Option B:
f(x) = ∛3x
g(x) = (x/3)^3 = x^3/27
f(g(x)) = ∛3(x^3/27) = ∛(x^3/9) = x/∛9 ≠ x
g(f(x)) = (∛3x/3)^3 = (x/3)^3 = x^3/27 = x/27 ≠ x
Option C:
f(x) = 3/x - 10
g(x) = (x + 10)/3
f(g(x)) = 3/((x + 10)/3) - 10 = 9/(x + 10) - 10 = 9/(x + 10) - 10(x + 10)/(x + 10) = (9 - 10(x + 10))/(x + 10) ≠ x
g(f(x)) = (3/x - 10 + 10)/3 = 3/x ≠ x
Option D:
f(x) = 11x - 4
g(x) = (x + 4)/11
f(g(x)) = 11((x + 4)/11) - 4 = x + 4 - 4 = x ≠ x
g(f(x)) = ((11x - 4) + 4)/11 = 11x/11 = x
Based on the calculations, only Option D, where f(x) = 11x - 4 and g(x) = (x + 4)/11, satisfies the condition for being inverses of each other. Therefore, the correct answer is:
D. f(x) = 11x - 4 and g(x) = (x + 4)/11
for such more question on inverses
https://brainly.com/question/15066392
#SPJ8
