HELP ASAP!!!
Solve for m in the following equation.
4m/3= 8
m= 10
m= 6
m= 2
m= 96
You buy three more than twice as many pounds of apples as bananas. If you bought seven pounds of apples, how many pounds of bananas did you buy?
What is the correct equation and solution for this problem?
3p – 2 = 7; p = 3 pounds
2p – 3 = 7; p = 5 pounds
3p + 2 = 7; p = 3 pounds
2p + 3 = 7; p = 2 pounds
Thank you!!
Answers
I hope you get it right… please like :)
Answer:
1. STEPS FOR SOLVING LINEAR EQUATION
\( \frac{4m}{3} = 8\)
Multiply both sides by 3.
4m=8×3
Multiply 8 and 3 to get 24.
4m=24
Divide both sides by 4.
\(m = \frac{24}{4} \)
Divide 24 by 4 to get 6.
m=6
2. 2p+3=7; p=2 pounds
Related Questions
En una compañía se realiza una encuesta a 200 personas, se encontró la siguiente distribución, en el uso de máquinas eléctricas, mecánicas y computadoras: Eléctricas 110, mecánicas 50, computadoras 60. Mecánicas y computadoras 25, eléctricas y computadoras 35, eléctricas y mecánicas 40. Las tres 20 y 60 nada. A) Encuentre el número de personas que o usan computadora. B) Que usen una maquina eléctrica pero no computadora. C) Que usen solo un equipo. D) Que usen mecánica y eléctrica pero no computadora. E) Cuantos no tienen ni maquina eléctrica ni mecánica.
Answers
Answer:
A) 140
B) 75
C) 80
D) 20
E) 80
Step-by-step explanation:
Para resolver este problema debemos construir un diabrama de Venn y llenarlo según los datos que se nos brindan.
Comenzamos nombrando cada círculo:
E= personas que usan máquinas eléctricas
M= personas que usan máquinas mecánicas
C = personas que usan computadoras.
- Luego llenamos el área central con un 20, el cual representa las personas que usan los 3 tipos de maquinas.
- En la parte exterior del diagrama de Venn colocamos un 60 por las personas que no usan ninguna de las máquinas.
- En la intersección entre M y C restamos:
25-20=5
Entonces colocamos este 5 en esa región.
- En la intersección entre E y C restamos:
35-20=15
Entonces colocamos este 15 en esa región.
- En la intersección entre E y M restamos:
40-20=20
Entonces colocamos este 20 en esa región.
- En la región de E restamos:
110-20-20-15=55
Entonces colocamos este 55 en esa región.
- En la región de M restamos:
50-20-20-5=5
Entonces colocamos este 5 en esa región.
- En la región de C restamos:
60-15-20-5=20
Entonces colocamos este 20 en esa región.
Y obtenemos el diagrama de Venn que representa esta encuesta (Ver figura adjunta)
Y ahora ya lo podemos usar para responder a las preguntas:
A) Número de personas que no usan computadora. Sumamos los números fuera del círculo C:
55+20+5+60=140
B) Número de personas que usan una máquina eléctrica pero no computadora: Sumamos los números dentro del círculo E con excepción de los números compartidos por el círculo C y obtenemos:
55+20=75
C) Número de personas que usan solo un equipo: Sumamos los números no compartidos en los círculos E, M y C
55+20+5=80
D) Número de personas que usan máquina mecánica y eléctrica pero no computadora: Usamos el número compartido entre E y M que no son compartidos con C
20
E) Sumamos el número que se encuentra solo en C y los que están afuera del diagrama:
20´60=80

a marketing student is estimating the average amount of money that students at a large university spent on sporting events last year. he asks a random sample of 50 students at one of the university football games how much they spent on sporting events last year. using this data he computes a 90% confidence interval, which turns out to be ($217, $677).which one of the following conclusions is valid?which one of the following conclusions is valid?use the t-distribution inverse calculator applet to answer the following question.what is the 95% confidence interval for the number of hours students in their college study?
Answers
The valid conclusion is A. We can be 90% ... the mean amount ... is between $217 and $677.
The confidence interval used by the student researcher refers to the probability that the university's population parameter (average amount that students spent on sporting events last year) will fall between $217 and $677 for 90% of the time.
A confidence interval is the mean of your estimate plus and minus the variation in that estimate. This is the range of values you expect your estimate to fall between if you redo your test, within a certain level of confidence. Confidence, in statistics, is another way to describe probability.
Thus, the interval measurement gives the researcher some degree of certainty that the calculated sample mean falls within the population mean most of the time.
Learn more about confidence interval here :-
https://brainly.com/question/24131141
#SPJ4
The complete question is:-
marketing student is estimating the average amount of money that students at a large university spent on sporting events last year. He asks a random sample of 50 students at one of the university football games how much they spent on sporting events last year. Using this data he computes a 90% confidence interval, which turns out to be ($217, $677). Which one of the following conclusions is valid? We can be 90% confident that the mean amount of money spent at sporting events last year by all the students at this university is between $217 and $677. 90% of the sample said they spent between $217 and $677 at sporting events last year. No conclusion can be drawn.
Can’t figure this one out

Answers
8.4x-5=20.2 solve for x
Answers
Answer:
x=3
Step-by-step explanation:
1. Craig borrowed $1,200 from his parents to buy a stereo. His parents charged him 5% simple interest for 3 years. How much interest did he pay his parents?
Answers
Work:
I=PRT
I=?
P= 1200 X%I=PxRxT =250; 250R105=I
R=0.05
T=3
Find two numbers whose sum is 49. If the greater is 4 more than 8 times the smaller. Solve
Answers
I got
44
and
5
Explanation:
Call the numbers
x
and
y
, you get:
x
+
y
=
49
x
=
8
y
+
4
substitute the second equation into the first:
8
y
+
4
+
y
=
49
9
y
=
45
y
=
45
9
=
5
so that:
x
=
8
⋅
5
+
4
=
44
Answer:
5 and 44
Step-by-step explanation:
smaller number: x
greater number: 8x + 4
x + 8x + 4 = 49
9x + 4 = 49
9x = 45
x = 5
smaller number: 5
greater number: ?
8(5) + 4 = 40 + 4 = 44
5 + 44 = 49
Hope that helps.
PART 2:
The regular price, in dollars, the gym charges can be represented by the equation y=15x+20
B.How much money, in dollars, does justin save the first month by joining the gym at the discounted price rather than at the regular price?
Answers
The amount of money Justin saves in the first month would be 5 times the value of x, where x represents the number of months of gym membership, based on the discounted price provided.
What is the linear equation?A linear equation is an equation in mathematics that represents a relationship between two variables that is a straight line when graphed on a coordinate plane. It is an equation of the form:
y = mx + b
To calculate the amount of money Justin saves in the first month by joining the gym at the discounted price rather than the regular price, we need to know the discounted price.
The equation given is y = 15x + 20, where y represents the regular price in dollars and x represents the number of months of gym membership. However, we need to know the discounted price, which is not provided in the given information.
Once we have the discounted price, we can substitute it into the equation and calculate the savings. For example, if the discounted price is y = 10x + 20, then we can calculate the savings by subtracting the discounted price from the regular price:
Savings = Regular price - Discounted price
= (15x + 20) - (10x + 20)
= 15x - 10x
= 5x
Hence, the amount of money Justin saves in the first month would be 5 times the value of x, where x represents the number of months of gym membership, based on the discounted price provided.
To learn more about linear equation, Visit
brainly.com/question/2030026
#SPJ1
hii please help I'm super confused !

Answers
Answer:
Below
Step-by-step explanation:
Two points are given....calculate the slope, m = (y1-y2) / (x1-x2)
= ( 3-1) / ( 0 - - 8) = 2/8 = 1/4
Only equation II has slope = 1/4
HELP! The function f is defined above. For what value of k, if any, is f continuous at x=-7
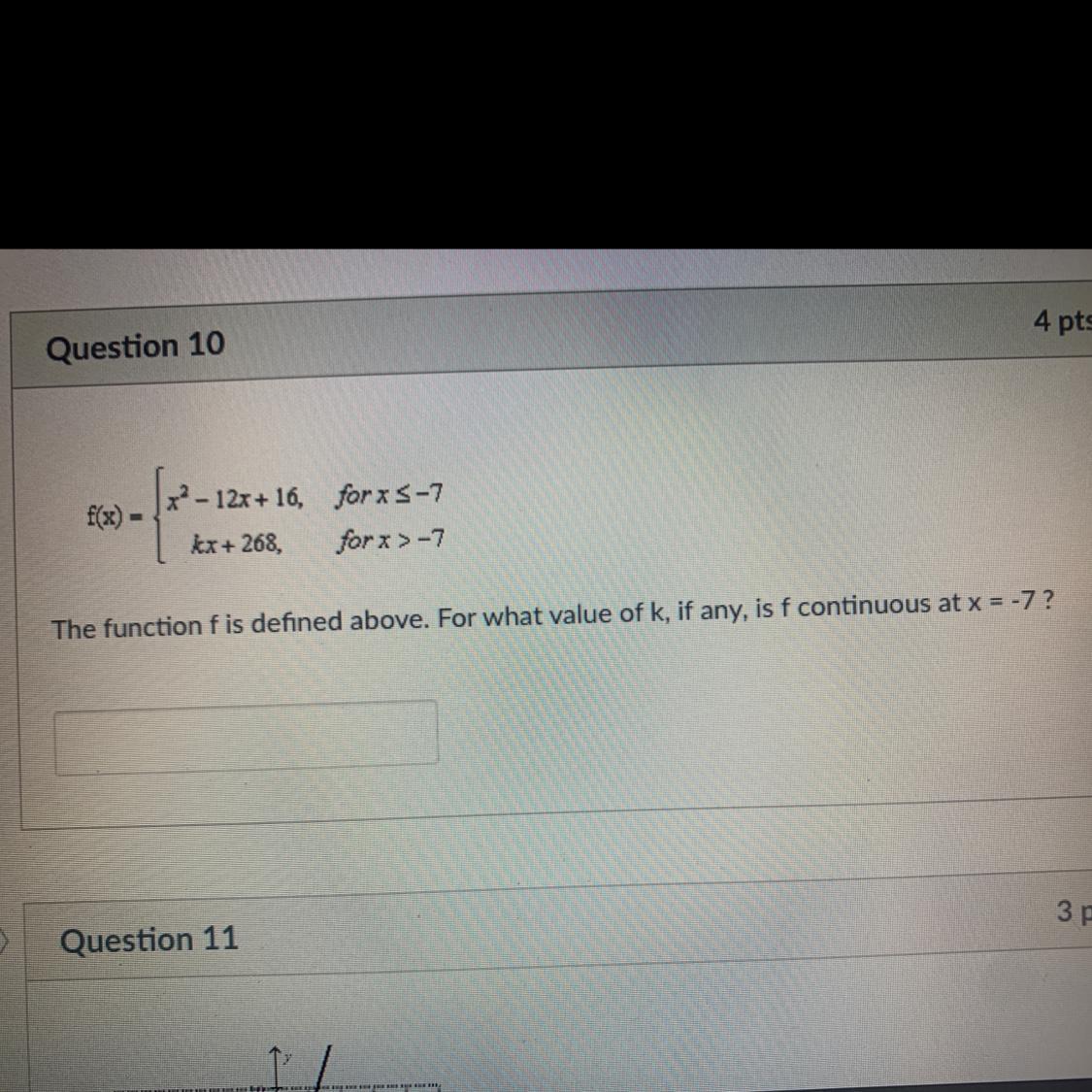
Answers
In order for the function to be continuous at x = -7, the limits from either side as x approaches -7 must be equal:
\(\displaystyle \lim_{x\to-7^-} f(x) = \lim_{x\to-7}(x^2-12x+16) = 149\)
\(\displaystyle \lim_{x\to-7^+} f(x) = \lim_{x\to-7}(kx+268) = -7k+268\)
Solve for k :
149 = -7k + 268
7k = 119
k = 17
The function f(x) is continuous at x = -7 if and only if k = 41. This is because for continuity to hold at x = -7, the value of k must be such that the left-hand limit, right-hand limit, and the actual value of the function at x = -7 are equal. In this case, the value of k that satisfies this condition is k = 41.
For a function to be continuous at a specific point, the following conditions must be satisfied:1. The function must be defined at that point (i.e., the function should have a value at x = -7).
2. The limit of the function as x approaches -7 from the left must be equal to the limit of the function as x approaches -7 from the right.
3. The value of the function at x = -7 must be equal to the limits mentioned in condition 2.
Let's go through each of these conditions step by step for the given function:
Given function:
f(x) = { \(x^2 - 12x + 16\), for x <= -7
kx + 268, for x > -7
1. The function must be defined at x = -7:The function is defined at x = -7 for the first part of the piecewise definition: x^2 - 12x + 16. So, this condition is satisfied.
2. The limit from the left must be equal to the limit from the right as x approaches -7:We need to calculate the limits as x approaches -7 from the left (LHL) and from the right (RHL) for the second part of the piecewise definition: kx + 268.
LHL as x approaches -7: lim (x->-7-) [kx + 268] = -7k + 268.
RHL as x approaches -7: lim (x->-7+) [kx + 268] = -7k + 268.
Since both the left-hand limit and the right-hand limit are equal (-7k + 268), this condition is satisfied.
3. The value of the function at x = -7 must be equal to the limits: \(f(-7) = -7^2 + 12 * 7 + 16 = 49 - 84 + 16 = -19.\)
The limits from conditions 2 are -7k + 268.
To have continuity, the value of the function at x = -7 must be equal to the limits: -19 = -7k + 268.
Solving for k: -7k = -19 - 268
-7k = -287
k = 41.
So, for the function f to be continuous at x = -7, the value of k must be 41.
To know more about continuous:
https://brainly.com/question/31523914
#SPJ3
what value of x makes 1/2 (3x+ 4) = 1/2 x true
Answers
The value of x which makes the given expression 1/2(3x+4) = 1/2x true is -2
We have to simplify the given expression to find the value of x
1/2(3x + 4) = 1/2x
Cancel 1/2 from both sides
⇒ 3x + 4 = x
⇒ 2x = -4
⇒ x = -2
Hence, the value of x is -2 which makes the given expression true.
Learn more about value here
https://brainly.com/question/4806080
#SPJ1
find the absolute maximum and absolute minimum (if any) of the given function on the specified interval. f (x)
Answers
The answer of the function found to be x = −4 and x = 2, with M = 38.
We must consider the function,
f (x) = x³ + 6x² + 6
Over the interval
-5 \(\leq\) x \(\leq\) 2
To obtain the extrema we start from the function's derivative.
f' (x) = 3x² + 12x
Equating it to 0,
f' (x) = 0 = 3x(x +4) = 0
We arrive at two solutions,
x1 = 0, x2 = -4 both inside the interval.
Evaluating the function at the stationary points,
f (x1) = 6
f (x2) = (-4)³ + 6 . (-4)² + 6 = -64 + 96 + 6 = 38
These values must be compared to that of the function at the interval frontiers,
f (-5) = (-5)³ + 6 . (-5)² + 6 = -125 + 150 + 6 = 31
f (2) = 2³ + 6 . 2² + 6 = 38
Comparing the results we can conclude that the function attains its absolute minimum at,
x = 0, m = 6
Meanwhile, the absolute maximum is attained at the points,
x = −4 and x = 2, with M = 38.
Learm more about maxima and minima here; https://brainly.com/question/82347
#SPJ4
4.1 Prove that the opposite sides in parallelogram ABCD are equal.

Answers
It has been proven that the opposite sides of the parallelogram ABCD are equal
How to prove a Parallelogram?We are told that ABCD is the parallelogram and AC is a diagonal. We observe that the diagonal AC divides parallelogram ABCD into two triangles, namely, ∆ABC and ∆CDA.
Thus, we have o first prove that these triangles are congruent.
In ∆ABC and ∆CDA, w note that BC || AD and AC is a transversal.
Thus, BCA = DAC (Pair of alternate angles)
And AC = CA (reflexive property of congruency)
So, ∆ABC and ∆CDA are congruent (ASA rule).
Therefore, the corresponding parts AB = CD and AD = BC
Hence proved.
Read more about Parallelogram proof at: https://brainly.com/question/30177531
#SPJ1
On a world map, the distance between city A and city B is 10.125 inches. The two cities are actually 3038 miles apart. On the same map, what would be the distance between city C and city D, two cities that are actually 3445 miles apart? Use a proportion to solve this problem.On the map, the distance between city C and city D is _____ inches.(Round to three decimal places as needed.)
Answers
We will use the proportional method to solve the question
Since the distance on the map of actual distance 3038 miles is 10.125 inches
Since we need to find the distance on the map of the actual distance of 3445 miles
Then by using the proportional method
\(\frac{10.125}{x}=\frac{3038}{3445}\)By using the cross-multiplication
\(\begin{gathered} x\times3038=10.125\times3445 \\ \\ 3038x=34880.625 \end{gathered}\)Divide both sides by 3038
\(\begin{gathered} \frac{3038x}{3038}=\frac{34880.625}{3038} \\ \\ x=11.481\text{ inches} \end{gathered}\)On the map, the distance between city C and city D is 11.481 inches
For anyone who had the similar question.

Answers
Express the location of the point on the number line as both a fraction and a decimal.

Answers
Fraction: 3/10
how much more is 9,908,345 than 452,189
Answers
find p(-1) p(1) if p(x) = X2+1
Answers
Answer:
p(- 1) = 2 and p(1) = 2
Step-by-step explanation:
Substitute x = - 1 and x = 1 into p(x), that is
p(- 1) = (- 1)² + 1 = 1 + 1 = 2
p(1) = 1² + 1 = 1 + 1 = 2
Idil has a smart phone data plan that costs $25 per month that includes 10 GB of
data, but will charge an extra $20 per GB over the included amount. How much
would Idil have to pay in a month where she used 4 GB over the limit? How much
would Idil have to pay in a month where she used went over by x GB?
Answers
If f(x) = 3x + 2, what is f(5)
Answers
Answer:
Step-by-step explanation:
17
Prove the following...

Answers
Answer:
\({ \rm{ \sqrt{ \frac{1 + \cos(x) }{1 - \cos(x) } } }} \\ \\ \)
- Rationalize the denominator of the above expression;
\({ \rm{ = \sqrt{ \frac{(1 + \cos(x)).(1 + \cos(x)) }{(1 - \cos(x)).(1 + \cos(x)) } } }} \\ \\ = { \rm \sqrt{ \frac{( {1}^{2} + 2 \cos(x) + \cos ^{2}(x)) }{( {1}^{2} - { \cos }^{2}(x)) } } } \\ \\ = { \rm\sqrt{ \frac{(1 + 2 \cos(x) + { \cos }^{2} (x)) }{(1 - { \cos }^{2}(x)) } } }\)
- From the above expression, 1 - cos²x = sin²x
\( = { \rm{ \sqrt{ \frac{1 + 2 \cos(x) + { \cos }^{2}(x) }{ { \sin }^{2}(x) } } }} \\ \)
\( = { \rm{ \sqrt{ \frac{ {(1 + \cos(x)) }^{2} }{ { \sin}^{2}x } } }} \\ \\ = { \rm{ \frac{ \sqrt{(1 + \cos(x)) {}^{2} } }{ \sqrt{ { \sin}^{2} x} } }} \\ \\ = { \rm{ \frac{1 + \cos(x) }{ \sin(x) } }} \\ \\ = { \rm{ \frac{1}{ \sin(x) } + \frac{ \cos(x) }{ \sin(x) } }} \\ \\ = { \boxed{ \rm{ \: \csc(x) + \cot(x) \: }}}\)
PART-B Answer any five Questions from Perform the required operation. Show your solution on the space provided. You may use the attached paper. (2 Marks) 6. Form the differential equation y = a e³ˣ + b e⁻³ˣ - 2x by eliminating the arbitrary constants a and b.
Answers
By differentiating the given equation, we can eliminate the arbitrary constants a and b and obtain the differential equation y'' - 6y' + 18y = -2.
To eliminate the arbitrary constants a and b from the given equation y = \(ae^{(3x)} + be^{(-3x)} - 2x\), we need to differentiate the equation with respect to x.
First, we differentiate y = \(ae^{(3x)} + be^{(-3x)} - 2x\) with respect to x, which gives\(y' = 3ae^{(3x)} - 3be^{(-3x)} - 2.\)
Next, we differentiate y' with respect to x to obtain \(y'' = 9ae^{(3x) }+ 9be^{(-3x)}\).
Substituting these derivatives into the original equation, we have:
\(9ae^{(3x)} + 9be^{(-3x)} - 6(3ae^{(3x)} - 3be^{(-3x) - 2)} + 18(ae^{(3x)} + be^{(-3x)} - 2x) = -2.\)
Simplifying the equation, we get:
\(9ae^{(3x)} + 9be^{(-3x)} - 18ae^{(3x)} + 18be^{(-3x)} + 18ae^{(3x)} + 18be^{(-3x)} - 36x = -2.\)
Cancelling out the terms, we have:
\(-6ae^{(3x)} - 6be^{(-3x)} - 36x = -2.\)
Dividing through by -6, we obtain the final differential equation:
y'' - 6y' + 18y = -2.
Therefore, by differentiating the given equation, we eliminate the arbitrary constants a and b and obtain the differential equation y'' - 6y' + 18y = -2.
Learn more about differential equation here:
https://brainly.com/question/32524608
#SPJ11
A company that ships crystal bowls claims that bowls arrive undamaged in 95 percent of the shipments. Let the random variable G represent the number of shipments with undamaged bowls in 25 randomly selected shipments. Random variable G follows a binomial distribution with a mean of 23.75 shipments and a standard deviation of approximately 1.09 shipments. Which of the following is the best interpretation of the mean?
i. Every shipment of 25 bowls will have 23.75 undamaged bowls
ii. Every shipment of 25 bowls will have 23.75 damaged bowls
iii. On average, the company receives 23.75 shipments before receiving the first shipment with a damaged bowl.
iv. For all possible shipments of 25, the average number of damaged shipments is equal to 23.75
v. For all possible shipments of size 25, the average number of undamaged shipments is equal to 23.75.
Answers
The best interpretation of the mean in this case is:
v. For all possible shipments of size 25, the average number of undamaged shipments is equal to 23.75.
The mean of a binomial distribution represents the average or expected value of the random variable. In this context, the random variable G represents the number of shipments with undamaged bowls in 25 randomly selected shipments. The mean of 23.75 suggests that, on average, out of all possible shipments of size 25, the company can expect to have approximately 23.75 shipments with undamaged bowls.
To know more about number visit;
brainly.com/question/3589540
#SPJ11
What is the result of subtracting the second equation from the first? \begin{aligned} 8x-4y &= -4 \\\\ -3x+4y &= 5 \end{aligned} 8x−4y −3x+4y =−4 =5
Answers
The resulting equation after the equations are subtracted is 11x - 8y = -9
How to determine the resulting equation after the subtraction?From the question, we have the following parameters that can be used in our computation:
8x-4y &= -4 \\\\ -3x+4y &= 5
Rewrite these equations properly
So, we have the following representations
8x-4y = -4
-3x+4y = 5
When the second equation is subtracted from the first, we have the following representation
8x + 3x - 4y - 4y = -4 - 5
Evaluate the like terms
So, we have
11x - 8y = -9
Hence. the solution is 11x - 8y = -9
Read more about equations at
https://brainly.com/question/2476251
#SPJ1
Bernard wants to give a book and a CD to Rachel for Rachel's birthday. Bernard has 2 books and 3 CDs. Tell whether the situation involves combinations or permutations. Then give the number of possible outcomes.
Answers
Answer:
6, permutation
Step-by-step explanation:
Book 1, CD 1
Book 1, CD 2
Book 1, CD 3
Book 2, CD 1
Book 2, CD 2
Book 2, CD 3
There are 6 permutations.
Complete the ratio 4:? = 1:15
Answers
Answer:
The answer is 60
Step-by-step explanation:
Solution:
Complete the ratio
\( \frac{4}{?} = \frac{1}{15} \\ \)
?= 15×4?=60Hope you understand
Alex rents a car for one day the charge is $28 plus $0.50 per mile Alex wants to spend exactly $30 how many miles can he drive
Answers
Answer:
4 milesStep-by-step explanation:
Let the miles is x:
28 + 0.5x = 300.5x = 30 - 280.5x = 2x = 2/0.5x = 4It seems incorrect but Alex can drive 4 miles
Please help! On a field trip, there are 3 chaperones for every 20 students. There are 92 people on the trip.
Part a: How many chaperones are there?
Part b: how many students are there?
Answers
Answer:
A: 12 B: 80
Step-by-step explanation:
92 - 80 = 12
80 students
12 Chaperones
Answer:
12 chaperones and 80 students
Step-by-step explanation:
Start by multiplying the numbers seperatly and then add. Keep doing this till you get to 92.
20(2)=40. 3(2)=6 46
20(3)=60. 3(3)=9 69
20(4)=80. 3(4)=12 92
Now you know there are 12 chaperones and 80 students. There are other ways to answer this problem like using systems of equations but it still gives the correct answer and is less advanced.
Hope this helps:)
Frances has $5 in her bank. She finds $0. 25 under her bed. Then she finds $0. 40 more in her pocket. How much money does Frances have in all?
Answers
Step-by-step explanation:
Add all the money
$5+ 0.25+ 0.40= $5.65
Tyler's mom purchased a savings bond for Tyler. The value of the savings bond increases by 5% each year. One year after it was purchased, the value of the savings bond was $131.25. Find the value of the bond when Tyler's mom purchased it. The value of the bond when his mom purchased it was? Enter only the numeric value, no symbols or spaces. $
.
Answers
Answer:
125
Step-by-step explanation:
131.25 105
of 100
Cross multiply process
131.25x100=108x?
131.25x100=13125
13125=108?
13125/108=?
125=?
:)
a patent is the exclusive right to a product for a period of enter your response here years from the date the patent is filed with the government. (enter your response as an integer.)
Answers
A patent is a form of intellectual property that gives an individual or organization the exclusive right to manufacture, use, and/or sell an invention for a set period of time.
The length of a patent varies by country, but generally lasts for 20 years from the date the patent is filed with the government. This period can be extended in certain cases if the patent office grants a patent term extension.
The formula for calculating the length of a patent is: Length of Patent = Initial 20 Year Period + Extension. The initial 20 year period starts from the filing date of the patent application and is the same for all countries. However, the length of the extension varies depending on the country and the circumstances of the patent. For example, some countries may offer a 5-year extension, while others may offer a 10-year extension.
The length of a patent must be carefully calculated so that the patent owner can maximize the benefits of the patent. By calculating the patent length and extension, the patent owner can ensure that they are able to take advantage of their exclusive right to the invention for the maximum amount of time possible.
Learn more about amount of time here:
https://brainly.com/question/24258354
#SPJ4