He finds that the mean is 79.0 and the median is 78.0
for these six quiz scores. If John earns a 100% on the
next exam, what will the new mean and median be?
The new mean will be 82.0 and the new median will
be 78.0.
O The new mean will be 82.0 and the new median will
be 80.0
The new mean will be 89.5 and the new median will
be 78.0.
The new mean will be 89.5 and the new median will
be 80.0
Answers
The correct answer is: The new mean will be 82.0 and the new median will be 78.0.
To determine the new mean and median after John earns a 100% on the next exam, we need to consider the impact of this score on the overall data.
Given that the mean is the average of all the scores, adding a perfect score of 100 will increase the total sum of scores. Since the mean is calculated by dividing the sum of scores by the number of scores, the new mean will be higher than the previous mean.
However, the median is the middle value when the scores are arranged in ascending order. Since the median only considers the middle value, adding a perfect score will not affect the median as long as it remains in the middle position.
Considering the given options, the correct answer would be:
The new mean will be 82.0 and the new median will be 78.0.
This is because the median will remain the same at 78.0 since the 100% score does not change the middle position. However, the new mean will increase due to the addition of the high score.
So, the correct answer is: The new mean will be 82.0 and the new median will be 78.0
Learn more about median here:
https://brainly.com/question/300591
#SPJ11
Related Questions
Choose the most apt description of expected value. The standard deviation of a random variable. The best result you can hope for in an experiment. The median of a random variable. What you should expect to happen in an experiment every time. The long-term average outcome of an experiment.
Answers
The most apt description of expected value is: The long-term average outcome of an experiment.
Expected value refers to the long-term average outcome of an experiment. It is a mathematical concept that represents the average value of a random variable over an infinite number of trials.
In other words, it is the sum of all possible outcomes of an experiment, weighted by their probability of occurring.
Expected value is a crucial concept in probability theory and statistics, as it helps in predicting the likely outcome of an experiment or event. It is often used in decision-making processes, such as in finance and insurance, to calculate the potential risks and rewards associated with different options.
The other options listed in the question are not correct definitions of expected value. The standard deviation is a measure of the variability or spread of a random variable, while the best result and median are specific values that may or may not be related to the expected value.
What you should expect to happen in an experiment every time may be related to the expected value, but it is not a precise definition.
Overall, expected value is a fundamental concept in probability theory and statistics that represents the long-term average outcome of an experiment or event.
To know more about expected value refer here:
https://brainly.com/question/28197299#
#SPJ11
What is the GCF of 288 and 15? The problem is 288 over 15 as a fraction to simplify.
Answers
Answer:
3
Step-by-step explanation:
Verify that both y_1(t) = 1 - t and y_2(t) = -t^2/4 are solutions of the initial value problem
Answers
Since y_1(0) = 1, it satisfies the initial condition. However, y_2(0) = 0 does not satisfy the initial condition, as it should be y(0) = 1. Therefore, only y_1(t) is a solution of the initial value problem.
To verify that both y_1(t) = 1 - t and y_2(t) = -t^2/4 are solutions of the initial value problem, we first need to understand what the problem is. An initial value problem is a differential equation that includes an initial condition. In this case, we can assume that the initial condition is y(0) = 1.
Now, let's substitute both y_1(t) and y_2(t) into the differential equation and see if they satisfy the initial condition. The differential equation is not provided, but assuming it is y'(t) = -t/2, we have:
y_1'(t) = -1
y_2'(t) = -t/2
Substituting y_1(t) and y_2(t) into the differential equation gives:
y_1'(t) = -1
= -t/2 (when t = 2)
y_2'(t) = -t/2
= -t/2 (for all t)
Thus, both y_1(t) and y_2(t) satisfy the differential equation. Now, let's check if they satisfy the initial condition.
y_1(0) = 1 - 0
= 1
y_2(0) = -0^2/4
= 0
In conclusion, y_1(t) = 1 - t is the only solution that satisfies the differential equation and initial condition, while y_2(t) = -t^2/4 is not a solution since it does not satisfy the initial condition.
To know more about initial value visit:
https://brainly.com/question/17613893
#SPJ11
7. Tyler works in a shoe store. Tyler earns a commission. He earns 3.5% of the amount he sells. Last
week, he sold $600 worth of shoes. How much was his commission?
Answers
His commission was: 21$
EXPLICATION:
He sold 600$ which presents 100% of his sells.
We have to find how much 3.5% of this amount.
100%—->600$
3.5%—->3.5x600/100=21$
Which measurement statement is correct 10 points
Answers
I really need help ASAP ILL GIVE BRAINLY

Answers
Answer: D.
Step-by-step explanation:
You can start out with the form AX = B and solve for matrix X that would yield the answer
Then X = (A^-1)(B)
A = [1 -1]
[1 1]
A^-1 = (1/(1 - (1)(-1)))*[1 1]
[-1 1]
which can be written as (1/2) * [1 1]
[-1 1]
B = [26]
[6]
(A^-1)(B) = (1/2)*[1 1] [6]
[-1 1] [26]
= (1/2)*[32]
[20]
= [16]
[10]
Type the correct answer in each box. Use numerals instead of words.
Harry buys a boat in 2010. He plans on selling it in 2020. In 2010, the boat costs $20,000. The value of the boat depreciates over time
as is shown in the graph below, where the y-axis represents the value of the boat, in dollars, and the x-axis represents the number of
years since 2010.

Answers
Answer:
The initial value of the boat was $20,000
The percent decrease per year of the value of the boat is 10%.
The interval on which the value of the boat is decreasing while Harry has it is (0,10)
Step-by-step explanation:
It is given that the boat costs $20,000 in 2010 when x = 0. So, the initial value of the boat was $20,000.
Next, find the percent decrease per year of the value of the boat. Consider the general form of an exponential equation, y = a(b)x, where a is the initial value of the boat, b is the base of the exponent, x is the number of years after 2010, and y is the value of the boat, in dollars.
Consider the point (1 , 18,000) which lies on the graph of this situation. Substitute x = 1, y = 18,000, and a = 20,000 into the exponential equation and isolate b.
Recall that for exponential decay, b = 1 - r where r represents the decay rate. Substitute b = 0.9 into this equation and solve for r.
So, the decay rate is 0.1, and the percent decrease per year of the value of the boat is 10%.
Harry bought the boat in 2010, and plans on selling it after 10 years in 2020. Therefore, the interval on which the value of the boat is decreasing while Harry has it is [0, 10].
a
b
c
whuch is the answer look at the picture
d

Answers
Answer:
Step-by-step explanation:

Evaluate: 5x + 3 for when x = 2
Answers
Answer:
13
Step-by-step explanation:
5 · x + 3 = 5 · 2 + 3 = 10 + 3 = 13
h(x) = x2 + 3. Is frl a function and why/why not?
No, the inverse function does not pass the horizontal line test.
No, the inverse function does not pass the vertical line test.
Yes, the inverse function has one y-value for every x-value.
Yes, the inverse function has one x-value for every y-value.
Answers
is good answer the x value and y value
Answer:
No, the inverse function does not pass the horizontal line test.
Step-by-step explanation:
HELP PLEZ!!
expand and simplify:
2(3x-5)+ 3(2x+3)
Answers
Answer:
The answer is 11x - 1
Step-by-step explanation:
I did the distributive property and it should look like this 6x - 10 + 5x + 9
After that I just combined like terms and got 11x - 1
pls mark brainliest
Answer:
2(3x - 5) + 3 (2x + 3)
6x - 10 + 6x + 9
6x - 1 + 6x
12x -1
Step-by-step explanation:
Hope this helps!!
True or false 6 to the 3 power = 216
Answers
Answer:
True
Step-by-step explanation:
6^3, or 6x6x6, is equal to 216.
---
hope it helps
Answer:
true
Step-by-step explanation:
Find the Unit Price for each bottle of conditioner. Which bottle of hair conditioner is the best buy?
8 oz for $1.49
12 oz for $2.29
15 oz for $2.75
20 oz for $3.89
Answers
Answer:
D.
Step-by-step explanation:
We know that to find unit price, we divide the unit in the numerator by the quantity in the denominator.
For the first option, we must put $1.49 as the numerator and 8 as the denominator. It will then look like this:
\(\frac{1.49 / 8 }{8 / 8\\}\) Then we must divide 1.49 by 8. This will get us $0.18625.For our second option, we must put $2.29 as the numerator, and 12 as the denominator. It will look like this:
\(\frac{2.29 / 12 }{12 / 12\\}\) Then we must divide 2.29 by 12. This will get us $0.19083 (rounded)For our third option, we must put $2.75 as the numerator, and 15 as the denominator. It will look like this:
\(\frac{2.75 / 15 }{15 / 15}\)Then we must divide 2.75 by 15. This will get us $\(0.18333\) (rounded)For our final option, we must put $3.89 as the numerator, and 20 as the denominator. It will look like this:
\(\frac{3.89 / 20 }{3.89 / 20}\)Then we must divide 3.89 by 20. This will get us $0.1945 (rounded)Therefore, the last option is the best buy because $0.18625 > $0.18333.
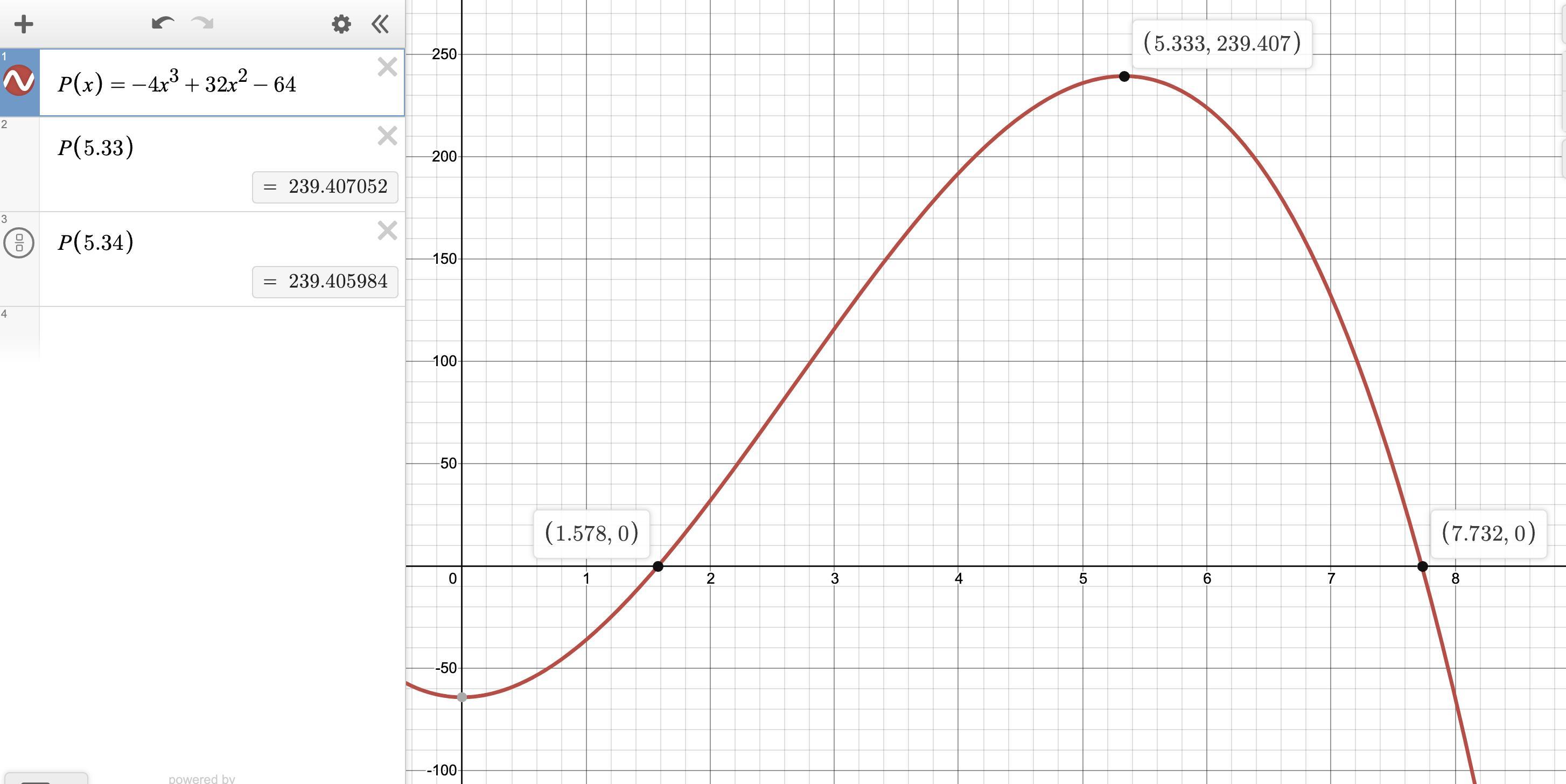
A company that sells toys models their profit with the function
P(x) = −4x3 + 32x2 − 64. Their profit P, in thousands of dollars,
is a function of the number of toys sold x measured in hundreds.
What do the key features of the graph reveal about the profits?
What is the maximum profit the company can make?
Answers
9514 1404 393
Answer:
a) profit has a typical curve: negative at low volume, and again at very high volume.
b) $239,407
Step-by-step explanation:
a) The graph is negative below x=1.58, so the break-even point is 158 toys sold. The profit declines steeply above 533 toys sold, to again go negative for 774 toys sold. This sort of curve seems fairly typical.
__
b) The profit is a maximum of $239,407 when 533 toys are sold.
solve for x
2(x - 3 1/2)=10 3/4
Answers
exact form
x=71/8
Decimal Form:
x=8.875
Mixed Number Form:
x= 8 7/8
Answer:
Step-by-step explanation:
8 7/8
what are the portfolio weights for a portfolio that has 135 shares of stock a that sell for $84 per share and 110 shares of stock b that sell for $82 per share? (do not round intermediate calculations and round your answers to 2 decimal places, e.g., 32.1616.) portfolio weight stock a % stock b %
Answers
The portfolio weights for stock A and stock B are approximately 55.69% and 44.31%, respectively.
To calculate the portfolio weights for stock A and stock B, we need to determine the total value of the portfolio and the proportion of each stock's value within that total.
The total value of the portfolio can be calculated as follows:
Total value = (Number of shares of stock A × Price per share of stock A) + (Number of shares of stock B × Price per share of stock B)
Total value = (135 × $84) + (110 × $82)
Total value = $11,340 + $9,020
Total value = $20,360
Now, we can calculate the portfolio weights for each stock:
Weight of stock A = (Value of stock A ÷ Total value) × 100%
Weight of stock A = (($84 × 135) ÷ $20,360) × 100%
Weight of stock A = $11,340 ÷ $20,360
Weight of stock A ≈ 0.5569 or 55.69%
Weight of stock B = (Value of stock B ÷ Total value) × 100%
Weight of stock B = (($82 × 110) ÷ $20,360) × 100%
Weight of stock B = $9,020 ÷ $20,360
Weight of stock B ≈ 0.4431 or 44.31%
Therefore, the portfolio weights for stock A and stock B are approximately 55.69% and 44.31%, respectively.
To learn more about portfolio weights from the given link
https://brainly.com/question/30944975
#SPJ4
Describe a law you would pass to protect the bees from pesticides. How would this law be enforced?
Answers
Step-by-step explanation:
-Apply pesticides in the evening. Many pesticides are extremely toxic to honey Bees and other beneficial insects.
-Choose the appropriate formulation.
-Use less toxic, rapidly degradable pesticides.
-Alter application method.
-Establish apiaries in safe locations.
I hope I helped.
A significance test about a proportion is conducted using a significance level of 0.05. The sample statistic is 0.12. The p-value is 0.03? a) If H0 were true, for what probability of a Type I error was the test designed?
b) What conclusion (reject or fail to reject) would you make for this test?
c) If this test resulted in a decision error, what type of error was it?
Answers
Answer: 28282
Step-by-step explanation:
I think
State the conditions required for a random variable x to follow a poisson process.
Answers
The conditions required for a random variable X to follow a Poisson process. The probability of success is the sme for aany two intervals of equal length. The probability of two or more successes in any sufficiently small subinterval is 0.
Is the time required to upload a file to the Internet discrete or continuous?Is the length of time it takes to download a file from the Internet a random variable, a continuous random variable, or not at all? A continuous random variable, that is.Is the a discrete random variable a continuous random variable or not a random variable?A variable whose value is determined by counting is referred to as a discrete variable. A continuous variable is one whose value may be determined through measurement. A random variable is a variable whose value is the resultant number of an unpredictable event. There are a countable number of potential values for the discrete random variable X.How do you determine whether the random variable is discrete or continuous?A discrete variable is one that is random. if the number of possible values is either countable or finite. Continuous refers to a variable that is random. if the range of possible values includes all conceivable numbers.
Learn more about continuous function here:
https://brainly.com/question/18102431
#SPJ4
A 9th order, linear, homogeneous, constant coefficient differential equation has a characteristic equation which factors as follows.
(r^2+6r+10)^2r^2(r-1)^3=0
Write the nine fundamental solutions to the differential equation. Use t as the independent variable.
Answers
The nine fundamental solutions to the differential equation are:
\(e^{(-3+i)t}, e^{(-3-i)t}, e^t, te^t,\) 1, t, t²/2!, t³/3!, \(t^4\)/4!, \(e^{(-5+i)t}, ~and ~e^{(-5-i)t}\)
We have,
The characteristic equation of the given differential equation is:
\((r^2 + 6r + 10)^2 \times r^2 (r - 1)^3 = 0\)
We can find the fundamental solutions by looking at the roots of the characteristic equation.
The roots can be categorized as follows:
Roots of multiplicity 2 = -3 + i and -3 - i
Roots of multiplicity 2 = 1
Root of multiplicity 1 = 0
Root of multiplicity 2 = -5 + i and -5 - i
For each of these roots, we need to find the corresponding fundamental solution.
For the roots (-3 + i) and (-3 - i), the corresponding fundamental solutions are:
\(e^{(-3+i)t}~ and~ e^{(-3-i)t}\)
For root 1, the corresponding fundamental solutions are:
\(e^t~and~te^t\)
For the root 0, the corresponding fundamental solutions are:
1, t, t²/2!, t³/3!, ..., \(t^8\)/8!
For the roots (-5 + i) and (-5 - i), the corresponding fundamental solutions are:
\(e^{(-5+i)t} ~and~e^{(-5-i)t}\)
Therefore,
The nine fundamental solutions to the differential equation are:
\(e^{(-3+i)t}, e^{(-3-i)t}, e^t, te^t,\) 1, t, t²/2!, t³/3!, \(t^4\)/4!, \(e^{(-5+i)t}, ~and ~e^{(-5-i)t}\)
Learn more about fundamental solution here:
https://brainly.com/question/30465018
#SPJ11
A 4-column table with 4 rows titled Population Data. Column 1 has entries 4, 5, 9, 15. Column 2 has entries 8, 2, 20, 1. Column 3 has entries 6, 9, 10, 8. Column 4 has entries 10, 8, 1, 2.
If Serena selects 4 samples from the table, which row will give her largest mean?
Which row will give her the smallest mean?
The actual population mean will be between
Answers
Answer: Row 3
Row 2
6 and 10
Step-by-step explanation: C B A
Suppose that a certain population obeys the logistic equation dy/dt = ry[1 - (y/K)]. a. If y0 = K/3, find the time at which the initial population has doubled. Find the value of corresponding to r = 0.025 per year. b. If y0/K = , find the time T at which y(T)/K = . where 0 < < 1. Observe that T as 0 or as 1. Find the value of T for r = 0.025 per year, = 0.1, and = 0.9.
Answers
Suppose that a certain population obeys the logistic equation dy/dx= ry[1-(y/k)]
a) So if y0= K/3, then
dy/dx= ry[1-(y/k)]
The above statement is equation 1.
Equation 2 is in the form of
dy/dx + P(t)y = yⁿQ(t)
which is a Bernoulli's differential equation with n=2. So 1- 2= -1
To solve it we put
Then dz/dx= -y⁻²(dy/dx)
This above statement is equation 3.
P(t)= -r, Q(t)= -(r/K)
and integrating factor is given by
IF= e ∫(1-n)P(t)dt= e ∫(-1)(-r)dt= ert
Then the solution is given by
z(IF)= ∫(1-n)Q(t)(IF)dt+C
If given y0= K/3, then
3/K= 1/K+C
Thus the solution to this part is
y⁻1ert= ert/K+2/K= 1/K(2+ert)
To find the time at which the initial population doubled that is 2K/3
Thus
2K/3= Kert/(2+ert)
For r=0.025, then r= 55.452
Learn more about Bernoulli's differential equation here brainly.com/question/21852102
#SPJ4
Suppose $x-3$ and $y+3$ are multiples of $7$. What is the smallest positive integer, $n,$ for which $x^2+xy+y^2+n$ is a multiple of $7$? Enter your answer. I need Immediate help or you wont get the points.
Answers
In the language of modular arithmetic, we're given
\(x-3\equiv0\pmod7\implies x\equiv3\pmod7\)
\(y+3\equiv0\pmod7\implies y\equiv-3\equiv4\pmod7\)
Then x = 7a + 3 and y = 7b + 4 for integers a and b.
Substitute these into the quadratic expression and simplify:
\(x^2+xy+y^2+n\equiv0\pmod7\)
\((7a+3)^2+(7a+3)(7b+4)+(7b+4)^2+n\equiv0\pmod7\)
\(49a^2+42a+9+49ab+28a+21b+12+49b^2+56b+16+n \equiv 0\pmod7\)
\(37+n\equiv 0\pmod7\)
\(n\equiv-2\equiv5\pmod7\)
which means the smallest positive integer n we are looking for is 5.
which of the following lines are parallel.
Lines a and b
lines a and c
Lines b and c

Answers
The lines which are parallel are none.
What is the slope?The slope is the ratio of the vertical changes to the horizontal changes between two points of the line.
m = ( y₂ - y₁ ) / ( x₂ - x₁ )
where (x₁, y₁) and (x₂, y₂) are the two points that you are trying to find the slope between.
Given;
Coordinates of three lines
a;(1,5) and (-2,-4)
b;(3,2) and (1,-4)
c;(6,1) and (-4,2)
Now, slopes of the lines
a= -4-5/-2-1
=10/3
b=-4-2/1-3
=-3
c=2-1/-4-6
=1/-10
Therefore, by slopes of the line none of them are parallel.
Learn more about slope here:
https://brainly.com/question/2503591
#SPJ1
R-1.3 Algorithm A uses 10n log n operations, while algorithm B uses n2 operations. Determine the value n0 such that A is better than B for n ≥ n0.
R-1.4 Repeat the previous problem assuming B uses n √n operations.
I only need R-1.4!!
Answers
For n ≥ 459, Algorithm A is better than Algorithm B when B uses n√n operations.
To determine the value of n₀ for which Algorithm A is better than Algorithm B when B uses n√n operations, we need to find the point at which the number of operations for Algorithm A is less than the number of operations for Algorithm B.
Algorithm A: 10n log n operations
Algorithm B: n√n operations
Let's set up the inequality and solve for n₀:
10n log n < n√n
Dividing both sides by n gives:
10 log n < √n
Squaring both sides to eliminate the square root gives:
100 (log n)² < n
To solve this inequality, we can use trial and error or graph the functions to find the intersection point. After calculating, we find that n₀ is approximately 459. Therefore, For n ≥ 459, Algorithm A is better than Algorithm B when B uses n√n operations.
Learn more about Algorithm here:
https://brainly.com/question/24953880
#SPJ11
R-1.3: For \($n \geq 14$\), Algorithm A is better than Algorithm B when B uses \($n^2$\) operations.
R-1.4: Algorithm A is always better than Algorithm B when B uses \($n\sqrt{n}$\) operations.
R-1.3:
Algorithm A: \($10n \log n$\) operations
Algorithm B: \($n^2$\) operations
We want to determine the value of \($n_0$\) such that Algorithm A is better than Algorithm B for \($n \geq n_0$\).
We need to compare the growth rates:
\($10n \log n < n^2$\)
\($10 \log n < n$\)
\($\log n < \frac{n}{10}$\)
To solve this inequality, we can plot the graphs of \($y = \log n$\) and \($y = \frac{n}{10}$\) and find the point of intersection.
By observing the graphs, we can see that the two functions intersect at \($n \approx 14$\). Therefore, for \($n \geq 14$\), Algorithm A is better than Algorithm B.
R-1.4:
Algorithm A: \($10n \log n$\) operations
Algorithm B: \($n\sqrt{n}$\) operations
We want to determine the value of \($n_0$\) such that Algorithm A is better than Algorithm B for \($n \geq n_0$\).
We need to compare the growth rates:
\($10n \log n < n\sqrt{n}$\)
\($10 \log n < \sqrt{n}$\)
\($(10 \log n)^2 < n$\)
\($100 \log^2 n < n$\)
To solve this inequality, we can use numerical methods or make an approximation. By observing the inequality, we can see that the left-hand side \($(100 \log^2 n)$\) grows much slower than the right-hand side \($(n)$\) for large values of \($n$\).
Therefore, we can approximate that:
\($100 \log^2 n < n$\)
For large values of \($n$\), the left-hand side is negligible compared to the right-hand side. Hence, for \($n \geq 1$\), Algorithm A is better than Algorithm B when B uses \($n\sqrt{n}$\) operations.
So, for R-1.4, the value of \($n_0$\) is 1, meaning Algorithm A is always better than Algorithm B when B uses \($n\sqrt{n}$\) operations.
To know more about Algorithm, refer here:
https://brainly.com/question/28724722
#SPJ4

Is it correct? Please tell me I’m not sure lol I’ll give brainliest

Answers
and omg i love your handwriting!
which statement is true about this graph
A: The slope is -6
B: the relationship is proportional
(I already know that:
The equation of the line is y= - 3x
and that the slope is negative.)

Answers
B: the relationship is proportional
suppose that g is a graph with n vertices such that every vertex has degree n/2. if the graph is represented using the adjacency list representation, then what is the worst-case complexity to determine whether two particular vertices are adjacent?
Answers
The worst-case time complexity to determine whether two particular vertices are adjacent in this graph is O(n).
In the worst-case scenario, we need to examine all the edges incident to both vertices to determine whether they are adjacent or not. Since each vertex has degree n/2, there are n/2 edges incident to each vertex. Therefore, in the worst case, we need to examine n/2 + n/2 = n edges.
In the adjacency list representation, we can find the list of adjacent vertices for a given vertex in O(n) time by scanning the adjacency list for that vertex. Therefore, to examine all the edges incident to both vertices, we need to scan the adjacency lists of both vertices, which takes O(n) time for each vertex.
Thus, the worst-case time complexity to determine whether two particular vertices are adjacent in this graph is O(n).
Visit to know more about Vertices:-
brainly.com/question/1217219
#SPJ11
Maria went shopping at Macy's. She bought a pair of slacks that were on sale for 15%. The original price was $40.00 dollars. She bought a shirt that was on sale for 14% off the original price of $30.00. She had to pay a tax of 6.79%. What was the total amount of her sale?
Answers
Answer:
3.27
Step-by-step explanation:
please help me with this!!!

Answers
Answer:
yea
Step-by-step explanation: