Harry buys a TV priced at £1200 plus 20% VAT.
He pays £300 deposit and the balance in ten equal monthly payments.
Calculate each monthly payment.
Answers
Answer:
£ 114
Step-by-step explanation:
From the question given above, the following data were obtained:
Price of TV = £ 1200
VAT = 20%
Amount paid = £ 300
Amount paid monthly =.?
Next, we shall determine the VAT. This can be obtained as follow:
VAT = 20% of price of TV
VAT = 20/100 × 1200
VAT = £ 240
Next, we shall determine the total cost of the TV. This can be obtained as follow:
Price of TV = £ 1200
VAT = £ 240
Total cost of TV =?
Total cost = Price + VAT
Total cost = 1200 + 240
Total cost = £ 1440
Next, we shall determine the balance amount he needs to pay. This can be obtained as follow:
Total cost = £ 1440
Amount paid = £ 300
Balance amount =?
Balance = Total cost – Amount paid
Balance = 1440 – 300
Balance = £ 1140
Finally, we shall determine the amount Harry will pay month.
Balance Amount = £ 1140
Number of months = 10
Amount paid monthly =.?
Amount paid monthly = Balance / number of month
Amount paid monthly = 1140 / 10
Amount paid monthly = £ 114
Therefore, Harry will pay £ 114 monthly.
Related Questions
3. What is the power output of an engine that does 60,000 J of work in 10 s?
Answers
the answer to the problem is 6 KILA watts
Important Formula:
\(p=\dfrac{w}{t}\)
Where p is power(measured in watts), w is work(measured in joules), and t is time(measured in seconds).
\(w=60,000J\)
\(t=10s\)
\(p=?\)
____________
\(p=\dfrac{w}{t}\)
____________
\(p=\dfrac{60,000}{10}\)
____________
\(\fbox{p = 6,000 watts}\)
x³ by a³ + a³by x³=p x³by a³- a³by ³=q eliminate x
Answers
Answer:
Step-by-step explanation:
\(\frac{x^3}{a^3} +\frac{a^3}{x^3} =p\\\frac{x^3}{a^3} -\frac{a^3}{x^3} =q\\adding\\2\frac{x^3}{a^3} =p+q\\\frac{x^3}{a^3} =\frac{p+q}{2} \\substitute~in~first\\\frac{p+q}{2} +\frac{2}{p+q} =p\\\frac{(p+q)^2+4}{2(p+q)} =p\\(p+q)^2+4=2p(p+q)\\p^2+q^2+2pq+4-2p^2-2pq=0\\q^2-p^2+4=0\\q^2=p^2-4\)
How do I figure out x and y

Answers
Answer:
x = 7, y = 45
Step-by-step explanation:
\(7x+13=6x+20\)
\(x=20-13\\x=7\)
Angle
\(7(7)+13=49+13=62^{0}\)
supplementary angle
180 - 62 = 118°
\(3y-17=118\)
\(y=\frac{118+17}{3} =135/3=45\)
Hope this helps
Dylan has a pitcher with 1.65 L of orange juice. He pours out 0.2 L
of the juice. Then he adds some sparkling water to the pitcher to
make orangeade. He ends up with 1.9 L of orangeade. Solve the
equation 1.65 -0.2 + x = 1.9 to find the amount of sparkling
water, x, Dylan adds to the pitcher. Show your work.
Answers
Answer:
Step-by-step explanation:
fork knife
The Graduate Management Admission Test (GMAT) is used by many graduate schools of business as one of their admission criteria. Using your own reasoning and concepts, criticize each of the following conclusions.
Statements
a. "Last year, 7,573 computer science majors took the GMAT, compared with only 588 philosophy majors. Philosophy majors must not be interested in business because so few take the GMAT."
b. "Last year, 29,688 engineering majors took the GMAT, compared with only 3,589 English majors. Clearly, more students major in engineering than in English."
c. "Last year, physics majors averaged 100 points higher on the GMAT than marketing majors. If marketing students majored in physics, they would score better on the GMAT."
d. "On average, physics majors score higher on the GMAT than accounting majors. Therefore, physics majors would make the best managers."
Answers
Answer:
Ideez
Step-by-step explanation:
Find the length of DC.

Answers
Answer:
sqart(89) in
Step-by-step explanation:
As triangle ABC is a right triangle, so sqrt(5^2 + 8^2) = sqrt(89) approximately 9.43 in.
Fraser scores 43% in a spelling test. What percentage did he get wrong?
Answers
Answer:
57% incorrect
Step-by-step explanation:
100- 43= 57. Assuming that the test is out of 100%, he got 57% of the test incorrect
Find the slope of the tangent line to the curve defined by 4x2+5xy+y4=370
at the point (−9,−1)
Answers
Answer:
The slope of the tangent line to the curve at the given point is -11/7.
Step-by-step explanation:
Differentiation is an algebraic process that finds the gradient (slope) of a curve. At a point, the gradient of a curve is the same as the gradient of the tangent line to the curve at that point.
Given function:
\(4x^2+5xy+y^4=370\)
To differentiate an equation that contains a mixture of x and y terms, use implicit differentiation.
Begin by placing d/dx in front of each term of the equation:
\(\dfrac{\text{d}}{\text{d}x}4x^2+\dfrac{\text{d}}{\text{d}x}5xy+\dfrac{\text{d}}{\text{d}x}y^4=\dfrac{\text{d}}{\text{d}x}370\)
Differentiate the terms in x only (and constant terms):
\(\implies 8x+\dfrac{\text{d}}{\text{d}x}5xy+\dfrac{\text{d}}{\text{d}x}y^4=0\)
Use the chain rule to differentiate terms in y only. In practice, this means differentiate with respect to y, and place dy/dx at the end:
\(\implies 8x+\dfrac{\text{d}}{\text{d}x}5xy+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
Use the product rule to differentiate terms in both x and y.
\(\boxed{\dfrac{\text{d}}{\text{d}x}u(x)v(y)=u(x)\dfrac{\text{d}}{\text{d}x}v(y)+v(y)\dfrac{\text{d}}{\text{d}x}u(x)}\)
\(\implies 8x+\left(5x\dfrac{\text{d}}{\text{d}x}y+y\dfrac{\text{d}}{\text{d}x}5x\right)+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
\(\implies 8x+5x\dfrac{\text{d}y}{\text{d}x}+5y+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
Rearrange the resulting equation in x, y and dy/dx to make dy/dx the subject:
\(\implies 5x\dfrac{\text{d}y}{\text{d}x}+4y^3\dfrac{\text{d}y}{\text{d}x}=-8x-5y\)
\(\implies \dfrac{\text{d}y}{\text{d}x}(5x+4y^3)=-8x-5y\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{-8x-5y}{5x+4y^3}\)
To find the slope of the tangent line at the point (-9, -1), substitute x = -9 and y = -1 into the differentiated equation:
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{-8(-9)-5(-1)}{5(-9)+4(-1)^3}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{72+5}{-45-4}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=-\dfrac{77}{49}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=-\dfrac{11}{7}\)
Therefore, slope of the tangent line to the curve at the given point is -11/7.
A zip wire runs between two posts, 25m apart. The zip wire is at an angle of 10∘ to the horizontal. Calculate the length of the zip wire.
Answers
The length of the zip wire is approximately 25.42 meters.
To calculate the length of the zip wire, we can use trigonometry and the given information about the angle and the distance between the two posts.
Given:
Distance between the two posts: 25m
Angle of the zip wire to the horizontal: 10°
We can use the trigonometric function cosine (cos) to find the length of the zip wire. Cosine relates the adjacent side to the hypotenuse of a right triangle.
In this case, the adjacent side is the distance between the two posts (25m) and the hypotenuse is the length of the zip wire that we want to calculate.
Using the cosine function:
cos(angle) = adjacent/hypotenuse
cos(10°) = 25m/hypotenuse
To find the hypotenuse (length of the zip wire), we can rearrange the equation:
hypotenuse = 25m / cos(10°)
Using a calculator or trigonometric tables, we can find the value of cos(10°) to be approximately 0.9848.
Therefore, the length of the zip wire is:
hypotenuse = 25m / 0.9848 ≈ 25.42m
For more such questions on length
https://brainly.com/question/2217700
#SPJ8
Find the value of x and y in simplified radical form.

Answers
x and y have the values 7 and 7√2, respectively.
The sides of a right triangle with 45-degree acute angles have a unique ratio of 1:1:2.
We can use this information to determine the values of x and y because the base is specified as being 7.
Let's give the perpendicular side the value of x, and the hypotenuse the value of y.
The perpendicular side (x) and the base (7) have the same length because the acute angles are both 45 degrees.
Consequently, x = 7.
We can determine that x:y:2x using the ratio of 1:1:2.
When we enter the value of x, we may calculate y:
7:y:√2(7)
Simplifying even more
7:y:7√2
Given that the hypotenuse (y) equals 72, we can write:
y = 7√2
Thus, x and y have the values 7 and 7√2, respectively.
Learn more about right triangle click;
https://brainly.com/question/30966657
#SPJ1
A fighter jet F and a helicopter H leave the airport A at the same time. The jet flies 25 km on a bearing of 040° and the helicopter flies 30 km on a bearing of 320°. How far apart are the aircraft? (Use a scale of 1 cm to represent 5 km.)
Answers
Answer:
FH = 35.64
Step-by-step explanation:
(∠A = 360 so the other angle is 40)
By law of cosines,
FH² = AH² + FA² - 2(AH)(FA) * cos(A)
= 30² + 25² - 2(30)(25) * cos(80)
= 900 + 625 - 1500 * 0.17
= 1525 - 255
FH² = 1270
FH = √1270
FH = 35.64

Many delivery trucks feature a "How Am I Driving?” sticker on the rear bumper, along with a phone number. This sticker allows drivers to report erratic driving by the truck driver or offer a compliment if they like. A dispatcher at the trucking station accepts calls and records information from those who call the phone number. The dispatcher reports that in the past month, 218 calls were received. Of those calls, 178 reported negative driving behaviors by the truck drivers. How might this data-collection method produce bias in obtaining an estimate of all drivers who are satisfied with the company’s truck drivers?
This sample may lead to nonresponse bias because many drivers may not call the phone number.
This sample may lead to undercoverage bias because some drivers will be more likely to be included in the sample.
The sample may lead to response bias because some who call the phone number may not provide a truthful opinion.
This sample may lead to voluntary response bias because drivers can choose to call the phone number and register an opinion.
Answers
The way in which this data-collection method produce bias in obtaining an estimate of all drivers who are satisfied with the company’s truck drivers is that: D. This sample may lead to voluntary response bias because drivers can choose to call the phone number and register an opinion.
What is sampling bias?A sampling bias can be defined as a type of bias in which members of an intended population are selected in such a way that some members have a higher or lower sampling probability (chances) than the other members.
This ultimately implies that, a sampling bias would occur when members of an intended population are selected incorrectly and as such resulting in a sample that is not representative of the entire population.
Generally speaking, a voluntary response sample is a data-collection technique (method) that is always biased because it only include individuals who choose to volunteer, unlike a simple random sample.
Read more on sampling bias here: https://brainly.com/question/15062060
#SPJ1
Jada earns $7 an hour mowing her neighbors’ lawns
Answers
What is (123
) ÷ (18
)?
Answers
Answer:
6.8333333333 or 41/6
Step-by-step explanation:
Jeffrey needs $200 to buy a new iPod. Right now, he has $75. What percent of the $200 does he have?
PLEASE HELPPP
Answers
Answer:
40%
Step-by-step explanation:
Answer:
If you need help on further questions like this, divide what he has to what he needs or his goal
in order to get 37.5% you have to divide 75/ 200
You will get 0.357 and that is 37.5% this is ABOUT 40% but I reccomend putting 37.5% to be safe.
The diagram shows a shape made from a solid cube and a solid cylinder.
The cube has sides of length 8.7 cm.
The cylinder has a radius of 2.7 cm and a height of 4.9 cm.
Calculate the total surface area of the solid shape.
Give your answer correct to 3 significant figures.
Answers
The total surface area of the solid shape made from the cube and cylinder is approximately 583.31 cm².
How to calculate the areaThe side length of the cube is 8.7 cm, so the surface area of one face is A = 8.7²
= 75.69 cm²
Since there are six faces, the total surface area of the cube is 6 * 75.69 = 454.14 cm²
Since there are two circular bases, the total surface area of the bases is 2 * 22.91 = 45.82 cm².
In this case, the radius of the cylinder is 2.7 cm and the height is 4.9 cm, so the curved surface area is A_curved = 2 * π * 2.7 * 4.9 ≈ 83.35 cm².
Total surface area = surface area of the cube + surface area of the cylinder
Total surface area = 454.14 cm² + 45.82 cm² + 83.35 cm²
Total surface area ≈ 583.31 cm²
Learn more about area on
https://brainly.com/question/25292087
#SPJ1
Help&EXPLAIN
Don’t use for points or I’ll take it back and report

Answers
Answer:
x= 120°
Step-by-step explanation:
By first method-
exterior angle= sum of two opposite interior angle
x= 60°+60°
x = 120°
By second method-
sum of interior angles of triangle is= 180°
Let one interior angle be y
then
60°+60° +y = 180°
120°+y= 180°
y= 180°-120°
y= 60°
Now
x+y = 180°[ linear pair]
x+ 60°=180°[y=60°]
x= 180°-60°
x=120°
Hope it helps please give brainliest
Determine the value of x.
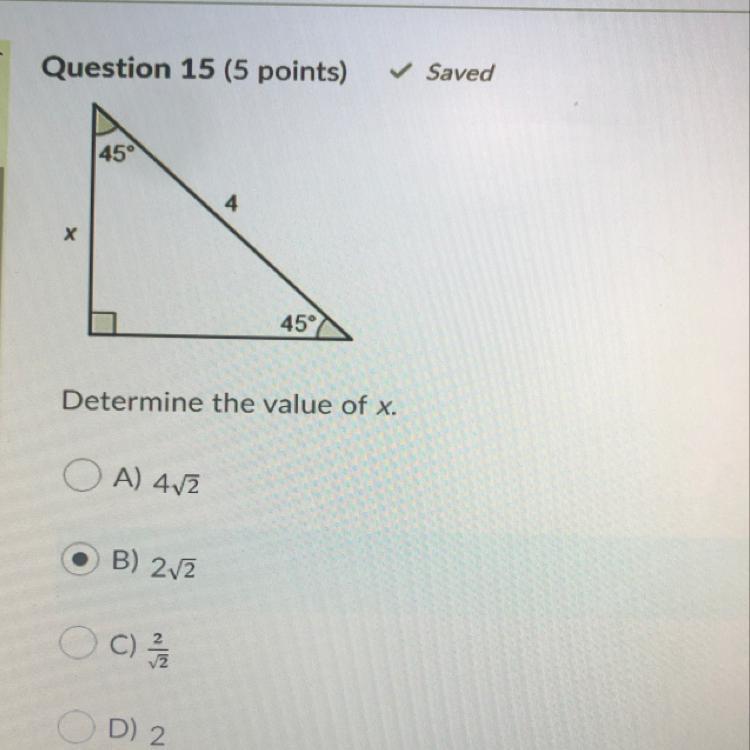
Answers
Answer:
2\(\sqrt{2}\)
Step-by-step explanation:
A 45-90-45 triangle will have two equivalent side lengths and the hypotenuse. The hypotenuse is 4 and one of the side lengths is x. Since one of the side lengths is x, the other side length is x as well. Using the Pythagorean theorem, you can create this equation:
x^2 + x^2 = 4^2
or
2x^2 = 16
Now do the algebra:
2x^2 = 16
x^2 = 8
x = \sqrt{8\\}
which can be simplified as 2\(\sqrt{2}\)
A scientist has two solutions, which she has labeled Solution A and Solution B. Each contains salt. She knows that Solution A is 65% salt and Solution B is 90% salt. She wants to obtain 150 ounces of a mixture that is 80% salt. How many ounces of each solution should she use?
Answers
The amount of solution A and B required are 60 and 90 ounces respectively.
Creating simultaneous equations for the problem:
Mass of solution A = a
Mass of solution B = b
a + b = 150 _____(1)
0.65a + 0.90b = 150×0.80
0.65a + 0.90b = 120 __(2)
From (1)
a = 150-b ____(3)
substitute (3) into (2)
0.65(150-b) + 0.90b = 120
97.5 - 0.65b + 0.90b = 120
0.25b = 120-97.5
0.25b = 22.5
b = 22.5/0.25
b = 90
a = 150 - b
a = 150 - 90
a = 60
Therefore , 60 ounces of solution A and 90 ounces of solution B is required.
Learn more on simultaneous equations:https://brainly.com/question/148035
#SPJ1
write an exponential model given two points:
(10, 140) and (11,220)
Answers
Why is the answer 2 in the subtractive equation 1+1?
Answers
Answer:
That's not a subtractive equation, the symbol that you used indicates that it is an addition equation. if the question was 1-1 then the answer wouldn't be 2 but since the question is 1+1 the answer is 2
Step-by-step explanation:
find the direction angle of the given vector. give your answer in degrees in the interval . round to the nearest hundredth (2 decimal places). give just the number without the degree symbol.
Answers
The Direction Angle Of The Given Vector is θ = 59.086
Given :
The Direction Angle Of The Given Vector. V <-3,5) Give Your Answer In Degrees In The Interval [0°, 360°). round to the nearest hundredth (2 decimal places). give just the number without the degree symbol.
what is Direction angle of vector ?
The direction angle of a vector v is the angle from the positive x -axis to v .using the arc tangent of the ratio of the vertical component of the vector and the horizontal component of the vector.
tan θ = b / a
= 5 / -3
= -5 / 3
= 1.67
θ = tan^-1 ( 1.67 )
θ = 59.086
Learn more about the angle here:
https://brainly.com/question/28451077
#SPJ4
How would you know the answer (important)

Answers
Answer:
okay so I can't see the last option on ur sheet but when u graph this equation the point that lies on the curve is (2,-3) so that is the vertex but if I move up this curved line it passes through the Y axis at (0,-1), the Last answer that I can't see it wouldn't happen to be (-1,6) would it
simplify 9/14divided7/10
Answers
Answer:
45/49
Step-by-step explanation:
The first step to dividing fractions is to find the reciprocal (reverse the numerator and denominator) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. Finally, simplify the fractions if needed.
9/14 * 10/7 = 90/98
divide the numerator and the denominator by 2.
90 * 2 = 45
98 * 2 = 49
45/49
Define associative property
Answers
Answer:
the way in which factors are grouped in a multiplication problem does not change the product.
Step-by-step explanation:
Evaluate the expression
if x = 2, y = 3, and z = 4.
2x²-y + 2(z-1)
Answers
Answer:
11
Step-by-step explanation:
Substituting the values of x, y, and z into the expression, we get:
2x² - y + 2(z-1) = 2(2)² - 3 + 2(4-1)
= 2(4) - 3 + 2(3)
= 8 - 3 + 6
= 11
Therefore, if x = 2, y = 3, and z = 4, then the value of the expression 2x² - y + 2(z-1) is 11.
Answer:
11
Step-by-step explanation:
if x = 2, y = 3, and z = 4.
2x²-y + 2(z-1)
Substituting the given values of x, y, and z, we get:
2x² - y + 2(z-1) = 2(2)² - 3 + 2(4-1)
= 2(4) - 3 + 2(3)
= 8 - 3 + 6
= 11
Therefore, the value of the expression when x = 2, y = 3, and z = 4 is 11.
BODMAS (Brackets, Order, Division, Multiplication, Addition, Subtraction) is used to determine the sequence of operations in a mathematical expression. It is used to avoid confusion and ensure that everyone obtains the same answer from a mathematical expression. The rule states that the operations inside the brackets must be done first, followed by orders, then division and multiplication (from left to right), and finally addition and subtraction (from left to right).
There are 300 seeds in a packet of flower seeds.
Each seed will grow into a white flower or a yellow flower or a red flower.
The probability of a seed growing into a white flower is 0.62
45 of the seeds are expected to grow into yellow flowers.
One of the seeds is chosen at random from the packet.
What is the probability that this seed will grow into a red flower?
(3 marks)
Answers
Answer:
.23
Step-by-step explanatio
45 of the seeds will be yellow. So the probability of a yellow flower is
45/300 = .15
Total probability = probability of white + probability of yellow + probability of red
or
1 = P(W) + P(Y) + P(R)
we know P(W) = .62. So let x = probability of a red flower
1 = .62 + .15 + x
1 = .77 + x
x = .23
) In a geometric progression, the sum of the first two terms is equal to 16. The sum to infinity is equal to 25. Find the possible values of the first term.
Answers
There are no possible real values for the first term 'a' that satisfy both equations.
Let's denote the first term of the geometric progression as 'a' and the common ratio as 'r'.
The sum of the first two terms can be expressed as:
a + ar = 16
To find the sum to infinity, we can use the formula:
Sum to infinity = a / (1 - r)
Given that the sum to infinity is 25, we have:
25 = a / (1 - r)
We now have two equations:
a + ar = 16
a / (1 - r) = 25
We can solve these equations simultaneously to find the possible values of 'a'.
From the first equation, we can factor out 'a' to get:
a(1 + r) = 16
Dividing both sides of the second equation by 25, we have:
a / (1 - r) = 1
We can rearrange this equation to get:
a = 1 - r
Substituting this expression for 'a' in the first equation, we get:
(1 - r)(1 + r) = 16
Expanding the equation, we have:
1 - r^2 = 16
Rearranging the terms, we get:
r^2 = -15
Since we are dealing with a geometric progression, the common ratio 'r' must be a real number. However, we observe that r^2 = -15 has no real solutions. Therefore, there are no possible real values for the first term 'a' that satisfy both equations.
for such more question on real value
https://brainly.com/question/27371101
#SPJ8
Three-fourths of the yard is covered with grass and one-fourth is used as a garden. The sprinkler could only water 1/5 of the yard, so the rest died. Use the model to find out how much of the grass died.
Answers
3/5 or 60% of the grass died because the sprinkler could only water 1/5 of the yard.
Let's start by breaking down the information given:
- Three-fourths of the yard is covered with grass.
- One-fourth of the yard is used as a garden.
- The sprinkler could only water 1/5 of the yard.
To find out how much of the grass died, we need to determine the portion of the grass that was not watered by the sprinkler.
Let's assume the total area of the yard is represented by the value 1. Therefore, we can calculate the area of the grass as 3/4 of the total yard, which is (3/4) * 1 = 3/4.
The sprinkler can only water 1/5 of the yard, so the portion of the grass that was watered is (1/5) * (3/4) = 3/20.
To find the portion of the grass that died, we subtract the watered portion from the total grass area:
Portion of grass that died = (3/4) - (3/20) = 15/20 - 3/20 = 12/20.
Simplifying, we get:
Portion of grass that died = 3/5.
Therefore, 3/5 or 60% of the grass died because the sprinkler could only water 1/5 of the yard.
for more such question on grass visit
https://brainly.com/question/6204338
#SPJ8
If a figure is a rectangle, it is a parallelogram.
P: a figure is a rectangle
Q: a figure is a parallelogram
which represents the inverse of this statement is the inverse true or false 
Answers
The inverse statement is false.
The inverse of the statement "If a figure is a rectangle, it is a parallelogram" would be:If a figure is not a rectangle, then it is not a parallelogram.To determine if the inverse is true or false, we need to evaluate its validity. In this case, the inverse statement is false. Just because a figure is not a rectangle does not mean it cannot be a parallelogram. There are other types of parallelograms, such as squares and rhombuses, that are not rectangles. Therefore, the inverse statement is false.For such more questions on inverse
https://brainly.com/question/3831584
#SPJ8