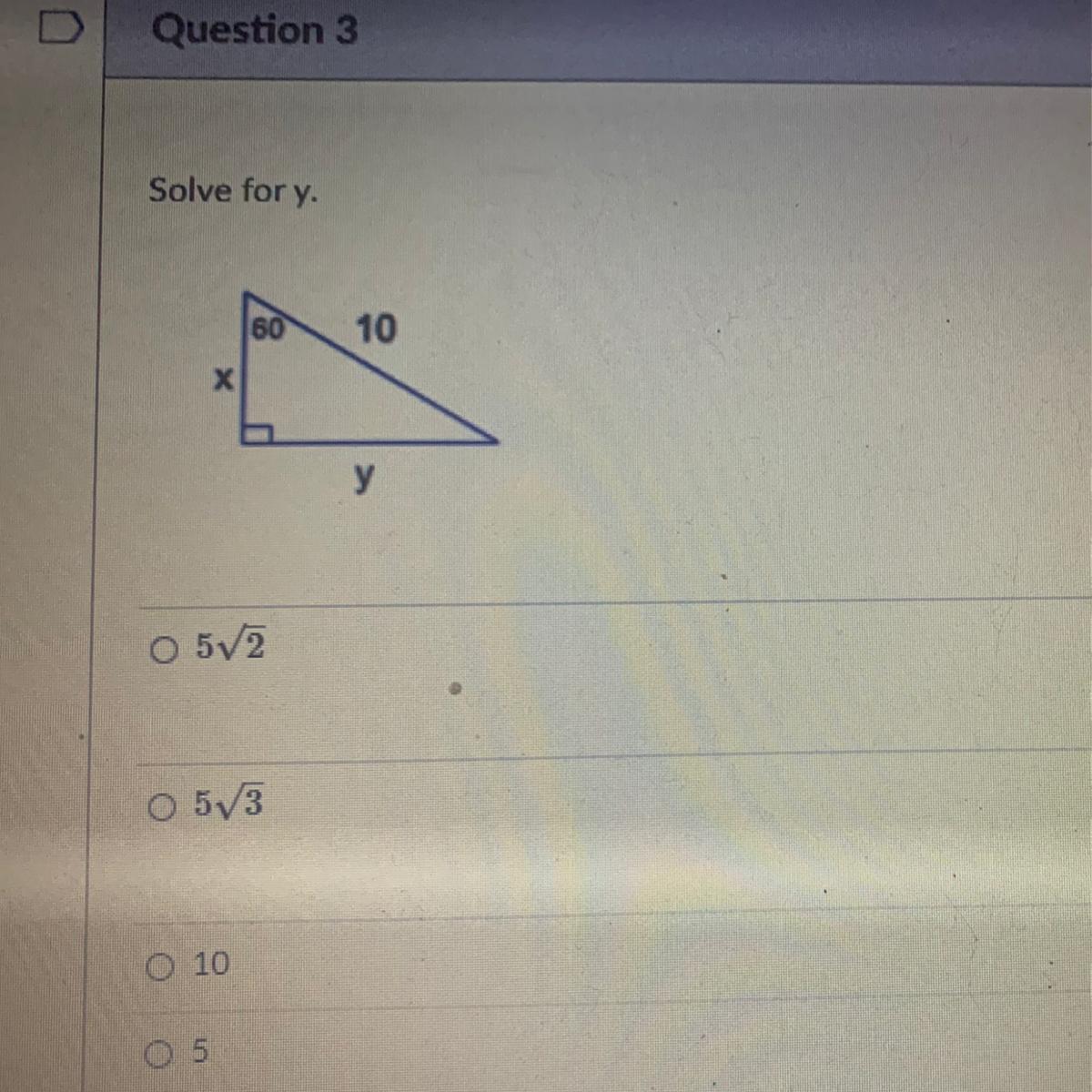
Answers
Answer:
10
Step-by-step explanation:
Hope It Helps
BRAINLIEST PLEASE
Related Questions
A study conducted at a certain college shows the 30% of the school graduates find a job in their chosen field within a year after graduation. Find the probability that among 14 randomly selected graduates at least one finds a job in his or her chosen field within a year of graduating. Assume the sample is taken with replacement.
Answers
find the median of the following 3,6,7,4,5,9,8,9,7
please please please please help help help help help help help me me me me me me me me me me
ratios equivalent to 3:12
Answers
Answer:
3:12 equivalent ratios are 6:24, g:36
Step-by-step explanation:
Given: select two ratios that are equivalent to 3:12
Solution:
\(\frac{3\times2}{12\times2}=\frac{6}{24}=6:24\)
\(\frac{3\times3}{12\times3}=\frac{g}{36}=g:36\)
i hope this helps you :D
Answer:
Step-by-step explanation:
Ratios equivalent to 3:12 are:
1:4
6:24
9:36
12:48
15:60
Hope this helps!
Write an equation in slope-intercept form (-5,-7);y=-2x+4
Answers
Answer:
Step-by-step explanation:
First, let us substitute x and y values: -7 = -2(-5) + 4
Next, let us simplify using the substitution property of equality: 14 = -7 (SEE BELOW MORE INFO).
Now, this does not make sense yet because 14 cannot possibly equal -7. Therefore, we must add a b value, therefore leading us to the equation:
14 + b = -7
by simplifying, we can conclude that b = -21
Finally, we can plug in the b-value into our original equation:
y = -2x + 4 - 21
After simplifying, we get y = -2x - 17. When this is graphed, we can see that -2x - 17 intersects (-5, -7).
help,for,points and brainliest math easy math hi a b c d e f g h i j k l m n o p q r s t u v w s y and z

Answers
D. 21
E. 30
PLEASE.
Tell whether the angles are complementary or supplementary. Then find the value of x.

Answers
Dan made 8 out of 10 free throws. What is the experimental probability that he will not make his next free throw? What is the theoretical probability of not making a free throw?
Answers
Answer:
8/10--> 2/10 20 % scnahce of not makin git
Step-by-step explanation:
Solve the equation. 4x - x = 4 - 25
Answers
Answer:
x=-7
Step-by-step explanation:
Simplify both sides of the equation then divide by 3
A rectangular prism has a length of 12 in., a width of 5 in., and a height of 414 in. The prism is filled with cubes that have edge lengths of 14 in. How many cubes are needed to fill the rectangular prism? Enter your answer in the box.
Answers
Answer:
The answer is 16320
I took the test
Answer:
16320
Step-by-step explanation:
Same i took it
F(x)=(x+2)^2 (x-3) graph the function
Answers
The value of the equation f ( x ) is
f ( x ) = x³ + x² - 8x - 12
What is an Equation?
Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Now , the value of A is
f ( x ) = ( x + 2 )²( x -3 ) be equation (1)
Now , on simplifying the equation , we get
f ( x ) = ( x + 2 )²( x -3 )
f ( x ) = ( x² + 4x + 4 ) ( x - 3 )
Now , multiplying each term with ( x - 3 ) , we get
f ( x ) = ( x - 3 ) x² + ( x - 3 ) 4x + ( x - 3 ) 4
f ( x ) = x³ - 3x² + 4x² - 12x + 4x - 12
On simplifying the equation ,we get
f ( x ) = x³ + x² - 8x - 12
Now , the value of the equation f ( x ) = x³ + x² - 8x - 12
On graphing the equation , we get
The graph of the equation f ( x ) = x³ + x² - 8x - 12 is shown below
To learn more about equations click :
https://brainly.com/question/10413253
#SPJ1

Determine the mean, median, mode and midrange for the following data:
13 15 18 18 21
Your answers should be exact numerical values.
The mean of the data is
The median of the data is
The mode of the data is
The midrange of the data is
Answers
The Mean is 17, Median is 18, Mode is 18 and, Midrange is 17.
The Mean is defined as the ratio of sum of numbers present in the data to the total numbers present in the data. Median is defined as the ratio of sum of middle numbers present in the data. Mode is defined as the most recurring number present in the data. Midrange is the ratio of the largest and smallest number in the data to 2.
Let's see how to calculate Mean, Median, Mode and Midrange.
Mean = 13 + 15 + 18 + 18 + 21 / 5
Mean = 85 / 5
Mean = 17
Median = 18 (as it is the middle term of the data)
Mode = 18 (as it is most recurring number)
Midrange = 21 + 13 / 2
Midrange = 34 / 2
Midrange = 17
Therefore, The Mean is 17, Median is 18, Mode is 18 and, Midrange is 17.
To study more about Mean, Median Mode:
https://brainly.com/question/14532771
https://brainly.com/question/542771
Need help ASAP
the value of each variable. If your answer is not
teger, express it in simplest radical form.
The length of a is
The length of b is
(Simplify your answer.)

Answers
Answer:
me too (help)
Step-by-step explanation:
What is the intersection of the lines given by 2y=-x+3 and -y=5x+1? Enter the answer as an ordered pair.
Answers
Answer:
(-5/9, 16/9)
Step-by-step explanation:
2y = -x + 3
-y = 5x + 1
To find the intersection, you need to substitute the y-value from the second equation into the first equation. Rearrange the second equation so that it is equal to y.
-y = 5x + 1
-1(-y) = -1(5x + 1)
y = -5x - 1
Substitute this equation into the y-value of the first equation.
2y = -x + 3
2(-5x - 1) = -x + 3
-10x - 2 = -x + 3
(-10x - 2) + 2 = (-x + 3) + 2
-10x = -x + 5
(-10x) + x = (-x + 5) + x
-9x = 5
(-9x)/(-9) = (5)/(-9)
x = -5/9
Plug this x value into one of the equations and solve for y.
2y = -x + 3
2y = -(-5/9) + 3
2y = 5/9 + 3
2y = 32/9
(2y)/2 = (32/9)/2
y = 32/18 = 16/9
The ordered pair is (-5/9, 16/9).
Please help fast! Determine which set of side measurements could be used to form a right triangle. 4, 8, 11 or 6, 8, 13 or square root of 3, square root of 5, 8 or square root of 3, square root of 13, 4.
Answers
The following sets of side dimensions could be combined to create a right triangle 6, 8, 13 is √3, √13, 4.
What is a right-angle triangle?In the triangle, there are three angles: two acute angles and one 90-degree angle. The hypotenuse, perpendicular, and base are the terms used to describe the sides of a right-angled triangle.
The next choice shows the triangle's side length:
The point is,
The hypotenuse square of a right-angled triangle is equal to the sum of its squares on its other two sides, according to Pythagoras' Theorem.
Using Pythagoras' Theorem.
Use the formula:
a² + b² = c²
For 4, 8, 11
4, 8, 11
4² + 8² = 16 + 64 = 80
11² = 121
80 is not equal to 121 it cann ot form a right triangle
For 6, 8, 13
6² + 8² = 36 + 64 = 100
13² = 169
100 is equal to 169 - 69 can form a right triangle
For √3, √5, 8
(√3)² + (√5)² = 3 + 5 = 8
8² = 64
8 is equal to 64 cannot form a right triangle
For √3, √13, 4
(√3)² + (√13)² = 3 + 13 = 16
4² = 16
16 is equal to 16 can form a right triangle
In order to create a right triangle, one may utilise the following set of side measurements √3, √13 and 4 form a triangle.
To know more about right triangle, visit:
https://brainly.com/question/28908116
#SPJ1
What is the meaning of "\( \varphi (x,y)\) be \( y\wedge \phi (x)\) "?
![What is the meaning of "[tex] \varphi (x,y)[/tex] be [tex] y\wedge \phi (x)[/tex] "?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/qBCO5ypO9m13MpdV66LMvZB6FUp8SIQM.png)
Answers
The reasoning presented lacks explicit explanations and logical connections between the steps, making it difficult to fully understand the intended proof strategy.
The given proof aims to show that the Separation Axioms can be derived from the Replacement Schema using a particular construction involving a formula p(x, y). Let's analyze the proof step by step:
Define the formula p(x, y) as x = yo(x).
This formula states that for each x, y pair, x is equal to the unique object y such that y is obtained by applying the operation o to x.
Define the set F as {(x, x) (x)}.
This set F contains pairs (x, x) where x is the unique object obtained by applying the operation (x) to x.
Claim: F(X) = {y (x = X)p(x, y)} = {y: (x = X)x = y^o(x)} = {x: (3x € X)o(x)} = {x X: (x)}.
This claim asserts that F(X) is equivalent to {y (x = X)p(x, y)}, which is further equivalent to {y: (x = X)x = y^o(x)}, and so on.
The proof states that since (x, y) satisfies the functional formula VaVyVz(p(x, y)^(x, z) y = z), it follows that (x, y) is a functional formula.This step emphasizes that the formula p(x, y) satisfies certain properties that make it a functional formula, which is relevant for the subsequent deductions.
Finally, the proof concludes that the Separation Axioms follow from the Replacement Schema, based on the previous steps.
For more such questions on explicit
https://brainly.com/question/30394385
#SPJ8
What is the point-slope form of a line with slope 3/2 that contains the point
(-1, 2)?
A.y+2=(x + 1)
B. y-2-(x-1)
C. y+2=(x-1)
D. y-2-(x+1)
Answers
Answer:
\(\boldsymbol{\rm{y-2=\dfrac{3}{2}(x+1)}}\), or DStep-by-step explanation:
Hello
If a line's equation has the form \(\boldsymbol{\rm{y-y1=m(x-x1)}}\), then it's considered to be in point-slope form.
In that formula,
\(\boldsymbol{\rm{y1}}\) is the y co-ordinate (2nd co-ordinate) of the point (here it's given as 2)\(\boldsymbol{\rm{m}}\) is the slope, here it's 3/2\(\boldsymbol{\rm {x1}}\) is the x co-ordinate (the first co-ordinate) of the point.Now you know why this equation is called point-slope form!
Now that we're familiar with the equation, let's plug in the information that's given to us...
\(\boldsymbol{\rm{y-2=\displaystyle\frac{3}{2}(x-(-1)}}\) | simplify
\(\boldsymbol{\rm{y-2=\displaystyle\frac{3}{2}(x+1)}}\)
\(\pmb{\tt{done~!!}}\)
\(\orange\hspace{300pt}\above3\)
y - 2=(x+1) , or D because its rlly simple u just need to ask someone else for help.
Solve the right triangle. Round decimal answers to the nearest tenth.
PLS PLSS HELPPPP 25 POINTSSS

Answers
Answer:
Step-by-step explanation:
\(14^2 = b^2+6^2\\b^2 = 14^2-6^2\\b = \sqrt{14^2-6^2} \\ = \sqrt{160}\\ = 12.6491106407\)
Rounding off to nearest tenth:
b ≈ 12.6
tanθ = 6/12.6
\(tan^{-1} (6/12.6)\\ = 25.46334506\\\)
Hence angle A ≈ 25.5
Angle B = 180-25.5-90
Angle B = 64.53665494
Hence, Angle B ≈ 64.5
Feel free to mark as brainliest
(g) Every student of class IV donated as much money as their number to make a fund for landslide, If there are 68 students in class IV how much money did they collect?
Answers
Answer:$2346
Step-by-step explanation: Assuming that the students' numbers start at 1, we have 1+2+3+4.....+65+66+67+68 as the total amount of money raised. We can see that 1+68 = 69 and 2+67 also equals 69. So, we can use this method to figure out how many 69s are in the sum. Since 68 divided by 2 is 34, there are 34 69s in the sum. 34x69 = 2346.
leyes logicas de la matematica
Answers
Step-by-step explanation:
Leyes conmutativas. ...
- Leyes asociativas. ...
- Leyes distributivas. ...
- Leyes de idempotencia. ...
- Leyes de Morgan.
URRRRRGGGGEEENNNNTTTTT!!!!!!

Answers
Step-by-step explanation:
Well you have to find two points on the line like points (0,2) and (2,-2)
Then you do y2-y1/x2-x1
You should be able to know what answer it is now!
Hope this helps <3
Diane plans to arrive 30 minutes early on Friday. What time does she plan to arrive?
*
7:00 A.M.
8:30 A.M.
8:00 A.M.
6:30 A.M.
7:30 A.M.

Answers
Diane plans to arrive at 7:30 A.M.
What is time ?
Time is a notion that is used to quantify the length and progression of occurrences. It is a key aspect of how things work and can be expressed in terms of hours, minutes, seconds, and other time intervals. Time helps us schedule, coordinate, and comprehend the sequence of events in our daily lives. It also enables us to arrange and synchronize activities.
If we take the assumed intended arrival time of 8:00 A.M. and deduct Diane's anticipated arrival time of 30 minutes, we get the intended arrival time.
Therefore, Diane plans to arrive at 7:30 A.M.
Learn more about time here :brainly.com/question/24662469
#SPJ1
|x-2| > square root (x)
Answers
Answer:
x = 0
Step-by-step explanation:
I. When x cant be negative value and
II. Find possible positive value
If x = 0
|0-2| > \(\sqrt{0}\)
|-2| > 0
2 > 0 true
If x = 1
|1 - 2| > \(\sqrt{1}\)
| -1 | > 1
1 > 1 false
More question or something to discuss, leave comment below
Answer:
Step-by-step explanation:
x ≥ 0 (because the square root)
\(|x-2| > \sqrt{x}\\\\1)\ if \ x-2 >0 \ (\ or\ x > 2):\\|x-2|=x-2\\\\x-2 > \sqrt(x) \Longrightarrow\ (x-2)^2 > x\\\Longrightarrow\ x^2-4x+4 > x\\\Longrightarrow\ x^2-5x+4 > 0\\\Longrightarrow\ (x-1)(x-4) > 0\\\Longrightarrow\ x<1\ or\ x>4 \Longrightarrow\ x >4 \ (since\ x>2)\\\\\)
\(2)\ if\ x-2 <0 \ (\ or\ x < 2):\\|x-2|=-(x-2)=-x+2\\\\-x+2 > \sqrt(x) \Longrightarrow\ (-x+2)^2 > x\\\Longrightarrow\ x^2-4x+4 > x\\\Longrightarrow\ x^2-5x+4 > 0\\\Longrightarrow\ (x-1)(x-4) > 0\\\Longrightarrow\ x<1\ or\ x>4 \Longrightarrow\ x\geq 0\ and \ x\leq 1 \\\)
Sol= [0, 1] ∪ ]4,+∞) ***** corrected

Scenario: Does the age at which babies learn to crawl depend on the time of the year that the babies were born? Data were collected from parents who brought their babies into the University of Denver’s Infant Study Center to participate in one of a number of experiments between 1988 and 1991. Parents reported the birth month and the age in which their child first began to crawl. The resulting data were grouped by month of birth: January, May, and September.
Answers
The age for when babies learn to crawl is different for Januar,May, and September.. so I guess yes?
Write an equation in slope-intercept form for the line that passes through the given point and is perpendicular to the graph of the given equation: (-3,-2) y=x+2
Answers
Given :
A point ( -3 , -2 ).
An equation of a line, y = x + 2.
To Find :
An equation in slope-intercept form for the line that passes through the given point and is perpendicular to the graph of the given equation.
Solution :
Let, equation of new line is :
y = mx + c ....1)
Here, m and c are slope and intercept respectively.
We know, product of slope of two line is -1 :
m( 1 ) = -1
m = -1
It is also given that point ( -3,-2 ) passes through this point.
Putting value of this point and slope in equation 1), we get :
\(-2 = (-1)\times ( -3 ) + c\\\\c = -2 -3\\\\c = -5\)
Therefore, the equation of line is : y = -x -5 .
Find the area of the triangle. round your answer to the nearest tenth

Answers
Answer:
use photo math
Step-by-step explanation:
cuz i said so
Answer is A 234.6 units
Explanation:
Area = base * side * sinγ ( Sin of angle)/2
A = 37 * 30·sin(25°)/2
A ≈ 234.55314 units
In a class of students, the following data
table summarizes how many students have a
cat or a dog. What is the probability that a
student chosen randomly from the class has
a cat?
Has a dog
Does not have a
dog
Has a cat
2
3
Does not have a
cat
12
10
Answers
The table can be summarized as follows:
| | Has a dog | Does not have a dog |
|----------|-----------|---------------------|
| Has a cat | 2 | 3 |
| Does not have a cat | 12 | 10 |
To find the probability that a student chosen randomly from the class has a cat, we need to find the total number of students who have a cat (regardless of whether or not they have a dog), and divide it by the total number of students in the class.
The number of students who have a cat is 2 (those who have a dog and a cat) + 3 (those who have a cat but do not have a dog) = 5.
The total number of students in the class is the sum of all four categories: 2 (has a cat and a dog) + 3 (has a cat, does not have a dog) + 12 (does not have a cat, has a dog) + 10 (does not have a cat, does not have a dog) = 27.
So, the probability that a student chosen randomly from the class has a cat is 5/27.
A consumer affairs investigator records the repair cost for 4 randomly selected washers. A sample mean of $52.63 and standard deviation of $22.01 are subsequently computed. Determine the 80% confidence interval for the mean repair cost for the washers. Assume the population is approximately normal. Step 2 of 2 : Construct the 80% confidence interval. Round your answer to two decimal places.
Answers
Answer:
The 80% confidence interval for the mean repair cost for the washers is between $34.60 and $70.66.
Step-by-step explanation:
We have the standard deviation for the sample, which means that the t-distribution is used to solve this question.
The first step to solve this problem is finding how many degrees of freedom, we have. This is the sample size subtracted by 1. So
df = 4 - 1 = 3
80% confidence interval
Now, we have to find a value of T, which is found looking at the t table, with 3 degrees of freedom(y-axis) and a confidence level of \(1 - \frac{1 - 0.8}{2} = 0.9\). So we have T = 1.638
The margin of error is:
\(M = T\frac{s}{\sqrt{n}} = 1.638\frac{22.01}{\sqrt{4}} = 18.03\)
In which s is the standard deviation of the sample and n is the size of the sample.
The lower end of the interval is the sample mean subtracted by M. So it is 52.63 - 18.03 = $34.60
The upper end of the interval is the sample mean added to M. So it is 52.63 + 18.03 = $70.66.
The 80% confidence interval for the mean repair cost for the washers is between $34.60 and $70.66.
what is 3,108 rounded to the nearest thousand
Answers
Answer:
3100
Step-by-step explanation:
Answer:
3,000
Step-by-step explanation:
If the question was about 3,500 it would be rounded to 4,000
If the question was about 2,499 it would be rounded to 2,000
If it is in between 3,449 and 2,500 then it would be rounded to 3,000 which 3,108 is
The given table values represents a liner equation. What is the slope?
A. 2
B. 3
C. 1
D. 4

Answers
Answer:
A. 2
Step-by-step explanation:
\( slope (m) = \frac{y_2 - y_1}{x_2 - x_1} \)
Use any two points given in the table of values. Let's use (1, 5), (3, 9)
Let,
\( (1, 5) = (x_1, y_1) \)
\( (3, 9) = (x_2, y_2) \)
Plug these values into the slope formula:
\( slope (m) = \frac{9 - 5}{3 - 1} \)
\( slope (m) = \frac{4}{2} \)
\( slope (m) = 2 \)
Consider the following function. f(x) = 3x − e x i. Plot the graph of the function f(x) in R and identify the interval that the first positive root lies. Write the command(s) that you use and the result(s).
Answers
The interval of the function f(x) = 3 · x - eˣ such that the function shall be positive is x ∈ (0.6191, 1.5121).
How to find the interval of a function that cannot be solved for x analytically
In this question we have an expression that combines polynomic and exponential expression, whose variable x cannot be cleared by analytical approaches, but by numerical and graphical methods. Herein we decide to find the interval by graphical methods, using a graphing tool:
First, write the function in explicit form (f(x) = 3 · x - eˣ). Second, find the two points such that the function goes through the x-axis (horizontal axis). Third, define the set of possible x-values by interval notation such that y > 0.
Then, the points of the function that are on the x-axis are (x₁, y₁) = (0.6191, 0) and (x₂, y₂) = (1.5121, 0). Then, the interval of the function f(x) = 3 · x - eˣ such that the function shall be positive is x ∈ (0.6191, 1.5121).
To learn more on functions: https://brainly.com/question/12431044
#SPJ1

4. Verify the following for a = 3 and b = 4.
a) (a + b)^2= a^2 + 2ab + b^2
b)(a + b)^2 = a^2 - 2ab + b^2
c) (a + b)(a - b) = a^2 - b^2
Answers
Answer:
(3+4)^2=9+24+16
7^2
=49