Given y = x² + 3x - 2, find y when x = -2
Answers
Answer:
y = -4
Step-by-step explanation:
y = x² + 3x -2
y = (-2)² + 3(-2) - 2
y = 4 - 6 - 2
y = -4
I hope this helps!
y = x2 + 3x-2
y = (-2)2+3(-2) -2
y=4-6-2
y=-4
you simply plug in -2 anywhere you see an x.
Related Questions
Let X have an exponential probability density function with B = 500.
a. Compute Pr[X > 500).
b. Compute the conditional probability Pr[X > 1000 | X > 500).
Answers
a. The probability that X is greater than 500 is approximately 0.368.
b. The conditional probability that X is greater than 1000 is approximately 0.368.
a. To compute Pr[X > 500), we use the cumulative distribution function (CDF) of the exponential distribution, which is:
F(x) = 1 - e^(-x/B)
Plugging in B = 500 and x = 500, we get:
Pr[X > 500) = 1 - F(500) = 1 - (1 - e^(-500/500)) = e^(-1) ≈ 0.368
Therefore, the probability that X is greater than 500 is approximately 0.368.
b. To compute Pr[X > 1000 | X > 500), we use the definition of conditional probability:
Pr[X > 1000 | X > 500) = Pr[(X > 1000) ∩ (X > 500)] / Pr[X > 500)
Since X is a continuous random variable, we can rewrite the probability of the intersection using the minimum of X:
Pr[(X > 1000) ∩ (X > 500)] = Pr[X > max(1000, 500)] = Pr[X > 1000]
Plugging in B = 500 into the CDF, we have:
Pr[X > 1000] = 1 - F(1000) = 1 - (1 - e^(-1000/500)) = e^(-2) ≈ 0.135
We already know from part a that Pr[X > 500) = e^(-1) ≈ 0.368.
Putting it all together, we have:
Pr[X > 1000 | X > 500) = Pr[X > 1000] / Pr[X > 500) = (e^(-2)) / (e^(-1)) = e^(-1) ≈ 0.368
This result shows that the conditional probability that X is greater than 1000, given that it is already greater than 500, is the same as the probability that X is greater than 500 on its own. In other words, knowledge of the fact that X is already greater than 500 does not change our prediction about whether it will be greater than 1000 or not.
To know more about conditional probability refer here:
https://brainly.com/question/30144287
#SPJ11
How many and what type of solutions does the function represented by the graph have?

Answers
Answer:
Only one solution (x = 0)
Step-by-step explanation:
From the graph attached,
Parabola in the graph touches the origin.
It doesn't intersect the x-axis.
Therefore, There will be only one root or solution of the given function,
x = 0
Simplify the expression. ( 5 x 2 − 3 x ) − ( 5 x 2 − 3 x + 1 )
Answers
Answer:
-1
Step-by-step explanation:
Following PEMDAS The answer equals to -1
*plssss make me brainlist*
Answer:
Let's simplify step-by-step.
5x2−3x−(5x2−3x+1)
Distribute the Negative Sign:
=5x2−3x+−1(5x2−3x+1)
=5x2+−3x+−1(5x2)+−1(−3x)+(−1)(1)
=5x2+−3x+−5x2+3x+−1
Combine Like Terms:
=5x2+−3x+−5x2+3x+−1
=(5x2+−5x2)+(−3x+3x)+(−1)
=−1
Step-by-step explanation:
Show your work
what units do scientist use to measure force
Answers
Answer: newtons
Step-by-step explanation:
Answer:
I believe it is Newtons :)
Step-by-step explanation:
Kevin spent 10 hours doing homework last week. This week he spent 15 hours doing homework. He says that he spent 150% more time doing homework this week. Is he correct? Show your work to justify your decision.
Answers
What is 4 2/5 divided by 1 1/10
Answers
Answer:
✓ 4 2/5 divided by 1 1/10= 4
Step-by-step explanation:
✓ Factor the numerator and denominator and cancel the common factors.
✓ Hopefully this helps you!
-Keira
When \(4\frac{2}{5}\) is divided by \(1 \frac{1}{10}\) we get the value 4.
Convert mixed numbers to improper fractions:
\(4\frac{2}{5}\) = (4 × 5 + 2) / 5 = 22/5
\(1 \frac{1}{10}\) = (1 × 10 + 1) / 10 = 11/10
Divide the two fractions:
(22/5) ÷ (11/10)
To divide fractions, we multiply the first fraction by the reciprocal of the second fraction:
(22/5) × (10/11)
220/55
220/55 can be reduced by dividing both the numerator and denominator by their greatest common divisor, which is 5:
(220 ÷ 5) / (55 ÷ 5)
= 44/11
=4
To learn more on Division click:
https://brainly.com/question/21416852
#SPJ6
A shirt costs $34. Sales tax is 6%. What is the total amount including tax
Answers
Answer:
the answer is $36.04
Step-by-step explanation:
34 dived into 100= 0.34 times 6 equals 2.04 34+2.04=36.04
using the formula for calculating the number of communication channels, how many channels would two people require?
Answers
The number of communication channels, 1 channels would two people require.
To find number of communication channels, we use;
On the other hand, it might be a sign of the scope and intensity of the project communication management needed in huge projects and so-called megaprojects. This could, for example, entail allocating specific resources to project communication responsibilities in accordance to the number of available channels for communication. These factors may be especially important for teams working on sensitive projects and projects where information flow may be unclear or even fraudulent.
Number of potential communication channels = n x (n-1)/2
Given n = 2;
→ x = 2*(2 - 1)/2
= 2*1/2
= 1
The number of communication channels, 1 channels would two people require.
learn more about of factor here
https://brainly.com/question/24182713
#SPJ4
What is -2d-2 < 3d+8
Answers
Answer:
d > -2
Step-by-step explanation:
-2d-2 < 3d+8
3d+8 > -2d-2
3d + 2d > -2 -8
5d > -10
d > -2
Feel free to mark this as brainliest! :D
a sample of 942 homeowners are classified, in the two-way frequency table below, by the number of credit cards they have and the number of years they have owned their current homes. of the homeowners in the sample who have four or more credit cards, what proportion have owned their current homes for at least one year?
Answers
The probability that have owned their current homes for at least one year is 78/212
Given that,
In the two-way frequency table below, a sample of 942 homeowners is grouped according to how many credit cards they have and how long they have owned their current homes. of the sample's homeowners who possess four or more credit cards
To find : The probability that homeowners have lived in their current residences for at least a year
Required Probability
=( Number of homeowners having four or more credit cards and have
owned their current homes for at least one year /
Number of homeowners having four or more credit cards )
= 58+ 20/134 + 58 + 20
= 78/212
Hence, The probability that have owned their current homes for at least one year is 78/212
To learn more about probability click here:
brainly.com/question/11234923
#SPJ4
Given the following 25 sample observations:
5.3, 6.1, 6.7, 6.8, 6.9, 7.2, 7.6, 7.9, 8.1, 8.9, 9.0, 9.2, 9.4, 9.7, 10.1, 10.4, 10.6, 10.8, 11.3, 11.4, 12.0, 12.1, 12.3, 12.5, 13.2
And let Y1, Y2,...,Yn be the order statistics for this sample.
A) The interval (Y9, Y16) could serve as distribution-free estimate of the median, m, of the population. Find the confidence coefficient of this interval. (Not confidence interval)
B) The interval (Y3, Y10) could serve as the confidence interval forstudent submitted image, transcription available below. Determine this confidence interval and, using a binomial distribution chart, determine the confidence coefficient of this interval.
Answers
Given the following 25 sample observations:
5.3, 6.1, 6.7, 6.8, 6.9, 7.2, 7.6, 7.9, 8.1, 8.9, 9.0, 9.2, 9.4, 9.7, 10.1, 10.4, 10.6, 10.8, 11.3, 11.4, 12.0, 12.1, 12.3, 12.5, 13.2.
Let Y1, Y2,...,Yn be the order statistics for this sample.
A) The interval (Y9, Y16) could serve as a distribution-free estimate of the median, m, of the population.
Find the confidence coefficient of this interval.
The sample size is 25, thus the median is Y(13), where Y is the order statistics of the sample.
So the interval (Y(9), Y(16)) is a 75% confidence interval for the median, m, of the population.
The confidence coefficient of this interval is 0.75.
B) The interval (Y3, Y10) could serve as the confidence interval for a proportion.
Determine this confidence interval and, using a binomial distribution chart, determine the confidence coefficient of this interval.
To calculate the confidence interval for a proportion, we need to calculate the sample proportion, P and use that to calculate the interval limits.
The sample proportion, P = (number of success)/(sample size)
P = (number of success)/(25)
P = (7/25)
= 0.28
So the confidence interval for the proportion is given by:
p ± z √((p(1 - p)) / n)p ± z √((0.28(0.72)) / 25)p ± z √(0.02016 / 25)p ± z (0.1421)
The interval (Y3, Y10) contains 8 observations out of 25.
Thus, the sample proportion is:
P = 8/25
= 0.32
Using a binomial distribution chart, we find the z-value that corresponds to a cumulative area of 0.975 is 1.96.
Hence the 95% confidence interval for the proportion is:
p ± z √((p(1 - p)) / n)
0.32 ± 1.96 √((0.32(0.68)) / 25)0.32 ± 0.1421
The confidence interval is (0.1779, 0.4621) and the confidence coefficient is 0.95.
To know more about confidence visit:
https://brainly.com/question/32278466
#SPJ11
Let X = (X1 , X2 , X3)T be a multivariate normal random vector with mean vector mu = (1, 0, 2)T and variance-covariance matrix:
\sum = \begin{bmatrix} 1 & 0.5 & 0.5\\ 0.5 & 1 &0.5 \\ 0.5 & 0.5 & 1 \end{bmatrix}
a) Let W = X1 - X2 + X3. Find E[W].
b) Find Var(W).
c) Find P[W > 4].
d) Let U = 2X1 - X2 + X3. Find P[W > U].
Answers
a) We have:
W = X1 - X2 + X3
So, E[W] = E[X1] - E[X2] + E[X3] (by linearity of expectation)
Using the given mean vector, we get:
E[W] = 1 - 0 + 2 = 3.
(b) We have:
Var(W) = Var(X1) + Var(X2) + Var(X3) - 2Cov(X1,X2) - 2Cov(X1,X3) + 2Cov(X2,X3) (by the formula for variance of a sum of random variables)
Using the given variance-covariance matrix, we get:
Var(W) = 1 + 1 + 1 - 2(0.5) - 2(0.5) + 2(0.5) = 1.
(c) Since W is a linear combination of normal random variables, it follows that W is also normally distributed. Therefore, we can standardize W and use the standard normal distribution to find P[W > 4]:
P[W > 4] = P[(W - 3)/sqrt(Var(W))] = P[Z > (4-3)/1] = P[Z > 1],
where Z is a standard normal random variable. Using a standard normal table or calculator, we get:
P[Z > 1] = 0.1587 (approx).
(d) We need to find P[W > U], where U = 2X1 - X2 + X3. Since W and U are linear combinations of normal random variables, it follows that W - U is also normally distributed. Therefore, we can standardize W - U and use the standard normal distribution to find P[W > U]:
P[W > U] = P[(W - U)/sqrt(Var(W - U))] = P[Z > (0 - E[W-U])/sqrt(Var(W-U))],
where Z is a standard normal random variable. To find E[W-U] and Var(W-U), we compute:
E[W-U] = E[W] - E[U] = 3 - 2(1) + 0 = 1,
Var(W-U) = Var(W) + Var(U) - 2Cov(W,U) = 1 + 4 + 2(0.5) - 2(1.5) = 1.
Substituting these values, we get:
P[W > U] = P[Z > -1/sqrt(1)] = P[Z > -1],
where Z is a standard normal random variable. Using a standard normal table or calculator, we get:
P[Z > -1] = P[Z < 1] = 0.8413 (approx).
Click the below link, to learn more about mean vector:
https://brainly.com/question/30861900
#SPJ11
The area of parallelogram is 48 sq cm . If two adjacent sides are 8 cm and 6 cm. Find the length of diagonal.
Answers
The length of the diagonal of the parallelogram is 10 cm using the Pythagoras rule.
What is the Pythagoras ruleThe Pythagoras rule states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In the question, we observe that the diagonal of the parallelogram will form a right-angled triangle with the adjacent side of length 8cm and 6cm.
thus by Pythagoras rule;
the length of the diagonal = √(6² + 8²) cm
the length of the diagonal = √(36 + 64) cm
the length of the diagonal = √100 cm
the length of the diagonal = 10 cm
In conclusion, by proper application of Pythagoras rule we have derived the length of the diagonal of the parallelogram to be 10 cm.
Learn more about Pythagoras rule here:https://brainly.com/question/343682
#SPJ1
Find the measure of the missing angles. 34° b . c b = ° c = °
Answers
The sum of all the internal angle is \($180^{\circ}$\).
What is Internal angles?The internal angle formed by a closed polygon's sides inside of itself. A shape's interior can contain angles. The closed, side-and-vertex-containing shapes are known as polygons. All of the internal angles of a regular polygon are equal. For instance, the inner angles of a square are all exactly 90 degrees, or the right angle. Triangles always have three inner angles that add up to 180 degrees. Because the other two angles (180°+0°+0°) would not be present, a triangle cannot have an individual angle of 180°.The sum of all the internal angle is \($180^{\circ}$\).
\($$\angle A+\angle B+\angle C=180^{\circ}$$\)
1. 34 and 88
\(34+88+\angle C=180 \\\)
\(122+\angle C=180 \\\)
\(\angle C=180-122 \\\)
\(\angle C=58^{\circ}\)
2. 45 and 90
\(45+90+\angle C=180 \\\)
\(135+\angle C=180 \\\)
\(\angle C=180-135 \\\)
\(\angle C=45^{\circ}\)
3. 10 and 102
\(10+102+\angle C=180 \\\)
\(112+\angle C=180\)
\(\angle C=180-112 \\\)
\(\angle C=68^{\circ}\)
4. \($\boldsymbol{x}$\)and 50
\(x+50+\angle C=180 \\\)
\(\angle C=180-50-x \\\)
\(\angle C=(130-x)^{\circ}\)
The complete question is,
Find the measure of the third angle of a triangle given the measures of two angles.
1. 34 and 88
2. 45 and 90
3. 10 and 102
4. x and 50
To learn more about Internal angles refer to:
https://brainly.com/question/24966296
#SPJ1
Graph three points for y=x+2
Answers
Answer:
(0, 2)
(1, 3)
(2, 4)
What is the domain of the given function? {(3, –2), (6, 1), (–1, 4), (5, 9), (–4, 0)}
a {y | y = –4, –2, –1, 0, 1, 3, 4, 5, 6, 9}
b {y | y = –2, 0, 1, 4, 9}
c {x | x = –4, –2, –1, 0, 1, 3, 4, 5, 6, 9}
d {x | x = –4, –1, 3, 5, 6}
Answers
Hope this helps
You are making extra part kits for a game. The table below lists the number of each part needed per kit, as well as the number of each part that you have available.
Part Number in each kit Number available
People marker 6 287
6-sided die 3 143
Teleporter marker 7 341
You make as many kits as you can. With the parts remaining, you could make 1 more kit if you had:
A.1 more people marker and 1 more die.
B.1 more die and 1 more teleporter marker.
C.1 more teleporter marker and 1 more people marker.
D.2 more people markers.
E.2 more teleporter markers.
Answers
In order to make one more kit with the remaining parts, you would need 1 more people marker and 1 more die using mathematical operations
Let's analyze the number of parts available and the requirements for each kit. To make a kit, you need 6 people markers, 3 six-sided dice, and 7 teleporter markers. From the available parts, you have 287 people markers, 143 six-sided dice, and 341 teleporter markers.
We can determine the maximum number of kits you can make by dividing the available quantity of each part by the number required per kit. For the people markers, you have enough to make 287 / 6 = 47 kits. For the six-sided dice, you have enough to make 143 / 3 = 47 kits as well. Finally, for the teleporter markers, you have enough to make 341 / 7 = 48 kits.
After making the maximum number of kits, you will have some remaining parts. To determine if you can make one more kit, you need to identify the part(s) for which you have the least availability. In this case, the limiting factor is the people marker, as you have only 287 available. Therefore, to make one more kit, you would need 1 more people marker. Additionally, since you have 143 six-sided dice available, you also need 1 more die to match the requirement. Therefore, the answer is A. 1 more people marker and 1 more die.
Learn more about mathematical operations at https://brainly.com/question/28841790
#SPJ11
I NEED HELP WITH THIS!!!

Answers
Answer:
C)9,5,1,3
a1=9
a2=a(2-1)-4= a1-4= 9-4=5
a3=a(3-1)-4= a2-4= 5-4=1
Hope this will help :-)
Calculate the slope of the line that passes through the points (-4, -3) and (1,2)
Answers
Answer:
_______the answer is Y=X+1___________
determine the probability of each outcome when a loaded die is rolled, if a 3 is five times likely to appear as each of the other five numbers on the die
Answers
When the loaded die is rolled, the probability of getting a 1, 2, 4, 5, or 6 is 1/9 each, while the probability of getting a 3 is 5/9.
How to calculate the probabilities of outcomes when a loaded die is rolled?If a 3 is five times more likely to appear than each of the other five numbers on the die, we can assign the following probabilities to each outcome:
\(P(1) = P(2) = P(4) = P(5) = P(6) = x\) (some common probability)
\(P(3) = 5x\)
Since the sum of the probabilities for all possible outcomes must be equal to 1, we have:
\(P(1) + P(2) + P(3) + P(4) + P(5) + P(6) = x + x + 5x + x + x + x = 9x = 1\)
Solving for x, we get:
\(x = 1/9\)
Therefore, the probabilities for each outcome are:
\(P(1) = P(2) = P(4) = P(5) = P(6) = 1/9\\P(3) = 5/9\)
So when the loaded die is rolled, the probability of getting a 1, 2, 4, 5, or 6 is 1/9 each, while the probability of getting a 3 is 5/9.
Learn more about probability
brainly.com/question/30034780
#SPJ11
Solve the equation -8v – 5 = -21 for v.
Answers
Answer:
v=2
Step-by-step explanation:
add five to the other side and: -8v=(-21+5)
divide -16 by -8: v= -16/-8
v=2
not sure what the answer is

Answers
Given:
Base dimensions of a rectangular prism = 15 cm × x cm
The height of the prism = 8 cm
Volume of the prism = 600 cm.
To find:
The value of x.
Solution:
Base area of the prism is:
\(B=length\times width\)
\(B=15\times x\)
\(B=15x\)
Volume of the prism is:
\(V=Bh\)
Where, B is the base area and h is the height of the prism.
Putting \(V=600,B=15x,h=8\), we get
\(600=15x\times 8\)
\(600=(8)(15)x\)
\(\dfrac{600}{(8)(15)}=x\)
Therefore, the correct option is C.
A polygon is regular when all angles are equal and all sides are equal
True or False
Answers
Answer:
True
Step-by-step explanation:
True, because a polygon have all angles that are equal and all lengths are the same length.
If t and m are positive, t^2 + m^2 = 64 and (t+m)^2 = 98, what is tm?
(A) 162
(B) 130
(C) 81
(D) 34
(E) 17
Answers
Answer:
17
Step-by-step explanation:
t^2 + m^2 = 64
(t+m)^2 = 98
(t+m)^2 = t^2 +2tm+ m^2
==>
t^2 +2tm+ m^2 = 98
t^2+m^2+2tm=98
64+ 2tm=98
2tm = 98 -64
2tm=34
tm= 34/2
tm = 17
PLEASE HELP!!!!!!! Line M is represented by the following equation: x + y = −1 What is most likely the equation for line P so the set of equations has infinitely many solutions? (4 points) Question 5 options: 1) 2x + 2y = 2 2) 2x + 2y = 4 3) 2x + 2y = −2 4) x − y = 1
Answers
The equation for line P such that the system has an infinite number of solutions is given as follows:
3) 2x + 2y = -2.
How to obtain the equation?The first equation for the system of equations is given as follows:
x + y = -1.
A system of equations has an infinite number of solutions when the two equations are multiples.
Multiplying the equation by 2, we have that:
2x + 2y = -2.
Meaning that equation 3 is correct.
More can be learned about a system of equations at https://brainly.com/question/13729904
#SPJ1
i have a deck of cards, and i deal all of the cards to players, with each player getting cards. if is at least and is at least , then how many possible values of are there?
Answers
Answer:
4
Step-by-step explanation:
We want xy=54=2*3^3 such that x is at least 2 and y is at least 5. Thus, the possible combinations (x,y) are (2,27), (3,18), (6,9), and (9,6). There are 4 such combinations.
) find the original price of a pair of boots of the sale price is $120 after a 20% discount
Answers
Answer:
$150
Step-by-step explanation:
The sale price is $120. We're looking for 80% of the original price, given this sale price.
\(120 = .8p\)
\(p = 150\)
A rectangular solid and a cube are of equal volume. If the rectangular solid is 20 centimeters long, 5 centimeters wide, and 10 centimeters high, what is the length, in centimeters, of an edge of the cube?
Answers
Answer:
10 centimeters.
Step-by-step explanation:
First, we need to remember what's the formula to get the volume of a rectangular solid and a cube.
The volume of the first equals:
Volume = Length x Width x Height
While the volume of the cube is:
\(Volume = a^{3}\) where a is the edge.
We are given the measures of the rectangular solid so we can calculate its volume:
\(Volume= (20)(5)(10)=1000\) cubic cms.
Now, we know that both the volume of the rectangular solid and the cube are the same so we will use this information to calculate the edge of the cube.
\(1000=a^3 \\\sqrt[3]{1000} =\sqrt[3]{a^3} \\10=a\)
Thus the length of an edge of the cube is 10 centimeters
A farmer goes to the market to sell a box of eggs. A clumsy horse steps on the box of eggs and breaks a lot of them. The horse’s rider offers to pay for all of the eggs in the box and asks the farmer how many eggs there were. The farmer does not remember the exact number, but when she took them out of the box two at a time, there was 1 egg left. The same thing happened when she took them out three, four, five and six eggs at a time, but when she took them out 7 at a time, there were no eggs left
Answers
The smallest number of eggs that could have been in the box is 1134
The problem is to find the smallest number of eggs that could have been in the box, given the remainder when taking them out by different numbers. Here are the moves toward tackling it:
Allow n to be the quantity of eggs in the container. Then we have the accompanying arrangement of congruences:
n ≡ 1 (mod 2)
n ≡ 1 (mod 3)
n ≡ 1 (mod 4)
n ≡ 1 (mod 5)
n ≡ 1 (mod 6)
n ≡ 0 (mod 7)
For this problem, we have k = 6 k = 6, a i = {1,1,1,1,1,0} a_i = {1,1,1,1,1,0}, M i = {1260,840,630,504,420,720} M_i = {1260,840,630,504,420,720}, and y i = {−1,−2,−3,-4,-5,-6} y_i = {-1,-2,-3,-4,-5,-6}.
Plugging these values into the formula and simplifying modulo 5040, we get:
n = (−1260 + −1680 + −1890 + −2016 + −2100 + 0) mod 5040
n = (−8946) mod 5040
n = (−3906) mod 5040
n = 1134 mod 5040
Therefore, the smallest number of eggs that could have been in the box is 1134
to know more about congruences click here:
https://brainly.com/question/30818154
#SPJ4
Quick algebra 1 question for 10 points!
Only answer if you know the answer, quick shout-out to tariqareesha2 and MrBrainly, tysm for the help!
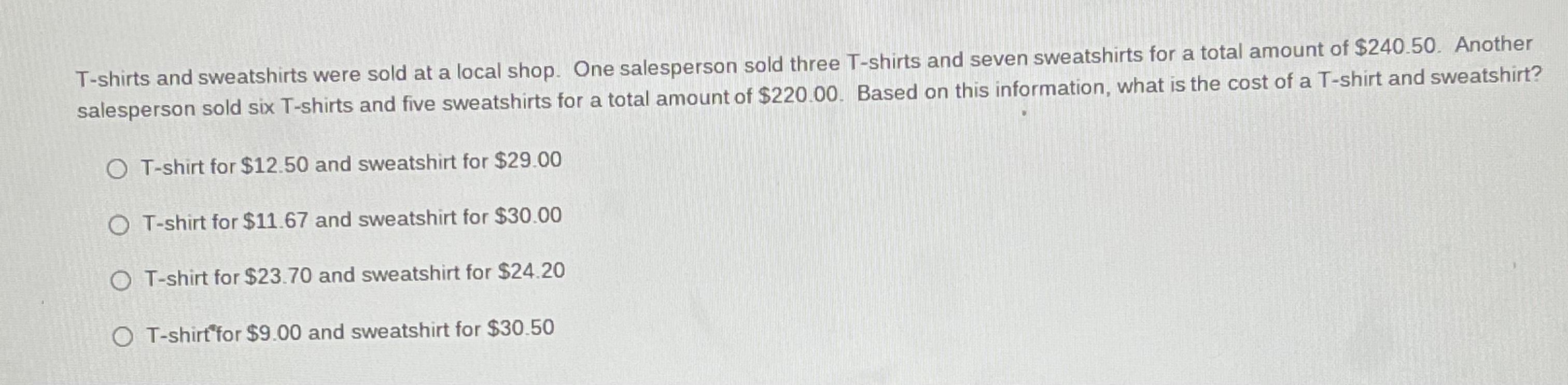
Answers
\(denote \: by \: s \: the \: cost \: of \: a \: sweatshirt \\ denote \: by \: t \: the \: cost \: of \: a \: t \: shirt\)
\(3t + 7s = 240.5 \\ 6t + 5s = 220\)
\( - 6t - 14s = - 481 \\ 6t + 5s = 220\)
\( - 9s = - 261 \\ s = \frac{ - 261}{ - 9} = 29 \: dollars\)
\(3t + 7(29) = 240.5 \\ \)
3t + 203 = 240.5
3t = 37.5
t = 12.5 dollars