Answers
Answer: The required scale factor\(=\dfrac43\)
Step-by-step explanation:
Formula : \(\text{Scale factor }=\dfrac{\text{Side in image}}{\text{Corresponding side in pre-image}}\)
Here, ED = 3 units in Δ DEF which corresponding to SR = 4 units in ΔRST
Now,
Scale factor for the given transformation = \(\dfrac{SR}{ED}\)
\(=\dfrac{4}{3}\)
hence, the required scale factor\(=\dfrac43\)
Related Questions
Help me quick please

Answers
Answer:
y ≤ 1/2x + 5
Step-by-step explanation:
-3x + 6y ≤ 30
add 3x on both sides:
6y ≤ 3x + 30
divide 6 on both sides:
y ≤ 3/6x + 30/6
This is simplified to:
y ≤ 1/2x + 5
the lifetimes of lightbulbs of a particular type are normally distributed with a mean of 392 hours and a standard deviation of 9 hours. find the 90th percentile.
Answers
The 90th percentile with a mean of 392 hours and a standard deviation of 9 hours is 403.538.
Given:
The lifetimes of light bulbs of a particular type are normally distributed with a mean of 392 hours and a standard deviation of 9 hours.
P(z<=?) = 0.90
z = 1.282
1.282 = x - mean / standard deviation
1.282 = x - 392 / 9
1.282 * 9 = x - 392
11.538 = x - 392
x = 392 + 11.538
x = 403.538.
Therefore the 90th percentile with a mean of 392 hours and a standard deviation of 9 hours is 403.538.
Learn more about the mean and standard deviation here:
https://brainly.com/question/28108712
#SPJ4
Select the correct answer from the drop-down menu. has vertices at , , and . The triangle is dilated by a factor of 3 with the center of dilation at vertex B, resulting in . What is ? Round to the nearest hundredth. units

Answers
Notice that, since B is the center of dilation, B'=B. Furthermore, is a dilation all the distances are enlarged by a factor equal to the dilation factor; thus,
\(\Rightarrow B^{\prime}C^{\prime}=3\cdot BC\)Calculate BC using the formula below,
\(\begin{gathered} P_1=(x_1,y_1),P_2=(x_2,y_2)_{} \\ \Rightarrow\text{distance}(P_1,P_2)=\sqrt[]{(x_1-x_2)^2+(y_1-y_2_{})^2} \end{gathered}\)Therefore,
\(\Rightarrow\text{distance}(BC)=\sqrt[]{(4-1)^2+(8-(-2))^2}=\sqrt[]{9+100}=\sqrt[]{109}\)Hence,
\(\begin{gathered} \Rightarrow B^{\prime}C^{\prime}=3\sqrt[]{109}=31.320919\ldots \\ \Rightarrow B^{\prime}C^{\prime}\approx31.32 \end{gathered}\)The answer is B'C'=31.32
Two opposite angles of a parallelogram are 3x+4 and 5x-2 find measure of all angles of parallelogram
Answers
Answer:
=The opposite angles of a parallelogram are equal
=(3x+4)
=(5x-2)
=-2x=-6
=x=6+2
=x=3=
1st angle=3x+4=13
3rd angle=5x-2=13
=sum of adjacent side of angle is 180°
=Let the adjacent (2nd angle ) be y=
y+13°=180°
=y=180°-13°
=y=167°=
2nd angle=4th angle
=2nd angle=167°
=4th angle=167°
Step-by-step explanation:
This might be confusing, but I hope it helps <3
who’s is combined thickness of these shims: 0.008, 0.125, 0.15, 0.185 and 0.005 cm?
Answers
0.338 is the answer
hope this helped
Based on the information, the combined thickness will be 0.3338.
From the information given, we are told to find the combined thickness of these shims: 0.008, 0.125, 0.15, 0.185 and 0.005 cm.
This simply means that we need to add the decimals. This will be:
= 0.008 + 0.125 + 0.15 + 0.185 + 0.005
= 0.3338 cm
Learn more about decimals on:
https://brainly.com/question/10975759
A useful graphical method of constructing the sample space for an experiment is:
a. a tree diagram
b. a pie chart
c. a histogram
d. an ogive
Answers
A useful graphical method of constructing the sample space for an experiment is a tree diagram that is option A.
A tree diagram is a useful graphical method of constructing the sample space for an experiment. It is a type of diagram used to represent the possible outcomes of an event. The diagram is structured in a way that each branch of the tree represents an event that can occur, and each level of the tree represents a stage in the experiment. By using a tree diagram, it is easier to visualize and understand all the possible outcomes of an experiment and the probabilities associated with each outcome. Therefore, option A is the correct answer.
To know more about graphical method,
https://brainly.com/question/29756293
#SPJ11
Helpppppppppppppppppppppp

Answers
Explanation:
There are 3 pretty points from the triagle on the graph.
They are (-4,3), (-2,-4), (3,-1)
Move those 3 order pairs x’s one unit to the LEFT!!
Making it (-5,3) (-3,-4) (2,-1)
Now move those 3 order pairs y’s 3 unit DOWN!!
Making it ( -5,0) (-3,-7) (2,-4)
In ADEF, the measure of ZF=90°, DE = 91 feet, and FD = 59 feet. Find the measure of D to the nearest degree.
Answers
ANSWER
m∠D = 50º
EXPLANATION
Triangle DEF is:
We want to know the measure of angle D, knowing the side lengths DE (the hypotenuse of the triangle) and FD (the adjacent side to angle D). We can use the cosine of D:
\(\begin{gathered} \cos \angle D=\frac{59}{91} \\ \angle D=\cos ^{-1}\frac{59}{91} \\ \angle D=49.58º\approx50º \end{gathered}\)
Help please:) and thx

Answers
Answer:
yes
Step-by-step explanation:
Write the converse of the following statement. If the converse is true, write "true." If it is not true, provide a counterexample If x < 0, then x5 < 0. Write the converse of the conditional statement. Choose the correct answer below. ? A. The converse "Ifx5 2.0, then x 2 0" is true. OB.The converse "If x 20 OC. O D. The converse "Ifx5 < 0, then x < 0" is true. 0 E. The converse "Ifx5 < 0, then x < 0" is false because x=0 is a counterexample. 0 F. The converse "Ifx5 20, then x 2 0" is false because x= 0 is a counterexample. then x5 20" is true. The converse "If x2 0, then x 0" is false because x= 0 is a counterexample
Answers
The converse of the following statement: If x < 0, then x5 < 0 is If x5 < 0, then x < 0. The answer is option D.
The converse "If x5 < 0, then x < 0" is true. Conditional statements are made up of two parts: a hypothesis and a conclusion. If the hypothesis is valid, the conclusion is also true, according to conditional statements. The inverse, converse, and contrapositive are three variations of a conditional statement that have different implications. The converse of a conditional statement is produced by exchanging the hypothesis and the conclusion. A converse is valid if and only if the original conditional is valid and the hypothesis and conclusion are switched. The hypothesis "x < 0" and the conclusion "x5 < 0" are the two parts of the conditional statement "If x < 0, then x5 < 0."
Therefore, the converse of this statement is "If x5 < 0, then x < 0." This converse is correct since it is always valid. If x5 is less than zero, x must be less than zero because a negative number to an odd power is still negative.
know more about Converse
https://brainly.com/question/31918837
#SPJ11
Which percentage is the same as 3.21
Answers
Answer:
321%
Step-by-step explanation:
hope I helped Kkkkkkkk
ursesRead bar graphsBella counted the number of students who play various instruments in her school's marching band and graphedthe results.file48) 1 34032ASCNumber of students24As16MY80TATUSCoFlute Saxophone DrumsTromboneTrumpetMYInstrumentProWhich instruments did the same number of students play?ProChoose 2 answers:ТеаFluteTrombone

Answers
SOLUTION:
We are to find the instruments that same number of students play?
Considering the given bar-chart, 32 students played each of Saxophone and Drums.
Therefore the answer is Saxophone and Drums.
The graph of y=f(x) is shown below. What are all the real solutions of f(x)=0

Answers
Answer:
i don't have ideas
Given the function: f (x) = (3 x + 4) minus (2 minus x) Evaluate for f (5). a. 22 b. 15 c. 16 d. 30 Please select the best answer from the choices provided A B C D
Answers
Answer:
A.22 is the answer
Step-by-step explanation:
When it says "f(5)", it is basically saying that what is the y-value if the x-value is 5. To find the y-value, we need to substitute 5 in for the variables. I have provided you with the steps.

children should develop strategies for remembering the facts before they engage in drill and practice to develop fluency
Answers
Developing strategies for remembering facts is essential for children before they engage in drill and practice activities to develop fluency. By establishing these strategies, children can effectively learn, retain, and recall information, ultimately enhancing their performance during practice sessions.
Yes, it is important for children to develop strategies for remembering facts before engaging in drills and practice to develop fluency. By doing so, children can enhance their ability to recall information more quickly and accurately, making it easier for them to perform well on tests and assignments. Strategies such as visualizing, chunking, and using mnemonic devices can help children remember information more effectively. Once these strategies are established, drill and practice can then be used to further reinforce their understanding and speed up their recall time. This approach can ultimately lead to improved academic performance and a stronger foundation for learning.
Learn more about practice:
brainly.com/question/30423751
#SPJ11
the number of DVDs shipped to an online retailer was 20000 less that the previous year use an integer to describe the change in number of DVDs shipped
Answers
The number of DVDs shipped is, 20000 less that the previous year ,
Therefore, the integer -20000 can be used to describe the change.
After finding the fish you would like to take home to cook, you discover it cost $2 to wrap the fish and $4.50 per pound. Another vendor is selling another fish for a flat rate of $5 per pound. Set up an equation to determine how many pounds of fish would result in the same cost. Then, solve the equation.
Answers
Equation: 2 + 4.50x = 5x
Step by step
We know one vendor charges $2 + $4.50/#
We know one vendor charges $5/#
X = unknown # pound
Our equation will be separated by = sign because we are looking for when the price will equal
2 + 4.50x = 5x
Subtract 4.50x from both sides to isolate the variable
2 = .50x
Divide both sides by .50 to solve for x
X = 4 # fish
Substitute your x value (4) for x in your equation
4.50x4 + 2 = 5x4
20 = 20
They equal, problem solved!
the temperature was 88°F at 2pm the temperature decreases 4° per hour what time will the temperature be 72°f
Answers
Find the sum of the interior angle measures of the polygon.

Answers
Answer:
360°
Step-by-step explanation:
Sum of interior angles of polygon:Sum of interior angles of polygon = (n - 2) *180
n is the number of sides of the polygon.
= (4 - 2) *180
= 2 * 180
= 360°
Case Study - 1
Ajay want to celebrate his birthday party with his friends, he decided to have ice-cream as must in
the menu. The container is in the shape of a right circular cylinder having diameter 12 cm and height
15 cm is full of ice-cream. This ice - cream is to be filled into cones of height 12 cm and diameter
6 cm, having a hemispherical shape on the top. Answer the following after reading passage.
i) What is the capacity of cylindrical container?
ii)
Find the surface area of ice-cream cone calculated ?
iii)
Find the volume of 1 ice-cream?
iv)
Find the CSA of cylindrical container?
v)
Find the number of ice-cream cones can be filled ?
Answers
The volume and surface area of the ice cream cone are given by adding
the volume and surface area of the component parts.
Responses (approximate values)
i) 1,696.46 cm³
ii) 229.68 cm²
iii) 169.45 cm³
iv) 565.49 cm²
v) 10 cones
Which methods can be used to calculate the volume and surface area of the given figures?Given:
The diameter of the cylinder = 12 cm
Height of the cylinder, h = 15 cm
Height of the cone, h = 12 cm
Diameter of the cone, D = 6 cm
Shape of the cap of the cone = Hemispherical
i) The capacity of the container = The volume of the cylinder
Volume of a cylinder = Area of base × height
Radius of the cylinder, R = \(\mathbf{\dfrac{D}{2}}\)
Which gives;
\(R = \dfrac{12 \, cm}{2} = 6 \, cm\)
Volume of the cylinder, V = \(\pi \times R^2 \times h\)
V = π × (6 cm)² × 15 cm = 540·π cm³ ≈ 1,696.46 cm³ii) The surface area of a cone, \(A_c\) = π·r·(r + √(h² + r²))
Surface area of the hemisphere = 3·π·r²
Which gives;
Surface area of ice cream cone,\(A_{ch}\) = π·r·(r + √(h² + r²)) + 3·π·r²
Where;
r = The radius of the cone = \(\dfrac{6 \, cm}{2}\) = 3 cm
\(A_{ch}\) = π ×3 × (3 + √(12² + 3²)) + 3·π·3² ≈ 229.68
Surface area of ice cream cone,\(A_{ch}\) ≈ 229.68 cm²
iii) The volume of 1 ice-cream, \(V_{ic}\) = \(\frac{1}{3}\) × π × r² × 12 + \(\frac{2}{3}\) × π × r³
Which gives;
\(V_{ic}\) = \(\frac{1}{3}\) × π × 3² × 12 + \(\frac{2}{3}\) × π × 3³≈ 169.45
The volume of 1 ice-cream, \(V_{ic}\) = 169.45 cm³iv) The CSA of the cylindrical container is given as follows;
Curves Surface Area of a cylinder, CSA = 2·π·R·h
CSA = 2 × π × 6 cm × 15 cm ≈ 565.49 cm²v) The number of ice-cream cones, n, that can be filled is given as follows;
\(n = \dfrac{V}{V_{ic}}\)
\(n = \dfrac{1,696.46 \, cm^3}{169.45 \, cm^3/cone} \approx 10 \ cones\)
The number of ice-cream cones that can be filled ≈ 10 cones
Learn more about the volume of regular solids here:
https://brainly.com/question/13338580
use the midpoint rule with n = 4 to approximate the area of the region bounded by the graph of the function and the x-axis over the given interval. f(x) = x2 4x, [0, 4]
Answers
The approximate area of the region bounded by the graph of the given function and the x-axis over the interval [0, 4] is -12.5 square units.
What is the midpoint rule?
The midpoint rule is a numerical method used to approximate the definite integral of a function over an interval. It is based on approximating the area under the curve of the function using rectangles.
To approximate the area of the region bounded by the graph of the function\(f(x) = x^2 - 4x\) and the x-axis over the interval [0, 4] using the midpoint rule with n = 4, we can follow these steps:
1.Divide the interval [0, 4] into subintervals of equal width. Since n = 4, we will have four subintervals with a width of \(\frac{4 - 0}{ 4} = 1.\)
2.Find the midpoint of each subinterval. The midpoints for the four subintervals are 0.5, 1.5, 2.5, and 3.5.
3.Evaluate the function \(f(x) = x^2 - 4x\) at each midpoint. We get the following values:
\(f(0.5) = (0.5)^2 - 4(0.5)\\= -1.75\)
\(f(1.5) = (1.5)^2 - 4(1.5)\\= -3.75\)
\(f(2.5) = (2.5)^2 - 4(2.5)\\= -4.25\\ f(3.5) = (3.5)^2 - 4(3.5)\\ = -2.75\)
4.Multiply each function value by the width of the subintervals (1 in this case). We get the following products:
(-1.75)(1) = -1.75
(-3.75)(1) = -3.75
(-4.25)(1) = -4.25
(-2.75)(1) = -2.75
5.Sum up the products to approximate the area of the region. -1.75 + (-3.75) + (-4.25) + (-2.75) = -12.5
Therefore, the approximate area of the region bounded by the graph of the function \(f(x) = x^2 - 4x\) and the x-axis over the interval [0, 4] using the midpoint rule with n = 4 is -12.5 square units.
To learn more about the midpoint rule from the given link
brainly.com/question/30241651
#SPJ4
please answer this for me?

Answers
Answer:
n/a
Step-by-step explanation:
how does it feel
Consider the following Linear Programming Problem (LPP):
Maximize Z = 3x1 + 2x2 Subject to
x1 ≤ 4
x2 ≤ 6
3x1 + 2x2 ≤ 18
x1 ≥ 0, x2 ≥ 0
Answers
The given linear programming problem aims to maximize the objective function \(Z = 3x1 + 2x2\), subject to four constraints: x1 ≤ 4, x2 ≤ 6, 3x1 + 2x2 ≤ 18, and x1 ≥ 0, x2 ≥ 0.
The objective of linear programming is to optimize (maximize or minimize) a linear objective function while satisfying a set of linear constraints. In this case, the objective is to maximize \(Z = 3x1 + 2x2\).
The constraints in the problem define the feasible region, which is the set of all points that satisfy the constraints. The constraints state that x1 must be less than or equal to 4, x2 must be less than or equal to 6, and the linear combination \(3x1 + 2x2\) must be less than or equal to 18. Additionally, both x1 and x2 must be greater than or equal to zero.
To solve this linear programming problem, graphical methods or optimization algorithms such as the simplex method can be employed. The feasible region is determined by graphing the constraints and finding the overlapping region. The optimal solution is the point within the feasible region that maximizes the objective function.
The explanation of the solution, including the optimal values of x1 and x2, the maximum value of Z, and the graphical representation of the problem, can be provided based on the chosen method of solving the linear programming problem.
Learn more about Linear Programming problem (LPP) here:
https://brainly.com/question/29405467
#SPJ11
adding and subtracting fractions with unlike denominators worksheets pdf
Answers
A simple method for adding and subtracting fractions with unlike denominators:
Find a common denominator: The first step is to find a common denominator that is a multiple of both denominators. The smallest common denominator is usually the least common multiple (LCM) of the two denominators.
Convert the fractions to equivalent fractions with the common denominator: Once you have a common denominator, you can convert each fraction to an equivalent fraction with the same denominator by multiplying the numerator and denominator by the same number.
Add or subtract the numerators: Once both fractions have the same denominator, you can add or subtract the numerators to get the numerator of the resulting fraction.
Simplify the resulting fraction: Finally, simplify the resulting fraction by dividing both the numerator and denominator by their greatest common factor, if possible.
Here is an example:
To add 1/3 + 1/4, we first find a common denominator:
The LCM of 3 and 4 is 12, so we multiply both the numerator and denominator of each fraction by 4 to get 12/12 as the common denominator:
1/3 * 4/4 = 4/12
1/4 * 3/3 = 3/12
Next, we add the numerators:
4/12 + 3/12 = 7/12
Finally, we simplify the fraction:
7/12 = (7 ÷ 1) / (12 ÷ 1) = 7/12.
So the result is 7/12.
To know more about Fractions
https://brainly.com/question/78672
#SPJ4
A parallelogram is cut out of a 12 inch by 8 inch sheet of paper there are four right triangles remnats two have the dimensions 2 inches by 9 inches and the other two have the dimensions 3 inches by 6 inches
Answers
Answer:
96 in²
36 in²
60 in²
6.51 in
Step-by-step explanation:
Given that :
Dimension of paper = 12 in by 8 in
Dimension of right triangles :
2 in by 9 in ; 3 in by 6 in
Area of sheet of paper = 12 in * 8 in = 96 in²
Area of triangle = 1/2 base * height
Therefore, area of remnant right triangle :
2 * 1/2 * 2 * 9 = 18 in²
2 * 1/2 * 3 * 6 = 18 in²
Combined area of triangle left = 18in + 18in = 36 in²
Area of parallelogram = Area of sheet - Area of triangles left
Area of parallelogram = 96in² - 36in² = 60 in²
Base, b of parallelogram = 9.22 in
Area of parallelogram = base * altitude,h
60in² = 9.22h
h = 60 / 9.22 = 6.51 in
A 2-column table with 6 rows. The first column is labeled x with entries negative 4, negative 3, negative 2, negative 1, 0, 1. The second column is labeled f of x with entries negative 10, 0, 0, negative 4, negative 6, 0.
Which is a y-intercept of the continuous function in the table?
(0, –6)
(–2, 0)
(–6, 0)
(0, –2)
Answers
Answer:
(0, –6)
Step-by-step explanation:
The y-intercept is when x = 0
so options
(–2, 0)
(–6, 0)
are incorrect
According to the table, when x = 0, f(x) = -6

a family of 4 went to a lacrosse game and spent a total of $74. they each had a hot dog, popcorn, and a soda. a hot dog cost $3, popcorn costs $1.50 and a soda cost $2. what was the cost of each ticket?
Answers
Answer:
12$
Step-by-step explanation:
74 - 4(1.50+3+2) = 48
48 / 4 = 12
can someone help me out please ?
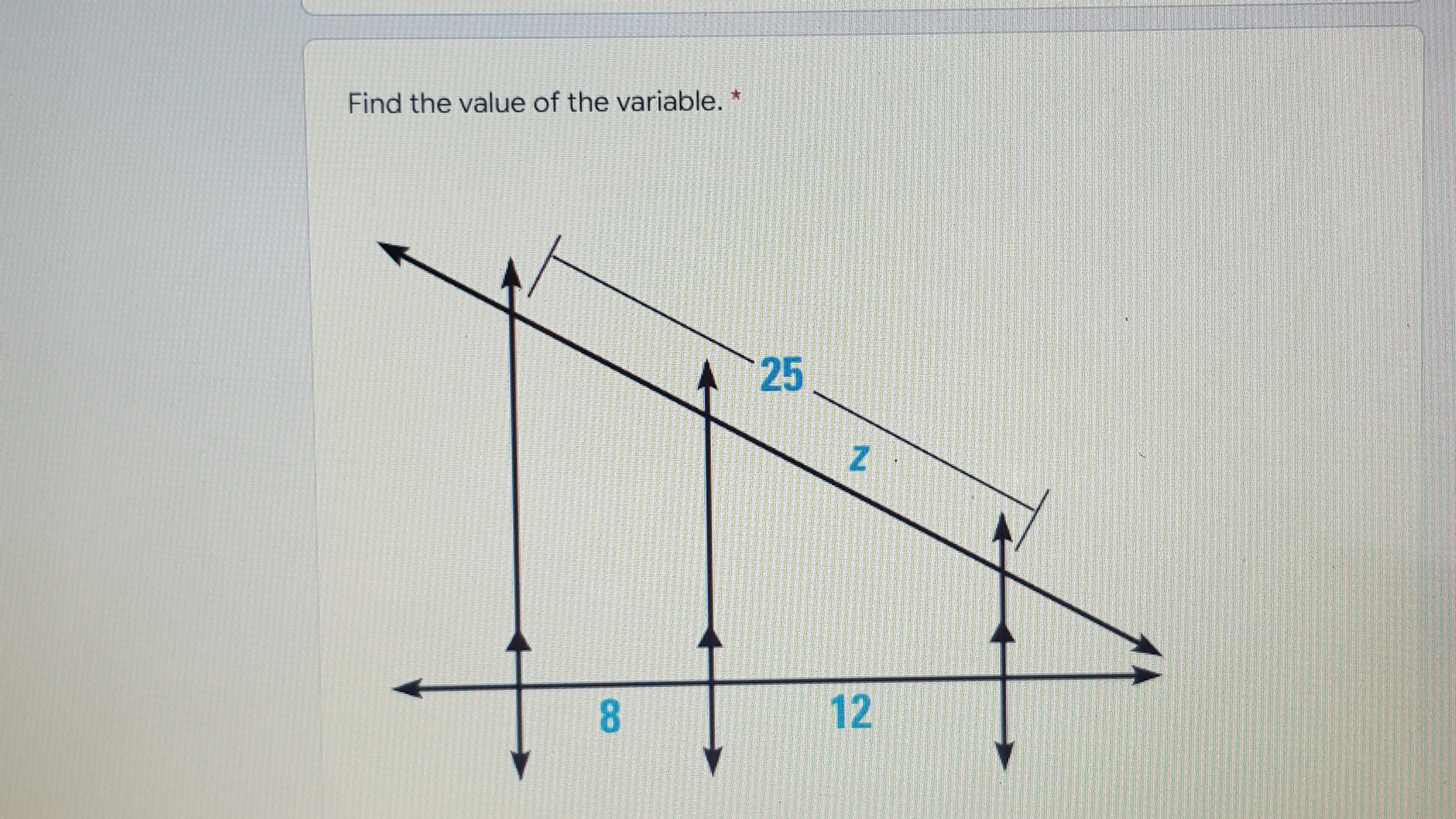
Answers
Answer:
\(8 + x = 25 \\ x = 25 - 8 \\ 17\)
please hurry if answer is correct i will give brainlyyyyest thx
In this task, you will calculate the area of a complicated shape by splitting it into simpler shapes. Cut out shape C. Shape C is not a regular shape, so you cannot directly apply a formula to find its area. Split shape C into simpler shapes whose areas you can find by applying formulas. List the simple shapes into which you divided shape C, and measure their sides. Write all the measurements in inches.
Answers
Answer:
i could only get part one done
Step-by-step explanation:
Perimeter is a measurement of the distance around a shape and area gives us an idea. Understanding how much space you have and learning how to fit shapes ... If the shape is a polygon, then you can add up all the lengths of the sides to find the perimeter. ... You can write “in2” for square inches and “ft2” for square feet
What is the unknown digit?

Answers
Answer: 2
5542 divided by 17 is 2
