Given the solid Ethat lies between the cone z2 = x2 + y2 and the sphere x2 + y2 + (z + 2)2 = 2 a) Set up the triple integrals that represents the volume of the solid E in the rectangular coordinate system b)Set up the triple integrals that represents the volume of the solid E in the cylindrical coordinate system c) Evaluate the volume of the solid E
Answers
a) The volume of the solid E in rectangular coordinate system is given by: \($$\iiint_{E}\) dx dy dz = \(\int_{-2}^{2} \int_{0}^{\sqrt{z^2}} \int_{-\sqrt{z^2 - y^2}}^{\sqrt{z^2 - y^2}} dx dy dz$$\)
b) The volume of the solid E in cylindrical coordinate system is given by: \($$\iiint_{E} \rho d\rho d\theta dz = \int_{0}^{2} \int_{0}^{\frac{\pi}{2}} \int_{0}^{\sqrt{4 - z^2}} \rho d\rho d\theta dz$$\)
c) The volume of the solid E is 11π/3.
a) The solid E that lies between the cone z² = x² + y² and the sphere x² + y² + (z + 2)² = 2.
Volume of solid E in rectangular coordinate systemLet the limits of x, y, z be X, Y, Z respectively.
The limits of X:
From the equation, z² = x² + y²
Z² = X² + Y²
X² = Z² - Y²
Let Z = 0, then X² = - Y² which is impossible. Therefore, Y can take any value such that Y < Z.
The limits of Y:
From the equation, z² = x² + y²
Z² = X² + Y²
Y² = Z² - X²
Let Z = 0, then Y² = - X² which is impossible. Therefore, X can take any value such that X < Z.
Limits of Z:
From the equation x² + y² + (z + 2)² = 2z² + 4z + 8 = 2(Z + 1)² + 6
The limits of z are Z < 2 and Z > - 2.
Volume in rectangular coordinate system:
\($$\iiint_{E}\) dx dy dz = \(\int_{-2}^{2} \int_{0}^{\sqrt{z^2}} \int_{-\sqrt{z^2 - y^2}}^{\sqrt{z^2 - y^2}} dx dy dz$$\)
b) Volume of solid E in cylindrical coordinate system
Let the limits of ρ, θ, z be R, Θ, Z respectively.
The limits of R:
From the equation, z² = ρ² cos²θ + ρ² sin²θ
Z² = ρ²
Rho² = Z²/ cos²θ + sin²θ
Rho = Z/ cosθ
Let Z = 0, then Rho = 0. Therefore, R can take any value such that 0 ≤ R < 2.
Limits of Θ:
From the equation, z² = ρ² cos²θ + ρ² sin²θ
Z² = ρ² sin²θ
Theta² = tan⁻²(Z²/ ρ²)
Let Z = 0, then Θ = 0. Therefore, Θ can take any value such that 0 ≤ Θ ≤ π/2.
Limits of Z:
From the equation x² + y² + (z + 2)² = 2z² + 4z + 8 = 2(Z + 1)² + 6
The limits of Z are -2 ≤ Z < 2.
Volume in cylindrical coordinate system:
\($$\iiint_{E} \rho d\rho d\theta dz = \int_{0}^{2} \int_{0}^{\frac{\pi}{2}} \int_{0}^{\sqrt{4 - z^2}} \rho d\rho d\theta dz$$\)
c) Evaluation of the volume of solid E:
Using rectangular coordinate system, the volume of solid E is
\($$\iiint_{E} dx dy dz\) = \(\int_{-2}^{2} \int_{0}^{\sqrt{z^2}} \int_{-\sqrt{z^2 - y^2}}^{\sqrt{z^2 - y^2}} dx dy dz$$$$\)
\(=\int_{-2}^{2} \int_{0}^{\sqrt{z^2}} [x]_{-\sqrt{z^2 - y^2}}^{\sqrt{z^2 - y^2}} dy dz$$$$=\int_{-2}^{2} \int_{0}^{\sqrt{z^2}} 2\sqrt{z^2 - y^2} dy dz$$$$=\int_{-2}^{2} \left[-\frac{1}{2}(z^2 - y^2)^{3/2}\right]_{y=0}^{y=\sqrt{z^2}} dz$$$$=\int_{-2}^{2} \frac{1}{2}z^3 dz = 0$$\)
Therefore, the volume of solid E using rectangular coordinate system is 0.
Using cylindrical coordinate system, the volume of solid E is
\($$\iiint_{E} \rho d\rho d\theta dz = \int_{0}^{2} \int_{0}^{\frac{\pi}{2}} \int_{0}^{\sqrt{4 - z^2}} \rho d\rho d\theta dz$$$$=\int_{0}^{2} \int_{0}^{\frac{\pi}{2}} \left[\frac{\rho^2}{2}\right]_{0}^{\sqrt{4 - z^2}} d\theta dz$$$$=\int_{0}^{2} \int_{0}^{\frac{\pi}{2}} 2 - \frac{z^2}{2} d\theta dz$$$$=\int_{0}^{2} \left[2\theta - \frac{\theta z^2}{2}\right]_{\theta = 0}^{\theta = \frac{\pi}{2}} dz$$$$=\int_{0}^{2} \pi - \frac{\pi z^2}{4} dz = \frac{11\pi}{3}$$\)
Therefore, the volume of solid E using cylindrical coordinate system is 11π/3.
To know more about cylindrical coordinate system, refer to the link below:
https://brainly.com/question/32517783#
#SPJ11
Related Questions
What was the purpose of Lend-Lease ?
Answers
The purpose of Lend-Lease was to provide military aid to countries fighting against the Axis powers during set World War II.
The purpose of Lend-Lease was to provide military aid to countries fighting against the Axis powers during World War II. The program was enacted by the United States in 1941 and allowed the US to provide war materials to its allies without requiring repayment. It was a major factor in the Allied victory, as it allowed the US to supply its allies with much needed war material and resources. The US provided a variety of goods, including food, oil, weapons, and tanks. It also supplied the Soviet Union with millions of tons of military equipment and supplies. Lend-Lease was instrumental in helping the Allies win the war, as it allowed them to gain a huge advantage over the Axis powers by providing essential supplies and resources.
Learn more about set here
https://brainly.com/question/12979762
#SPJ4
PLEASE HELP IM FAILING MATH IT IS 6th GRADE ALGEBRA
Answers
Answer:
1a, 2c, 3e, 4b, 5f, 6g
Step-by-step explanation:
i dont see the answer for 6, so i'm going with g
Answer:
1.A 2.C 3.E 4.B 5.F 6.G
Step-by-step explanation:
can i get brainliest plz
Only an answer please please
Answers
Answer: 41
Step-by-step explanation: r= 3c+ 5
3 (12) +5 36+5= 41
Answer:
B 35
Step-by-step explanation:
the value goes up by six in each box
Victor just bought a new television for $682.00. He made a down payment of $55.00 and will pay monthly payments of $33.00 until it is paid off. How many months will Victor be paying? (Assume that Victor pays no interest.)
Answers
Answer:
19 months
Step-by-step explanation:
First off 682- 55 = 627. 627/33 = 19
what is 100x100x200x1x2000x10000,000x40000x1000002x0000003xxxxxxxxxxxx000000
Answers
Answer:16.e+6.18
Step-by-step explanation:
wich of the following numbers are greater than -185/100 -1.08190/100-35/20
Answers
-185/100 = -1.85
a) -1.08 this number id greater than -1.85
b) 190/100 = 1.9 this number is greater than -1.85
c) -35/20 = -1.75 this number is greater than -1.85
All these numbers are greater than -185/100
How many solutions does the system of equations below have? y = 7 6 x + 6 7 y = 9 2 x − 4 9
Answers
Answer:
Im not sure what type of solution you are looking for. You should be more specific. Though I will still give you some helpful solutions and you use the one you need.
Step-by-step explanation:
Factored: y=168x+67y-49
Solved for Y; -28x/11 + 49/66
Solved for X: -11y/28 + 7/24
X and Y intercepts:
X=( 7/24, 0 )
Y= ( 0, 49/66 )
I hope these answers help. Next time be more specific to what your looking for and make sure your equation is written correctly.
3(-2 - n) = -9 -4n answer
Answers
Answer:
n = -3
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDASEquality PropertiesStep-by-step explanation:
Step 1: Define equation
3(-2 - n) = -9 - 4n
Step 2: Solve for n
Distribute 3: -6 - 3n = -9 - 4nAdd 4n to both sides: -6 + n = -9Add 6 to both sides: n = -3Step 3: Check
Plug in n to verify it's a solution.
Substitute: 3(-2 - -3) = -9 - 4(-3)Simplify: 3(-2 + 3) = -9 - 4(-3)Add: 3(1) = -9 - 4(-3)Multiply: 3 = -9 + 12Add: 3 = 3when these equations are added together, what will the overall equation be? assume that no equations need to be reversed.
Answers
On adding the provided equations, 4x +7y= 17 and 9x + 13y = 46 the resultant equation we will be getting is 13x + 20y = 63.
In order to perform addition of two equations together, we are needed to add the left-hand side of each equation and the right-hand side of each equation separately. This gives us:
(4x + 7y) + (9x + 13y) = 17 + 46
Combining like terms on both the sides, we will be getting ,
13x + 20y = 63
Therefore, from the above calculations this inference can be drawn that the overall equation is calculated to be 13x + 20y = 63.
Learn more about Equations :
https://brainly.com/question/14550031
#SPJ4
The complete question is :
4x +7y= 17
9x + 13y = 46
when these equations are added together, what will the overall equation be? assume that no equations need to be reversed.
Describe what the line on a graph would look like if it had a constant positive rate ?
Answers
Horizontal = —
Vertical = |
Two congruent ellipses are perpendicular to each other. Squares fill the gaps between the two ellipses as shown. Show that the side of the square equals half the minor axis of the ellipse.
Answers
The side of the square equals half the minor axis of the ellipse.
To show that the side of the square is half the minor axis of the ellipse, we must prove that the angles of the ellipses and the squares are congruent. To do this, we must first draw in the diagonals of the square, which will form two additional isosceles triangles.
Since the ellipses are perpendicular, the angles of the ellipses and the squares will be the same. Since the angles of the isosceles triangles are equal, the side of the square must be equal to half of the minor axis of the ellipse. Therefore, the side of the square is equal to half of the minor axis of the ellipse.
For more questions like Minor axis click the link below:
https://brainly.com/question/29054958
#SPJ4
Who got my back on this question
Answers
Answer:
It's prime, the others are for English.
Step-by-step explanation:
the average of 8 girls is 15 and the average of 6 girls is 13 find the average of the other two girls with equal age
Answers
Answer:
21
Step-by-step explanation:
Since the girls have the same age, let their age be x.
Then, their average is
\(\frac{x+x}{2} = \frac{2x}{2} = x\)
Let \(S_{i}\) denote the age of 'i' girls.
Then, \(S_{8} = S_{6} + x + x - eq(1)\)
Also, we have,
\(\frac{S_{8}}{8} =15 - eq(2)\)
\(\frac{S_{6}}{6} =13 - eq(3)\)
Then eq(2):
(from eq(1) and eq(3))
\(\frac{S_{6} + 2x}{8} =15\\\\\frac{13*6 + 2x}{8} = 15\\\\78+2x = 120\\\\2x = 120-78\\\\x = 21\)
The average of the other two girls with equal age is 21
6. You hope to buy a $10,000 car in cash in five years. Your bank is offering aspecial account that pays 6.4% interest compounded continuously. Howmuch money do you need to invest in this account now in order to buy thecar in five years?
Answers
Let individual invest P in account.
The formula for the amount is,
\(A=P(1+\frac{r}{100})^t\)Determine the value of P for A = 10,000, r = 6.4% anf t = 5.
\(\begin{gathered} 10000=P(1+\frac{6.4}{100})^5 \\ 10000=P(1+0.064)^5 \\ P=\frac{10000}{1.3636664} \\ =7333.1718 \\ \approx7333.2 \end{gathered}\)Thus individual invest $7333.2 in account to buy car in five years.
10 On some days, Jardon travels from home directly to his work. On other days, Jardon visits with his
friend on his way to work.
Work
120 yards
Home
240 yards
Friend's House
Approximately how much farther would Jardon travel by walking from
his home to his friend's house
and then from his friend's house to work than he would travel by walking from his home directly to work?
F 92 yos
G 120 yds
H268 yds
J 360 yds
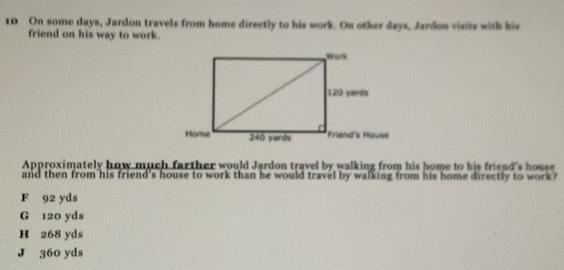
Answers
Answer:
Jardon will walk 92 yards more to reach work via his friend's house.
Step-by-step explanation:
Distance between Jardon's home and his friend's home = 240 yards
Distance between friend's house and work = 120 yards
To measure the distance between Jardan's home and work directly we will use the Pythagoras theorem,
Distance from Jardon's home to work directly = \(\sqrt{(240)^2+(120)^2}\)
= 120√5
= 268.33 yards
Distance between Jardon's house via his friend's house = 240 + 120
= 360 yards
Difference between both the ways to reach the work = 360 - 268.33
= 91.67
≈ 92 yards
Therefore, Jardon will walk 92 yards more to reach work via his friend's house.
0.2w – 5 = 13
Solve pleaseeee I'm struggling
Answers
Answer:
90
Step-by-step explanation:
Jessica's weekly math assignment has 40 problems. She solved 3/8 of them on Monday and 8 on Tuesday. what is the total number of questions she completed
Answers
Answer:
She completed 23 questions
Step-by-step explanation:
3/8(40/1) = 120/8 Divide 120 by 8 to get 15
15 + 8 = 23
help me out pleaseeeeeeeeeeeeeeeeeee
Answers
Answer:
3 and 5
Step-by-step explanation:
Find the inverse of the following matrix:
121
302
182
The inverse of this matrix is not defined
0131
208
122
Answers
The inverse of the given matrix is not defined.
To find the inverse of a matrix, we need to check if the matrix is invertible or non-singular. For a square matrix to be invertible, its determinant must be non-zero.
Let's calculate the determinant of the given matrix:
Det(Matrix) = (1 * 0 * 2) + (2 * 2 * 1) + (1 * 3 * 8) - (2 * 0 * 1) - (1 * 2 * 8) - (1 * 3 * 0)
= 0 + 4 + 24 - 0 - 16 - 0
= 12
Since the determinant of the given matrix is non-zero (12 ≠ 0), it implies that the matrix is invertible.
Next, we can proceed to find the inverse of the matrix by using the formula:
Matrix^(-1) = (1/Det(Matrix)) * Adjoint(Matrix)
However, before calculating the adjoint of the matrix, let's check for any possible errors in the matrix elements. The elements of the matrix you provided are not consistent, and it seems there might be a mistake. The matrix you provided (121, 302, 182) does not conform to the standard 3x3 matrix format.
In conclusion, based on the given matrix, the inverse is not defined. Please make sure to provide a properly formatted 3x3 matrix to find its inverse.
Know more about the inverse of a matrix click here:
https://brainly.com/question/28097317
#SPJ11
question shown in the photo, don’t mind the unfinished answer in the text box
Answers
Since the production of y must exceed the production of x by at least 100 units, we can write a second inequality:
\(y\ge x+100\)Looking at the function P, we can see that the coefficient multiplying y is greater than the coefficient multiplying x, therefore increasing y instead of x will have a bigger increase in P.
But from the inequality x + 2y <= 1400, we can see that the "cost" of producing y is two times the "cost" of producing x, that is, for one y produced, we could have produced 2x instead.
The coefficient of y is greater, but it's not more than 2 times greater, therefore it's better to produce x than y.
Since y needs to be at least 100 more than x, let's choose the minimum amount of y to satisfy the inequalities:
\(\begin{gathered} x+2y\le1400\to x\le1400-2y \\ x+100\le y\to x\le y-100 \\ \\ 1400-2y=y-100 \\ y+2y=1400+100 \\ 3y=1500 \\ y=500 \\ x+100=500 \\ x=400 \end{gathered}\)Therefore the values of x and y that give the maximum profit are x = 400 and y = 500.
Graphing the two inequalities, we have:
The feasible region is the intersection region (between red and blue).
The vertices are:
(0, 100), (400, 500), (0, 700).
Calculating the maximum profit (with vertex (400, 500)), we have:
\(\begin{gathered} P=14\cdot400+22\cdot500-900 \\ P=5600+11000-900 \\ P=15700 \end{gathered}\)Therefore the production that yields the maximum profit is x = 400 and y = 500, and the maximum profit is P = 15700.
Sometimes linear equations are written in forms other than y=mx+b . One common form looks like Ax+By=C .When you see an equation like this, you can find the slope and y-intercept by solving the equation for y, rewriting it into slope-intercept form.Rewrite 6x+2y=6 into slope-intercept form by solving for y.y=______From that we can see that:m=____b=____
Answers
Okay, here we have this:
Considering the provided equation, we are going to rewriting it into slope-intercept form. So we obtain the following:
6x+2y=6
2y=-6x+6
y=(-6x+6)/2
y=-3x+3
Finally we obtain that the equation of the line is slope-intercept form is y=-3x+3. Then replacing in y=mx+b, we have:
y=-3x+3
y=mx+b
Then, m=-3 and b=3.
Hi, please can you help with this graph equation problem?
The gradient is 3 which passes through (1,10)
Find the equation of the line
Answers
y = mx + c
Where the m is gradient, the y is the y-axis, the x is the x-axis and the c is the y-intercept.
Given gradient to be 3, the coordinate (1,10). Let’s substitute the values into the equation.
Let m = 3
y = 10
x = 1
10 = 3(1) + c
Given this equation we have to solve for c.
10 = 3(1) + c
10 = 3 + c
10 - 3 = c
7 = c
Therefore, c which is the y-intercept is 7.
Now we rewrite the equation of the line with the c value.
y = 3x + 7
Help I give 20 points answer ASAP
Answers
Answer:
-1
Step-by-step explanation:
please help 100 points wrong answers and links will be reported
Circle and Show!
(4 points each: 1 for the correct answer and 3 for supporting work!)
For numbers 8 -12, check the box next to the correct answer and type your work for that
problem.
Work must support your answer selection for credit!
Answers
Please find attached herewith the solutions of your questions.
Hope it helps.
If you have any query, feel free to ask.
Answer:
\(\textsf{8.} \quad \textsf{B.}\;8x^3y\)
\(\textsf{9.} \quad \textsf{D.}\;81x^8\)
\(\textsf{10.} \quad \textsf{A.}\;10t^{-7}\)
\(\textsf{11.} \quad \textsf{C.}\;\dfrac{3m^2}{x^3}\)
\(\textsf{12.} \quad \textsf{B.}\;\dfrac{1}{3m^9}\)
Step-by-step explanation:
Exponent Rules
\(\textsf{Product rule}: \quad a^b \cdot a^c=a^{b+c}\)
\(\textsf{Power rule}: \quad (a^b)^c=a^{bc}\)
\(\textsf{Quotient rule} \quad \dfrac{a^b}{a^c}=a^{b-c}\)
\(\textsf{Power of a Product rule}: \quad (ab)^c=a^{c} \cdot b^c\)
\(\textsf{Negative exponent rule} \quad a^{-n}=\dfrac{1}{a^n}\)
Question 8\(\begin{aligned}\left(2x^2y^3\right)\left(4xy^{-2}\right)&=2 \cdot 4 \cdot x^2 \cdot x \cdot y^3 \cdot y^{-2}\\&=8\cdot x^{(2+1)}\cdot y^{(3-2)}\\&=8 \cdot x^3 \cdot y^1\\&=8x^3y\end{aligned}\)
Question 9\(\begin{aligned}\left(3x^2\right)^4&=3^4 \cdot (x^2)^4\\&=81 \cdot x^{(2 \cdot 4)}\\&=81x^8\end{aligned}\)
Question 10\(\begin{aligned}5t^{-2} \cdot 2t^{-5}&=5 \cdot 2 \cdot t^{-2} \cdot t^{-5}\\&=10 \cdot t^{(-2-5)}\\&=10t^{-7}\end{aligned}\)
Question 11\(\begin{aligned}\dfrac{6m^{10}x^4}{2m^8x^7}&=\dfrac{6}{2} \cdot \dfrac{m^{10}}{m^8} \cdot \dfrac{x^4}{x^7}\\\\&=3 \cdot m^{(10-8)} \cdot x^{(4-7)}\\\\&=3m^2x^{-3}\\\\&=\dfrac{3m^2}{x^3}\end{aligned}\)
Question 12\(\begin{aligned}\dfrac{m^{-3}}{3m^6}&=\dfrac{1}{3} \cdot \dfrac{m^{-3}}{m^{6}}\\\\&=\dfrac{1}{3} \cdot m^{(-3-6)}\\\\&=\dfrac{1}{3} \cdot m^{-9}\\\\&=\dfrac{1}{3m^9}\end{aligned}\)
What is the sum of the geometric sequence 2, 8, 32, if there are 8 terms?
Answers
Answer:
43690
Step-by-step explanation:
hope u understand it
Pls solve with all steps
Answers
The results of the expressions involving logarithms are listed below:
Case 1: 1 / 2
Case 2:
Subcase a: 0
Subcase b: 11 / 2
Subcase c: - 11 / 2
How to simplify and evaluate expressions involving logarithmsIn this problem we have a case of an expression involving logarithms that must be simplified and three cases of expressions involving logarithms that must be evaluated. Each case can be solved by means of the following logarithm properties:
㏒ₐ (b · c) = ㏒ₐ b + ㏒ₐ c
㏒ₐ (b / c) = ㏒ₐ b - ㏒ₐ c
㏒ₐ cᵇ = b · ㏒ₐ c
Now we proceed to determine the result of each case:
Case 1
㏒ ∛8 / ㏒ 4
(1 / 3) · ㏒ 8 / ㏒ 2²
(1 / 3) · ㏒ 2³ / (2 · ㏒ 2)
㏒ 2 / (2 · ㏒ 2)
1 / 2
Case 2:
Subcase a
㏒ [b / (100 · a · c)]
㏒ b - ㏒ (100 · a · c)
㏒ b - ㏒ 100 - ㏒ a - ㏒ c
3 - 2 - 2 + 1
0
Subcase b
㏒√[(a³ · b) / c²]
(1 / 2) · ㏒ [(a³ · b) / c²]
(1 / 2) · ㏒ (a³ · b) - (1 / 2) · ㏒ c²
(1 / 2) · ㏒ a³ + (1 / 2) · ㏒ b - ㏒ c
(3 / 2) · ㏒ a + (1 / 2) · ㏒ b - ㏒ c
(3 / 2) · 2 + (1 / 2) · 3 + 1
3 + 3 / 2 + 1
11 / 2
Subcase c
㏒ [(2 · a · √b) / (5 · c)]⁻¹
- ㏒ [(2 · a · √b) / (5 · c)]
- ㏒ (2 · a · √b) + ㏒ (5 · c)
- ㏒ 2 - ㏒ a - ㏒ √b + ㏒ 5 + ㏒ c
- ㏒ (2 · 5) - ㏒ a - (1 / 2) · ㏒ b + ㏒ c
- ㏒ 10 - ㏒ a - (1 / 2) · ㏒ b + ㏒ c
- 1 - 2 - (1 / 2) · 3 - 1
- 4 - 3 / 2
- 11 / 2
To learn more on logarithms: https://brainly.com/question/30226560
#SPJ1
The thesis statement, the theme or central idea of a speech, should be expressed as.
Answers
0.2 is what percent of 1 3/5
Answers
Answer:
12.5%
Step-by-step explanation:
0.2 of 1.6 is 12.5%. (0.2/1.5=12.5% or 0.125)
Which ONE of the following is NOT the critical point of the function f(x,y)=xye-(x² + y²)/2?
A. None of the choices in this list.
B. (0,0).
C. (1,1).
D. (-1,-1).
E. (0.1).
Answers
The critical point of the function f(x,y) = xy*e^(-(x^2 + y^2)/2) is (0,0). The critical points of a function occur where the gradient is zero or undefined.
To find the critical points of f(x,y), we need to calculate the partial derivatives with respect to x and y and set them equal to zero.
Let's find the partial derivatives:
∂f/∂x = ye^(-(x^2 + y^2)/2) - xy^2e^(-(x^2 + y^2)/2)
∂f/∂y = xe^(-(x^2 + y^2)/2) - xy^2e^(-(x^2 + y^2)/2)
Setting both partial derivatives to zero, we have:
ye^(-(x^2 + y^2)/2) - xy^2e^(-(x^2 + y^2)/2) = 0 ...(1)
xe^(-(x^2 + y^2)/2) - xy^2e^(-(x^2 + y^2)/2) = 0 ...(2)
From equation (2), we can simplify it as:
x = xy^2 ...(3)
Plugging this into equation (1), we get:
ye^(-(x^2 + y^2)/2) - (xy^2)^2e^(-(x^2 + y^2)/2) = 0
ye^(-(x^2 + y^2)/2) - x^2y^4e^(-(x^2 + y^2)/2) = 0
Factoring out ye^(-(x^2 + y^2)/2), we have:
ye^(-(x^2 + y^2)/2)(1 - xy^2e^(-(x^2 + y^2)/2)) = 0
This equation holds true if either ye^(-(x^2 + y^2)/2) = 0 or 1 - xy^2e^(-(x^2 + y^2)/2) = 0.
The first equation, ye^(-(x^2 + y^2)/2) = 0, implies y = 0.
The second equation, 1 - xy^2e^(-(x^2 + y^2)/2) = 0, implies x = 0 or y = ±1.
Considering these results, we can see that the only critical point that satisfies both equations is (0,0). Therefore, (0,0) is the critical point of the function f(x,y)=xye^(-(x^2 + y^2)/2).
To know more about critical points, refer here:
https://brainly.com/question/31308189#
#SPJ11
the last digit of the heights of statistics students were obtained as part of an experiment conducted for a class. use the following frequency distribution to construct a histogram. what can be concluded from the distribution of the digits? specifically, do the heights appear to be reported or actually measured?
Answers
The frequency distribution of the digits indicates that the heights were reported rather than actually measured. This is because the frequency of the digits is not evenly distributed, which would be expected for a set of actual measurements.
Frequency Distribution:
Digit Frequency
0 3
1 5
2 9
3 5
4 3
5 4
6 4
7 4
8 2
9 1
From the distribution of the digits, it appears that the heights were reported rather than actually measured. This is because the frequency of the digits is not evenly distributed, which would be expected for a set of actual measurements.
The frequency distribution of the digits indicates that the heights were reported rather than actually measured. This is because the frequency of the digits is not evenly distributed, which would be expected for a set of actual measurements. For example, the frequency of the digit '2' is more than twice as high as the frequency of the digits '1' and '3', which is not likely to occur in a set of actual measurements.
Learn more about distribution here
https://brainly.com/question/5637942
#SPJ4