Answers
Answer:
-3 I think...
Step-by-step explanation:
y=mx+b. where m is the slope, since -3 is the value for m, it is the slope
Related Questions
I need some help ? Does anyone know this:)I’m new too this thats why im asking loll

Answers
Answer:
6
Step-by-step explanation:
Answer: 9 in
Step-by-step explanation: area = (base x height)/ 2 You multiply base (6) times height (3), and then divide it by 2.
NEED HELP!! ILL MARK YOURE ANSWER BRAINLIST.
1) In 2005 the number of seniors at Falcon decreased by 63 students over the 9 month school year. If the decrease was the same over the entire 9 months, write the monthly decrease as a quotient of integers and find the monthly decrease. please show you're work.
Answers
Answer
9
Step-by-step explanation:
Divide 63 by 9 months
7 students per month
63 / 9 = 7
Would it be Survey equity? If not please explain
Which of the following is a better predictor of future equity risk premium? Implied Equity Risk Premium Historical geometric average equity risk premium Historical arithmetic average equity risk premi
Answers
The Implied Equity Risk Premium (ERP) is generally considered a better predictor of future equity risk premium
Implied Equity Risk PremiumWhat is Implied Equity Risk Premium?Implied Equity Risk Premium is derived from the current market prices of stocks and other securities. It represents the difference between the expected rate of return on equities and the risk-free rate of return. Investors' expectations about future returns are embedded in market prices, so the implied ERP reflects the collective wisdom and expectations of market participants. It takes into account current market conditions, investor sentiment, and other relevant factors, making it a forward-looking indicator.
On the other hand, historical geometric average and historical arithmetic average equity risk premium are calculated based on past performance data. While historical averages provide valuable insights into the past behavior of equity risk premium, they may not fully capture the changing dynamics of the market or reflect future expectations.
Learn more about implied ERP at
https://brainly.com/question/31829257
#SPJ4
The midpoint of AB is M (5,5). If the coordinates of A are (7, 8), what are the
coordinates of B?
Answers
Answer:
(3,2) just use a slope triangle (over 2 up 3) and do it in reverse
what is the measure of each angle in a regular quadrilateral?
Answers
Answer:
90°
Step-by-step explanation:
a regular polygon is equiangular, angles are equal.
a quadrilateral has 4 sides
the sum of the 4 angles in a quadrilateral = 360° , then
each angle = 360° ÷ 4 = 90°
Help help help help help

Answers
Choose the correct plural noun.
The ______ flowed, completing the circuit.
Choose 1 answer:
(Choice A)
A
electrae
(Choice B)
B
electrons
(Choice C)
C
electromena
Answers
Answer:electrons
Step-by-step explanation:
Simplify: x
\(x { }^{2} - 3x + 2 \ \div x {}^{2} - 4\)
x² - 4
4
Answers
Answer:
\(\frac{x-1}{x+2}\)
Step-by-step explanation:
simplifying the equation: \(x^2-3x+2/x^2-1\)
1) Rewrite the equation so it's easier to understand:
\(\frac{x^2-3x+2}{x^2-4}\)
2) factor \(x^2-3x+2\):
\(x^2-3x+2\) \(=> (x-1)(x-2)\)
3) factor \(x^2-4\):
\(x^2-4 => (x+2)(x-2)\)
Meaning: \(\frac{(x-1)(x-2)}{(x+2)(x-2)}\)
4) Cancel the common factor: \((x-2)\) from the numerator and the denominator:
\(=\frac{x-1}{x+2}\)
Evaluate the expression for n=-4
n-1
Answers
Answer:
Step-by-step explanation:
Step 1: Add 4n to both sides.
n+4n=−4n−1+4n
5n=−1
Step 2: Divide both sides by 5.
5n
5
=
−1
5
n=
−1
5
Solve:
5(n — 3) = 30
Answers
Answer:
n = 9
Step-by-step explanation:
5(n-3) = 30
Expand the brackets. (Multiply n by 5 then multiply -3 by 5.)
5n-15 = 30
Isolate 5n.
5n = 30+15
Evaluate.
5n = 45
Find n.
n = 45 ÷ 5
n = 9
Answer:
n = 9
Step-by-step explanation:
1) divide both sides by 5 to cancel it out
(n-3=6)
2) add 3 to each side to cancel out the -3
(n=9)
You could factor the 5 to get 5n-15=30 but dividing by 5 just makes the number easier
What’s the answer to c and d!!!

Answers
Answer:
Step-by-step explanation:
Determine the slope of the line represented by y=5x-7 ?
Answers
Step-by-step explanation:
that is totally easy.
in the slope intercept form of a line equation the factor of x is always the slope.
in general
y = ax + b
a = the slope.
so, in our case here
y = 5x - 7
5 is the slope.
and -7 is the y intercept (at what point does the line intercept the y-axis; that is the y value when x = 0).
A small fruit basket with 6 apples and 6 oranges costs $7.50. A different fruit basket with 10 apples and 5 oranges costs $8.75. If x is the cost of one apple and y is the cost of one orange, the system of equations below can be used to determine the cost of one apple and one orange.
6x+6y=7.50
10x+5y=8.75
What is the cost of one apple?
0.25
0.5
0.75
1.00
also to whomever reading ths, HAVE A GREAT DAY!!! go drink some water and take a break too!! <3
Answers
(and .75 for an orange)
i need help with this asap
dexide whether pait of angles
1 and 2
4 and 3
5 and 6
arw alternate interior angles
alternate exterior angles
corresponding anglws
same side intetior angles

Answers
Answer:
1 and 2 is corresponding angles
4 and 3 is alternate interior angles
5 and 6 corresponding angles
1. Solve for the unknown in each triangle. Round each answer to the nearest tenth.

Answers
The values of the missing sides are;
a. x = 35. 6 degrees
b. x = 15
c. x = 22. 7 ft
d. x = 31. 7 degrees
How to determine the valuesTo determine the values, we have;
a. Using the tangent identity;
tan x = 5/7
Divide the values
tan x = 0. 7143
x = 35. 6 degrees
b. Using the Pythagorean theorem
x² = 9² + 12²
find the square
x² = 225
x = 15
c. Using the sine identity
sin 29= 11/x
cross multiply the values
x = 11/0. 4848
x = 22. 7 ft
d. sin x = 3.1/5.9
sin x = 0. 5254
x = 31. 7 degrees
Learn more about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
Mark drew a regular octagon with side lengths of 10 inches. He divided the octagon into two identical trapezoids and a rectangle. He measured the height of one of the trapezoids to be 7 inches, and the width of the rectangle to be 24 inches. Find the area of the octagon.
Answers
Answer:
482.84
Step-by-step explanation:
\(A = 2 ( 1 +\sqrt{2} ) a^{2} = 2 multiply ( 1 +\sqrt{2} ) multiply 10^{2} = 482.84271\)
Hope it helps!!!Brainliest pls!!!
I am really sorry but just think that the "MULTIPLY" is when you just have to multiply the number and I can't change it.
Evaluate 7 Σ n=1 2(-2)^n-1.
Answers
Answer:
86
Step-by-step explanation:
I assume the question is \( \sum_{n=1}^{7} 2(-2)^{n-1} \)
7: 2(-2)^6 = 128
6: 2(-2)^5 = -64
5: 2(-2)^4 = 32
4: 2(-2)^3 = -16
3: 2(-2)^2 = 8
2: 2(-2)^1 = -4
1: 2(-2)^0 = 2
128 - 64 + 32 - 16 + 8 - 4 + 2 = 86
The school's Environmental Science Club has $500 of funds. Each time they go on a field trip, it costs
them $80. Write an algebraic expression that represents the money the club has after going on field
trips. Use the Math equation tool va to answer the question.
Answers
Given:
Total fund = $500
cost of each trip = $80
To find:
The an algebraic expression that represents the money the club has after going on field trips.
Solution:
Let x be the number of field trips.
Cost of 1 field trip = $80
Cost of x field trip = $80x
We have, Total fund = $500.
So, the money the club has after going on field trips is
\(\text{Remaining money}=500-80x\)
Therefore, the money the club has after going on field trips is $(500-80x).
Please help fast! 25 points and brainliest!! Let f(x) = 36x5 − 44x4 − 28x3 and g(x) = 4x2. Find f of x over g of x
Answers
Answer:
fx/gx=10
Step-by-step explanation:
fx= (36x5)-(44x4)-(28x3)
fx=80
gx= 4x2
gx=8
To work out fx/gx:
fx/gx=80/8
fx/gx=10
PLEASE HELP ME, ILL GIVE BRAINLIEST AND 70 POINTS

Answers
Answer:
√65 feet
Step-by-step explanation:
Using the pathagoryoes theroem (the equation in your picture) we have
4²+7²=c²
simplify to
16+49=c²
65=c²
√65=c
Part B
Assume the statement is true for n=k. Prove that it must be true for n=k+1, therefore proving it true for all natural
numbers, n.
Hint: Since the total number of dots increases by n each time, prove that d (k) + (k+1)=d(k+1).
BIUX¹ X₂ 15px
AVE
V
Answers
We have proved below that d( k+1) is only true when d(k) is true , also d(1) should also be true using Mathematical Induction.
Mathematical Induction : For each and every natural number n, mathematical induction is a method of demonstrating a statement, theorem, or formula that is presumed to be true.
It is given that the statement is true for n = k
Explanation:
According to the principle of Mathematical Induction,
Let d(n) be a statement involving Natural Number n such that
d(1) is true
d(m) is true
d(m+1) is true
So , the statement d(n) is true for all the n natural numbers.
According to the second principle of Mathematical Induction
Let d(n) be a statement involving Natural number n such that
d(1) is true
d(m) is true when d(n) is true for all n where 1 ≤ n ≤m .
Then the statement d(n) is true for all the values of n ( natural number)
Therefore , we have proved below that d( k+1) is only true when d(k) is true , also d(1) should also be true using Mathematical Induction.
To know more about Mathematical Induction visit: brainly.com/question/1333684
#SPJ9
A study on students drinking habits wants to determine the true average number of alcoholic drinks all UF "greek" students have in a one week! period. We know from preliminary studies that the standard deviation is around 6.3. How many students should be sampled to be within 0.5 drink! of population mean with 95% probability? 609 *305 304 610
Answers
Number of students should be sampled to be within 0.5 drink of population mean with 95% probability is 617 students.
To determine the sample size required to estimate the population mean with a given level of precision, we can use the formula for the margin of error
Margin of error = Z × (standard deviation / sqrt(sample size))
where Z is the critical value of the standard normal distribution corresponding to the desired level of confidence. For a 95% confidence level, Z is 1.96.
We want the margin of error to be no more than 0.5 drinks, so we can set up the equation
0.5 = 1.96 × (6.3 / sqrt(sample size))
Solving for the sample size, we get
sqrt(sample size) = 1.96 × 6.3 / 0.5
sqrt(sample size) = 24.82
sample size = (24.82)^2
sample size = 617
Learn more about margin of error here
brainly.com/question/10501147
#SPJ4
differentiate y= (x²-x)^9(√5x²+4x)
Answers
The given expression is
= (x²-x)^9(√5x²+4x)
We would differentiate it by applying the product rule. It is expressed as
(fg)' = f'g + fg'
Let f = (x²-x)^9
Let g = (√5x²+4x)
f' = 9(2x - 1)(x²-x)^8
g = (√5x²+4x) = (5x²+4x)^1/2
g' = 1/2(10x + 4)(√5x²+4x)^-1/2
g' = (10x + 4)/2(√5x²+4x)
g' = (5x + 2)/(√5x²+4x)
By applying the rule, it becomes
9(2x - 1)(x²-x)^8 * (√5x²+4x) + (x²-x)^9 * (5x + 2)/(√5x²+4x)
By simplifying,
\(y^{\prime}\text{ = }\frac{5x(x^2-x)^9+\text{ 2\lparen x}^2-x)^9+\text{ 90x}^3(x^2-x)^8+27x^2(x^2-x)^8-36x(x^2-x)^8}{\sqrt{5x^2\text{ + 4x}}}\)Solve for .x.
-9 + 2x + x-3
Answers
Answer:
I belive the answer is 3x - 12
An X-brace on a rectangular barn door is both decorative and functional. It helps to prevent the door from warping over time. If ST= 3 (13/16) feet, PS = 7 feet, and m∠PTQ = 67 , find the measure.
m∠TQR
Answers
The measure of angle TQR of the X brace on a rectangular barn door is approximately 40.577°.
To find the measure of angle ∠TQR, we can use the given information and apply the properties of angles in a triangle.
Since we know the lengths of two sides of the triangle, ST and PS, we can use the Law of Cosines to find the length of the third side, PT.
The Law of Cosines states:
c² = a² + b² - 2ab * cos(C)
In this case, we have:
PT² = ST² + PS² - 2(ST)(PS) * cos(m∠PTQ)
Substituting the given values:
PT² = (3 (13/16) ft)² + (7 ft)² - 2(3 (13/16) ft)(7 ft) * cos(67°)
Calculating this expression, we find:
PT ≈ 9.679 ft (rounded to three decimal places)
Now that we know the lengths of all three sides of the triangle (ST, PS, PT), we can use the Law of Cosines again to find the measure of angle ∠TQR.
The Law of Cosines states:
cos(C) = (a² + b² - c²) / (2ab)
In this case, we have:
cos(m∠TQR) = (ST² + PT² - PS²) / (2(ST)(PT))
Substituting the given values:
cos(m∠TQR) = [(3 (13/16) ft)² + (9.679 ft)² - (7 ft)²] / [2(3 (13/16) ft)(9.679 ft)]
Calculating this expression, we find:
cos(m∠TQR) ≈ 0.774 (rounded to three decimal places)
Finally, to find the measure of angle ∠TQR, we can take the inverse cosine (arccos) of the calculated cosine value:
m∠TQR ≈ arc cos(0.774) ≈ 40.577° (rounded to three decimal places)
Therefore, the measure of angle ∠TQR is approximately 40.577°.
To know more about angle refer here:
https://brainly.com/question/31186705
#SPJ11
Ayuda es para mañana El estudiante 1 y el estudiante 2 están a 53 metros, uno del otro. El estudiante 1, desde su posición, ve una caja fuerte, e inmediatamente mide el ángulo que el mismo forma con el estudiante 2, resultando de 37°. El estudiante 2, al advertirlo , mide enseguida el ángulo que forma la caja fuerte con el estudiante 1, resultando de 43°. ¿cual de los dos se halla más cerca de la caja fuerte?
A. El estudiante 2, ya que está aproximadamente a 32,29 metros.
B. El estudiante 1, ya que está aproximadamente a 32,29 metros.
C. El estudiante 2, ya que está aproximadamente a 37,28 metros.
D. El estudiante 1, ya que está aproximadamente a 37,28 metros.
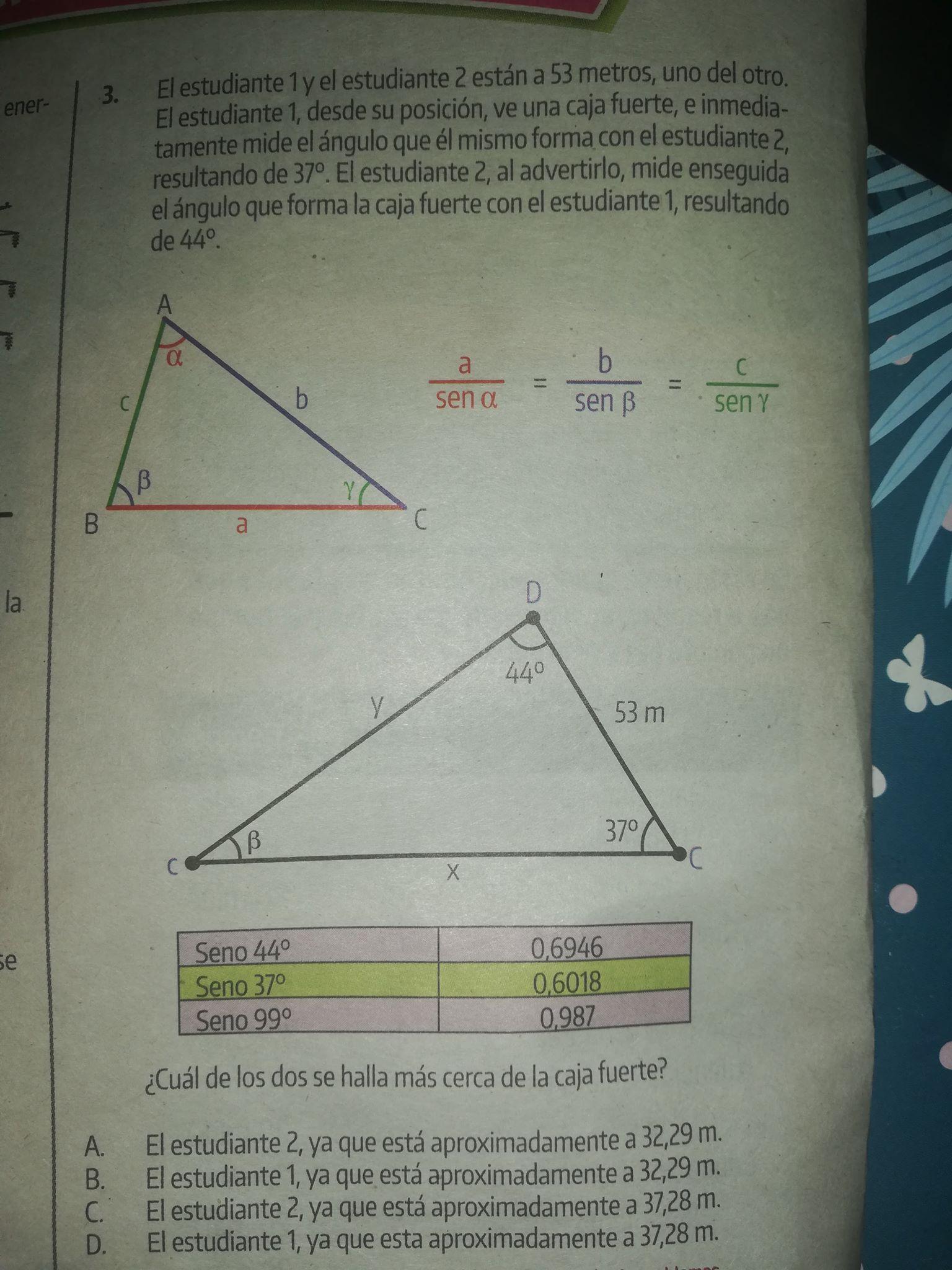
Answers
Answer:
La opción correcta es;
Estudiante 2, ya que está aproximadamente a 32,39 metros de distancia
Step-by-step explanation:
Los parámetros dados son;
La distancia entre los dos estudiantes = 53 metros
El ángulo medido entre la línea del Estudiante 1 a la caja fuerte y el Estudiante 1 y el Estudiante 2 = 37 °
El ángulo medido entre la línea del Estudiante 2 a la caja fuerte y el Estudiante 2 y el Estudiante 1 = 43 °
Dado que los dos estudiantes y la caja fuerte forman los vértices de un triángulo, tenemos;
Sea θ el ángulo del triángulo opuesto a la distancia entre los dos estudiantes
Por lo tanto;
θ + 43 ° + 37 ° = 180 ° (teorema de suma de ángulos)
θ = 180 ° - (43 ° + 37 °) = 100 °
Por regla del seno, tenemos;
a / (sin (A) = b / sin (B)
Por lo tanto;
53 / (sin (100 °)) = b / (sin (37 °)) = c / (sin (43 °))
Lo que da;
b = (sin (37 °)) × 53 / (sin (100 °)) = 32,39 metros
c = (sin (43 grados)) × 53 / (sin (100 grados)) = 36,7 metros
Por lo tanto, el Estudiante 2 está más cerca, ya que está aproximadamente a 32,39 metros de distancia.
the table defines a discrete probability distribution. find the expected value of the distribution. x 0 1 2 3 pr(x) 3/16 3/16 1/8 1/2
Answers
To find the expected value of a discrete probability distribution, we multiply each possible outcome by its probability and then sum the products. In this case, we have:
E(X) = 0(3/16) + 1(3/16) + 2(1/8) + 3(1/2)
= 0 + 3/16 + 1/4 + 3/2
= 1.5
Therefore, the expected value of this distribution is 1.5.
In probability theory, the expected value (also known as the mean or average) of a discrete probability distribution is a measure of the central tendency of the distribution. It represents the theoretical long-term average of the values taken by a random variable over an infinite number of trials.
To find the expected value of a discrete probability distribution, we multiply each possible value of the random variable by its corresponding probability and add up the products. In other words, if X is a discrete random variable with possible values x1, x2, ..., xn and corresponding probabilities p1, p2, ..., pn, then the expected value E(X) is:
E(X) = x1 * p1 + x2 * p2 + ... + xn * pn
For example, consider the discrete probability distribution given in the table:
x | 0 | 1 | 2 | 3
pr(x) | 3/16| 3/16| 1/8 | 1/2
To find the expected value of this distribution, we multiply each possible value of X by its corresponding probability and add up the products:
E(X) = 0*(3/16) + 1*(3/16) + 2*(1/8) + 3*(1/2) = 0 + 0.1875 + 0.25 + 1.5 = 1.9375
Therefore, the expected value of this distribution is 1.9375.
To learn more about discrete probability distribution refer below
https://brainly.com/question/9602705
#SPJ11
HELPPP PLEASE
Also I used line A as a place holder I don’t know if it’s right

Answers
Answer:
Line A is the right answer.
Answer:
a is right linear means straight line
Step-by-step explanation:
if y1 and y2 are continuous random variables with joint density function f (y1, y2) = ky1e−y2 , 0 ≤ y1 ≤ 1, y2 > 0, find (a) k, (b) fy1 (y1) and (c) f (y2 | y1 < 1/2).
Answers
If y1 and y2 are continuous random variables with joint density function f (y1, y2) = ky1e−y2 , 0 ≤ y1 ≤ 1, y2 > 0 then,
a) k = 1 - e^(-1) ≈ 0.632,
b) fy1(y1) = ∫f(y1, y2)dy2 = ky1∫e^(-y2)dy2 = ky1(-e^(-y2))|y2=0 to y2=∞ = k*y1,
c) f(y2 | y1 < 1/2) = f(y1,y2)/fy1(y1) = e^(-y2)/(1 - e^(-1))*y1, for 0 ≤ y1 ≤ 1/2 and y2 > 0.
(a) To find k, we must integrate the joint density function over the entire range of y1 and y2, and set the result equal to 1, since the density function must integrate to 1 over its domain:
∫∫ f(y1,y2) dy1 dy2 = 1
∫0∞ ∫0¹ f(y1,y2) dy1 dy2 = 1
∫0∞ (k y1 e^-y2) dy2 ∫0¹ dy1 = 1
k ∫0∞ (y1 e^-y2) dy2 ∫0¹ dy1 = 1
k ∫0¹ y1 dy1 ∫0∞ e^-y2 dy2 = 1
k(1/2)(1) = 1
k = 2
Therefore, the joint density function is f(y1,y2) = 2y1e^-y2, 0 ≤ y1 ≤ 1, y2 > 0.
(b) To find fy1(y1), we must integrate the joint density function over all possible values of y2:
fy1(y1) = ∫0∞ f(y1,y2) dy2
fy1(y1) = 2y1 ∫0∞ e^-y2 dy2
fy1(y1) = 2y1(1) = 2y1
Therefore, fy1(y1) = 2y1, 0 ≤ y1 ≤ 1.
(c) To find f(y2 | y1 < 1/2), we need to use Bayes' rule:
f(y2 | y1 < 1/2) = f(y1 < 1/2 | y2) f(y2) / f(y1 < 1/2)
We know that f(y2) = 2y1e^-y2 and f(y1 < 1/2) = ∫0^(1/2) 2y1e^-y2 dy1.
First, we need to find f(y1 < 1/2 | y2):
f(y1 < 1/2 | y2) = f(y1 < 1/2, y2) / f(y2)
f(y1 < 1/2, y2) = ∫0^(1/2) ∫0^y2 2y1e^-y2 dy1 dy2
f(y2) = ∫0∞ ∫0^1 2y1e^-y2 dy1 dy2
Using these equations, we can find:
f(y1 < 1/2 | y2) = ∫0^(1/2) ∫0^y2 2y1e^-y2 dy1 dy2 / ∫0∞ ∫0^1 2y1e^-y2 dy1 dy2
f(y1 < 1/2 | y2) = 1 - e^(-y2/2)
f(y2) = 2y1e^-y2
f(y1 < 1/2) = ∫0^(1/2) 2y1e^-y2 dy1 = [2(1-e^(-y2/2))] / y2
Substituting these expressions back into Bayes' rule, we get:
f(y2 | y1 < 1/2) = (1 - e^(-y2/2)) * y1e^-y2 / (1-e^(-y2/2))
Simplifying this expression, we get:
f(y2 | y1 < 1/2) = y1 * e^(-y2/2), 0 < y2 < ∞
Therefore, the conditional density of y2 given that y1 < 1/2 is f(y2 | y1 < 1/2) = y1 * e^(-y2/2), 0 < y2 < ∞.
Learn more about continuous random variables:
https://brainly.com/question/12970235
#SPJ11
TEST What is the locus of points three inches above the top of a table that measures four feet by eight feet? Construct the locus of points in a plane that are equidistant from the sides of A and at a distance d from point P. Label the locus points X. Cons 520 20
Answers
The locus of points three inches above the top of a table that measures four feet by eight feet is a rectangle parallel to the table's surface and located three inches above it. To construct the locus of points in a plane that are equidistant from the sides of a triangle A and at a distance d from point P, we can draw perpendicular bisectors from the sides of A and locate the points where these bisectors intersect. These points will form the locus of points equidistant from the sides of A and at a distance d from point P, labeled as X.
1. The locus of points three inches above the top of a table that measures four feet by eight feet is a rectangle with dimensions four feet by eight feet, parallel to the table's surface and located three inches above it.
2. To construct the locus of points in a plane that are equidistant from the sides of triangle A and at a distance d from point P, we can draw perpendicular bisectors from the sides of A.
3. The perpendicular bisectors will intersect at points that are equidistant from the sides of A and at a distance d from point P. These points form the locus of points and are labeled as X.
4. The locus of points X can be visualized as a set of points forming a shape in the plane.
To know more about bisectors intersect here: brainly.com/question/29548646
#SPJ11
