Given the area of a circle to be 10 inches^2 what is the radius and the diameter the circumference
Answers
Answer:
Radius = 1.78 inches
Diameter = 3.56 inches
Circumference = 11.18 inches
Step-by-step explanation:
Area of circle = 10 inches square
\(\pi r^2 = 10\\r^2 = \frac{10}{3.14}\\r^2 = 3.18\\\sqrt{r^2}=\sqrt{3.18}\\r=1.78\)
Radius = 1.78 inches
Diameter = 2r = 2(1.78) = 3.56 inches
Circumference = 2πr = 2*3.14*1.78 = 11.18 inches
Related Questions
13. Jessica has taken 8 quizzes. The mean of her scores is 92. Her first 6 scores are shown.
96, 90, 88, 92, 94, 90
If Jessica got the highest score possible on her seventh quiz, what score did she get on her
eighth quiz? What would be her median score Show your work and explain your reasoning.
Answers
Answer: Median= 91; 8th quiz score=86
Step-by-step explanation: The sum of the scores is 8×92=736. Subtract the 6 given scores and then a 100 for the seventh quiz to find the score she got on the 8th quiz, this is an 86. Now that you have all the scores, arrange them all in the least to greatest order and find the average of the middle two numbers (median), which is 91!
Find the area of the circle and the area of the sector round your answer to the nearest tenths

Answers
Area of the circle
The are of a circle is given by:
\(A(\text{circle) = }\pi\cdot r^2\)Where:
π = 3.14159
r = radius of the circle
In our problem we have:
r = 5
So, applying the formula of above we find that:
\(A(\text{circle) = }\pi\cdot5^2\cong78.5398\cong78.5\)Circle Area = 78.5 mi²
Area of the sector area of the circle
We can calculate the area of a sector of a circle using the following formula:
\(A(\text{sector) = }\pi\cdot r^2\cdot\frac{\theta}{360}\)Where:
θ = angle of the sector
In our problem we have:
θ = 60°
So, applying the formula of above we find that:
\(A(\text{sector) = }\pi\cdot5^2\cdot\frac{60}{360}\cong13.0899\cong13.1\)Sector Area = 13.1 mi²
Since the mode is the most frequently occurring data value, it
Select one:
a. is always larger than the mean
b. can never be larger than the mean
c. must have a value of at least two
d. is always larger than the median
e. None of these answers is correct.
Any answer without justification will be rejected automatically.
Answers
The correct answer is option (e): None of these answers is correct.
The statement "the mode is the most frequently occurring data value" is true. However, none of the options provided accurately describes the relationship between the mode and the mean.
The mode and the mean are different measures of central tendency and can have different values. There is no general rule or guarantee that the mode will always be larger or smaller than the mean. The relationship between the mode and the mean depends on the specific dataset and its distribution. Therefore, none of the provided options correctly describes the relationship between the mode and the mean.
Answer this question

Answers
The domain and range for the function shown in the graph above include the following:
D. D: [-∞, ∞]
R: [-10, ∞]
What is a domain?In Mathematics and Geometry, a domain refers to the set of all real numbers (x-values) for which a particular function (equation) is defined.
In Mathematics and Geometry, the horizontal portion of any graph is used to represent all domain values and they are both read and written from smaller to larger numerical values, which simply means from the left of any graph to the right.
By critically observing the graph shown in the image attached above, we can reasonably and logically deduce the following domain and range:
Domain = [-∞, ∞] or all real numbers.
Range = [-10, ∞] or y ≥ -10
Read more on domain here: brainly.com/question/9765637
#SPJ1
Which graph shows y=2⌊x⌋+1?

Answers
Find the product (x+2) (x+7) Why is the product also a polynomial?
Answers
The given product is, (x + 2) (x + 7).
We can expand the product as,
\((x+a)(x+b)=x^2+x(a+b)+ab\)Applying the expansion, we have,
\(\begin{gathered} (x+2)(x+7)=x^2+x(2+7)+(2\times7) \\ \text{ =x}^2+9x+14 \end{gathered}\)A polynomial is an expression consisting of variables (also called indeterminates) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables.
Since the resultant satisfies this condition, the resultant is also a polynomial.
Find the flaw with the following "proof" that every postage of 3 cents or more can be formed using just 3-cent and 4-cent stamps.Basis Step: We can form postage of 3 cents with a single 3-cent stamp, and we can form postage of 4 cents using a single 4-cent stamp.Inductive Step: Assume that we can form postage of j cents for all nonnegative integers j with j ≤ k using just 3-cent and 4-cent stamps. We can then form postage of k + 1 cents by replacing one 3-cent stamp with a 4-cent stamp or by replacing two 4-cent stamps by three 3-cent stamps.Which of these statements describes a flaw in the proof?
Answers
Answer:
The main flaw of this proof is that it did not take into consideration the fact a 4 cent postage must be made with a 4 cent stamp and a 3 cent postage must be made with a 3 cent stamp but only looked at allocating the stamps based on the total amount of postage
Step-by-step explanation:
From the question we are told that
The proof is
Every postage stamp of three cents or more can be formed using just 3 cent and 4 cent stamps.
Basic Step : We can form postage of 3 cents with a single 3 cent stamp and we can form postage of 4 cents using a single four cents tamp
Inductive Step: Assume that we can form postage of j cents for all non negative integers j with j <= k using just 3 cent and 4-cent stamps. We can then form postage of k+1 cents by replacing one 3 cent stamp with a 4-cent or two 4-cent stamps with three 3-cent stamps
FLAW IDENTIFICATION
Looking the inductive step, the statement ''by replacing one 3 cent stamp with a 4-cent or two 4-cent stamps with three 3-cent stamps '' means that it is possible to use a 3-cent stamp for postage that requires a 4 -cent stamp and this is not correct according the statement in the basic step
Generally the main flaw of this proof is that it did not take into consideration the fact a 4 cent postage must be made with a 4 cent stamp and a 3 cent postage must be made with a 3 cent stamp but only looked at allocating the stamps based on the total amount of postage
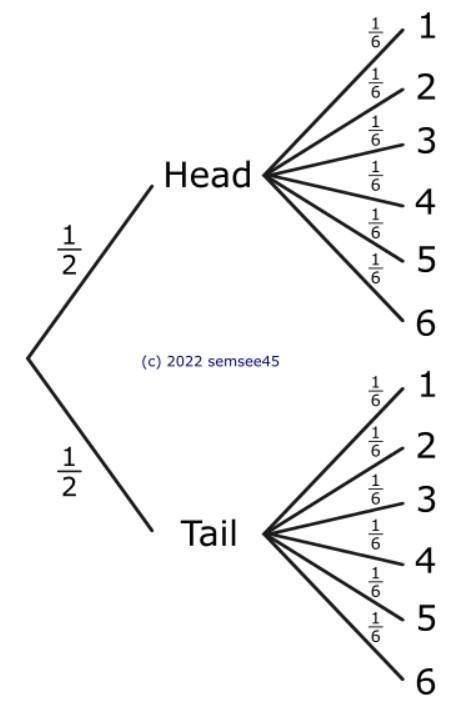
You flip a coin and then roll a 6-sided number cube (a die).
a. When finding the probability, does it matter whether you roll the die or flip the coin first?
b. Is there more than one way to draw a tree diagram for this problem? If so, does that change the likelihood that any outcome will occur?
c. Draw the shape of the tree diagram that you would use.
d. How many outcomes are there? List them.
e. Find the probability of rolling an even number and getting heads.
Answers
Answer:
a) No, it does not matter whether you roll the die or flip the coin first, as these two events are independent of each other, which means they do not affect each other.
b) Yes.
Let event 1 be flipping a coin and event 2 be rolling a die.Let event 1 be rolling a die and event 2 be flipping a coin.The likelihood that any outcome will occur will not change, as the events are independent.
c) see attached
d) 12 outcomes (H = head, T = tail, numbers represent the value of the die)
H 1 T 1
H 2 T 2
H 3 T 3
H 4 T 4
H 5 T 5
H 6 T 6
e)
\(\sf Probability\:of\:an\:event\:occurring = \dfrac{Number\:of\:ways\:it\:can\:occur}{Total\:number\:of\:possible\:outcomes}\)
\(\implies \sf P(even)=\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}=\dfrac{3}{6}=\dfrac{1}{2}\)
\(\implies \sf P(head)=\dfrac{1}{2}\)
\(\implies \sf P(even)\:and\:P(head)=\dfrac{1}{2} \times \dfrac{1}{2}=\dfrac{1}{4}\)
The heights of the low tides for four days are -0.22 ft, 2.64 ft, -0.22 ft, and 2.64 ft. What is the mean height of the low tides? (I need to show work.)
Answers
The mean height of the low tides is 1.21 ft
The heights of the low tides for four days are -0.22 ft, 2.64 ft, -0.22 ft, and 2.64 ft
The mean of a sample is given by the formula =
summation of all observation / number of observation
mean = (x₁ + x₂ + x₃ + x₄)/ 4
mean = -0.22 + 2.64 - 0.22 + 2.64 / 4
mean = 4.48 / 4 = 1.21
Therefore, the mean height of the low tides is 1.21 ft
To learn more about the mean refer here
https://brainly.com/question/20118982
#SPJ9
50 Points! Multiple choice geometry question. Photo attached. Thank you!

Answers
The calculated scale factor from ABC to A'B'C is 1/3
Calculating the scale factor from ABC to DEF?From the question, we have the following parameters that can be used in our computation:
The triangles
From the triangles, we have the following parameters
A = (0, 3)
A' = (0, 1)
Using the above as a guide, we have the following:
Scale factor of the dilation = A'/A
So, we have
Scale factor of the dilation = (0, 1)/(0, 3)
Evaluate
Scale factor of the dilation = 1/3
Hence, the scale factor of the dilation is 1/3
Read more about scale factor at
brainly.com/question/29229124
#SPJ1
PLEASE ANSWER WITH EXPLANATION
Beth and Alana are playing
Soccer. They both kick a ball
with an initial speed of 40 feet
per second. Beth kicked the ball
at a 55° angle and Alana kicked
the ball a 38° angle. Which
girl's ball went further and
by how many feet?
A) Beth; 1.43 ft
B) Beth; 1.29 ft
C) Alana; 1.38 ft
D) Alana; 1.51 ft
E) Alana; 1.64 ft
Answers
Answer: Nicole Kicked the ball Father by 22 feet than Tyrell.
Which girl's ball traveled the furthest, and by how far?The force of gravity caused the soccer ball to return to the girl.
By means of gravity, a planet or other body pulls items toward its center.
It is, in ideal circumstances, abiding by Newton's third law of gravitation and force.
Each action has a corresponding and opposing reaction.
So, when a boy kicks a ball and it comes back, that signifies he is abiding by the law.
Nicole kicked the ball 57 feet
Tyrel kicked the ball 35 feet
Nicole Kicked the ball Father by = 22feet
This is gotten by subtracting the distance Nicole kicked from that of Tyrel
=57 feet - 35feet = 22feet
To learn more about kicked the ball refer
https://brainly.com/question/21434205
#SPJ1
The graph (in red) shows the speed (m/s) of a car for 36 seconds.
A triangle has been drawn underneath part of the curve to estimate the distance travelled
between 30 and 36 seconds.
By using an appropriate single trapezium under the first part of the graph, estimate the total
distance travelled by the car in those 36 seconds.
30 T Speed (m/s)
25
20
15
10
5
O
0 5
10
15
20
25
Tirhe (seconds)
30
35
40
4
C Get help
5 -
-Area under a
Template.pdf
Area under a
Template.pdf
Report a mista
Quit assessme
On-screen key

Answers
To estimate the total distance traveled by the car in those 36 seconds, we can use the trapezium rule to approximate the area under the curve.
From the graph, we can see that the car's speed is constant between 0 and 30 seconds, and then it starts to decrease. Therefore, we can use a single trapezium to estimate the area under the curve for the first part.
The base of the trapezium is 30 seconds, and the height is the average of the speeds at 0 and 30 seconds. Let's denote the speed at 0 seconds as v0 and the speed at 30 seconds as v30.
The distance traveled in the first part can be estimated as:
Distance = 30 * (v0 + v30) / 2
To get a more accurate estimate, we need the specific values of v0 and v30 from the graph. Please provide the corresponding speed values for 0 and 30 seconds, and I can help you calculate the estimated distance.
Write a polynomial function f of least degree that has rational coefficients, a
leading coefficient of 1, and zeros 3 and 3 – i
Answers
Answer:
f(x) = x³ -9x² +28x -30
Step-by-step explanation:
You want a monic polynomial f of least degree with zeros 3 and 3-i.
FactorsFor zero x=a, the polynomial has a factor (x -a). Complex zeros come in conjugate pairs, so another one is 3+i. This means the factored form is ...
f(x) = (x -3)(x -3 +i)(x -3 -i)
f(x) = (x -3)(x² -6x +9 +1) . . . . . combine the two right factors
f(x) = x³ -9x² +28x -30
__
Additional comment
When multiplying polynomials mentally, it can be useful to consider the coefficients of the product terms in order of decreasing powers:
f(x) = (1)x³ +(-3 -6)x² +(10 +(-3)(-6))x +(-3)(10)
PLEASE HELP FAST!!
Determine the number of solutions to the system of linear equations shown on the graph.
A: No solution
B: Infinitely many solutions
C: One solution at (-3,2)
D:One solution at (2,-3)

Answers
Answer:
the answer is D
both lines intersect at (2, -3)
hope this helps <3
What is the solution to the following system of equations? (1 point) x − 3y = 6 2x + 2y = 4
Answers
Answer:
x = 3
y = -1
Step-by-step explanation:
Solving system of equations:Method: substitution
x - 3y = 6 --------------(I)
x = 6 + 3y -------------(II)
2x + 2y = 4 ----------(III)
Substitute x = 6 +3y in equation (II),
2*(6+3y) + 2y = 4
Use distributive property to open the parenthesis,
2*6 + 2*3y + 2y = 4
12 + 6y + 2y = 4
Combine like terms.
12 + 8y = 4
Subtract 12 from both sides,
8y = 4 - 12
8y = -8
Divide both sides by 8,
y = -8÷ 8
\(\boxed{\bf y = (-1)}\\\)
Substitute y = -1 in equation (II) and find the value of x.
x = 6 + 3*(-1)
= 6 - 3
\(\sf \boxed{\bf x = 3}\)
Answer:
(3, - 1 )
Step-by-step explanation:
x - 3y = 6 ( add 3y to both sides )
x = 3y + 6 → (1)
2x + 2y = 4 → (2)
substitute x = 3y + 6 into (2)
2(3y + 6) + 2y = 4
6y + 12 + 2y = 4
8y + 12 = 4 ( subtract 12 from both sides )
8y = - 8 ( divide both sides by 8 )
y = - 1
substitute y = - 1 into (1)
x = 3(- 1) + 6 = - 3 + 6 = 3
solution is (3, - 1 )
What is wrong with the following proof that for every integer n, there is an integer k such that n < k < n + 2? Suppose n is an arbitrary integer. Then k exists such that k = n + 1, proving n < n + 1 < n + 2. Nothing. 'Then k exists such that k = n + 1" is abuse of existential language. Given the n, the existence of the number n+1 is not in question. It makes no sense to draw a conclusion from the definition of k that does not reference k. The inequality n < n + 1 < n + 2 is true for all n, prior to any choice for k. the -ing form "proving" is grammatically wrong. We do not use the phrase "exists., such that" to make a direct definition. To define k as n + 1, we say "let k = n + 1", "pick k = n + 1" or "select k = n + 1". It works the same way as for constants. To assign the value 3 to k, we say "let k = 3". We do not say "k exists such that k = 3".
Answers
In the given proof, the phrase " There exists k = n+1 " is not a general practice to write.
option (d) is correct [ans]
What is an Integer?An integer is a whole number that can be positive, negative, or zero, and does not include any fractional or decimal parts.
Integers are part of the set of numbers called the integers, which includes all positive numbers, negative numbers, and zero.
We write " Let k = n+1 or assume n = k+1".
And then, we say that, it is obvious that
n < k = n+1 < n+2 for any integer n.
Hence, option (d) is correct [ans]
Read more about integers here:
https://brainly.com/question/929808
#SPJ1
The independent variable is represented by the symbol(s)
1. Y
2. xy
3. Both A and B
4. X
5. None of the above
Answers
Answer:
4
Step-by-step explanation:
because variable is independent
if a=1 b =2and c= -3 find the value of a2b2c-2
Answers
Hello !
you made a typo with the c^-2 because otherwise it does not make a round result
\(a^{2} *b^{2} *c^{2} \\\\= 1^{2} *2^{2}* (-3)^{2} \\\\= 1*4*9\\\\\boxed{= 36}\)
if and which expression could be used to verify gx is the inverse of fx
Answers
The expression could be used to verify g(x) is the inverse of the f(x) is (1/5)(5x - 25) +5
The function
f(x) = 5x - 25
g(x) = 1/5x + 5
The function is defined as the mathematical statement that shows the relationship between two variables. If one variable is independent variable other variable will be dependent variable.
An inverse function is defined as that returns the original value for which a function has given the output.
f(x) = 5x - 25
g(x) = 1/5x + 5
Then the value of g(f(x)= (1/5)(5x - 25) +5
Therefore, the inverse of the function = (1/5)(5x - 25) +5
I have answered the question in general, as the given question is incomplete
The complete question is:
If f(x)=5x-25 and g(x)=1/5x+5, which expression could be used to verify g(x) is the inverse of f(x)?
a) 1/5(1/5x)+5
b) 1/5(5x-25)+5
c) (1/5x+5)
d) 5(1/5x+5)+5
Learn more about inverse function here
brainly.com/question/2541698
#SPJ4
Solve for x.
−5x−8>22
Enter your answer in the boxes to correctly state the solution.
Answers
Answer:
x < -6
Step-by-step explanation:
-5x - 8 > 22
Add 8 to both sides: -5x > 30
Divide both sides by 5: -x > 6
Divide both sides by -1 (reverse sign): x < -6
Answer:
x < -6
Step-by-step explanation:
First we want to move all terms not containing x to the right side
-5x > 22 + 8
-5x > 30
Then we want to divide
-5x/5 < 30/-5
30/-5
x < - 6
Which choice shows (5 + 9) + 10 correctly rewritten using the associative property
and then correctly simplified?
O 10 + (5 + 9) = 10 + 14 = 24
O 5+ (9 + 10) = 5 + 19 = 24
O 10 + (9+5) = 10 + 14 = 24
O 5+ (91+0) = 5 +91 = 96
Question ID: 116111
Submit
Copyright 2023 The MOC
Answers
The correct option for the expression (5 + 9) + 10 showing the associative property is 5+ (9 + 10) = 5 + 19 = 24
What is the associative property?The associative property of addition states that the sum of three or more numbers remains the same regardless of how the numbers are grouped.
Given that, an expression, (5 + 9) + 10
According to associative property of addition, (a+b)+c = a+(b+c)
Therefore,
(5 + 9) + 10 = 5+(9+10)
= 5+19
= 24
Hence, the correct option for the expression (5 + 9) + 10 showing the associative property is 5+ (9 + 10) = 5 + 19 = 24
Learn more about associative property, click;
https://brainly.com/question/30111262
#SPJ1
Which graph best represents the function f(x) = 10 ?

Answers
See the attached graph.

If f(x)= - 4x-4, g(x)= 4x² + 4x + 2, and h(x)= 3x2 – 3, find f(3).
f(3) =
(Simplify your answer.)
Answers
Answer:
\(f(3) = -16\)
Step-by-step explanation:
Given
\(f(x)= - 4x-4\)
\(g(x)= 4x^2 + 4x + 2\)
\(h(x)= 3x^2 - 3\)
Required
\(f(3)\)
We have:
\(f(x)= - 4x-4\)
Substitute \(x = 3\)
\(f(3) = -4 * 3 - 4\)
\(f(3) = -12 - 4\)
\(f(3) = -16\)
Hence:
\(f(3) = -16\)
$13,000 is deposited into a savings account with an annual interest rate of 3% compounded continuously. How much will be in the account after 5 years?
Round to the nearest cent.
$15,106.00
$15,103.85
$43,714.05
$66,979.54
Answers
Answer:
15,103.05
Step-by-step explanation:
Total amount in the saving account after 5 years in which the annual interest, compounded continuously, is $15,103.85.
What is compound interest?Compound interest is the amount charged on the principal amount and the accumulated interest with a fixed rate of interest for a time period.
The formula for the final amount with the compound interest formula can be given as,
\(A=P\times\left(1+\dfrac{r}{100n}\right)^{nt}\\\)
Here, A is the final amount (principal plus interest amount) on the principal amount P of with the rate r of in the time period of t.
$13,000 is deposited into a savings account with an annual interest rate of 3% compounded continuously.
The amount in account after 5 years can be calculated with the above formula as,
\(A=13000\times\left(1+\dfrac{3}{12\times100}\right)^{12\times5}\\A=15101.02\)
The total amount in the saving account after 5 years in which the annual interest, compounded continuously, is $15,103..85.
Learn more about the compound interest here;
https://brainly.com/question/24274034
Write fraction underneath the seashell

Answers
The solution is given below.
What is fraction?A fraction represents a part of a whole or, more generally, any number of equal parts. Fractions represent the parts of a whole or collection of objects. A fraction has two parts. The number on the top of the line is called the numerator. It tells how many equal parts of the whole or collection are taken. The number below the line is called the denominator.
here, we have,
from the given diagram we get,
1. fraction underneath the seashell is 1/3
2. fraction underneath the seashell is 1/4
3. fraction underneath the seashell is 1/2
4. fraction underneath the seashell is 1/4
To learn more on fraction click:
brainly.com/question/10354322
#SPJ9
For which equations is x = 9 a possible solution? Check all that apply.
Answers
The equation is true when x = 9,x = 9 is a solution to this equation.
To determine which equations have x = 9 as a possible solution, we need to check each equation individually. Here are the equations to consider:
3x - 18 = 15
Substituting x = 9, we have:
3(9) - 18 = 15
27 - 18 = 15
9 = 15
The equation is not true when x = 9. Therefore, x = 9 is not a solution to this equation.
2(x + 4) = 26
Substituting x = 9, we have:
2(9 + 4) = 26
2(13) = 26
26 = 26
The equation is true when x = 9. Therefore, x = 9 is a solution to this equation.
5x + 3 = 2x + 30
Substituting x = 9, we have:
5(9) + 3 = 2(9) + 30
45 + 3 = 18 + 30
48 = 48
The equation is true when x = 9
Based on the analysis, x = 9 is a possible solution for equations 2 and 3.
for more questions on equation
https://brainly.com/question/29174899
#SPJ8
7. From the observation deck of a skyscraper, Matthew
measures a 45° angle of depression to a ship in the harbor
below. If the observation deck is 1053 feet high, what is
the horizontal distance from the base of the skyscraper out
to the ship? Round your answer to the nearest tenth of a
foot if necessary.
Answers
The horizontal distance from the base of the skyscraper out to the ship would be 1053 feet.
What are the trigonometric ratios?Trigonometric ratios for a right-angled triangle are from the perspective of a particular non-right angle.
In a right-angled triangle, two such angles are there which are not right angled(not of 90 degrees).
The slanted side is called the hypotenuse.
Let d the horizontal distance from the base of the skyscraper out to the ship. Since the angle of depression is 45°, hence:
\(\text{Angle} = 90 - 45 = 45^o\)
Using trigonometric ratio:
\(tan(45) = \dfrac{d}{1053}\)
\(d = 1053\ \text{feet}\)
The horizontal distance from the base of the skyscraper out to the ship would be 1053 feet.
Find out more on trigonometric ratio at:
https://brainly.com/question/24349828
100 Points! Geometry question. Identify the similar triangles. Then find each measure. Photo attached. Please show as much work as possible. Thank you!

Answers
The triangles ABC and DBE are similar by the SAS similarity theorem
The measure of the side lengths AC is 16 units
How to identify the similar triangles.From the question, we have the following parameters that can be used in our computation:
The triangles ABC and DBE
These triangles have the following measures
Two similar corresponding sidesTwo equal corresponding anglesThis means that the triangles are similar by the SAS similarity theorem
How to find each measureUsing the SAS similarity theorem, we have the following equation
(x + 1)/12 = (x + 5)/15
Cross multiply the equation
15x + 15 = 12x + 60
So, we have
3x = 45
Divide by 3
x = 15
This means that
x + 1 = 15 + 1 = 16
x + 5 = 15 + 5 = 20
Hence, the measure of the side lengths are 16 and 20 units
Read more about similar triangles at
https://brainly.com/question/14285697
#SPJ1
Describe how to solve 3-7n=27
Answers
Answer:
n = -24/7
Step-by-step explanation:
3 -7n = 27
-7n = 24 Subtract 3 from both sides
n = -24/7 Divided by -7 both sides
So, the answer is n = -24/7
Answer:
Below
Step-by-step explanation:
Subtract 3 from both sides of the equation THEN divide both sides of the equation by - 7
Wei wants to prove that the segment joining midpoints of two sides of a
triangle is parallel to the third side.
Select the appropriate rephrased statement for Wei's proof.

Answers
Now we know PR∥QX , according to construction with transversal line TX.
∠PTS=∠QXS (Alternate angle)
In △PTS and △QSX
∠PTS=∠QXS (Alternate angle)
∠PST=∠QSX(vertically opposite angles)
PS=SQ(S is mid point of PQ)
△PTS≅△QSX(AAS rule)
So, TP=QX(CPCT)
As we know, TP=TR (T is midpoint)
Hence, TR=QX
Now, in quadrilateral TSQR
TS∥QR
Hence proved.
Know more about triangle,
https://brainly.com/question/13677972
#SPJ1