given points F(3,1), G(5,2) H(2,4), and J(1,6)
Determine if segment FG and HJ are parallel, perpendicular, or neither.
A parallel
B perpendicular
C neither
Answers
The slopes of perpendicular lines are opposite reciprocals
The true statement is that segments FG and HJ are perpendicular
How to determine the relationship between the segmentsThe coordinates of the points are given as:
F = (3,1)
G = (5,2)
H = (2,4)
J = (1,6)
Start by calculating the slopes of FG and HJ using the following slope formula
\(m = \frac{y_2 -y_1}{x_2 -x_1}\)
So, we have:
\(FG = \frac{2 -1}{5 -3}\)
\(FG = \frac{1}{2}\)
Also, we have:
\(HJ = \frac{6 - 4}{1 - 2}\)
\(HJ = \frac{2}{-1}\)
\(HJ = -2\)
To determine the relationship, we make use of the following highlights
Parallel lines have the same slopeThe slopes of perpendicular lines are opposite reciprocalsFrom the computation above, we have:
The slopes of both lines are not equalThe slopes are opposite reciprocals i.e. 2 = -1(-1/2)Hence, segment FG and HJ are perpendicular
Read more about perpendicular lines at:
https://brainly.com/question/2531713
Related Questions
What is the value of x ?

Answers
Answer:
x = 3
Step-by-step explanation:
Given two secants drawn from an external point to the circle, then
The product of the external part and the whole of one secant is equal to the product of the external part and the whole of the other secant, that is
x(x + 21) = (x + 1)(x + 1 + 14)
x² + 21x = (x + 1)(x + 15) ← expand using FOIL
x² + 21x = x² + 16x + 15 ( subtract x² + 16x from both sides )
5x = 15 ( divide both sides by 5 )
x = 3
Please help !!
Consider the line y = -2-4x.
What is the slope of a line perpendicular to this line?
What is the slope of a line parallel to this line?
Slope of a perpendicular line:
Slope of a parallel line:

Answers
For the line y = -2-4x, the slope of a line parallel to this line is -4 and the slope of a line perpendicular to this line is 1/4.
What is slope?
A line's steepness and direction are measured by the line's slope. Without actually using a compass, determining the slope of lines in a coordinate plane can assist in forecasting whether the lines are parallel, perpendicular, or none at all.
The equation for the line is - y = -2 - 4x.
The slope of a line is represented by the coefficient of the x term. In this case, the slope of the line y = -2 - 4x is -4.
The slope of a line perpendicular to a given line is the negative reciprocal of the slope of the given line. The negative reciprocal of -4 is 1/4.
So, the slope of a line perpendicular to y = -2 - 4x is 1/4.
The slope of a line parallel to a given line is the same as the slope of the given line.
So the slope of a line parallel to y = -2 - 4x is -4.
Therefore, the parallel and perpendicular slope is -4 and 1/4 respectively.
To learn more about slope from the given link
https://brainly.com/question/16949303
#SPJ1
solve the equation below
for the indicated variable
1/3ab^2=6 (solve for a)
Answers
Answer:
a=18/b2
Step-by-step explanation:
The required equation for the indicated variable is a = 18/b² which is solved for a.
What is an equation?The equation is defined as mathematical statements that have a minimum of two terms containing variables or numbers that are equal.
What are Arithmetic operations?Arithmetic operations can also be specified by subtracting, dividing, and multiplying built-in functions. The operator that performs the arithmetic operation is called the arithmetic operator.
We have been given the equation for the indicated variable as
⇒ 1/3ab² = 6
Multiply by 3 both sides of the above equation,
⇒ ab² = 6×3
⇒ ab² = 18
Divide by b² into both sides of the equation, and we get
⇒ a = 18/b²
Therefore, the required equation for the indicated variable is a = 18/b².
Learn more about the equation here:
brainly.com/question/10413253
#SPJ2
if cos(2theta) = 10/19 adn pi/2<2theta
Answers
When cos(2θ) = 10/19 and π/2 < 2θ then a) The value of cos(θ) is -√(29/38). b) The value of sin(θ) is ±√(9/38). c) The value of tan(2θ) is (29/10)(±√(9/38)).
Given that cos(2θ) = 10/19 and π/2 < 2θ, we can find the values of cos(θ), sin(θ), and tan(2θ).
We know the double-angle identity for cosine, which states that cos(2θ) = 2\(cos^2\)(θ) - 1.
Substituting the given value cos(2θ) = 10/19 into the equation, we have 2\(cos^2\)(θ) - 1 = 10/19.
Simplifying this equation, we get 2\(cos^2\)(θ) = 29/19.
Dividing both sides by 2, we have \(cos^2\)(θ) = 29/38.
Taking the square root of both sides, we get cos(θ) = ±√(29/38).
Since π/2 < 2θ, we know that θ is in the second quadrant.
In the second quadrant, cosine is negative.
Therefore, we have cos(θ) = -√(29/38).
To find sin(θ), we can use the Pythagorean identity \(sin^2\)(θ) + \(cos^2\)(θ) = 1.
Substituting the value of cos(θ) = -√(29/38), we have \(sin^2\)(θ) + (-√(29/38))^2 = 1.
Simplifying, we get \(sin^2\)(θ) = 1 - 29/38
Evaluating the expression, we find \(sin^2\)(θ) = 9/38
Taking the square root of both sides, we have
sin(θ) = ±√(9/38)
Finally, to find tan(2θ), we can use the double-angle identity for tangent, which states that tan(2θ) = (2tan(θ))/(1 - \(tan^2\)(θ)).
Since tan(θ) is sin(θ)/cos(θ), we can substitute the values of sin(θ) and cos(θ) into the equation:
tan(2θ) = (2(sin(θ)/cos(θ)))/(1 - \((sin(\theta)/cos(\theta))^2\))
Substituting the values of sin(θ) and cos(θ), we have:
tan(2θ) = (2(±√(9/38)))/[1 - ((±√(9/38))/(√(29/38)))^2]
Simplifying further, we get:
tan(2θ) = (2(±√(9/38)))/[1 - (9/38)/(29/38)]
tan(2θ) = (2(±√(9/38)))/(1 - 9/29)
tan(2θ) = (2(±√(9/38)))/(20/29)
tan(2θ) = (29/10)(±√(9/38))
Therefore, tan(2θ) is equal to (29/10)(±√(9/38)).
Learn more about Pythagorean identity here:
https://brainly.com/question/95257
#SPJ11
The complete question is:
If cos(2θ) = 10/19 and π/2 < 2θ then find
a) cos(θ)
b) sin(θ)
c) tan(2θ)
A triangle has an area of 49.5cm2 If the base of the triangle is 9cm. What is the height of the triangle A = 1/2BH
Answers
Answer: 11
Step-by-step explanation:
49.5/9 = 5.5
5.5 x 2 =11
11x9=99
99/2=49.5
Layla owes
$8,500 on her credit card. The bank charges a monthly interest rate of 1.525%. If Layla wants to pay off her credit card using equal monthly payments over the next 12 months, what would the monthly payment be, to the nearest dollar?
Answers
By responding to the question, we can deduce that Layla must make a monthly payment of $\(742\) to the closest dollar in order to pay off her credit card debt over the course of the next \(12\) months.
What is equation?In mathematics, an equation is a claim that two expressions are equivalent. Two parts that are separated by the algebraic symbol (=) make up an equation. As an illustration, the claim "\(2x+3=9\)" makes the statement
Finding the value or values of the variable(s) necessary for the equation to be correct is the goal of equation solving.
Equations can have one or more components and be straightforward or complex, regular or nonlinear. The formula "\(x^{2} +2x-3 = 0\)" raises the variable x to the second degree. In many various branches of mathematics, including algebra, calculus, and geometry, lines are used.
\(pmt = pv*(r/1-(1+r)^{-n} ))\)
\(pmt= 8500*(0.1525/(1-(1+0.051525)^{-12} ))\\pmt= 8500*(0.1525/1- 0.82514))\\pmt= 8500*(0.1525/0.17486)\\pmt= 741.83\)
Therefore, the approximate monthly payment that Layla must make to clear off her credit card debt over the following \(12\) months is $\(742\).
Learn more about compound interest
https://brainly.com/question/14295570
#SPJ1
a rectangular storage container with a lid is to have a volume of 16 m3. the length of its base is twice the width. material for the base costs $8 per m2. material for the sides and lid costs $16 per m2. find the dimensions of the container which will minimize cost and the minimum cost.
Answers
The minimum cost of the container is $576, and the dimensions that minimize the cost are a width of 2 meters, length of 4 meters, and height of 2 meters.
To minimize the cost, we need to find the dimensions of the container that minimize the total cost, taking into account the cost of the base, sides, and lid.
Let's start by defining the dimensions of the rectangular container:
Let the width of the base be "w" meters.
The length of the base will be twice the width, so the length is "2w" meters.
The height of the container is "h" meters.
The volume of the container is given as 16 m³, so we can write the equation:
Volume = Length × Width × Height
16 = 2w × w × h
16 = 2w²h
w²h = 8 ----(Equation 1)
Now, let's find the cost of the base, sides, and lid.
Cost of the base:
The base is a rectangle with dimensions of length = 2w and width = w.
Area of the base = length × width
Area of the base = (2w) × w = 2w²
Cost of the base = Area of the base × Cost per m² = 2w² × $8 = 16w²
Cost of the sides and lid:
The container has two sides with dimensions of length = 2w and height = h.
The container has two sides with dimensions of width = w and height = h.
The container has a lid with dimensions of length = 2w and width = w.
Area of each side = length × height = 2w × h = 2wh
Area of each side = width × height = w × h
Area of the lid = length × width = 2w × w = 2w²
Total area of the sides and lid = 2(2wh) + 2(wh) + 2w² = 4wh + 2wh + 2w² = 6wh + 2w²
Cost of the sides and lid = Total area × Cost per m² = (6wh + 2w²) × $16 = 96wh + 32w²
Now, we need to express the cost in terms of one variable, either w or h, so we can find the minimum value. Since Equation 1 relates w, h, and the volume, we can express h in terms of w.
From Equation 1:
w²h = 8
h = 8/w²
Now, substitute h in the cost equation:
Cost = 16w² (cost of the base) + (96wh + 32w²) (cost of the sides and lid)
Cost = 16w² + 96w(8/w²) + 32w²
Cost = 16w² + 768/w + 32w²
Cost = 48w² + 768/w ----(Equation 2)
To find the minimum cost, we differentiate Equation 2 with respect to w and set it equal to zero:
d(Cost)/dw = 96w - 768/w² = 0
96w = 768/w²
w³ = 8
Taking the cube root of both sides:
w = 2
Substituting w = 2 back into Equation 1:
w²h = 8
(2)²h = 8
4h = 8
h = 2
Therefore, the dimensions of the container that minimize the cost are:
Width (w) = 2 meters
Length = 2w = 4 meters
Height (h) = 2 meters
The minimum cost can be found by substituting the values of w and h into Equation 2:
Cost = 48w² + 768/w
Cost = 48(2)² + 768/2
Cost = 48(4) + 384
Cost = 192 + 384
Cost = $576
So, the minimum cost of the container is $576, and the dimensions that minimize the cost are a width of 2 meters, length of 4 meters, and height of 2 meters.
To know more about minimum click here :
https://brainly.com/question/31429305
#SPJ4
example of two nonlinear functions that dont dominate each other
Answers
An example of two nonlinear functions that don't dominate each other is the sin function (f(x) = sin(x)) and the exponential function (g(x) = e^x).
For any given value of x, the sin function oscillates between -1 and 1, taking on both positive and negative values. It has a periodic nature and does not grow or decay exponentially as x increases or decreases.
On the other hand, the exponential function grows or decays exponentially as x increases or decreases. It is characterized by a constant positive growth rate. The exponential function increases rapidly when x is positive and approaches zero as x approaches negative infinity.
The key characteristic here is that the sine function oscillates while the exponential function grows or decays exponentially.
Due to their fundamentally different natures, neither function dominates the other over their entire domains.
Learn more about nonlinear functions from the given link:
https://brainly.com/question/17604622
what do the symbols p with hat on top, x with bar on top, and s represent? variables of interest sample statistics defined variables population parameters
Answers
The symbols p,x, and s represent sample statistics.
- p (pronounced "p-hat") is the sample proportion. It is used to estimate the population proportion. It is computed as the number of successes in the sample divided by the sample size.
-x (pronounced "x-bar") is the sample mean. It is used to estimate the population mean. It is computed as the sum of all the values in the sample divided by the sample size.
- s is the sample standard deviation. It is used to estimate the population standard deviation. It measures how spread out the data is in the sample. It is computed as the square root of the sum of the squared deviations from the sample mean divided by the sample size minus one.
These sample statistics are used to make inferences about the corresponding population parameters, which are denoted by Greek letters such as μ (mu) for the population mean and σ (sigma) for the population standard deviation.
To learn more about variables population parameters refer below:
https://brainly.com/question/16787328
#SPJ11
Side lengths: 24 in, 30 in, and 36 in
Answers
Volume of this is 25920 inches cubed
the national average.
If the national average for a gallon of gas is $2.59, how much
should you expect to pay for gas in Philadelphia versus
Cleveland?
A. $3.03 / $2.75
B. $1.95 / $2.59
C. $2.34 / $2.75
D. $2.75 / $3.24
Philadelphia Clevland
Overall 92 78
Food 106 106
Housing 56 27
Utilities 130 126
Transportation 117 106
Health 102 113
Answers
The correct answer is D. $2.75 / $3.24
To determine how much you should expect to pay for gas in Philadelphia versus Cleveland, we need to compare the transportation expenses in both cities. Based on the given data, the transportation expenses are as follows:
Philadelphia: $117
Cleveland: $106
To calculate the expected gas prices, we need to consider the transportation expenses relative to the national average. The formula to find the expected gas price is:
Expected Gas Price = National Average * (Transportation Expense / National Average)
National Average for gas = $2.59
For Philadelphia:
Expected Gas Price in Philadelphia = $2.59 * ($117 / 92) ≈ $3.30
For Cleveland:
Expected Gas Price in Cleveland = $2.59 * ($106 / 78) ≈ $3.51
Comparing the expected gas prices, we find that:
A. $3.03 / $2.75: This option does not match the expected gas prices in Philadelphia and Cleveland.
B. $1.95 / $2.59: This option does not match the expected gas prices in Philadelphia and Cleveland.
C. $2.34 / $2.75: This option does not match the expected gas prices in Philadelphia and Cleveland.
D. $2.75 / $3.24: This option matches the expected gas prices in Philadelphia and Cleveland.
Therefore, the correct answer is:
D. $2.75 / $3.24
for such more question on transportation expenses
https://brainly.com/question/11734493
#SPJ8
You can think of an array as a collection of variables contained within a single variable.a. Trueb. False
Answers
The correct answer is option A - True. An array is a data structure in programming that allows you to store a collection of values of the same data type in a single variable.
Each value is assigned an index number, starting from 0, which represents its position in the array. Arrays are useful in programming because they allow you to store and manipulate multiple values using a single variable. This can help simplify code and make it more efficient.
For example, if you wanted to store the grades of 10 students in a program, you could create an array of 10 elements and assign each grade to a specific index in the array. In addition to storing data, arrays can also be used to perform calculations and manipulate data.
For example, you could use a loop to iterate through an array and calculate the average of all the values stored in the array. Overall, arrays are a powerful tool in programming that can help you organize and manipulate data.
By thinking of an array as a collection of variables contained within a single variable, you can better understand how arrays work and how to use them effectively in your programs.
To know more about variable click here
brainly.com/question/2466865
#SPJ11
Please help me! :( 30 points
What are the x-values when y = 0 for this function?
x =
x =

Answers
Answer:
The x-values when y = 0 for this function are -2 and 3.
Answer:
Step-by-step explanation:
\(y=0\) when the graph cuts the x-axis.
So when \(y=0,\) \(x=-2\) and \(x=-9\).
Fill The Blank ?a function is a rule that assigns to each value of the_____
Answers
In essence, a function is a rule that assigns to each value of the input set (also known as the domain), a unique value of the output set (also known as the range).
A function is a fundamental mathematical concept that is used to describe the relationship between two sets of values.
To understand the idea of a function, imagine a machine that takes in an input and produces an output. The input values are the domain of the function, and the output values are the range. A function can be represented as an equation, a graph, or a table. For example, the equation f(x) = x + 3 represents a function that takes in an input value x and produces an output value that is 3 greater than the input value.
One of the key features of a function is that each input value must have a unique output value. This means that if you input the same value into the function twice, you should get the same output value both times. In mathematical terms, we say that a function is well-defined if it has a unique output value for each input value.
Functions are used in a wide range of mathematical applications, from algebra and calculus to statistics and data analysis. They provide a powerful tool for describing and analyzing relationships between different sets of values.
To know more about function here
https://brainly.com/question/28193995
#SPJ4
Use Theorem 9.11 to determine the convergence or divergence of the p-series. 1 8 2 27 3 64 4 125 5 O converges O diverges Need Help? Read t Lvlstchut LTalk to a Tutor Submit Answer save Progress Practice Another Version
Answers
Theorem 9.11 states that the p-series ∑_(n=1)^∞ 1/n converges if p > 1 and diverges if p ≤ 1.
In the given series, we can see that each term is of the form n^3, which can be written as (n^p)^3 where p=1/3.
Since p=1/3 is less than or equal to 1, we can conclude that the series diverges by applying Theorem 9.11.
Therefore, the given series diverges.
Using Theorem 9.11, we can determine the convergence or divergence of the given p-series. This theorem states that a p-series ∑_(n=1)^∞ 1/n^p converges if p > 1 and diverges if p ≤ 1.
If you meant to write the series as 1/8 + 2/27 + 3/64 + 4/125 + ... (with terms of the form n/n^3), then it is a p-series with p = 3 > 1. In this case, according to Theorem 9.11, the series converges.
learn more about theorems here: brainly.com/question/21571509
#SPJ11
Karl drove 40 miles in 50 minutes. Teresa drove 35 miles in 42 minutes. Who had a higher average speed?
Answers
The person that has the higher average speed is Teresa.
How to calculate average speed?The average speed is the total distance travelled by the object in a particular time interval.
Average speed measures the average rate of speed over the extent of a trip.
Therefore,
average speed = distance / time
Hence, Karl drove 40 miles in 50 minutes.
Therefore,
average speed of Karl = 40 / 50
average speed of Karl = 4 / 5 miles per minute
Teresa drove 35 miles in 42 minutes.
Therefore,
average speed of Teresa = 35 / 42
average speed of Teresa = 5 / 6 miles per minutes
Therefore, Teresa had the higher average speed.
learn more on average speed here: brainly.com/question/9802724
#SPJ1
Use the single variable regression model with house size as the independent variable to predict the selling price of a house that is 2,700 square feet.
Answers
We'll collect and analyze the data and then build the regression model and evaluate it in order to predict the selling price of a house that is 2,700 square feet using single variable regression model.
The single variable regression model assumes a linear relationship between the independent variable (house size) and the dependent variable (selling price). If the relationship is non-linear, a different regression model may be more appropriate.
Question: Use the single variable regression model with house size as the independent variable to predict the selling price of a house that is 2,700 square feet.
To predict the selling price of a house that is 2,700 square feet using the single variable regression model, we need to follow these steps:
1. Collect data: Obtain a dataset that includes information on house sizes and their corresponding selling prices. This dataset will be used to build the regression model.
2. Analyze the data: Examine the dataset to understand the relationship between house size and selling price. Plot a scatter plot to visualize the data points and determine if there is a linear relationship between the two variables.
3. Build the regression model: Fit a regression line to the data points using a statistical method like least squares regression. This line represents the relationship between house size (independent variable) and selling price (dependent variable).
4. Evaluate the model: Assess the quality of the regression model by calculating the coefficient of determination (R-squared value). This value measures how well the regression line fits the data. A higher R-squared value indicates a better fit.
5. Predict the selling price: Now that we have a regression model, we can use it to predict the selling price of a house with a given size. In this case, we want to predict the selling price of a house that is 2,700 square feet.
To predict the selling price of a house that is 2,700 square feet, we substitute the house size value (2,700) into the regression equation. The equation will give us the predicted selling price for a house of that size.
It's important to note that the accuracy of the prediction depends on the quality of the regression model. A higher R-squared value suggests a better prediction accuracy.
Remember, the single variable regression model assumes a linear relationship between the independent variable (house size) and the dependent variable (selling price). If the relationship is non-linear, a different regression model may be more appropriate.
Keep in mind that additional factors such as location, condition, and amenities can also influence the selling price of a house. Therefore, it's advisable to consider these factors in conjunction with the single variable regression model to make more accurate predictions.
To know more about single variable regression model refer here:
https://brainly.com/question/31735997
#SPJ11
adding and subtracting fractions with unlike denominators worksheets
Answers
First make the denominator equal by doing Least common multiple. One the denominator gets the same then add and subtract the fraction number.
What is Algebra?Algebra is the study of abstract symbols, while logic is the manipulation of all those ideas.
The acronym PEMDAS stands for Parenthesis, Exponent, Multiplication, Division, Addition, and Subtraction. This approach is used to answer the problem correctly and completely.
Adding and subtracting fractions with unlike denominators is calculated as,
First make the denominator equal by doing Least common multiple. One the denominator gets the same then add and subtract the fraction number.
More about the Algebra link is given below.
https://brainly.com/question/953809
#SPJ1
SOMEONE PLEASE HELP ME WITH MY MATH IT'S DUE TONIGHT AT MIDNIGHT AND I D K HOW TO DO THIS
NO LINKS OR I WILL REPORT YOU

Answers
When you’re finding a line perpendicular to a given equation, the slope will be the negative reciprocal: that is, if “m” is representing the current slope and “m’” represents the new slope, then m’ = -1/m. Therefore, the new slope will be -1/(-3) or simply 1/3. As for the point, we must substitute in the values with our current slope. If x0 is the x-intercept (what x equals when y=0), then we have y=(1/3)x + x0. If y=5 and x=8 as it is with the given point, we have 5=(1/3)(8) + x0. Solving this we get x0=(7/3)… then the equation of the first problem is y=(1/3)x + (7/3)
As for the second problem, the slope is the same (-3). Just have y=-3x+x0, and subbing in the point we have 5=-3(8)+x0. For this to be true, x0 must be 29 (found by solving the equation). Therefore the answer to the second problem is y=-3x+29.
Hope this helps!
Match the key features of the polynomial graph.

Answers
For the given graph local maximum (2.1,0.7), end behavior is positive infinity to negative infinity, local minimum (-2.7,-4.9), y interception (0,-1.5), and x interception will be at (2.1,0.7).
How to plot a graph?A graph is a diagram that shows the fluctuation of one variable in relation to one or more other variables.
In order to plot the graph, we need to find out y's values corresponding to x's value
After that, we need to substitute the values of x's and y's into the coordinate geometry.
Given the graph with 1 maximum and 1 minimum and 1 x and y-intercept.
A key feature of the polynomial graph ;
Local maximum (2.1,0.7),
End behavior is positive infinity to negative infinity,
Local minimum (-2.7,-4.9),
y interception (0,-1.5),
x interception (2.1,0.7).
Hence "For the given graph local maximum (2.1,0.7), end behavior is positive infinity to negative infinity, local minimum (-2.7,-4.9), y interception (0,-1.5), and x interception will be at (2.1,0.7)".
For more information about the graph of a function,
brainly.com/question/27757761
#SPJ1
The sum of an integer and 6 times the next consecutive odd integer is 61. Find the
value of the lesser integer.
Answers
If the sum of an integer and 6 times the next consecutive integer is 61, the the value of lesser integer is 7
Consider the first odd integer as x
Then the next consecutive odd integer = x+2
The 6 times the second integer= 6(x+2)
= 6x+12
Sum of an integer and 6 times the next consecutive odd integer is 61
Then the equation will be
x + 6x+12 = 61
Add the like terms in the equation
(1+6)x + 12 = 61
7x +12 = 61
Move 12 to the right hand side of the equation
7x = 61-12
7x = 49
x = 49/7
x = 7
The second number is
x+2 = 7+2
= 9
Hence, if the sum of an integer and 6 times the next consecutive integer is 61, the the value of lesser integer is 7
Learn more about equation here
brainly.com/question/28741857
#SPJ1
Help with right Awnser

Answers
Answer:
Solution given:
base[b]=8m
perpendicular [p]=3m
we have
area of triangle=\( \frac{p \times b}{2} \)
=\( \frac{3 \times 8}{2} \)=12m²
is your answer
Answer:
12m2
Step-by-step explanation:
Which expression is equivalent to log 20 + 2 log x - log y ? a) log(20x^2y) b) log(10x/y) c) log(20/x^2 y) d) log(20x^2 /y)

Answers
OPTION D
log(20x²/y)
is the correct answer
the answer is D!
Step-by-step explanation:
hope it helped!have a nice day!!!
"Please show all work and explain each step with theorems 2. (10) Find cos'(x) by using the definition of cosh(x) and solving for the inverse function. Write as a single expression (not piecewise)."
Answers
To find cos'(x), we can start by using the definition of the hyperbolic cosine function, cosh(x) = (e^x + e^(-x))/2.
Let y = cosh(x). Then we have:
y = (e^x + e^(-x))/2
2y = e^x + e^(-x)
Multiplying both sides by e^x, we get:
2ye^x = e^(2x) + 1
e^(2x) - 2ye^x + 1 = 0
This is a quadratic equation in e^x, so we can use the quadratic formula to solve for e^x:
e^x = (2y ± sqrt(4y^2 - 4))/2
e^x = y ± sqrt(y^2 - 1)
Since e^x is always positive, we choose the positive square root:
e^x = y + sqrt(y^2 - 1)
Taking the natural logarithm of both sides, we get:
x = ln(y + sqrt(y^2 - 1))
Now we can find cos'(x) by differentiating both sides with respect to x:
cos'(x) = d/dx ln(y + sqrt(y^2 - 1))
Using the chain rule, we have:
cos'(x) = 1/(y + sqrt(y^2 - 1)) * (d/dx y + sqrt(y^2 - 1))
Differentiating y = cosh(x) with respect to x, we get:
dy/dx = sinh(x) = (e^x - e^(-x))/2
Substituting back in y = cosh(x), we have:
dy/dx = sinh(ln(y + sqrt(y^2 - 1))) = (y + sqrt(y^2 - 1))/2
Now we can substitute both expressions back into cos'(x):
cos'(x) = 1/(y + sqrt(y^2 - 1)) * (y + sqrt(y^2 - 1))/2
Simplifying, we get:
cos'(x) = 1/2sqrt(y^2 - 1)
Substituting back in y = cosh(x), we get the final answer:
cos'(x) = 1/2sqrt(cosh^2(x) - 1)
Learn more about hyperbolic cosine function here:
https://brainly.com/question/15381243
#SPJ11
How many equal arcs can you divide the unit circle into using t-values that are multiples of pi/3?
Answers
The unit circle can be divided into 6 equal arcs using t-values that are multiples of π/3.
To determine the number of equal arcs that can be formed by dividing the unit circle using t-values that are multiples of π/3, we need to consider the angular measure between each division point.
A circle has a total angular measure of 360 degrees or 2π radians. Since we are using t-values that are multiples of π/3, each division point will have an angular measure of π/3.
To find the number of equal arcs, we divide the total angular measure of the circle (2π radians) by the angular measure between each division point (π/3 radians):
Number of equal arcs = (Total angular measure of the circle) / (Angular measure between each division point)
Number of equal arcs = (2π radians) / (π/3 radians)
Simplifying the expression, we get:
Number of equal arcs = (2π radians) * (3/π radians)
Number of equal arcs = 6
Therefore, the unit circle can be divided into 6 equal arcs using t-values that are multiples of π/3. Each arc will have an angular measure of π/3.
To learn more about unit circle, click here: brainly.com/question/29298870
#SPJ11
Use Cramer's rule to solve the system of equations: x−8y+z=4
−x+2y+z=2
x−y+2z=−1
9. Use Gaussian elimination to solve the system of equations: 3x−5y+2z=6
x+2y−z=1
−x+9y−4z=0
Answers
Solve the given system of equation using Cramer's rule:
x−8y+z=4
−x+2y+z=2
x−y+2z=−1
x = Dx/D, y = Dy/D, z = Dz/D .x−8y+z=4.....(1)−x+2y+z=2.....(2)x−y+2z=−1....(3)D = and Dx = 4 −8 1 2 2 1 −1 2 −1D = -28Dx = 4-8 -1(2) 2-1 2(-1) = 28+2+4+16 = 50Dy = -28Dy = 1-8 -1(2) -1+2 2(-1) = -28+2+8+16 = -2Dz = -28Dz = 1 4 2(2) 1 -1(1) = -28+16-16 = -28By Cramer's Rule,x = Dx/D = 50/-28 = -25/14y = Dy/D = -2/-28 = 1/14z = Dz/D = -28/-28 = 1
Hence, the solution of the given system of equations is x = -25/14, y = 1/14 and z = 1.
Solve the given system of equations using Gaussian elimination:
3x−5y+2z=6
x+2y−z=1
−x+9y−4z=0
Step 1: Using row operations, make the first column of the coefficient matrix zero below the diagonal. To eliminate the coefficient of x from the second and the third equations, multiply the first equation by -1 and add to the second and third equations.3x − 5y + 2z = 6..........(1)
x + 2y − z = 1............(2)−x + 9y − 4z = 0........
(3)Add (–1) × (1st equation) to (2nd equation), we get,x + 2y − z = 1............(2) − (–3y – 2z = –6)3y + z = 7..............(4)Add (1) × (1st equation) to (3rd equation), we get,−x + 9y − 4z = 0......(3) − (3y + 2z = –6)−x + 6y = 6............(5
)Step 2: Using row operations, make the second column of the coefficient matrix zero below the diagonal. To eliminate the coefficient of y from the third equation, multiply the fourth equation by -2 and add to the fifth equation.x + 2y − z = 1............(2)3y + z = 7..............
(4)−x + 6y = 6............(5)Add (–2) × (4th equation) to (5th equation),
we get,−x + 6y = 6............(5) − (–6y – 2z = –14)−x – 2z = –8..........(6)
Step 3: Using row operations, make the third column of the coefficient matrix zero below the diagonal. To eliminate the coefficient of z from the fifth equation, multiply the sixth equation by 2 and add to the fifth equation
.x + 2y − z = 1............(2)3y + z = 7..............(4)−x – 2z = –8..........(6)Add (2) × (6th equation) to (5th equation), we get,−x + 6y − 4z = 0....(7)Add (1) × (4th equation) to (6th equation), we get,−x – 2z = –8..........(6) + (3z = 3)−x + z = –5.............(8)Therefore, the system of equations is now in the form of a triangular matrix.3x − 5y + 2z = 6.........(1)3y + z = 7................(4)−x + z = –5...............(8)
We can solve the third equation to get z = 4.Substituting the value of z in equation (4), we get, 3y + 4 = 7, y = 1Substituting the values of y and z in equation (1), we get, 3x – 5(1) + 2(4) = 6, 3x = 9, x = 3Therefore, the solution of the given system of equations is x = 3, y = 1 and z = 4.
To know more about equation,visit:
https://brainly.com/question/29538993
#SPJ11
QN is tangent to circle O at point I. IA is the circle's diameter. Find m/QIA.
N
€
E
E
C
3
R
3
C
Help I need help
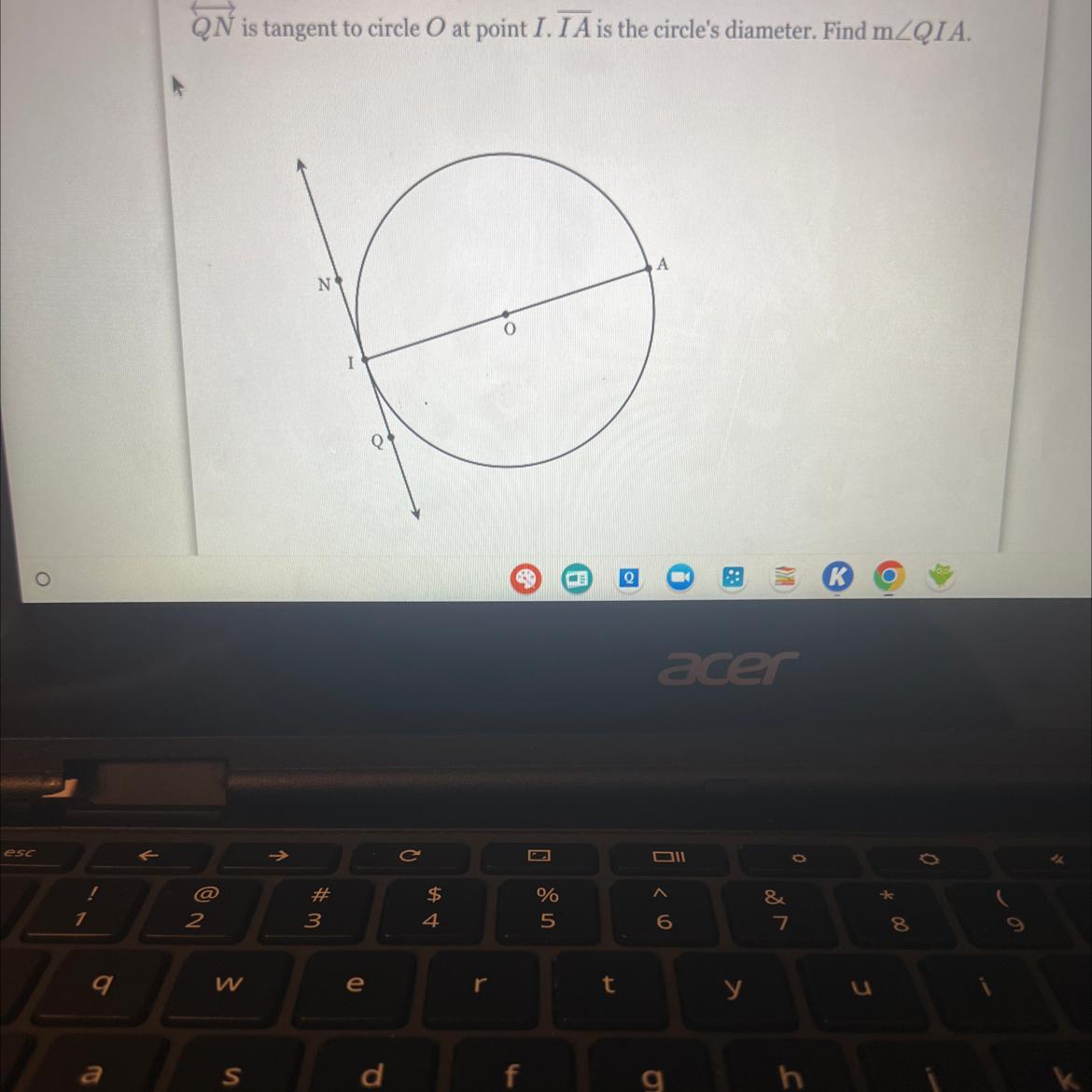
Answers
The measure of tangent angle QIA is 180 degrees.
m/QIA = 180 degrees.
If IA is the diameter of the circle, it means that angle QIA is a right angle (90 degrees). Since QN is tangent to the circle at point I, it is perpendicular to the radius IA at that point.
Therefore, in triangle QIA, we have a right angle at Q and a right angle at I. This implies that angle IQA is also 90 degrees.
In a right triangle, the sum of the angles is 180 degrees. Since angles QIA and IQA are both right angles, the remaining angle in the triangle, angle QAI, must be:
180 degrees - 90 degrees - 90 degrees = 0 degrees
Angle QAI is a degenerate angle, which means it has a measure of 0 degrees. Therefore, the measure of tangent angle QIA is 180 degrees.
To summarize, m/QIA = 180 degrees.
For such more questions on Tangent angle
https://brainly.com/question/30385886
#SPJ11
what is a solution of a system of linear equations in three variables?
Answers
The solution of a system of linear equations in three variables represents the values of the variables that satisfy all the equations simultaneously.
In more detail, a system of linear equations in three variables consists of multiple equations that involve three unknowns. The goal is to find a set of values for the variables that make all the equations true. The solution of such a system can be described as a point or a set of points in three-dimensional space that satisfy all the equations.
In general, there can be three types of solutions for a system of linear equations in three variables:
1. Unique Solution: The system has a single point of intersection, and the values of the variables can be determined uniquely.
2. No Solution: The system has no common point of intersection, meaning there are no values for the variables that satisfy all the equations simultaneously.
3. Infinite Solutions: The system has infinitely many points of intersection, and the values of the variables can be expressed in terms of parameters.
To find the solution of a system of linear equations in three variables, various methods can be used, such as substitution, elimination, or matrix operations. The choice of method depends on the specific characteristics of the equations and the desired approach.
Learn more about infinite solutions here:
brainly.com/question/29093214
#SPJ11
What are the coordinates of the point on the directed line segment from (-1, -2)(−1,−2) to (8, 4)(8,4) that partitions the segment into a ratio of 2 to 1?
Answers
The coordinates which divide the segment with endpoint (-1,-2) and (8,4) in the ratio 2 to 1 are (5,2)
What is section formula?
Section formula is used to find the ratio in which a line segment is divided by a point internally or externally. The section formula can be given as
\((\frac{mx_{2}+nx_{1} }{m+n} ,\)\(\frac{my_{2}+ny_{1} }{m+n})\) where \((x_{1},y_{1} ),(x_{2},y_{2} )\) are the endpoints of the segment and this points are divided in the ratio \(m:n\)
We are given the coordinates as (-1,-2) and (8,4)
This segment is divided in ratio 2:1
We use section formula to find the coordinates
the x- coordinates can be given as
\(x=\frac{2(8)+1(-1)}{2+1}\)
\(x=\frac{16-1}{3}\\\)
\(x=\frac{15}{3}\)
\(x=5\)
Similarly the y coordinate can be given as
\(y=\frac{2(4)+1(-2)}{2+1}\)
\(y=\frac{8-2}{3}\)
\(y=\frac{6}{3}\)
\(y=2\)
Hence the coordinates which divide the segment with endpoint (-1,-2) and (8,4) in the ratio 2 to 1 are (5,2)
To learn more about the section formula please refer
https://brainly.com/question/26433769
#SPJ9
What is the square root of 12654987?
Answers
The square root of 12654987 is approximately 3567.824.
Answer:
3557.38485 . \(\sqrt[2]{12654987}\)
Step-by-step explanation:
The number “ 12654987 “ is NOT a perfect square AT ALL
\(\sqrt[2]{12654987}\) =
3557.38485. ( very weird number to ask… )
