Given: AB- is a line segment with endpoints A(0, 6) and B(8, 0) and point M(4, 3).
Prove: AM- ≅ MB- using the distance formula.
Proof:
• First find the length of AM.
AM = √(x₂ − x₁)² + (Y₂ − y₁)²
= ____
= ____
= ____
= ____
• Next, find the length of MB.
MB = √(x₂ − x₁)² + (Y₂ − y₁)²
= ____
= ____
= ____
= ____
•AM- ≅ MB-
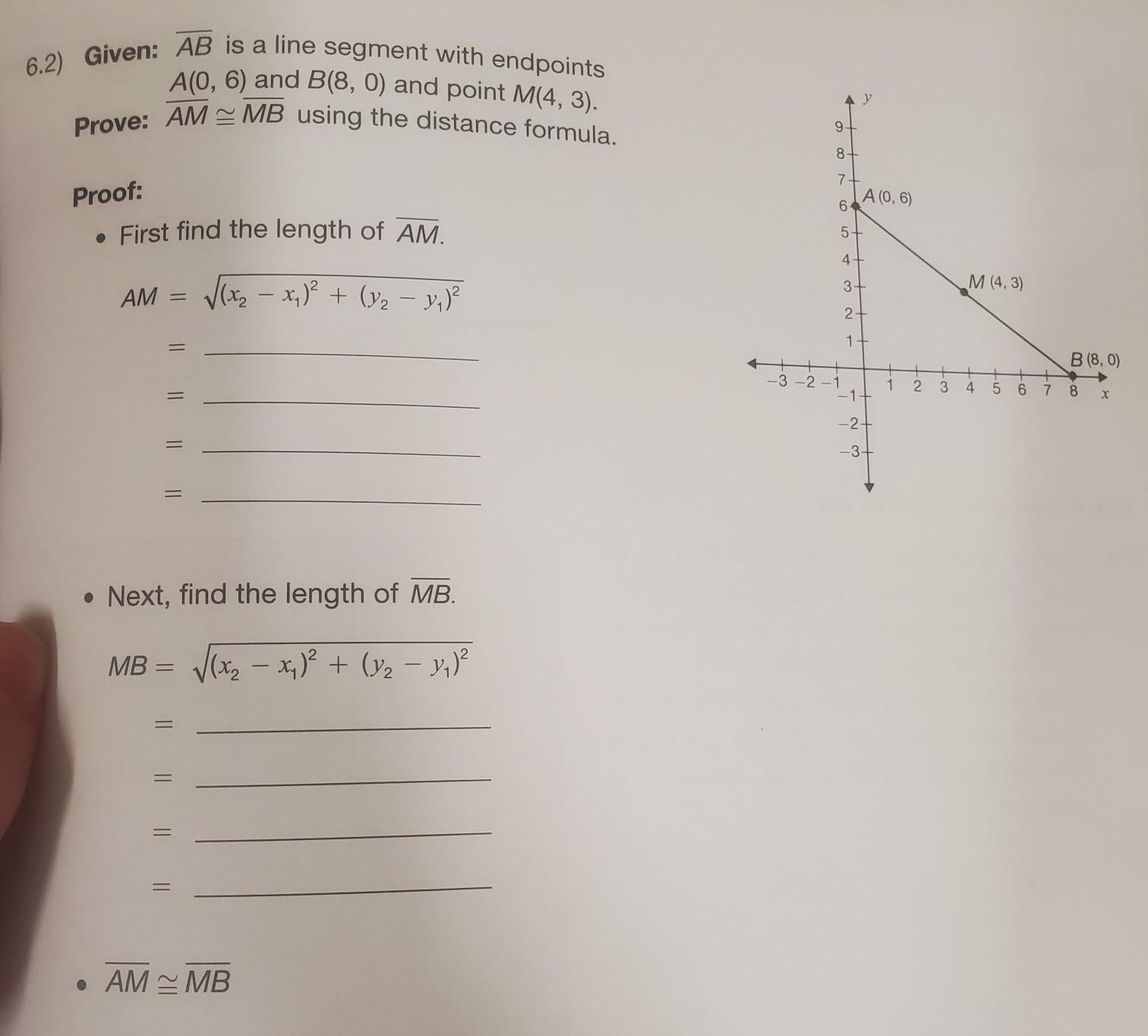
Answers
\(~~~~~~~~~~~~\textit{distance between 2 points} \\\\ A(\stackrel{x_1}{0}~,~\stackrel{y_1}{6})\qquad M(\stackrel{x_2}{4}~,~\stackrel{y_2}{3})\qquad \qquad d = \sqrt{( x_2- x_1)^2 + ( y_2- y_1)^2} \\\\\\ AM=\sqrt{(~~4 - 0~~)^2 + (~~3 - 6~~)^2} \implies AM=\sqrt{( 4 )^2 + ( -3 )^2} \\\\\\ AM=\sqrt{ 16 + 9 } \implies AM=\sqrt{ 25 }\implies \boxed{AM=5} \\\\[-0.35em] ~\dotfill\)
\(~~~~~~~~~~~~\textit{distance between 2 points} \\\\ M(\stackrel{x_1}{4}~,~\stackrel{y_1}{3})\qquad B(\stackrel{x_2}{8}~,~\stackrel{y_2}{0})\qquad \qquad d = \sqrt{( x_2- x_1)^2 + ( y_2- y_1)^2} \\\\\\ MB=\sqrt{(~~8 - 4~~)^2 + (~~0 - 3~~)^2} \implies MB=\sqrt{( 4 )^2 + ( -3 )^2} \\\\\\ MB=\sqrt{ 16 + 9 } \implies MB=\sqrt{ 25 }\implies \boxed{MB=5}\)
Related Questions
find the t-value such that the area under the t distribution to the right of the t-value is 0.10, assuming 15 degrees of freedom (d f).
Answers
The t-value such that the area under the t distribution to the right of the t-value is 0.10, assuming 15 degrees of freedom (df) is 1.753050356.
We have to determine the t-value.
The area in the right tail is 0.10 with 32 degrees of freedom(df).
The t-test is a test that is used as an alternative to the z-test in statistics. If the data are normally distributed but the sample size is small and the population standard deviation is unknown, the t-test is utilized.
A value that appears on the t distribution is the critical t value. The area under the curve and the degrees of freedom can be used to determine the t statistic value.
Using Excel Formula,
The t-value = (=TINV(0.1,15))
The t-value = 1.753050356
To learn more about t-value link is here
brainly.com/question/13574945
#SPJ4
which numbers in the set (2, 3, 4, 5,) are solutions to the inequality 19- 4x>3
Answers
Answer:
2 and 3
Step-by-step explanation:
Given the set (2, 3, 4, 5,) and inequality 19- 4x>3
To obtain which number gives a solution, we test each value in the set ;
19- 4x>3
For x = 2
19- 4(2)>3
19 - 8 > 3
11 > 3 (true)
x = 3
19- 4(3)>3
19 - 12 > 3
7 > 3 (true)
For x = 4
19- 4(4)>3
19 - 16 > 3
3 > 3 (false )
For x = 5
19- 4(5)>3
19 - 20> 3
-1 > 3 (false)
What is the decimal 0.84 (84 repeating) as a fraction? Help pretty please
Answers
Answer:
28/33
Step-by-step explanation:
We first let 0.84 be x.
Since x is recurring in 2 decimal places, we multiply it by 100.
100x=84.84
Next, we subtract them.
100x−x=84.84−0.84
99x=84
Lastly, we divide both sides by 99 to get x as a fraction.
x=84/99
=28/33
Find the area of the triangle below.
Be sure to include the correct unit in your answer.
24 yd
30 yd
18 yd
Answers
The area is 108yd2(square yards).
In the given triangle a base
24yd and the corresponding height of 6 yds are given, so to calculate the area we can use:
A=12×b×h
If we substitute the given numbers we get:
A=\(\frac{1}{2}\)×24×18
=12×9
=108
The units of base and height are the same (yards), so the calculated area is in yd2
The area is the quantity that expresses the extent of a region on the plane or on a curved surface. the world of a plane region or plane area refers to the area of a shape or planar lamina, while area refers to the area of an open surface or the boundary of a three-dimensional object. The area is often understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the quantity of paint necessary to cover the surface with a single coat. it's the two-dimensional analog of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept).
To learn more about the area from the given link:
brainly.com/question/27683633
#SPJ9
Find the geometric mean of 8 and 12, leaving it in simpliest radial form
Answers
The geometric mean of 8 and 12 in the simplest radical form is 4√6
How to determine the geometric mean?From the question, the numbers are given as
8 and 12
These numbers can be represented as
Term 1 = 8
Term 2 = 12
The geometric mean of these numbers is calculated as
Mean = √The product of the terms
Substitute the known values in the above equation, so, we have the following representation
Mean = √8 * 12
Evaluate the products
Mean = √96
Express as radical number
Mean = 4√6
Hence, the geometric mean is 4√6
Read more about geometric mean at
https://brainly.com/question/523830
#SPJ1
Consider the expression 5a + (-2b), where a < 0 and b < a.
Is the sum always positive, always negative, or does it vary?
Support your answer.
Answers
Answer:
positive
Step-by-step explanation:
Lakshmi bought 7 books for a total of 56 rupees how much would see pay for just three books? 56 rupees Indian money
Answers
To find how much would be paid for 3 books, follow the steps below.
Step 01: Find the price of one book.
Let's say the price of one book is x.
Then, the price of 7 books is 7 times x, which is 56 rupes.
\(7x=56\)To find x, let's divide both sides by 7:
\(\begin{gathered} \frac{7x}{7}=\frac{56}{7} \\ 1x=8 \\ x=8 \end{gathered}\)So, the price of one book is 8.
Step 02: Find the price of 3 books.
If the price of one book is 8, the price of 3 books (P) will be 3 times 8:
\(\begin{gathered} P=3\cdot8 \\ P=24 \end{gathered}\)Answer: It would be paid 24 rupees for 3 books.
If the probability that it will rain tomorrow is 0.39 what is the probability that it will not rain tomorrow
Answers
Answer:
0.61
Step-by-step explanation:
probability is out of 100 so if you do 100-39
you get 61
Which of the following conversions is correct?
A. 1 cup is equivalent to 2 pints.
B. 4 pints is equivalent to 1 quart.
C. 1 gallon is equivalent to 128 fluid ounces.
D. 1 quart is equivalent to 8 cups.
Answers
Answer:
C. 1 gallon is equivalent to 128 fluid ounces.
Step-by-step explanation:
Help me plz:(!!!!!!!!!!!

Answers
It’s (10,5) when it comes to this, see where the Line start and then see where it land
Arrange the numbers in decreasing order
Answers
Answer:
arrange them according to the value
Example: Say that the numbers you’re given are 6,0,2,1,8,10
it would be arranged to 10,8,6,2,1,0
Carly’s bake shop requires 3.5 hours of labor to produce one cake and 2 hours of labor to produce one pie, and the shop has a maximum of 70 total labor hours available. If X1 represents number of cakes and X2 represents number of pies, how would this constraint be written?
Answers
Step-by-step explanation:
3.5 hours for 1 cake means 3.5 hours per cake.
similar : 2 hours for 1 pie means 2 hours per pie.
so, if there are e.g. 3 pies, they take 3×2 = 6 hours.
therefore the general constraint is
3.5x1 + 2x2 <= 70
I think the names "x1" and "x2" are confusing when writing this inequality.
I prefer to use x and y.
and then it would look like
3.5x + 2y <= 70
Consider the parabola given by the equation: f(x) = 2x2 + 14.0 – 4
Find the following for this parabola:
A) The vertex:
B) The vertical intercept is the point
C) Find the coordinates of the two z intercepts of the parabola and write them as a list, separated by
commas:
It is OK to round your value(s) to to two decimal places.

Answers
Answer:
Step-by-step explanation:
f(x) = 2x² + 14x - 4
= 2(x² + 7x) - 4
= 2(x² +7x + 3.5²) - 2(3.5²) - 4
= 2(x+3.5)² - 28.5
vertex (3.5, -28.5) = (7/2, -57/2)
The vertical intercept is the y-intercept, i.e., f(0) = -4.
The x-intercepts are the values of x for which y=0.
2x² + 14x - 4 = 0
x = [-14±√(14²-4(2)(-4))]/[2(2)] = [-7±√57]/2 ≅ -7.27, 0.27
5. What is the degree of the following polynomial?
3x³ +9x²-x-10
A.) 4
B.) 5
C.) 3
D.) 6
Answers
Answer:
C
Step-by-step explanation:
the degree of a polynomial is the value of the largest exponent of the variable within the expression.
3x³ + 9x² - x - 10
the term 3x³ has the largest exponent in the expression
the polynomial is therefore of degree 3
What is the local max and min?
Answers
Answer:
Functions can have "hills and valleys": places where they reach a minimum or maximum value. It may not be the minimum or maximum for the whole function, but locally it is.
Step-by-step explanation:
hope this helps :)
Consider the following. fourteen less than the total of a number and three Translate into a variable expression. (Use x for your variable. Do not simplify.)
Answers
9514 1404 393
Answer:
(x +3) -14
Step-by-step explanation:
The total of a number and 3 will be represented by (x +3). Fourteen less than that is ...
(x +3) -14 or -14 +(x +3)
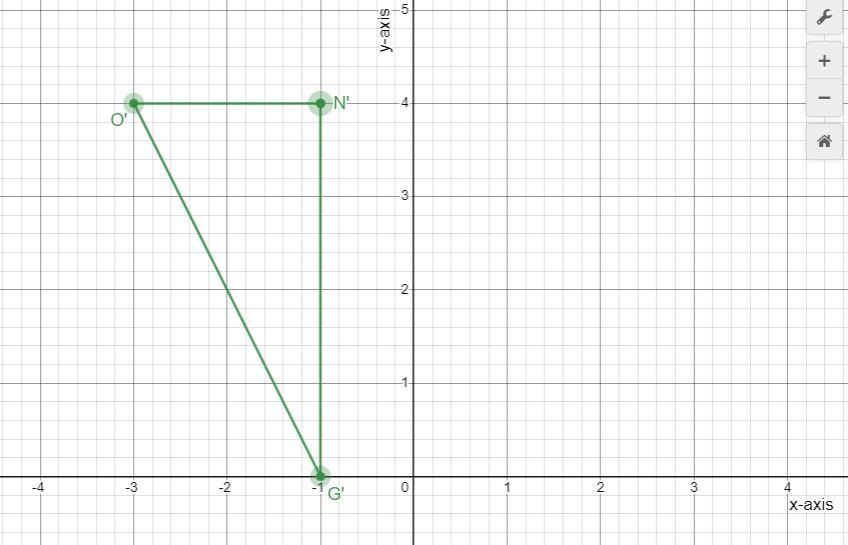
Rotation 90° clockwise about the origin
N
O
G

Answers
An image of triangle NOG after a rotation 90° clockwise about the origin is shown below.
What is a rotation?In Mathematics and Geometry, a rotation is a type of transformation which moves every point of the object through a number of degrees around a given point, which can either be clockwise or counterclockwise (anticlockwise) direction.
Next, we would apply a rotation of 90° clockwise about the origin to the coordinate of this triangle NOG in order to determine the coordinate of its image;
(x, y) → (y, -x)
Point N = (-4, -1) → Point N' (-1, 4)
Point O = (-4, -3) → Point O' (-3, 4)
Point G = (0, -1) → Point G' (-1, 0)
Read more on rotation here: brainly.com/question/28854313
#SPJ1
A restaurant sold 250 drinks in a night. Some of the drinks were sold for $2 each, and the rest for $5 each. If the total sales of drinks for the night was $830, how many $2 drinks were sold?
110
140
145
150
155
?
Answers
Answer:
140
Step-by-step explanation:
Suppose,
x drinks were sold for 2$
y drinks were sold for 5$
therefore, x+y = 250....( 1 )
and 2x+5y = 830......( 2 )
multiply equation ( 1 ) with 2,
2x+2y = 500......( 3 )
Subtract equation ( 3) from (2)
3y = 330
or, y = 110
so, x = 140
so, 140 drinks were sold for 2$
140 drinks were sold for $2.
What are variables and how to define them?A variable is any letter or symbol that represents a number with an unknown value.
We can define them simply by any alphabet like x or y.
What are linear equations and how to make them?A linear equation is generally of the form Ax + By = C, where the two variables are x and y, while A, B and C are constants.
A constant is a value or number that never changes and it's constantly the same.
We have to choose our variables and put them in the equation such that it holds properly and satisfies all the conditions for the given question.
How to solve linear equations?There are several methods of solving linear equations. we may have the linear equation with two or three or many variables. The methods are:
substitution method,elimination method,graphing method.In the given question first, let's make our variables.
Let, the number of drinks was sold for 2$ is x, and the number of drinks was sold for 5$ is y.
And now we will try to make the linear equation with two variables because we have two variables satisfying the conditions in the question given.
One thing to remember carefully is that we have to have two equations if we have two variables.
The restaurant sold a total of 250 drinks so we can write,
x + y = 250
The total sales of drinks for the night was $830 so again we can write,
2x + 5y = 830
Now, we have made the two equations, so we will solve them with help of the substitution method.
Let's, take the equation and just find the value of x,
x + y = 250
x = 250 - y
Now, we will substitute the value of x in the other equation,
2×(250 - y) +5y = 830
Multiplying 2 with the term (250 - y),
500 - 2y + 5y = 830
Now, solve for y,
500 +3y = 830
subtracting 500 both sides we get,
500 - 500 + 3y = 830 - 500
3y = 330
Dividing both sides by 3 we get,
(3y) / 3 = 330 / 3
y = 110
Now, again putting the value of y in the equation x + y = 250 we get,
x + 110 = 250
Subtracting 110 both sides we get,
x + 110 - 110 = 250- 110
x = 140
Now, we can conclude that the number of drinks sold for 2$ is 140 and the number of drinks sold for 5$ is 110.
Therefore, 140 drinks were sold for $2.
To know more about linear equations, making them and solving them click here - brainly.com/question/384631
#SPJ2
find the perimeter of a triangle where one side is 2 inches, one side is 6 inches and another side is 10 inches.
(a) 2in.
(b) 9in.
(c) 36in.
(d) 18in.
Answers
Answer:
(d) 18 in.
Step-by-step explanation:
When we're given the three sides of a triangle, one formula we can use for perimeter of a triangle is:
P = s1 + s2 + s3, where
P is the perimeter,and s1, s2, and s3 are the three sides:P = 2 + 6 + 10
P = 8 + 10
P = 18
Thus, the perimeter of the triangle is 18 in.
What is the distance of line segment AD given the following points, A = -7, B = 5, C = 8, and D = 14?
Answers
Answer:
21
Step-by-step explanation:
Since exact coordinates aren't given, you would have to think of the two points on a number line. The distance from the two points on a number line would be 21. You could also add the absolute values of the two points together. This would basically turn -7 into a positive, and then when the absolute values are added(7 + 14), you would get 21.
Multiply (-4)(-2)(-5)
Answers
Answer:
-40
Step-by-step explanation:
So what this question is basically saying is that you have to multiply -4 by -2 first to get 8 and then you multiply that by -5 hence getting the answer of -40
Which types of transformations do not change the shape of a graph?
Answers
Geometry need help........

Answers
Given :
In triangle AOR and triangle KTE :
Segment AO = Segment KT Segment OR = Segment TE ∠AOR = ∠KTESince two sides and one included angle of these two triangles are equal, we can conclude that these triangles are congruent under the SAS congruence criterion.
5x + 7 =-13 what is x
Answers
Answer:
-4
Step-by-step explanation:
5x=-13-7
5x=-20
x=-20/5
x=-4
Answer:
5x+7=-13
5x=-13-7
5x=-20
x=-20 divide by 5
x=-4
There are 3 car parks, each with 500 spaces in each.
There are 150 spaces in a fourth car park.
How many spaces are there altogether?
Answers
Answer: 1650 spaces
Step-by-step explanation: 500 + 500 + 500= 1500 + 150 = 1650
What type of angle is a 9 degree angle?
Answers
Answer:
An acute angle
Is there any answer choices??
HELP URGENT !!!!!!!!!!!

Answers
What is the simplified form of this expression?

Answers
Answer:
\(=13x+5\)
Step-by-step explanation:
\(\left(2x+9\right)+\left(11x-4\right)\\\mathrm{Remove\:parentheses}:\quad \left(a\right)=a\\=2x+9+11x-4\\\mathrm{Group\:like\:terms}\\=2x+11x+9-4\\\mathrm{Add\:similar\:elements:}\:2x+11x=13x\\=13x+9-4\\\mathrm{Add/Subtract\:the\:numbers:}\:9-4=5\\=13x+5\)
I keep getting the wrong answer.

Answers
The volume of the solid obtained by rotating the region bounded by the curve y = 1 - (x - 5)² in the first quadrant about the y-axis is 51π cubic units.
What is the volume of the solid obtained by rotating the region in the first quadrant bounded by the given curve about the y - axis?To find the volume of the solid obtained by rotating the region bounded by the curve y = 1 - (x - 5)² in the first quadrant about the y-axis, we can use the method of cylindrical shells.
The formula for the volume using cylindrical shells is:
V = 2π ∫ [a, b] x * h(x) dx
Where:
- V is the volume of the solid
- π represents the mathematical constant pi
- [a, b] is the interval over which we are integrating
- x is the variable representing the x-axis
- h(x) is the height of the cylindrical shell at a given x-value
In this case, we need to solve for x in terms of y to express the equation in terms of y.
Rearranging the given equation:
x = 5 ± √(1 - y)
Since we are only interested in the region in the first quadrant, we take the positive square root:
x = 5 + √(1 - y)
Now we can rewrite the volume formula with respect to y:
V = 2π ∫ [c, d] x * h(y) dy
Where:
- [c, d] is the interval of y-values that correspond to the region in the first quadrant
To determine the interval [c, d], we set the equation equal to zero and solve for y:
1 - (x - 5)² = 0
Expanding and rearranging the equation:
(x - 5)² = 1
x - 5 = ±√1
x = 5 ± 1
Since we are only interested in the region in the first quadrant, we take the value x = 6:
x = 6
Now we can evaluate the integral to find the volume:
V = 2π ∫ [0, 1] x * h(y) dy
Where h(y) represents the height of the cylindrical shell at a given y-value.
Integrating the expression:
V = 2π ∫ [0, 1] (5 + √(1 - y)) * h(y) dy
To find h(y), we need to determine the distance between the y-axis and the curve at a given y-value. Since the curve is symmetric, h(y) is simply the x-coordinate at that point:
h(y) = 5 + √(1 - y)
Substituting this expression back into the integral:
V = 2π ∫ [0, 1] (5 + √(1 - y)) * (5 + √(1 - y)) dy
Now, we can evaluate this integral to find the volume
V = 2π ∫ [0, 1] (5 + √(1 - y)) * (5 + √(1 - y)) dy
To simplify the integral, let's expand the expression:
V = 2π ∫ [0, 1] (25 + 10√(1 - y) + 1 - y) dy
V = 2π ∫ [0, 1] (26 + 10√(1 - y) - y) dy
Now, let's integrate term by term:
\(V = 2\pi [26y + 10/3 * (1 - y)^\frac{3}{2} - 1/2 * y^2]\)] evaluated from 0 to 1
V = \(2\pi [(26 + 10/3 * (1 - 1)^\frac{3}{2} - 1/2 * 1^2) - (26 * 0 + 10/3 * (1 - 0)^\frac{3}{2} - 1/2 * 0^2)]\)
V = 2π [(26 + 0 - 1/2) - (0 + 10/3 - 0)]
V = 2π (25.5)
V = 51π cubic units
Learn more on volume of a solid obtained by rotating curve here;
https://brainly.com/question/32301706
#SPJ1
A principal purchased a total of 32 gas cards and movie passes for prizes. Each gas card cost $25.75, and each movie pass cost $7.25. If the principal spent a total of $454.00, how many gas cards did the principal purchase?
Answers
Answer: 12
Step-by-step explanation: 25.75a+7.25b=454
a+b=32