Give the required elements of the hyperbola.
y²/9 - x²/4 =1
The hyperbola opens:
a. Horizontally
b. Vertically
Answers
Step-by-step explanation:
Horizontally.
Cuz if you see the equation or put equation in desmos graph it can open horizontally
Related Questions
2-(3x+5)=5-2x
i have too answers but need the right one lol
Answers
Answer:
x = -8
Step-by-step explanation:
Answer:
Solution given;
2-(3x+5)=5-2x
2-3x-5=5-2x
-3-5=3x-2x
x=-8 is your answer.
Can someone help me please

Answers
9514 1404 393
Answer:
∠Z = 34°
∠T = 56°
Step-by-step explanation:
You can solve for x using the measure of the right angle:
90 = 3x +6
30 = x +2 . . . . . divide by 3
28 = x . . . . . . . . subtract 2
Then the measure of T is ...
∠T = 2x° = 2(28)° = 56°
∠Z is its complement: 90° -56° = 34°
The angle measures are ...
m∠Z = 34°
m∠T = 56°
a sealed ballon filled with air that has a volume of 6 cubic inches at 99 feet will have a volume of
Answers
the volume of the sealed balloon at 33 feet would be 3 cubic inches.
To determine the volume of the sealed balloon at 33 feet, we can apply Boyle's Law, which states that the volume of a gas is inversely proportional to its pressure.
Boyle's Law can be expressed as:
P1 * V1 = P2 * V2
where P1 and V1 are the initial pressure and volume, and P2 and V2 are the final pressure and volume.
In this case, we have:
P1 = pressure at 99 feet
V1 = volume at 99 feet
P2 = pressure at 33 feet
V2 = volume at 33 feet (unknown)
Let's assume the pressure at 99 feet is P1 and the pressure at 33 feet is P2. Since we don't have specific pressure values, we'll use the relative pressure ratios between the two altitudes.
The pressure at higher altitude (99 feet) is lower compared to the pressure at lower altitude (33 feet). Therefore, P1 is less than P2. Let's assume P1 is half of P2.
Now, we can set up the equation:
P1 * V1 = P2 * V2
Let's assume V1 is 6 cubic inches. Then:
(0.5) * 6 = 1 * V2
3 = V2
Therefore, the volume of the sealed balloon at 33 feet would be 3 cubic inches.
Learn more about Boyle's Law here
https://brainly.com/question/21184611
#SPJ4
e ohio lottery has a game called pick 4 where a player pays $1 and picks a four-digit number. if the four numbers come up in the order you picked, then you win $3900. a) write the probability distribution for a player's winnings. fill in the table below. for the computer to grade this one correctly make sure that your x values are from smallest to largest.
Answers
The probability of winning $3,899 is 0.0001, which is a very small probability, but still possible.
To write the probability distribution for a player's winnings in the Pick 4 game, we need to consider all the possible outcomes and their probabilities.
There are a total of 10,000 possible four-digit numbers that can be drawn in the game. Since the player has to match the numbers in the exact order, there is only one winning combination for each four-digit number. Therefore, the probability of winning is 1/10,000.
To calculate the player's winnings, we need to subtract the $1 cost of playing from the $3,900 prize. Thus, the player's net winnings can be calculated as follows:
Net Winnings = $3,900 - $1 = $3,899
The probability distribution for the player's winnings can be summarized in the following table:
| Winnings (x) | Probability (P) |
|--------------|-----------------|
| $0 | 0.9999 |
| $3,899 | 0.0001 |
Note that the table shows the possible winnings (x) in ascending order, as requested. The probability of winning $0 is 0.9999, which means that the player is most likely to lose their $1 bet.
Know more about probability here:
https://brainly.com/question/30034780
#SPJ11
The values in the table represent a function. A 2-column table with 5 rows. The first column is labeled x with entries negative 6, 7, 4, 3, negative 5. The second column is labeled f of x with entries 8, 3, negative 5, negative 2, 12. Use the drop-down menus to complete the statements. The ordered pair given in the first row of the table can be written using function notation as . f(3) is . f(x) = –5 when x is .
Answers
The ordered pair in the row you described would be (6,8), since we write ordered pairs in the form (x,y) and those are the x and y values in the table.
f(3) is asking "What y-value is paired with the x-value of 3?"
f(x) = -5 is asking "What x-value is paired with the y-value of -5?"
Can you read the answers for the last two from your table?
Based on the given table, the ordered pair in the first row is (-6, 8), f(3) is -2, and f(x) = –5 when x is 4.
The ordered pair given in the first row of the table can be written using function notation as (x, f(x)) = (-6, 8).
This is because the first column represents the input values (x) and the second column represents the corresponding output values (f(x)).
f(3) is -2.
This can be determined by finding the value of f(x) when x is 3. According to the table, when x is 3, the corresponding value of f(x) is -2.
f(x) = –5 when x is 4.
This can be determined by finding the value of x when f(x) is -5. According to the table, when f(x) is -5, the corresponding value of x is 4.
To learn more about function click on,
https://brainly.com/question/30537494
#SPJ2
the average (arithmetic mean) of the numbers v, w, x, y, and z is j, and the average of the numbers x, y, and z is k. what is the average of v and w in terms of j and k ?
Answers
Therefore , the solution of the given problem of mean comes out to be value of the mean is 600.
What is mean?A dataset's mean is the sum of all values divided by the total number of values, often known as the arithmetic mean (as opposed to the geometric mean). Often referred to as the "mean," this is the most often used measure of central tendency. Simply dividing the dataset's total number of values by the sum of all of those values yields this result. Both raw data and data that have been combined into frequency tables can be used for calculations. Average refers to a number's average. It is straightforward to calculate: Divide by how many digits there are after adding up all the digits. the total divided by the count.
Here,
Given :The sum is 600.
The average arithmetic mean of x, y and z is 50.
=>(x + y + z)/350, sox + y + z = 150
=>4x + y + 3y+z+32
=>4x+4y+4z 4x+4y+4z4(x+y+ z) 4(x+y+2)
=> 4*150 = 600
To know more about mean visit:
brainly.com/question/30094057
#SPJ4
Write the fraction 16/40 in simplest form. If the fraction is in simplest form
Answers
To covert a fraction to it's simplest form we need to divide their numerator and denominator with the same number .
= 16/40
= 16 ÷ 4 / 40 ÷ 4
= 4/10
= 4 ÷ 2 / 10 ÷ 2
= 2/5
Since both the numerator and denominator dont have a common factor , we can say that they are in their simplest form .
Therefore , the fraction 16/40 = 2/5
Brainliest question please help me now plz

Answers
Answer:
\(\frac{5}{3} \\.3846153846\)
Step-by-step explanation:
true or false, a car engine has an efficiency of about 30%
explain
Answers
A car engine has an efficiency of about 30% is a true statement.
the factual effectiveness of a auto machine can vary grounded on colorful factors similar as machine size, type, and design, as well as driving conditions and conservation. The effectiveness of an machine is a measure of how important of the energy produced by the energy is converted into useful work, similar as turning the bus of a auto.
In an ideal situation, an machine would convert all the energy from the energy into useful work. still, due to colorful factors similar as disunion and heat loss, this isn't possible. The effectiveness of a auto machine is generally calculated by dividing the quantum of energy produced by the energy by the quantum of energy used by the machine. This is known as the boscage thermal effectiveness( BTE) of the machine.
Learn more about efficiency at
https://brainly.com/question/28104222
#SPJ1
10. Set up and evaluate the definite integral for the area of the surface generated by revolving the curve a) (3 pts.)y= 6x 3+ 2x1 ,1≤x≤2, about the x-axis; b) (3 pts.) x= 4y−1,1≤y≤4, about the y-axis.
Answers
The definite integral for the area of the surface generated by revolving the curve y = 6x^3 + 2x about the x-axis, over the interval 1 ≤ x ≤ 2, can be set up and evaluated as follows:
∫[1 to 2] 2πy √(1 + (dy/dx)^2) dx
To calculate dy/dx, we differentiate the given equation:
dy/dx = 18x^2 + 2
Substituting this back into the integral, we have:
∫[1 to 2] 2π(6x^3 + 2x) √(1 + (18x^2 + 2)^2) dx
Evaluating this definite integral will provide the surface area generated by revolving the curve about the x-axis.
b) The definite integral for the area of the surface generated by revolving the curve x = 4y - 1 about the y-axis, over the interval 1 ≤ y ≤ 4, can be set up and evaluated as follows:
∫[1 to 4] 2πx √(1 + (dx/dy)^2) dy
To calculate dx/dy, we differentiate the given equation:
dx/dy = 4
Substituting this back into the integral, we have:
∫[1 to 4] 2π(4y - 1) √(1 + 4^2) dy
Evaluating this definite integral will provide the surface area generated by revolving the curve about the y-axis.
By setting up and evaluating the definite integrals for the given curves, we can find the surface areas generated by revolving them about the respective axes. The integration process involves finding the appropriate differentials and applying the fundamental principles of calculus.
To know more about integral follow the link:
https://brainly.com/question/33191486
#SPJ11
Use the body mass indexes (BMI) for males and use the BMI measure for females listed in the accompanying table to construct boxplots. Use the boxplots to compare the data sets
Answers
By comparing the boxplots, you can observe the differences in the distribution of BMI values between males and females. Look for differences in the medians, interquartile ranges, and any outliers.
To construct boxplots for the body mass index (BMI) data sets for males and females, we first need to gather the necessary information.
To create a boxplot, you need the five-number summary of the data set: minimum value, lower quartile (Q1), median, upper quartile (Q3), and maximum value. These statistics help to visualize the distribution and compare the data sets.
Once you have the five-number summary for both males and females, draw two number lines and place the respective summaries on each line. Then, construct a box around the quartiles and draw lines (whiskers) extending to the minimum and maximum values. This will create two boxplots side by side.
These differences can indicate variations in BMI between the genders.
To know more about boxplots visit:
https://brainly.com/question/24682313
#SPJ11
A cola-dispensing machine is set to dispense 8 ounces of cola per cup, with a standard deviation of 1.0 ounce. The manufacturer of the machine would like to set the control limit in such a way that, for samples of 47, 5% of the sample means will be greater than the upper control limit, and 5% of the sample means will be less than the lower control limit.
If the population mean shifts to 7.8, what is the probability that the change will be detected? (Round your intermediate calculations to 2 decimal places and final answer to 4 decimal places.)
If the population mean shifts to 8.6, what is the probability that the change will be detected? (Round your intermediate calculations to 2 decimal places and final answer to 4 decimal places.)
Answers
1. When the population mean shifts to 7.8, the probability of detecting the change is approximately 0.0495 (or 4.95%).
2. The probability of detecting the change is 0.0495 or 4.95%.
To solve this problem, we'll use the concept of control limits and the sampling distribution of the sample means.
When the population mean shifts to 7.8: First, let's calculate the standard deviation of the sampling distribution, also known as the standard error (SE). The formula for SE is given by SE = σ / sqrt(n), where σ is the standard deviation of the population (1.0 ounce) and n is the sample size (47).
SE = 1.0 / sqrt(47) ≈ 0.145
Next, we need to determine the z-score corresponding to the lower and upper tails of the sampling distribution that capture 5% each. Since the total probability in both tails is 10%, each tail will have a probability of 5%. We can find the z-scores using a standard normal distribution table or calculator.
The z-score corresponding to the lower tail of 5% is approximately -1.645.
The z-score corresponding to the upper tail of 5% is approximately 1.645.
Now, let's calculate the lower and upper control limits:
Lower Control Limit (LCL) = Population Mean - (z * SE)
Upper Control Limit (UCL) = Population Mean + (z * SE)
LCL = 7.8 - (-1.645 * 0.145) ≈ 8.026
UCL = 7.8 + (1.645 * 0.145) ≈ 9.574
To find the probability of detecting the change, we need to calculate the area under the sampling distribution curve that falls beyond the control limits. In this case, we're interested in the area above the upper control limit.
Since the distribution is assumed to be normal, we can use the standard normal distribution's cumulative distribution function (CDF) to calculate this probability.
Probability of detecting the change = 1 - CDF(z-score for UCL)
Using the z-score for the upper control limit (UCL), we can calculate the probability.
Probability of detecting the change ≈ 1 - CDF(1.645) ≈ 0.0495
Therefore, when the population mean shifts to 7.8, the probability of detecting the change is approximately 0.0495 (or 4.95%).
When the population mean shifts to 8.6: We'll follow the same steps as before.
SE = 1.0 / sqrt(47) ≈ 0.145
The z-score corresponding to the lower tail of 5% is still approximately -1.645.
The z-score corresponding to the upper tail of 5% is still approximately 1.645.
LCL = 8.6 - (-1.645 * 0.145) ≈ 8.926
UCL = 8.6 + (1.645 * 0.145) ≈ 10.274
Probability of detecting the change = 1 - CDF(z-score for UCL)
Probability of detecting the change ≈ 1 - CDF(1.645) ≈ 0.0495
Therefore, when the population mean shifts to 8.6, the probability of detecting the change is also approximately 0.0495 (or 4.95%).
In both cases, the probability of detecting the change is 0.0495 or 4.95%.
Learn more about probability from
https://brainly.com/question/30390037
#SPJ11
For the function below find a) the critical numbers; b) the open intervals where the function is increasing, and c) the open intervals where it is decreasing f(x)=8x³-42x-48x + 4 a) Find the critical number(s). Select the correct choice below and, if necessary fill in the answer box to complete your choice. A. The critical number(s) is/are (Type an integer or a simplified fraction. Use a comma to separate answers as needed
Answers
A) Function is increasing on (-∞, -1) and (7/2, ∞), and decreasing on (-1, 7/2).
b) The local minimum value of f is; 5608/2197 at x = -42/13, and the local maximum value of f is 139/8 at x = 7/2.
(a) To determine the intervals on which f is increasing or decreasing, we need to determine the critical points and then check the sign of the derivative on the intervals between them.
f(x)=8x³-42x-48x + 4
f'(x) = 24x² - 90
Setting f'(x) = 0, we get
24x² - 90 = 0
24x² = 90
x =± √3.75
So, the critical points are;
x = -1 and x = 7/2.
We can test the sign of f'(x) on the intervals as; (-∞, -1), (-1, 7/2), and (7/2, ∞).
f'(-2) = 72 > 0, so f is increasing on (-∞, -1).
f'(-1/2) = -25 < 0, so f is decreasing on (-1, 7/2).
f'(4) = 72 > 0, so f is increasing on (7/2, ∞).
Therefore, f is increasing on (-∞, -1) and (7/2, ∞), and decreasing on (-1, 7/2).
(b) To determine the local maximum and minimum values of f, we need to look at the critical points and the endpoints of the interval (-1, 7/2).
f(-1) = -49
f(7/2) = 139/8
f(-42/13) = 5608/2197
Learn more about maximum value here:
brainly.com/question/23504923
#SPJ4
A new brand of gym shoe claims to add up to 2 inches to an athlete’s vertical leaps. Design an experiment to test this claim.
Describe a sample procedure.
A) Find the average vertical leap of all the athletes in their regular shoes. Give the control group the new shoes and the experimental group a different pair of shoes. Find the average vertical leap of the athletes in both groups. Compare the increases in vertical leap for each group.
B) Find the average vertical leap of all the athletes in their regular shoes. Give the experimental group the new shoes and the control group a different pair of shoes. Find the average vertical leap of the athletes in both groups. Compare the increases in vertical leap for each group.
C) Find the average vertical leap of a group of athletes in their regular shoes. Then give them each the new shoes and find their average vertical leap. Compare the before and after results.
Answers
Answer:
The correct option is (B).
Step-by-step explanation:
In this case, we need to test whether the claim made by the new brand of gym shoe is correct or not.
Claim: A new brand of gym shoe claims to add up to 2 inches to an athlete’s vertical leaps.
So, we need to test whether the average vertical leap of all the athletes increased by 2 inches or not after using the new brand of gym shoe.
The sample procedure would be to compute the average vertical leap of a group of athletes in their regular shoes (or a different pair) and the average vertical leap of a group of athletes in their new shoes.
Compare the two averages to see whether the difference is 2 inches or not.
The experimental group would be the one with the new shoes and the control group would be the one with the different pair of shoes.
Thus, the correct option is (B).
Answer:
B) Find the average vertical leap of all the athletes in their regular shoes. Give the experimental group the new shoes and the control group a different pair of shoes. Find the average vertical leap of the athletes in both groups. Compare the increases in vertical leap for each group.
Step-by-step explanation:
whats the area of 8ft, 6ft and 2ft?
Answers
Answer:
96
Step-by-step explanation:
8x6=48
48x2=96
Solve for the missing arcs

Answers
Answer:
Step-by-step explanation:
arc KL = 60°
arc LNK = 360° - 60°
arc NJK = 180°
angle JQN = 60°
arc JN = 60°
arc JM = 60°+55° = 115°
arc MN = 55°
arc MKN = 360° - 55° = 305°
arc JML = 180°
angle MQL = 180° - 55° - 60° = 65°
arc ML = 65°
arc LN = 55° + 65° = 120°
A coordinate grid with 2 lines. The first line is labeled f(x) and passes through (negative 4, 3), (0, 3) and (4, 3). The second line is labeled g(x) and passes through the points (negative 2, negative 5), (0, negative 2), and (2, 1)
Determine the input value for which the statement
f(x) = g(x) is true.
From the graph, the input value is approximately (2) (2.5) (3.5) or (4)
.
f(x) = 3 and g(x) = 3/2x – 2
3 = 3/2x – 2
5 = 3/2x
The x-value at which the two functions’ values are equal is (2/3) (3/2) (5/3) or (10/3)
.

Answers
Answer:
3.5 and 10/3
Step-by-step explanation:
just took the quiz
Answer: C.) 3.5 and D.) 10/3
Step-by-step explanation: i hope this helps :)
A zorb is a large inflated ball within a ball. The formula for the radius r of a sphere with surface area A is given by r=\sqrt((A)/(4\pi )) . Calculate the radius of a zorb whose outside surface area is 49.29 sq m.

Answers
The radius of the zorb with an outside surface area of 49.29 sq m is approximately 1.98 meters.
We are given the surface area (A) of the zorb and asked to find its radius (r) using the formula r = √(A / 4π). Let's follow these steps to solve for the radius:
1. Write down the given information:
A (surface area) = 49.29 sq m
2. Write down the formula for the radius of a sphere:
r = (√A / 4π)
3. Plug in the given surface area (A) into the formula:
r = √(49.29 / 4π)
4. Calculate the value inside the square root:
49.29 / 4π ≈ 3.923
5. Take the square root of the calculated value:
r = √(3.923) ≈ 1.98
So, the radius of the zorb with an outside surface area of 49.29 sq m is approximately 1.98 meters.
For more questions on radius
https://brainly.com/question/18440812
#SPJ11
what is the slope of the line?

Answers
Answer:
The slope is 2/3
Step-by-step explanation:
y is 4 and x is 6 so it will be 4/6 then divide 2
4:2 = 2
6:2 = 3
2/3
A grocery store offers cheese sampler that includes a pepper cheddar cheese that cost $17 per lilogram and pennsylvania jack that cost $11 per kilogram how many kilograms of each were used to make 5 kilogram mixture that cost $12.80 per kilogram
Answers
Answer:
$64.00
Step-by-step explanation:
12.80
x5
_______
$64.00
Answer:
Help
Step-by-step explanation:
how much fat is in a mixture created with x pints of 8% butterfat and y pints of 15% butterfat
Answers
Answer:
Total mixture = (8x + 15y) / 100
Step-by-step explanation:
Butterfat x:
= 8% of x
= 8/100 * x
= (8 * x) / 100
= 8x / 100
Butterfat y:
= 15% of y
= 15/100 * y
= (15 * y) / 100
= 15y / 100
Total mixture = butterfat x + butterfat y
= 8x / 100 + 15y / 100
= (8x + 15y) / 100
Total mixture = (8x + 15y) / 100
Evaluate the expression for
c = 3 and d = -1
cd2

Answers
Answer: 3
Step-by-step explanation:
3(-1)^2
Answer: 3
Step-by-step explanation:
hope this helps
can’t figure this out need help

Answers
i think D hope it helps
Step-by-step explanation:
1 7/8 the least because it farther from the line than 0
Answer:
D. -1 7/8, -1 1/4, -1 1/2, 1
table 6 gives the regression statistics from estimating the model Δln (Salest) = b0 + b1Δln (Salest −1) + εt. table 6 Change in the natural log of Sales for Cisco Systems Quarterly Observations, 3Q:1991–4Q:2000 regression Statistics R-squared Standard error Observations Durbin–watson intercept Δln (Salest −1) Coefficient 0.0661 0.4698 0.2899 0.0408 38 1.5707 Standard error 0.0175 0.1225 t-Statistic 3.7840 3.8339 a. Describe the salient features of the quarterly sales series. b. Describe the procedures we should use to determine whether the ar(1) specification is correct. C. assuming the model is correctly specified, what is the long-run change in the log of sales toward which the series will tend to converge
Answers
As per the regression equation, the value of intercept coefficient is 1.5707
Regression is a statistical technique used to determine the relationship between an independent variable and a dependent variable.
In this case, the regression statistics provided in table 6 show the results of estimating the model
=> Δln (Sales t) = b0 + b1Δln (Sales t −1) + εt,
where Δln (Sales t) is the change in the natural log of sales for Cisco Systems quarterly observations from 3Q:1991 to 4Q:2000.
The R-squared value of 0.0661 indicates that only about 6.61% of the variation in the change in the log of sales can be explained by the change in the log of sales from the previous quarter.
The standard error of 0.4698 indicates the average deviation between the actual and predicted change in the log of sales.
If the results show that the specification is correct, then the long-run change in the log of sales toward which the series will tend to converge can be determined by the intercept coefficient, which in this case is 1.5707.
To know more about regression here.
https://brainly.com/question/14184702
#SPJ4
All students in Ridgewood Junior High School either got their lunch in the school cafeteria or brought it from home on Tuesday. 25% of students brought their lunch. 46 students brought their lunch. How many students in total are in Ridgewood Junior High School?

Answers
Total number of students in Ridgewood Junior High School are 184.
It is given in the question that:-
Number of students who brought their lunch = 46
Percent of students who brought their lunch = 25 %
We have to find the total number of students in Ridgewood Junior High School.
Let the total number of students be 4x.
Hence,
25 percent of 4x = (1/4)*4x = x = Number of students who brought their lunch
We know that 46 students brought their own lunch.
Hence, we can write,
x = 46
Hence,
Total number of students = 46*4 = 184 students.
To learn more about percent, here:-
https://brainly.com/question/28840349
#SPJ1
SOLVE: log x - log (x+4) = -1
Answers
Answer:
x = 4/9
Step-by-step explanation:
Remember when you subtract logs, you divide the numbers;
This means;
log x - log (x+4) = -1 ---------can be written as;
\(log\frac{x}{x+4} =-1\)
Eliminate the log as
\(\frac{x}{x+4} =10^{-1}\)
x/ x+4 = 1/10
10x=x+4 --------collect like terms
10x-x =4
9x = 4 ------find value of x
x= 4/9
How exactly would i find the other three angles?

Answers
Answer:
Opposite interior angles of a rhombus are congruent (the same). All 4 of them equal up to 360
(42 + 20)÷4 − 2·(9÷3) − 2·[18 + 3·(13 − 9) − 5]
hierarchy of operations
Answers
To solve the expression (42 + 20) ÷ 4 - 2 · (9 ÷ 3) - 2 · [18 + 3 · (13 - 9) - 5], we follow the hierarchy of operations known as PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction).
By applying this hierarchy, we can simplify the expression step by step to find the result.
Following the hierarchy of operations, we start by simplifying expressions within parentheses and brackets.
First, within the brackets, we evaluate the expression (13 - 9) which equals 4. Therefore, [18 + 3 · (13 - 9) - 5] becomes [18 + 3 · 4 - 5].
Next, we evaluate the multiplication within the brackets: 3 · 4 equals 12. Thus, [18 + 3 · 4 - 5] simplifies to [18 + 12 - 5].
Moving outside the brackets, we proceed with addition and subtraction: 18 + 12 equals 30, and 30 - 5 equals 25. Therefore, [18 + 12 - 5] becomes 25.
After simplifying the brackets, we can now evaluate the remaining expression: (42 + 20) ÷ 4 - 2 · (9 ÷ 3) - 2 · 25.
Within the parentheses, we perform addition: 42 + 20 equals 62. Thus, the expression becomes 62 ÷ 4 - 2 · (9 ÷ 3) - 2 · 25.
We continue by evaluating the division: 62 ÷ 4 equals 15.5. The expression now becomes 15.5 - 2 · (9 ÷ 3) - 2 · 25.
Next, we perform the division within the parentheses: 9 ÷ 3 equals 3. The expression becomes 15.5 - 2 · 3 - 2 · 25.
Finally, we evaluate the remaining multiplications: 2 · 3 equals 6, and 2 · 25 equals 50. The expression becomes 15.5 - 6 - 50.
Continuing with the subtraction, we have 15.5 - 6 equals 9.5. Therefore, the final result of the expression (42 + 20) ÷ 4 - 2 · (9 ÷ 3) - 2 · [18 + 3 · (13 - 9) - 5] is 9.5.
Learn more about PEMDAS here:
https://brainly.com/question/29172059
#SPJ11
the integral test can be used to conclude that which of the following statements about the infinite series ∑n=2[infinity]1nlnn is true? A The series converges, and the terms of the series have limit 0. B) The series diverges, and the terms of the series have limit o. с The series converges, and the terms of the series do not have limit o. D The series diverges, and the terms of the series do not have limit 0
Answers
Therefore, the correct answer is B) The series diverges, and the terms of the series have limit o.
The integral test is a powerful tool used to determine whether an infinite series converges or diverges. The integral test states that if an infinite series has a non-negative and decreasing term, then the series is convergent if and only if the corresponding integral is convergent. In the case of the series ∑n=2[infinity]1nlnn, we can apply the integral test by considering the function f(x) = 1/xlnx. This function is decreasing and positive for all x > 2. Therefore, we can integrate f(x) from 2 to infinity to obtain the integral ∫2[infinity]1/xlnx dx. Evaluating this integral, we get ln(lnx)|2[infinity], which diverges. Since the integral diverges, we can conclude that the series ∑n=2[infinity]1nlnn also diverges.
To know more about infinite visit:
https://brainly.com/question/30790637
#SPJ11
Exit
From the information in the graph, what is the mean number of books the girls read?
A. 3
B. 4
C. 5
D. 6
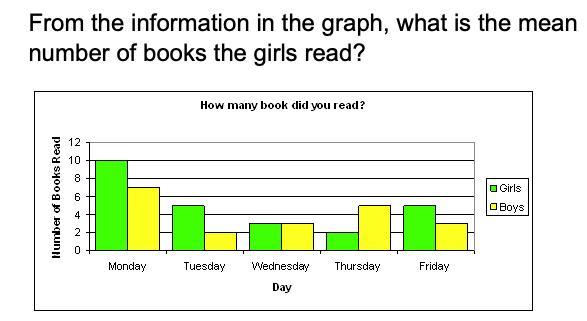
Answers
Answer:
C
Step-by-step explanation:
\( \frac{10 + 5 + 3 + 2 +5 }{5} = \frac{25}{5} = 5\)