ggggtreeewwqaaasffgggggyyyttttrffrrrrrff
Answers
Related Questions
The shed will have a flat un-evenly sloped roof. One corner is 12 feet high and two others are 10 feet high. What is the volume of the shed
Answers
Therefore, based on these assumptions, the approximate volume of the shed is 1600.5 cubic feet.
To calculate the volume of the shed, we need to know the dimensions of the shed. However, based on the given information about the roof heights.
we can make some assumptions and provide a general approach to estimating the volume.
Assuming the shed has a rectangular base, we can approximate the volume by multiplying the base area by the average height. Let's assume the shed has dimensions length (L), width (W), and average height (H).
Given that one corner is 12 feet high and two other corners are 10 feet high, we can estimate the average height (H) as the average of these three heights:
H = (12 + 10 + 10) / 3 = 32 / 3 ≈ 10.67 feet
Now, let's consider the base of the shed. Since it is rectangular, we can assume the length (L) and width (W) based on your knowledge of the shed's dimensions. Let's say L = 15 feet and W = 10 feet.
The volume of the shed can be approximated as:
Volume ≈ Base Area × Average Height
≈ L × W × H
≈ 15 ft × 10 ft × 10.67 ft
≈ 1600.5 cubic feet
Keep in mind that this estimation may not be accurate if the actual shape or dimensions of the shed differ significantly from the assumptions made.
Learn more about estimating here:
https://brainly.com/question/30870295
#SPJ11
10+8÷2(4+3) simplify the expression using the order of operation
Answers
Answer:
truly ez points
Step-by-step explanation:
find the value of each variable

Answers
The value of the sides are;
x = 13
y = 13 √2
How to determine the valueTo determine the value of the identities, we have to note the know the trigonometric identities. They are;
sinecosinetangentsecantcosecantcotangentFrom the information given, we have that;
Using the tangent identity;
tan θ = opposite/adjacent
substitute the values, we get
tan 45 = x/13
cross multiply the values
x = 13
Using the sine identity
sin 45 = 13/y
y = 13 √2
Learn about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
Quan can make 30 bracelets in 2.25 hours. How much time will it take him to make 80 bracelets .
Answers
Answer:
6
Step-by-step explanation:
Marcus had $21 to spend on two posters. After buying them he had $13. How much did each poster cost?
Answers
Answer:
$4
Step-by-step explanation:
Each poster cost $4 because $21 - $13 is $8 and you said he bought 2 posters so $8 divided by 2 is $4
find the area of the surface obtained by rotating the curve y=x−−√3y=x3 about yy-axis for 1≤y≤41≤y≤4.
Answers
Thus, the area of surface obtained by rotating the curve y=x−−√3y=x3 about the y-axis for 1≤y≤4 is 36π√3 square units.
To find the area of the surface obtained by rotating the curve y=x−−√3y=x3 about the y-axis for 1≤y≤4, we can use the formula:
A = 2π ∫(1 to 4) x √(1+(dy/dx)^2) dy
First, we need to find dy/dx by taking the derivative of y=x−−√3y=x3:
dy/dx = 1/(2√3x^(1/2))
Substituting this into the formula, we get:
A = 2π ∫(1 to 4) x √(1+1/(12x)) dy
Simplifying the expression under the square root, we get:
A = 2π ∫(1 to 4) x √(12x+1)/12 dy
We can simplify this expression further by using a substitution u = 12x+1:
A = π ∫(13 to 49) √u du
Integrating this, we get:
A = π (2/3)(u^(3/2))|(13 to 49)
A = π (2/3)(49√49-13√13)
A = 36π√3 square units
Therefore, the area of the surface obtained by rotating the curve y=x−−√3y=x3 about the y-axis for 1≤y≤4 is 36π√3 square units.
Know more about the derivative
https://brainly.com/question/28376218
#SPJ11
Design a situation where the probability of one event is 1/5 and another event is 1/10
Answers
We have designed a situation where the probability of one event (event A) is 1/5 and the probability of another event (event B) is 1/10.
How to quantify probability?To quantify the probability of each event, we can define the following events:
Event A: selecting a unit of product A at random and finding that it is defective.Event B: selecting a unit of product B at random and finding that it is defective.Then, the probability of event A is 1/5, since 1 in every 5 units of product A is defective. Similarly, the probability of event B is 1/10, since 1 in every 10 units of product B is defective.
Now, let's consider a scenario where the company receives an order for 100 units of products, with 60 units of product A and 40 units of product B. The company wants to determine the probability of the following events:
Event C: selecting a unit from the order at random and finding that it is defective.Event D: selecting a unit from the order at random and finding that it is not defective.To calculate the probability of event C, we need to consider the probability of selecting a defective unit from product A and from product B, and the proportion of each product in the order. Since the order has 60 units of product A and 40 units of product B, the probability of selecting a unit of product A is 60/100 = 3/5, and the probability of selecting a unit of product B is 40/100 = 2/5.
Using the probabilities of event A and event B, we can calculate the probability of selecting a defective unit from product A or from product B as follows:
Probability of selecting a defective unit from product A: 1/5Probability of selecting a defective unit from product B: 1/10Therefore, the probability of event C can be calculated as follows:
P(C) = P(A) * P(A in order) + P(B) * P(B in order)
= (1/5 * 3/5) + (1/10 * 2/5)
= 3/25
So the probability of selecting a defective unit from the order is 3/25.
To calculate the probability of event D, we can use the complement rule, which states that the probability of an event and its complement (i.e., the event not happening) add up to 1. Therefore, the probability of event D can be calculated as follows:
P(D) = 1 - P(C)
= 1 - 3/25
= 22/25
So the probability of selecting a unit from the order at random and finding that it is not defective is 22/25.
In summary, we have designed a situation where the probability of one event (event A) is 1/5 and the probability of another event (event B) is 1/10. We have also calculated the probability of two other events (event C and event D) in a scenario where a manufacturing company produces two types of products, with different probabilities of defects, and receives an order with a certain proportion of each product.
To know more about probability visit:
brainly.com/question/25870256
#SPJ1
$7 for adult addmison and $5 for a child addmison and $3 for an adult and $2 for child for the boat ridesTrina and Juan and their father have $33 to spend at the water park Trina and juan qualify for a child's addmision how many times can all 3 go on a boat ride
Answers
By using addition, it can be calculated that
Trina, Juan and their father can do one boat ride.
What is addition?
Suppose there are many numbers and we need to find the sum total of all those numbers, then the operation used in this case is called addition.
This is a word problem on addition
Cost of adult admission = $7
Cost of child admission = $5
Cost of boat ride for adult = $3
Cost of boat ride for child = $2
Total expense for adult = $(7 + 3) =$10
Total expense for child = $(5 + 2) =$7
Trina and Juan and their father have $33 to spend at the water park
Trina and Juan qualify for a child's admission
Total expense for one boat ride = $(7 + 7 + 10) = $24
Total expense for two boat rides = $(24 + 24) = $48
But they have $33 to spend
So Trina, Juan and their father can do one boat ride.
To learn more about addition, refer to the link-
https://brainly.com/question/24536701
#SPJ4
Write equations for the horizontal and vertical lines passing through the point (-2,-5).
Answers
Answer:
y = -5x = - 2=============================
The horizontal line has same y- coordinate for each x- coordinate, and is parallel to the x-axis so it is:
y = - 5The vertical line has same x- coordinate for each y- coordinate, and is parallel to the y-axis so it is:
x = - 2Refer to graphs.

I need this answer ASAP! Please help!
A ladder is leaning against a building. The ladder forms an angle of 77° with the ground. The distance from the base of the ladder to the base of the building is 8 feet.

Answers
Answer:
Step-by-step explanation:
sin77=h/8
h=8sin77
h=8(0.9744)
h=7.7952ft
Is a triangle possible with length of the sides as 10. 2 cm 6. 8 cm and 4. 6 cm?.
Answers
Yes, it is possible to draw a triangle.
This will be done by the property: the sum of two sides of a triangle should be more than the third side.
(4.6cm + 6.8cm) =10.2cm
11.4cm = 10.2cm
LHS>RHS
A triangle is possible.
A triangle is a polygon with three edges and 3 vertices. The terminology for categorizing triangles is more than two thousand years vintage, having been defined on the first actual page of Euclid's elements.
In Euclidean geometry, any three factors, while non-collinear, decide a completely unique triangle and simultaneously, a unique plane (i.e. a -dimensional Euclidean space). In different words, there's best one plane that consists of that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is the best one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is not real. this text is ready triangles in Euclidean geometry, and in particular, the Euclidean plane, except wherein otherwise stated.
To learn more about Triangle visit here:
brainly.com/question/2773823
#SPJ4
Okay im learning algebra right now and this question hit my head here, its asked which expression was equivalent to this 2v+6v+3c. here are the answer 2v + 9c / 8v + 3c / 11vc / 11+ v+ c
Answers
Answer:
8v+3c
Step-by-step explanation:
Given 2v+6v+3c
1) Add all like terms
-Since both 2 and 6 have "v" and the two together
2) 8v+3c
Answer: 8v+3c
Hope this helps :)
What are the vertices of C'D'E ?

Answers
Answer:
C(-8, 1)
D(-6, 5)
E(-2, 4)
Step-by-step explanation:
You make the y value opposite if you reflect over the x axis
Answer:
C(-8, 1), D(-6, 5), E(-2, 4)
Step-by-step explanation:
A fair 6-sided die is rolled 300 times. What is a reasonable prediction for the number of times the event of landing on an odd number will occur?
A. 150
B. 50
C. 175
D. 100
Answers
Answer:
A. 150
Step-by-step explanation:
Calculate the probability of landing on an odd number: 1/2.
Multiply the probability by the number of trials: (1/2) * 300.
Simplify the expression: 150.
Therefore, a reasonable prediction is that the event of landing on an odd number will occur 150 times out of the 300 rolls of the fair 6-sided die.
14 POINTS GIVEN‼‼‼
I dont know what this means

Answers
The prism has 22 faces and the expression for the number of faces the prism has is n + 2 faces
a. The prism has 22 faces
b. The expression is n + 2
How many faces does a prism with a cross-section that has a 20-sided polygon have?a. A prism with a cross-section that is a 20-sided polygon will have two additional faces apart from the 20 faces of the polygon. Therefore, the prism will have a total of 22 faces.
b. If a prism has a cross-sectional face that is a polygon with n sides, the prism will have n + 2 faces. The additional two faces are the top and bottom faces of the prism.
Using this expression, we can determine the number of faces for any prism based on the number of sides in its cross-sectional polygon.
Learn more on prism here;
https://brainly.com/question/8839626
#SPJ1
A website is selling houseplants for $5. The
site got the houseplants at a cost of $4.
What is the mark-up percentage?
Answers
Answer:
125 percent
Step-by-step explanation:
Divide the website selling price by the original cost
5/4 = 1.25
Move the decimal to the right twice to make a percent
125 percent
Can someone please help me with math.

Answers
Answer:
The answer is 2/10 which simplifies to 1/5
I don't know the second one:(
The Volume
of a cube
is 788cm³. Work out the
length of its Side
rounded to 1
decimal point
Answers
Answer:
9.2 cm
Step-by-step explanation:
A cube has all the dimensions L W and D the same
Volume = L x W X D
= L^3 = 788 <===== take cube root of both sides
L = 9.2 cm
Please help me with this

Answers
Each tile has a surface area of 1 × 1 = 1 square foot since each tile is 1 foot long. As a result, the total mosaic's area is 49 x 1, or 49 square feet.
what is surface area ?The overall area that a three-dimensional object's surface occupies is known as surface area. Square units like square inches, square meters, and square feet are used to convey it. By adding up the areas of all the object's faces or surfaces, surface area is determined. By summing the areas of the cube's six faces, for instance, it is possible to get the surface area of a cube.
given
There are 7 rows and 7 tiles in the mosaic, making a total of 7 x 7 = 49 tiles in the mosaic.
Each tile has a surface area of 1 × 1 = 1 square foot since each tile is 1 foot long.
As a result, the total mosaic's area is 49 x 1, or 49 square feet.
To know more about surface area visit:
https://brainly.com/question/2835293
#SPJ1
The complete question is:- Mark's window store made a mosaic for the community center. The mosaic had a 7 x 7 array of different color square tiles. If each tile is 1ft long, what is the area of the whole mosaic?
Can someone explain how to do this?

Answers
Answer:
118,900,000,000,000 (1.189 × 10^14)
Step-by-step explanation:
First, assume that a cell is roughly a sphere with radius 10−³cm (. Let's compute the volume of the cell from the relation between radius and volume:
The volume V of a sphere with radius r is
V=(4π)/3 r³
where r³ and V have the same units. The volume of a cell with radius 10−³cm is therefore
V=4π³/3(10−³)3≈4.1888×10−⁹ cm³.
Next, we use the fact that the density of a cell is approximately the density of water which is 1g/cm³. Let's compute the mass of a cell from its volume and density using the definition of density:
density = mass/volume
which is equivalent to
mass = density×volume.
The mass of a cell is therefore
1 (g)/cm³×4.1888×10−⁹cm³ ≈ 4.1888×10−⁹g.
Now you know the mass of a cell, what other piece of information do you need to work out the number of cells in your body? Your mass in grams (if you know your weight in pounds, you can convert: 1 lb≈453.6 grams).
Number of cells=Your Mass/Mass of Cell
For example, the mass of a 175 lb is about 45,360 grams. We have that
79378g/4.1888×10−⁹g≈11.89 × 10^14
so there are approximately 1×10¹⁴=118,900,000,000,000 (1.189 × 10^14) cells in the human body!
please help me I will mark BRAINLIEST and I will give you a rating of 5 stars

Answers
Answer:
141 = 145 184-188
Step-by-step explanation:
to find the pattern you would have to see what each of them have in common
All of them 4 was added to the answer
I subtracted both numbers and got 4 then i decided to add 4 to get the other to get the pattern
The area of Kamila’s rectangular living room is 2.5 times the area of her square bedroom. The length of the living room is 18 feet and its width is 1.25 times the length of a side of the bedroom.Create a diagram representing Kamila’s living room and her square bedroom. Assign variables to any unknown sides and label the diagram.Find the length of one side of Kamila’s bedroom.In your final answer, include your diagram, and all formulas, equations, and calculations necessary to solve for the length of Kamila’s bedroom.
Answers
Answer:
The length of each side of Kamila’s square bedroom is;
\(9\text{ feet}\)For the Living room;
\(\begin{gathered} A_l=18\times1.25x \\ A_l=22.5x\text{ --------1} \end{gathered}\)For the bedroom;
\(\begin{gathered} A_b=x\times x \\ A_b=x^2\text{ -----------2} \end{gathered}\)Recall that the area of Kamila’s rectangular living room is 2.5 times the area of her square bedroom;
\(A_l=2.5A_b\text{ ----------3}\)Explanation:
Given that the area of Kamila’s rectangular living room is 2.5 times the area of her square bedroom. The length of the living room is 18 feet and its width is 1.25 times the length of a side of the bedroom.
Recall that the area of a rectangle can be calculated using the formula;
\(A=l\times b\)For the Living room;
\(\begin{gathered} A_l=18\times1.25x \\ A_l=22.5x\text{ --------1} \end{gathered}\)For the bedroom;
\(\begin{gathered} A_b=x\times x \\ A_b=x^2\text{ -----------2} \end{gathered}\)Recall that the area of Kamila’s rectangular living room is 2.5 times the area of her square bedroom;
\(A_l=2.5A_b\text{ ----------3}\)substituting equations 1 and 2 into equation 3;
\(\begin{gathered} A_l=2.5A_b\text{ ----------3} \\ 22.5x=2.5(x^2) \\ x=\frac{22.5}{2.5} \\ x^{}=9 \\ x=9\text{ feet} \end{gathered}\)Therefore, the length of each side of the square bedroom is;
\(9\text{ feet}\)

This figure shows the dimensions of a rail car. The car forms a cylinder with a length of 24 feet and radius of 4 feet.
What is the volume, in cubic feet, of the car? Round your answer to the nearest hundredth.
Answers
Answer:
1206.857, cubic feet
Step-by-step explanation:
(22/7×4²)×24
=1206.857 cubic feet
make y the subject
y-aw=2w-1
Answers
Answer:
y = 2w - 1 + aw
Step-by-step explanation:
Given
y - aw = 2w - 1 ( isolate y by adding aw to both sides )
y = aw - 1 + aw
Determine the equation of the circle with center ( 3 , 9 ) containing the point ( 8 , − 3 )
Answers
Answer:
see the answer in the picture
Step-by-step explanation:
I don't know which equation you want. but I put both the standard and general form. but the equation should be the stander form. the radius is 13 in this case



We will see that this circle is centered at the point (-5, -49) and has a radius of 1.
What is the general circle equation?For a circle of radius R centered at the point (a, b), the equation is:
(x - a)^2 + (y - b)^2 = R^2
In this case, we have:
given the equation of the circle is
x^2 + y^2 + 10x + 14y + 73 = 0
We can rewrite this as:
(x^2 + 10x) + (y^2 + 14y) + 73 = 0
(x^2 + 2*5*x + 25) + (y^2 + 2*7*y + 49) - 25 - 49 + 73 = 0
(x + 5)^2 + (y + 49)^2 -74 + 73 = 0
(x + 5)^2 + (y + 49)^2 = 1
So we have a circle centered at the point (-5, -49) with a radius equal to 1.
If you want to learn more about circles, you can read:
brainly.com/question/25306774
#SPJ2
complete question:
Determine the center and radius of the following circle equation
x^2 + y^2 + 10x + 14y + 73 = 0
PLS PLS i need step by step please and undefined numbers to be shown please THANK YOU!

Answers
1)The expression 4x^2-16x+12/x^2-9 is undefined when the denominator, x^2-9, equals zero because division by zero is undefined.
x^2-9 equals zero when x equals 3 or x equals -3. Therefore, the expression is undefined at x = 3 and x = -3. In all other cases, the expression is defined.
2) The given expression is:
(5-2x)/(x+2) + x^2/(x^2-4) - 5
To simplify this expression, we need to first find the LCD (least common denominator) of the two fractions. The denominator of the first fraction is x+2, and the denominator of the second fraction is x^2-4, which can be factored as (x+2)(x-2). So the LCD is (x+2)(x-2). Now we can rewrite the expression with this common denominator:
[(5-2x)(x-2) + x^2(x+2) - 5(x+2)(x-2)] / [(x+2)(x-2)]
Expanding the brackets and simplifying, we get:
(-x^3 - 3x^2 - 3x + 5) / [(x+2)(x-2)]
This expression is undefined when the denominator, (x+2)(x-2), equals zero because division by zero is undefined.
(x+2)(x-2) equals zero when x equals -2 or x equals 2. Therefore, the expression is undefined at x = -2 and x = 2. In all other cases, the expression is defined.
#SPJ1
the question is
what is the distribution of the graph? explain how you know
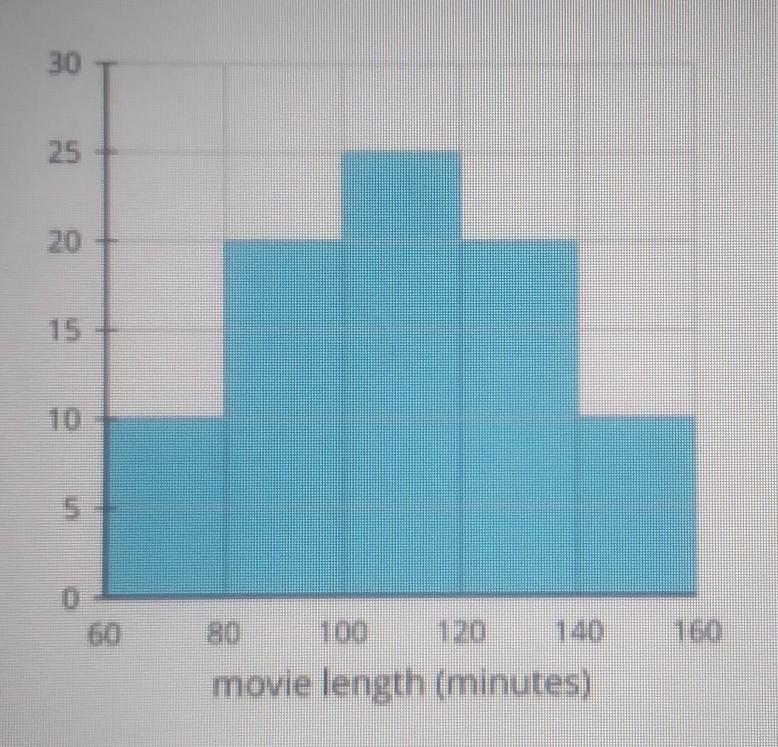
Answers
Answer:
Pyramid Distribution
Step-by-step explanation:
I don't know the answers but from what I know it has to be pyramid distribution or triangle distribution Hope This Helps!
How to do this question

Answers
Answer:
1/17
Step-by-step explanation:
You're on the right track so far!
(2³ + 3²) ⁻¹
= (8 + 9) ⁻¹
= (17) ⁻¹
= 1/17 (Remember, (a)⁻ⁿ = 1 / aⁿ)
Hi there!! (✿◕‿◕)
⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐
A = 2 B = 3
(a^b + b^a)^-1
(2^3 + 3^2)^-1
1/7 or 0.058824
Hope this helped!! ٩(◕‿◕。)۶
what is the largest of three consecutive integers if the sum of the two larger integers is 3 more than two times the smallest integer
Answers
Answer:
Ambitious Ambitios Ambitious Ambitions
Given f(x)=x^2 +4x and g(x)= 2x +3 , evaluate each expression. f(g(2))
Answers
Answer: 77
Step-by-step explanation:
\(g(2)=2(2)+3=7 \\\\\implies f(g(2))=f(7)\\\\f(7)=7^2 +4(7)=49+28=77\)