f(x) = x to the power of 2 + 4 (x=3)
evaluate
Answers
Answer:
13
Step-by-step explanation:
Related Questions
What is the diffrence between 2 and 3.
Answers
Step-by-step explanation:
The difference between 2 and 3 is 1.
Answer:
1
Step-by-step explanation:
To find the difference between 2 and 3, you can literally count from 2 to 3. There is 1 number difference because it goes:
2, 3
Therefore, the answer is 1
What is the value of the expression? 8.5 - (-4.8) - 7
Answers
Answer:
6.3
Step-by-step explanation:
8.5 - (-4.8)
Let's focus on - (-4.8)
if a negative number is subtracted, it reverses itself
In other words, if a negative number is being subtracted, it is the same as being added as a positive number
So we change the equation to
8.5 + 4.8 = 13.3
Now we subtract 7 from 13.3
Since positive 7 is being subtracted, the rule for -4.8 does not apply to it
13.3 - 7 = 6.3
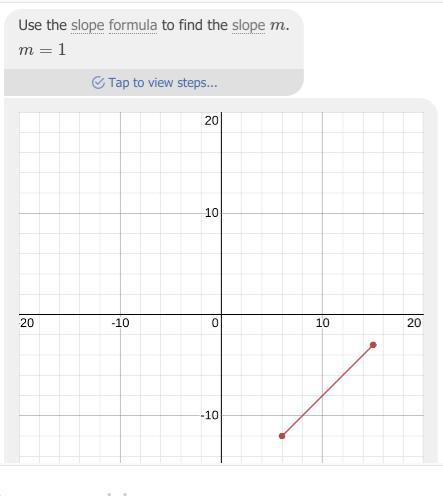
(6.-12) & (15,-3)
Need to find slope
Answers
Answer:
i look it up
Step-by-step explanation:
Solve (−7) ⋅ (−4). Please hurry :D
-28
-11
28
11
Answers
Answer:
28
Step-by-step explanation:
\( - (7) \times ( - 4) \\ - ( - 28) \\ - \times - = + \\ = 28\)
help please! anyone know how to graph this

Answers
Answer:
The grpah should help!

Answer:
See attached for graph of the given function.
Step-by-step explanation:
Vertex form of a quadratic function
\(f(x)=a(x-h)^2+k\)
where:
(h, k) is the vertex.a is some constant to be found.If a>0 the parabola opens upwards.
If a<0 the parabola opens downwards.
Given function:
\(g(x)=-\dfrac{1}{5}(x+5)^2-2\)
Vertex
Comparing the given function with the vertex formula:
\(\implies h=-5\)
\(\implies k=-2\)
Therefore, the vertex of the parabola is (-5, -2).
As a<0, the parabola opens downwards. Therefore, the vertex is the maximum point of the curve.
Axis of symmetry
The axis of symmetry is the x-value of the vertex.
Therefore, the axis of symmetry is x = -5.
y-intercept
To find the y-intercept, substitute x = 0 into the given function:
\(\implies f(0)=-\dfrac{1}{5}(0+5)^2-2=-7\)
Therefore, the y-intercept is (0, -7).
x-intercepts
To find the x-intercepts, set the function to zero and solve for x:
\(\implies -\dfrac{1}{5}(x+5)^2-2=0\)
\(\implies -\dfrac{1}{5}(x+5)^2=2\)
\(\implies (x+5)^2=-10\)
As we cannot square root a negative number, the curve does not intercept the x-axis.
Additional points on the curve
As the axis of symmetry is x = -5 and the y-intercept is (0, -7), this means that substituting values of x in multiples of 5 either side of the axis of symmetry will yield integers:
\(\implies f(-10)=-\dfrac{1}{5}(-10+5)^2-2=-7\)
\(\implies f(5)=-\dfrac{1}{5}(5+5)^2-2=-22\)
\(\implies f(-15)=-\dfrac{1}{5}(-15+5)^2-2=-22\)
Therefore, plot:
vertex = (-5, -2)y-intercept = (0, -7)points on the curve = (-10, -7), (5, -22) and (-15, -22)axis of symmetry: x = -5Draw a smooth curve through the points, using the axis of symmetry to ensure the parabola is symmetrical.

how do you Write sin34 in terms of cosine.
Answers
sin(θ) = cos(90 - θ)
sin(34) = cos(90 - 34)
sin(34) = cos(56)
So the answer would be 56 basically
in multiple regression analysis, a variable that cannot be measured in numerical terms is called a group of answer choices nonmeasurable random variable. constant variable. dependent variable. categorical independent variable.
Answers
In multiple regression analysis, a variable that cannot be measured in numerical terms is called a categorical independent variable.
This type of variable is usually represented by non-numerical data, such as names, categories, or labels. Unlike numerical variables, categorical variables cannot be measured in units or values, but rather they represent different groups or categories. For instance, a categorical independent variable could be gender, race, or occupation.
These variables are included in regression analysis as dummy variables, which take on the value of 0 or 1, depending on whether the observation belongs to a specific category or not. It is important to note that while categorical variables cannot be measured numerically, they still play an important role in predicting the dependent variable in regression models.
Learn more about variable here:
brainly.com/question/16601895
#SPJ11
A pair of speakers costs 3 times as much as a pair of headphones. A camera costs 36 more than a pair of speakers. The total cost of the three items is £155. How much does each item cost?
Answers
The cost of each pair of speakers, pair of headphones and camera is £17, £51 and £87 respectively.
How much does each item cost?Let
cost of each headphones = x
cost of each speaker = 3x
cost of a camera = 3x + 36
Total cost = £155
Total cost = cost of each headphones + cost of each speaker + cost of a camera
155 = x + 3x + 3x + 36
155 = 7x + 36
subtract 36 from both sides
155 - 36 = 7x
119 = 7x
divide both sides by 7
x = 17
Therefore,
cost of each headphones = x
= £17
cost of each speaker = 3x
= 3×17
= £51
cost of a camera = 3x + 36
= 51 + 36
= £87
Read more on cost of each item:
https://brainly.com/question/30205161
#SPJ1
If a=21m and c=35m what is the length of side b using the pythagorean
theorem?
28m
28
45
Answers
A school has 400 students. They all come to school by bus, and each bus carries the same number of students. How many students might there be on each bus?
Answers
Answer:
100 students on each bus
Step-by-step explanation:
100*4 is 400 so there might be just 4
Answer:
Hey there!
It's possible that there are 200 busses, and each bus carries only 2 people, there are 10 busses and each bus carries 40 people, or there are 5 busses and each bus carries 80 people.
Hope this helps :)
An analysis of variance is used to evaluate the mean differences for a research study comparing four treatments with a separate sample of n = 8 in each treatment. If the data produce an F-ratio of F = 4.60, which of the following is the correct statistical decision? a. Reject the null hypothesis with α = .05 but not with α = .01 b. Reject the null hypothesis with either α = .05 or α = .01 c. Fail to reject the null hypothesis with either α = .05 or α = .01 d. There is not enough information to make a statistical decision
Answers
Considering the p-value of the f-ratio, it is found that the correct option is given by:
a. Reject the null hypothesis with α = .05 but not with α = .01.
What is the relation between the p-value and the test hypothesis?Depends on if the p-value is less or more than the significance level:
If it is more, the null hypothesis is not rejected.If it is less, it is rejected.In this problem, the test statistic is of F = 4.60, with 4 x 7 = 28 df between treatments and 7 df in a single treatment, hence, using a calculator, the p-value is of 0.0218, which is less than 0.05 but more than 0.01, meaning that option A is correct.
More can be learned about p-values and hypothesis tests at https://brainly.com/question/26454209
A home buyer is debating between two different mortgages for $167,800. The options are: Option A: 20-year fixed rate loan at 7.45% with a total of $323,198.36 paid in principal and interest over the life of the loan Option B: 15-year fixed rate loan at the same rate. How much more total principal and interest will the buyer pay for the 20-year loan versus the 15-year loan? A spreadsheet was used to calculate the correct answer. Your answer may vary slightly depending on the technology used $46,041.05 $44,061.05 $229,893.95 $292,893.95
Answers
The difference in total principal and interest payment between the 20-year loan versus the 15-year loan is B. $44,061.05.
How is the difference determined?The difference is obtained by computing the total payments for the Option B loan and comparing these to the total payments for Option A loan.
The total payments for Option B can be computed using an online finance calculator that determines also the monthly payments.
Option A:Mortgage loan = $167,800
Interest rate = 7.45%
Mortgage period = 240 (20 years x 12)
Total payment (Future Value) = $323,198.36
Monthly payment = $1,346.66 ($323,198.36/240)
Option B:N (# of periods) = 180 months (15 years x 12)
I/Y (Interest per year) = 7.45%
PV (Present Value) = $167,800
FV (Future Value) = $0
Results:
Monthly Payment (PMT) = $1,550.76
Sum of all periodic payments = $279,137.31
Total Interest = $111,337.31
Option A total payment = $323,198.36
Option B total payment = $279,137.31
Difference between the two options = $44,061.05 ($323,198.36 - $279,137.31)
Learn more about monthly payments at https://brainly.com/question/28106777.
#SPJ1
Let C be the curve of intersection of the cylinder x2+(y−1)2=1 with the plane y=z, traversed in the counterclockwise direction when viewed from the above. Let F(x,y,z)=⟨y2,xy,xz⟩. Use Stokes' theorem to evaluate the line integral ∫CF.dr.
Answers
Stokes' theorem is a fundamental theorem in vector calculus that relates the surface integral of a vector field over a closed surface to the line integral of the vector field around the boundary of that surface.
To evaluate the line integral ∫C F · dr using Stokes' theorem, we need to find the curl of the vector field F and calculate the surface integral of the curl over the surface enclosed by the curve C.
First, let's find the curl of the vector field F(x, y, z) = ⟨y^2, xy, xz⟩:
∇ × F =
| i j k |
| ∂/∂x ∂/∂y ∂/∂z |
| \(y^2\) xy xz |
Expanding the determinant, we have:
∇ × F = (z - y) i + 0 j + (x - 2y) k
Now, let's find the surface enclosed by the curve C, which is the intersection of the cylinder \(x^2 + (y - 1)^2 = 1\) with the plane y = z. This means we have:
\(x^2 + (y - 1)^2 = 1\)
y = z
Substituting y = z into the equation of the cylinder, we get:
\(x^2 + (z - 1)^2 = 1\)
This is the equation of a circle in the x-z plane centered at (0, 1) with a radius of 1.
Next, we need to calculate the surface integral of the curl over this surface. Since the surface is a circle lying in the x-z plane, we can parametrize it as:
r(u) = ⟨r cos(u), 1, r sin(u)⟩
where u is the parameter ranging from 0 to 2π, and r is the radius of the circle (in this case, r = 1).
Now, we can compute dr:
dr = ⟨-r sin(u), 0, r cos(u)⟩ du
Substituting the values into the curl, we have:
∇ × F = (r cos(u) - 1) i + 0 j + (r cos(u) - 2) k
Taking the dot product of F and dr, we get:
F · dr = (\(y^2\))(-r sin(u)) + (xy)(0) + (xz)(r cos(u))
= -r \(y^2\) sin(u) + 0 + r xz cos(u)
= -r(\(1^2\)) sin(u) + 0 + r(r cos(u))(r cos(u) - 2)
= -r sin(u) + \(r^3\)(\(cos^2\)(u) - 2cos(u))
Now, we can integrate this expression over the parameter u from 0 to 2π:
∫C F · dr = ∫₀²π [-r sin(u) + \(r^3\) (\(cos^2\)(u) - 2cos(u))] du
Integrating term by term, we get:
\(\int_C F \cdot dr &= \left[ -r(-\cos u) + \frac{r^3}{3} (\sin u - \sin(2u)) \right]_0^{2\pi} \\&= r(1 - \cos(2\pi)) + \frac{r^3}{3} (\sin(2\pi) - \sin(4\pi)) - \left[ r(1 - \cos(0)) + \frac{r^3}{3} (\sin(0) - \sin(0)) \right] \\&= r(1 + 0) + \frac{r^3}{3} (0 - 0) - \left[ r(1 + 0) + \frac{r^3}{3} (0 - 0) \right] \\&= 0\)
Therefore, the line integral ∫C F · dr evaluates to zero using Stokes' theorem.
To know more about Stokes' theorem visit:
https://brainly.com/question/32515968
#SPJ11
How do i find out if 1/32 is a density property
Answers
Density is how much matter is contained within a volume. A dense object weighs more than a less dense object that is the same size. An object less dense than water will float on it; one with greater density will sink. The density equation is density equals mass per unit volume or D = M / V. (Hope this helped!)
consider the following statement. ∃x ∈ r such that ∀y ∈ r− (the set of negative real numbers), x > y.
Answers
The statement is true. There exists a real number x such that for every real number y that is not negative, x is greater than y.
The statement is expressing the existence of a real number x that is greater than any other real number y, excluding the negative real numbers. In other words, there is at least one positive real number that is larger than any non-negative real number.
To prove this, we can consider x = 1. For any non-negative real number y, we have x = 1 > y. Therefore, the condition of the statement is satisfied, and the statement is true.
In general, this statement reflects the fact that among all the non-negative real numbers, there is always a larger positive real number. This can be visualized on a number line where the positive real numbers extend infinitely to the right, surpassing any non-negative real number.
Learn more about infinitely here: brainly.com/question/32237150
#SPJ11
Plsss help ASAP
200 extra point and brainliest

Answers
Answer:
A, B, D
Step-by-step explanation:
Answer:
A, B, D, E
Step-by-step explanation:
1. 100 = 100%, so seeing that there are 55 boys and 45 girls, we can go ahead and turn those into percentages, making this answer correct.
2. Once again, 100 = 100%, so 17 = 17%
3. "10/55 of those" isn't implying this is the boys only, but rather everyone, so this statement is not correct.
4. 10/35 of the students who chose math are girls. We can see that on the graph.
5. 8 + 8 = 16. Those are both the same number and half and half of the boys and girls...
Hope this helped!
(1 point) rework problem 7 from section 2.3 of your text. assume that the student has a cup with 8 writing implements: 4 pencils, 3 ball point pens, and 1 felt-tip pen. (1) in how many ways can the student select 3 writing implements? 56 equation editorequation editor (2) in how many ways can the selection be made if no more than one ball point pen is selected? equation editorequation editor
Answers
(1)a total of 28 ways the student can select 3 writing implements
2)A total of 25 ways the selection be made if no more than one ballpoint pen is selected.
For the first question, the student has three different types of writing implements and thus three different ways to make a selection. The student can choose any combination of three pencils, three ballpoint pens, or three felt-tip pens. This is known as a combination problem and can be solved using the combination formula. The combination formula, which is often written as "n choose k" (where n is the number of objects and k is the number of objects to be selected), can be used to calculate the total number of possible combinations.
In this case, the student has 4 pencils, 3 ballpoint pens, and 1 felt-tip pen, so the combination formula would be (4 choose 3) + (3 choose 3) + (1 choose 3). This simplifies to 28, meaning that there are 28 possible ways the student can select 3 writing implements.
For the second question, the student is limited to selecting no more than one ballpoint pen. Since the student can only select one ballpoint pen, the combination formula would now be (4 choose 3) + (2 choose 3) + (1 choose 3). This simplifies to 25, meaning that there are 25 possible ways the student can select 3 writing implements without selecting more than one ballpoint pen.
To know more about combination refer to the link brainly.com/question/28720645
#SPJ4
Find two quadratic functions, one that opens upward and one that opens downward, whose graphs have the given x-intercepts. (-5,0), (5,0) opens upward f(x)=x²+x-5 X opens downward f(x)=x²-x+5
Answers
We have found two quadratic functions with x-intercepts (-5,0) and (5,0): f(x) =\(x^2 - 25\), which opens upward, and g(x) = \(-x^2 + 25\), which opens downward.
For the quadratic function that opens upward, we can use the x-intercepts (-5,0) and (5,0) to set up the equation:
f(x) = a(x + 5)(x - 5)
where a is a constant that determines the shape of the parabola. If this function opens upward, then a must be positive. Expanding the equation, we get:
f(x) = a(x^2 - 25)
To determine the value of a, we can use the fact that the coefficient of the x^2 term in a quadratic equation determines the shape of the parabola. Since we want the parabola to open upward, we need the coefficient of x^2 to be positive, so we can set a = 1:
f(x) = x^2 - 25
For the quadratic function that opens downward, we can use the x-intercepts (-5,0) and (5,0) to set up the equation:
g(x) = a(x + 5)(x - 5)
where a is a constant that determines the shape of the parabola. If this function opens downward, then a must be negative. Expanding the equation, we get:
g(x) = a(x^2 - 25)
To determine the value of a, we can use the fact that the coefficient of the x^2 term in a quadratic equation determines the shape of the parabola. Since we want the parabola to open downward, we need the coefficient of x^2 to be negative, so we can set a = -1:
g(x) = -x^2 + 25
For such more questions on quadratic
https://brainly.com/question/1214333
#SPJ8
what are the 2 solutions tot he equation below?

Answers
The solution of the equation are 8 and -8
The equation is b²/4 + 45 =61
b square by four plus forty five equal to sixty one
b is the variable in the equation
We have to find the solution of the equation
b²/4 = 61-45
b²/4 =16
b²=64
b=±8
Hence, the solution of the equation are 8 and -8
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Place the vocabulary words on the diagram to correctly identify the opposite, adjacent, and hypotenuse sides of the
triangle.

Answers
Answer:
LINE QR IS THE HYPOTENUSE
LINE RS IS THE ADJACENT
LINE QS IS THE OPPOSITE.

6 over square root 3
Answers
Sorry if im wrong :)
Jeffrey and Marie just had a baby and want to invest money into a bank account to save money for their newborn. The bank account they are looking into yields 6.8% interest each year. If Jeffrey and Marie invest $500, how much money will be in the account when their child's turns 18 years old
Answers
Answer:
$1,112
Step-by-step explanation:
6.8% x 500= 34
34 x 18 = 612
612 + 500 = 1112
The following data are for an ongoing production decline: - agi=165Mscf/day - Di=0.09/yr - b=0.51 What is the Estimated Ultimate Recovery (EUR) for this reservoir? The units for your answer should be MMscf and your answer should be precise to 0 decimal places: XXXX
Answers
Rounding to 0 decimal places, the Estimated Ultimate Recovery (EUR) for this reservoir is approximately 5,988 MMscf.
To calculate the Estimated Ultimate Recovery (EUR) for the reservoir, we can use the Arps equation, which relates the cumulative production (Q) to time (t) for a declining reservoir:
Q = (b / Di) * ((t + Di)^(-b) - Di^(-b))
Given the following data:
Initial production rate (agi): 165 MMscf/day
Decline rate (Di): 0.09/yr
Hyperbolic exponent (b): 0.51
We want to find the EUR, which is the cumulative production at infinite time (t = ∞).
At infinite time, the Arps equation simplifies to:
EUR = (b / Di) * (Di^(-b))
Substituting the given values into the equation:
EUR = (0.51 / 0.09) * (0.09^(-0.51))
EUR ≈ 5.67 * (1.056)
EUR ≈ 5.98752 MMscf
Rounding to 0 decimal places, the Estimated Ultimate Recovery (EUR) for this reservoir is approximately 5,988 MMscf.
for such more question on Estimated Ultimate Recovery
https://brainly.com/question/3617398
#SPJ8
plssssssssssss help I need to pass

Answers
Answer:
x = 24
Step-by-step explanation:
We can tell by two ways: We already know the value of one of the angles; 66 degrees. We can tell the value of the other one, because it has the right angle symbol, meaning it's 90 degrees. Remember that every triangle's degrees always add up to 180. We can find x by adding 90 and 66 together, which results in 156. Subtract 156 from 180 and you get 24. Therefore, the value of x is 24 degrees.
Answer:
24 degrees
Step-by-step explanation:
The total of a triangle is 180 degrees and a right angle is 90 degrees ( you can tell it's a right angle if it forms the shape of a straight capital "L" or if it has the square in that corner).
So to simplify this , add 90 and 66 which equals 156.
Now we subtract 156 from 180 ----> 180 - 156 = 24
So 24 degrees is your answer.
What is an appropriate display to show the spread of 150 test scores for Mrs. Hansen's last science test?
(ignore my answer, i didn't mean to click it)

Answers
The appropriate display to show the spread of 150 test scores for Mrs. Hansen's last science test is: b. box and whisker plot.
What is box and whisker plot?Box and whisker plot which is also called box plot can be defined as the plot that show a graphical presentation of data set by helping to display the data set or data score .
Hence a graphical presentation display to show the spread of 150 test scores for Mrs. Hansen's last science test is option B which is Box and whisker plot .
Learn more about Box and whisker plot here:https://brainly.com/question/14359396
#SPJ1
Write The recursive formula for the sequence 18,22,26,30?
Answers
The recursive formula is an = a(n-1) +4. A recursive formula is one that defines each term in a sequence by using the term before it (s)
What is recursive formula?A recursive formula is one that defines each term in a sequence by using the term before it (s). The following parameters are defined by the recursive formulas: The sequence's first term. The pattern rule for obtaining any term from its preceding term. A recursive formula is composed of two parts: a statement of the first term and a statement of the formula that connects successive terms. The sequence is as follows: 10, 15, 20, 25, 30, 35,... Look for a recursive formula. This is an arithmetic sequence (the same number, 5, is added to each term to get to the next term).The sequence's first term
The pattern rule for obtaining any term from its preceding term
Recursive Arithmetic Sequence Formula
To find the nth term of an arithmetic sequence, use the recursive formula:
an = an-1 + d for n ≥ 2
Where
an is the nth term of a A.P.
d is the common difference.
Given:
14, 18, 22, 26, 30, …
a1 = 14
and, d = 18-14
d = 4
a2 = a1 + 4
a2 = 14 + 4 = 18
Similarly, going this way
an = a(n-1) +4
Hence, the recursive formula is an = a(n-1) +4
To learn more about recursive formula, refer to:
https://brainly.com/question/27969297
#SPJ13
Write an integer for the situation.
11 mph above the speed limit
PLEASE HELP IM VERY CONFUSED
Answers
Answer:
me
Step-by-step explanation:
A line segment has endpoints at (–4, –6) and (–6, 4). Which reflection will produce an image with endpoints at (4, –6) and (6, 4)? a reflection of the line segment across the x-axis a reflection of the line segment across the y-axis a reflection of the line segment across the line y = x a reflection of the line segment across the line y = –x
Answers
Answer:
reflection in the y- axis
Step-by-step explanation:
Under a reflection in the y- axis
a point (x, y ) → (- x, y )
Note the x- coordinate is opposite in sign and the y- coordinate remains unchanged.
Thus
(- 4, - 6 ) → (4, - 6 )
(- 6, 4 ) → (6, 4 )
The endpoints have been reflected in the y- axis
We want to see which reflection we need to use to transform the given segment into the desired one.
The correct answer is:
"a reflection of the line segment across the y-axis"
First, we want to change the segment with endpoints at (-4, -6) and (-6, 4) to a segment with endpoints (4, -6) and (6, 4).
Note that the only thing that changes is the x-value of the endpoints, so we need to apply a reflection that only changes the x-value.
That reflection is a reflection across the y-axis.
For a general point (x, y), a reflection across the y-axis transforms the point to (-x, y).
Then the correct option is:
"a reflection of the line segment across the y-axis"
If you want to learn more, you can read:
https://brainly.com/question/15476267
The sales tax rate in connecticut is 6. 35%. Megan wants to buy a jacket with a $45 price tag. She has a gift card to the store she wants to use. What amount needs to be on the gift card for Megan to be able to buy the jacket using only the gift card?
Answers
Megan needs a gift card with a minimal cost of $47.86 to be able to buy the jacket using simplest the gift card.
Assuming the gift card covers the total cost of the jacket, the amount at the present card that Megan needs to buy the jacket may be calculated as follows:
Jacket rate = $45
sales tax price in Connecticut = 6.35%
Tax amount = $45 x 6.35% = $2.86
total value of the jacket which includes tax = $45 + $2.86 = $47.86
Consequently, For a minimum cost of $47.86, Megan will need a gift card in order to buy the jacket with just the gift card.
Learn more about sales tax:-
https://brainly.com/question/30109497
#SPJ4
Please help!! 50 points!!
Use the exponential equation below to answer Part A, Part B, and Part C.
35^x = 8
Part A: Explain the steps to solve the equation.
Part B: Rewrite the exponential equation in logarithmic form using the definition of logarithms.
Part C: Use the equation from Part B to solve for x. Round to the nearest hundredth
Answers
Answer:
a) below
b) log_35 (8) = x
c) x = 0.58487
Step-by-step explanation:
a) 35^x=8
apply the exponent rule
xln(35) = ln(8) → x = ln(8)/ln(35) → x = 3ln(2)/ln(35)
x = 0.58487
c) log_35 (8) = x
x = log_35 (8)
base form (Rewrite 8 in power)
x = log_35 (2^3)
log rule: log_a(x^b) = b*log_a(x)
log_35 (2^3) = 3log_35(2)
x = 3log_35(2)
x = 0.58487