form the equation: maha's father is 46 years old. He is 6 years older than four times maha's age. (let maha's age be x)
Answers
Related Questions
Identify the sample space of the probability experiment and determine the number of outcomes in the sample space Randomly choosing an even number between 1 and 10, inclusive
The sample space is______. (Use a comma to separate answers as needed. Use ascending order) There are________outcome(s) in the sample space.
Answers
Answer:
Step-by-step explanation:
Sample Space
off even numbers
= {2,4,6,8,10}.
There are 5 outcomes in the sample space,
PLEASE HELP ME!!!!
The equation of a parabola is given.
y=1/8x2+4x+20
What are the coordinates of the focus of the parabola?
Enter your answer in the boxes.
Answers
Answer:
The focus would lie at (-8,16)
Step-by-step explanation:
What is the value of 7P3?
021
35
210
840
Answers
Answer:
210
Step-by-step explanation:
The answer for 7p3 is : 210. This can be solved in the following way: 7p3 is an expression for permutation which means the number of ways of arranging 3 items from a total of 7 items.
Hope This Help?
Please Mark Me Brainly!
Diego is solving the equation x^2-12x = 21
Answers
Answer:
The solutions to the quadratic equations will be:
\(x=\sqrt{57}+6,\:x=-\sqrt{57}+6\)
Step-by-step explanation:
Given the expression
\(x^2-12x\:=\:21\)
Let us solve the equation by completing the square
\(x^2-12x\:=\:21\)
Add (-6)² to both sides
\(x^2-12x+\left(-6\right)^2=21+\left(-6\right)^2\)
simplify
\(x^2-12x+\left(-6\right)^2=57\)
Apply perfect square formula: (a-b)² = a²-2ab+b²
i.e.
\(x^2-12x+\left(-6\right)^2=\left(x-6\right)^2\)
so the expression becomes
\(\left(x-6\right)^2=57\)
\(\mathrm{For\:}f^2\left(x\right)=a\mathrm{\:the\:solutions\:are\:}f\left(x\right)=\sqrt{a},\:-\sqrt{a}\)
solve
\(x-6=\sqrt{57}\)
add 6 to both sides
\(x-6+6=\sqrt{57}+6\)
Simplify
\(x=\sqrt{57}+6\)
also solving
\(x-6=-\sqrt{57}\)
add 6 to both sides
\(x-6+6=-\sqrt{57}+6\)
Simplify
\(x=-\sqrt{57}+6\)
Therefore, the solutions to the quadratic equation will be:
\(x=\sqrt{57}+6,\:x=-\sqrt{57}+6\)
I’ll give thanks, 5 stars and brainliest
Continue the pattern till the tenth digit. 1, 4, 9, 16,...
Answers
Answer:
25,36,49,64,81,100
................................
Answer:
Your answer is 1, 4, 9, 16, 25, 36, 49, 64, 81, 100.
Step-by-step explanation:
1 - 4
+ 3
4 - 9
+ 5
9 - 16
+ 7
+9, +11, +13, +15, +17, +19...
Factor this polynomial expression, and wrote it in its fully factored form 3x^3 + 3x^2 - 18x

Answers
Answer:
fourth option
Step-by-step explanation:
Given
3x³ + 3x² - 18x ← factor out 3x from each term
= 3x(x² + x - 6) ← factor the quadratic
Consider the factors of the constant term (- 6) which sum to give the coefficient of the x- term (+ 1)
The factors are + 3 and - 2, since
3 × - 2 = - 6 and 3 - 2 = + 1, thus
x² + x - 6 = (x + 3)(x - 2) and
3x³ + 3x² - 18x = 3x(x + 3)(x - 2) ← in factored form
When you design an algorithm, it should be general enough to provide a solution to many problem instances, not just one or a few of them.T/F?
Answers
It is true that when you design an algorithm, it should be general enough to provide a solution to many problem instances, not just one or a few of them.
In mathematics, an algorithm is a process, a description of a series of steps that may be used to solve a problem; however, they are now far more prevalent than that.
Although many areas of research (and daily life) employ algorithms, long division's step-by-step process is probably the most prevalent example.
Thus, It is true that when you design an algorithm, it should be general enough to provide a solution to many problem instances, not just one or a few of them.
To know more about algorithm visit: brainly.com/question/29289479
#SPJ4
What is the equation of this line?
A: y=-2x
B: y = ½x
C: y = -½x
D: y = 2x

Answers
Answer:
D
Step-by-step explanation:
when x=1, y should = 2
2(1)=2
so y=2x is correct
In the lecture, we show the v-structure X→Z←Y, where X happening decreases the probability of Y happening. Examples include E→J←A and medical diagnosis. Show that for a v-structure X→Z←Y with some parametrization, the occurrence of X may increase the probability of Y happening given Z.
Answers
The parametrization occurrence of X (studying) increases the probability of Y (performing well on the exam) happening given Z (knowledge) in the v-structure X → Z ← Y.
In a v-structure X → Z ← Y, the occurrence of X indeed increase the probability of Y happening given Z, depending on the parametrization of the variables.
To illustrate this, let's consider a different example:
Suppose the v-structure X → Z ← Y, where X represents a student studying for an exam, Z represents the student's knowledge, and Y represents the student's performance on the exam.
Assume the following parametrization:
If the student studies (X = 1), their knowledge (Z) improves, increasing the probability of performing well on the exam (Y = 1).
If the student does not study (X = 0), their knowledge (Z) does not improve, decreasing the probability of performing well on the exam (Y = 1).
In this parametrization, that the occurrence of X (studying) increases the probability of Y (performing well on the exam) happening given Z (knowledge). When the student studies (X = 1), their knowledge (Z) improves, leading to a higher chance of performing well on the exam (Y = 1). Conversely, if the student does not study (X = 0), their knowledge (Z) does not improve, reducing the probability of performing well on the exam (Y = 1).
To know more about probability here
https://brainly.com/question/31828911
#SPJ4
find the values of the variables in the matrix calculator
Answers
Double-check the input and review the solution provided by the matrix calculator to ensure accuracy.
The matrix calculator is a useful tool for solving equations involving matrices. To find the values of the variables in the matrix calculator, follow these steps:
1. Enter the coefficients of the variables and the constant terms into the calculator. For example, if you have the equation 2x + 3y = 10, enter the coefficients 2 and 3, and the constant term 10.
2. Select the appropriate operations for solving the equation. The calculator will provide options such as Gaussian elimination, inverse matrix, or Cramer's rule. Choose the method that suits your equation.
3. Perform the selected operation to solve the equation. The calculator will display the values of the variables based on the solution method. For instance, Gaussian elimination will show the values of x and y.
4. Check the solution for consistency. Substitute the obtained values back into the original equation to ensure they satisfy the equation. If they do, you have found the correct values of the variables.Remember to double-check the input and review the solution provided by the matrix calculator to ensure accuracy.
Learn more about Matrix here,https://brainly.com/question/27929071
#SPJ11
help plzzzzzz as soon as possible

Answers
Answer:
when x = -5 y is -48
when x is -1 y is -8
when x is 0 y is 2
when x is 1 y is 12
Step-by-step explanation:
PLEASE SOMEONE HELP ME
Question 2 (6 points)
Jonny is writing a program for a video game.
For one part of the game he uses the
rule given below to move objects on the screen.
Showing all your work, give the output that the rule gives for the inputs.
(x, y) + (2 – 7.5, y + 6.8)
First input: (4.4.2.5)
Second input: (9.7, -2.9)
Answers
Answer:
.
Step-by-step explanation:
Answer:
(-3.2 , 12.3)
(0.7 , 3.6)
Step-by-step explanation:
The rule :
(x, y)→(x−7.5, y+6.8)
For the x - coordinate ; Subtract 7.5
For the y - coordinate `; add 6.8
First input : (4.3, 5.5)
Output :
x = 4.3 - 7.5 = - 3.2
y = 5.5 + 6.8 = 12.3
Output = (4.3, 5.5) →(-3.2 , 12.3)
Second input : (8.2, -3.2)
Output :
x = 8.2 - 7.5 = 0.7
y = - 3.2 + 6.8 = 3.6
Output = (8.2, -3.2)→(0.7 , 3.6)
The outputs obtained are :
(-3.2 , 12.3) and (0.7 , 3.6)
the cost of a school banquet is $95 plus $15 for each person attending. Write an equation that gives total cost as a function of the number of people attending. What is the cost for 77 people?
Answers
Answer:
equation: y=15x+95
it would cost $1250
Answer:
f(x) = 95 + 15x
Cost for 77 people = $1250
Step-by-step explanation:
15 x 77 = 1155
1155 + 95 = 1250
Isolating a variable in two equations is easiest when one of them has a coefficient of 1. Let's say we have the two equations 3A-B 5 and want to isolate one of the variables, such that it appears by itself on one side of the equation. Which of the following is an equation with one of the above variables isolated? View Available Hint(s) B=3A-5 2A-3B- 4 Submit
Answers
The equation that isolates one of the variables is:
B =3A-5
To isolate one of the variables, we need to rearrange the equations so that the variable appears by itself on one side of the equation.
In the given equations:
1) 3A - B = 5
2) 2A - 3B = -4
To isolate variable B, we can start with equation 1 and add B to both sides:
3A - B + B = 5 + B
Simplifying, we have:
3A = 5 + B
Similarly, to isolate variable A, we can start with equation 2 and subtract 2A from both sides:
2A - 3B - 2A = -4 - 2A
Simplifying, we have:
-3B = -4 - 2A
Thus, the equation that isolates variable B is B = 3A-5. This equation allows us to express B solely in terms of A, with the variable B appearing alone on one side.
learn more about variable here:
https://brainly.com/question/14561515
#SPJ4
the complete question is:
Which of the following equations isolates one of the variables (A or B) from the given system of equations:
1) 3A - B = 5
2) 2A + 3B = -4
a) 3B = -2A - 4
b) B = 5 - 3A
c) B = 3A - 5
d) 2A = -3B - 4
Which equation, among the options a) to d), expresses one of the variables (A or B) by itself on one side of the equation, following the guideline that isolating a variable is easiest when one of the equations has a coefficient of 1 for that variable?
5. Find the measure of arc AC.
Find mAC
A) 52
B) 72
C) 92
D) 112

Answers
Answer:
B: 72
Step-by-step explanation:
Here, we want to find the measure of arc AC
Mathematically, we will use an angle arc relationship here
The angle arc relationship to use here is that the arc AC is twice the measure of angle ABC
Thus, we have the arc AC as 2 * 36 = 72 degrees
A Boy Scout troop is selling Christmas trees at a local tree lot in the morning they sold 11 Douglas fir trees and nine noble fir trees turning a total of $1006 in the afternoon they sold 14 Douglas fir trees and nine noble fir trees turning a total of $1111 how much do the Douglasfir trees cost
Answers
Answer:
$35
Step-by-step explanation:
Let x represent the price of Douglas fir trees and y represent the noble fir trees
11x + 9y= 1006........equation 1
14x + 9y= 1111.........equation 2
Multiply equation 1 by 14 and equation 2 by 11
154x + 126y= 14,084
-
154x + 99 y= 12,221
27y= 1863
Divide both sides by the coefficient of y which is 27
27y/27 = 1863/27
y= 69
Substitute 69 for y in equation 1
11x + 9y= 1006
11x + 9(69) = 1006
11x + 621= 1006
11x = 1006 -621
11x = 385
x = 385/11
x = 35
Hence the Douglas fir free costs $35
Estimate ∫10cos(x2)dx∫01cos using (a) the Trapezoidal Rule and (b) the Midpoint Rule, each with n=4. Give each answer correct to five decimal places.
(a) T4=
(b) M4=
(c) By looking at a sketch of the graph of the integrand, determine for each estimate whether it overestimates, underestimates, or is the exact area.
Underestimate Overestimate Exact 1. M4
Underestimate Overestimate Exact 2. T4
(d) What can you conclude about the true value of the integral?
A. T4<∫10cos(x2)dx
B. T4>∫10cos(x2)dxand M4>∫10cos(x2)dx
C. M4<∫10cos(x2)dx
D. No conclusions can be drawn.
E. T4<∫10cos(x2)dx and M4<∫10cos(x2)dx
Answers
a)Using the Trapezoidal Rule with n=4: T4 = 1.06450
b)Using the Midpoint Rule with n=4: M4 = 1.14750
c)M4 overestimates the area while T4 underestimates the area
d) The true value of the integral is T4<∫10cos(x2)dx and M4<∫10cos(x2)dx
What is Trapezoidal Rule?
The Trapezoidal Rule is a numerical integration method that approximates the area under a curve by approximating it with a series of trapezoids and summing their areas.
According to the given information:
(a) Using the Trapezoidal Rule with n=4:
Δx = (1-0)/4 = 0.25
f(0) = cos(0) = 1
f(0.25) = cos(0.0625) ≈ 0.998
f(0.5) = cos(0.25) ≈ 0.968
f(0.75) = cos(0.5625) ≈ 0.829
f(1) = cos(1) ≈ 0.540
T4 = Δx/2 * [f(0) + 2f(0.25) + 2f(0.5) + 2f(0.75) + f(1)]
≈ 0.25/2 * [1 + 2(0.998) + 2(0.968) + 2(0.829) + 0.540]
≈ 1.06450
(b) Using the Midpoint Rule with n=4:
Δx = (1-0)/4 = 0.25
x1 = 0 + Δx/2 = 0.125
x2 = 0.125 + Δx = 0.375
x3 = 0.375 + Δx = 0.625
x4 = 0.625 + Δx = 0.875
f(x1) = cos(0.015625) ≈ 0.999
f(x2) = cos(0.140625) ≈ 0.985
f(x3) = cos(0.390625) ≈ 0.921
f(x4) = cos(0.765625) ≈ 0.685
M4 = Δx * [f(x1) + f(x2) + f(x3) + f(x4)]
≈ 0.25 * [0.999 + 0.985 + 0.921 + 0.685]
≈ 1.14750
(c) Looking at a sketch of the graph of the integrand, it appears that the function is decreasing on the interval [0,1], so the area under the curve should be decreasing. The Midpoint Rule tends to overestimate the area under a decreasing curve, while the Trapezoidal Rule tends to underestimate it. Therefore, the answers are:
M4 overestimates the area
T4 underestimates the area
(d) We can conclude that the true value of the integral is between the estimates given by the Trapezoidal Rule and the Midpoint Rule, since the Trapezoidal Rule underestimates and the Midpoint Rule overestimates. Therefore, we can say:
E. T4<∫10cos(x2)dx and M4<∫10cos(x2)dx
To know more about Trapezoidal Rule visit:
https://brainly.com/question/31494228
#SPJ1
PLEASE HELP! I WILL GIVE BRAINLIEST!

Answers
Answer:
it would be 9/8 as the perimeter
Step-by-step explanation:
you would add all the sides together
1/8+3/4+1/4 = 9/8
Answer:
1 1/8 in.
Step-by-step explanation:
you have to add up all of the sides. 3/4 plus 1/4 equals 1. 1 plus 1/8 equals 1 1/8. Hope I helped you : )
A rectangular carpet has a perimeter of 16m and area 15 m^2. Find the lengths of the carpets sides
Answers
While guessing and checking is one way to do this problem, I will show you how to do it algebraically.
Let one side be A
Let the other side be B
2(A+B)=16
A*B=15
First equation because the perimeter is 16 and the second because the area is 15. Now solve the system of equations
A+B=8
A=8-B
Substitute into equation two
B(8-B)=15
-B^2+8b-15=0
B^2-8b+15=0
(B+3)(B+5)=0
B=3,5
A=5,3 respectively
From this we can see that one side is 5 meters long while the other side is three meters long.
Step-by-step explanation
Since we're looking at a rectangle, let's consider its perimeter and area formulas.
Perimeter: 2x + 2y (A rectangle has four sides, with two equal sides, so this is x + x + y + y simplified)
Area: (x)(y) (length x breadth so, x times y)
So we have two equations: 2x + 2y = 16 and x*y = 15. Solve simultaneously. Refer to the attached image.
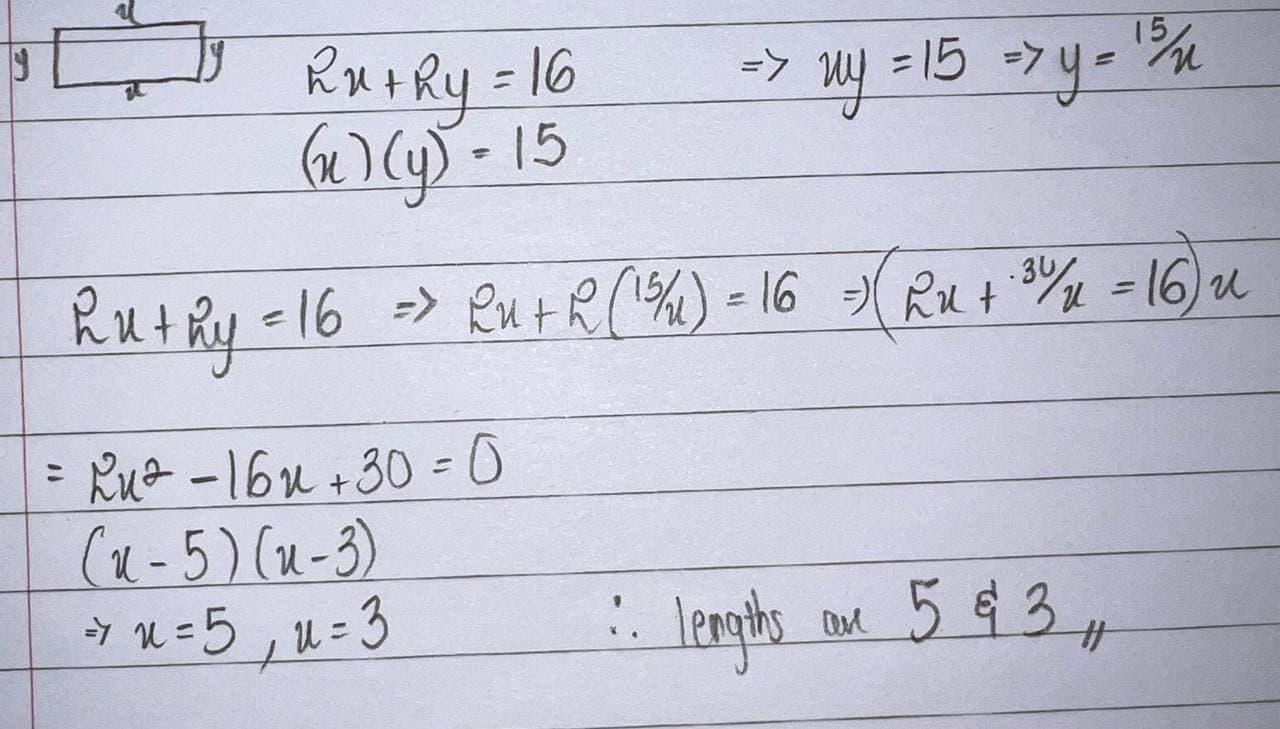
What value of [S] as a fraction of KM, is required to obtain 20% Vmax? [S] equals: a. 0.2 KM b. 0.25 KM c. 0.5 KM d. 0.75 KM e. 0.8.
Answers
The fraction of KM that is required to obtain 20% Vmax is [S] = 0.2 KM.
The Michaelis-Menten equation is given by: V = Vmax[S] / (KM + [S])where, V is the velocity of the reaction, Vmax is the maximum velocity of the reaction,[S] is the substrate concentration, and KM is the Michaelis constant of the enzyme.
Substituting V = 0.2V
max and rearranging the equation,
0.2Vmax = Vmax[S] / (KM + [S])
Multiplying both sides by
(KM + [S]),0.2V
max(KM + [S]) = Vmax[S]
Expanding the equation,
0.2VmaxKM + 0.2Vmax[S]
= Vmax[S]0.2VmaxKM
= 0.8Vmax[S]
Dividing both sides by
Vmax,0.2KM = 0.8[S]
Simplifying the equation,
[S] = 0.2 KM / 0.8[S] = 0.25 KM
Therefore, the fraction of KM that is required to obtain 20% Vmax is [S] = 0.2 KM, which is option (a).
Learn more about velocity from:
https://brainly.com/question/80295
#SPJ11
Simplify the following Boolean function using Boolean Algebra rule. F = xy'z' + xy'z + w'xy + w'x'y' + w'xy
Answers
When the above is simplified using Boolean Algebra, we have F = x' + y' + w'xy.
What is the explanation for the above ?
We can simplify the Boolean function F = xy'z' + xy'z+ w'xy + w'x'y' + w'xy using the following Boolean Algebra rules.
Absorption - x + xy = x
Commutativity - xy = yx
Associativity - x(yz) = (xy)z
Distributivity - x(y + z) = xy + xz
Using the above , we have
F = xy'z' + xy'z+ w'xy + w'x'y' + w'xy
= xy'(z + z') + w'xy(x + x')
= xy' + w'xy
= (x' + y)(x' + y') + w'xy
= x' + y' + w'xy
This means that the simplified expression is F = x' + y' + w'xy.
Learn more about Boolean Algebra:
https://brainly.com/question/31647098
#SPJ4
please answer with clear instructions so that i can apply this to other questions

Answers
Answer:
Hope it will help you a lot.

Factor the GCF out of each term of the polynomial.

Answers
Answer For The Number 22: Factors of 22 are 1, 2, 11, 22. There are 4 integers that are factors of 22. The greatest factor of 22 is 22. 3.
Answer For The Problem 2x3 (Divide it by the numbers I give you meaning divide the number two by what I give yo and the other number 3 by it.
The common factors for 2,3 are −1,1 . The numbers do not contain any common variable factors. The GCF (HCF) of the numerical factors −1,1 is 1 .The number is one.
Answer For The Problem 2x5 is also 1 so decide both 2&5 by 1 then multiply. After doing that for answers 2&3 add them. last if you then subtract 22 that might be the answer so put that & also put the answer of the greatest common factor of 22 which is 3. Make sure to include that the one where you subtracted 3 was the greatest common factor for 22.
how many different spanning trees does each of these simple graphs have? a) k3 b) k4 c) k2,2 d) c5
Answers
The number of different spanning trees for each graph is: a) K3: 1, b) K4: 4, c) K2,2: 2 and d) C5: 5.
a) The complete graph K3 consists of 3 vertices, and in a spanning tree, we need to have exactly 3 vertices connected without forming any cycles. Therefore, K3 has only one possible spanning tree.
b) The complete graph K4 has 4 vertices. To form a spanning tree, we need to connect all 4 vertices without creating any cycles. K4 can be thought of as a tree with 4 branches extending from a central vertex. Each branch can be connected to any of the other vertices. Hence, there are 4 possible spanning trees for K4.
c) The complete bipartite graph K2,2 consists of 4 vertices divided into two sets, each containing 2 vertices. To form a spanning tree, we need to connect all 4 vertices without creating any cycles. Since there are only two possible edges between the two sets, there are only two possible spanning trees for K2,2.
d) The cycle graph C5 consists of 5 vertices arranged in a circular shape. To form a spanning tree, we need to connect all 5 vertices without creating any cycles. Removing any one of the edges from the cycle will result in a tree. Therefore, C5 has 5 different spanning trees.
Therefore, the number of different spanning trees for each graph is:
a) K3: 1
b) K4: 4
c) K2,2: 2
d) C5: 5
To learn more about spanning trees from the given link
https://brainly.com/question/29998496
#SPJ4
What transformation is happening

Answers
Answer:
Probably c: f(x) = y + 3
Step-by-step explanation:
See attached worksheet

Which is an equation in point-slope form for the given point and slope? point: (–3, 7); slope: 4
Answers
The equation of line that passes a point (–3, 7) and has slope of 4, in the point-slope form is y - 7 = 4 (x + 3)
A linear equation can be expressed in three forms:
- slope intercept form : y = mx + c
- point-slope form: y - y₁ = m (x - x₁)
- standard form: Ax + By + C = 0
Where:
m = slope
(x₁, y₁) = point on the line
A, B, C are constant
In this problem, the point is (–3, 7) and the slope is 4. Hence,
x₁ = –3
y₁ = 7
m = 4
Plug these parameters into the equation:
y - y₁ = m (x - x₁)
y - 7 = 4 (x - (-3))
y - 7 = 4 (x + 3)
Learn more about point-slope form here:
https://brainly.com/question/24907633
#SPJ4
Answer the question Below.

Answers
Answer:
BX = 7 inches
Step-by-step explanation:
Since ABCD is a rectangle, the diagonals are equal and bisect each other
⇒ AC = BD and
AX = CX = BX = DX = AC/2 = BD/2
⇒ BX = A/2
⇒ BX = 14/2
⇒ BX = 7
Sixteen added to a number is equal to forty. Find the number.
Answers
Answer:
The number is 24
Step-by-step explanation:
Let x = number
Add 16 to the number
x+16
Is equal to 40
x+16 = 40
Subtract 16 from each side
x+16-16 = 40-16
x = 24
find the slope (0,-4) and (-6,-2)
Answers
m= (-4-(-2))/(-6–0)
m= -2/-6
m= 1/3
The slope is 1/3
A stackable CD rack holds 20 CDs and costs $3. Mark has a collection of 120 CDs. How much will it cost him to buy enough racks to hold all of his CDs?
Answers
Answer:
You would need $18 total to buy the racks needed.
Step-by-step explanation:
First, every 20 CDs needs a new rack, so you would divide 120 by 20.
120 / 20 = 6 racks
Second, you would multiply the price ($3) of a rack by how many racks needed.
3 * 6 = $18