For the given table of values for a polynomial function, where must the zeros of the function lie?
A. between 2.0 and 2.5 and between 4.0 and 4.5
B. between 2.5 and 3.0 and between 4.0 and 4.5
C. between 2.0 and 2.5 and between 3.5 and 4.0
D. between 2.5 and 3.0 and between 3.5 and 4.0

Answers
Answer:
(B). between 2.5 and 3.0 and between 4.0 and 4.5.
Step-by-step explanation:
According to the Question,
If the value of the function is 0 at x=c, then c is a root or zero of the function. It means the graph of function intersects the x-axis at its zeroes.From the given table it is clear that the value of function are
x | f(x) | Sign
2.0 | 2.8 | Positive
2.5 | 1.1 | Positive
3.0 | –0.8 | Negative
3.5 | –1.2 | Negative
4.0 | –0.3 | Negative
4.5 | 0.7 | Positive
The sign of values of function changes in interval 2.5-3.0 and 4.0-4.5. It means the graph of function must intersect the x-axis in intervals 2.5-3.0 and 4.0-4.5. So, the zeros of the function lie between 2.5 and 3.0 and between 4.0 and 4.5.Therefore, the correct option is B.
Related Questions
Mr. Brown wants to place a water heater that has a volume of 100 liters and a diameter of 40 cm into a strong-box. Will the water heater fit in the strong-box if it has a width of 45 cm and a height of 90 cm? Use П as 3.14.
Answers
Yes, the room heater will fit into the robust box, which is 45 cm in width and 90 cm in height.
what is cylinder ?The cylindrical, which is frequently a lobed solid, comprises one of the most simple curvature geometric forms. In simple geometry, it is known as a prism with a circle as its basis. The term "cylinders" is also used to refer to an infinitely curved surface in a number of modern domains of topology and geometries. A "cylinder" is a two half object made up of curved surfaces with circle tops and bases. A cylinder is a two half solid figure with two bases that are both similar circles connected at its height, which is controlled by the separation of the legs from the center. Cans of iced drinks and the wicks from toilet paper are example of cylinders.
given
r = d/2 = 40/2 = 20 cm
v = pi *r*r*h
100 = 3.14 * 20*20 *h
100 = 1256*h
h = 0.08 cm
strong box = surface area of cuboid = 45 * 90
= 4050 cm2
surface area of water heater = A=2πrh+2πr2=2·π·20·0.08+2·π·202
≈2523.3
Yes, the room heater will fit into the robust box, which is 45 cm in width and 90 cm in height.
To know more about cylinder visit:
https://brainly.com/question/16134180
#SPJ1
matrix diagrams show optionality and cardinality of the erds they document. true or false?
Answers
Matrix diagrams show optionality and cardinality of the erds they document is a false statement.
Matrix diagrams are graphical representations that display the relationships between two or more sets of items. They are commonly used in various fields, including project management, decision-making, and process improvement.
While matrix diagrams can be used to depict relationships and interactions between different elements, such as processes, functions, or components, they do not specifically show optionality and cardinality as defined in Entity-Relationship Diagrams (ERDs).
Optionality and cardinality are concepts typically associated with ERDs, which are used in database design to illustrate the relationships between entities. Optionality refers to the participation or existence of entities in a relationship (e.g., mandatory or optional participation), while cardinality specifies the number of instances of one entity that can be associated with another entity [e.g., one-to-one, one-to-many, many-to-many relationships].
Matrix diagrams, on the other hand, are not specifically designed to represent these concepts and focus more on visualizing the relationships between items rather than expressing optionality and cardinality.
Learn more about matrix here, https://brainly.com/question/11989522
#SPJ11
A cylinder has a radius of 3.2 meters its volume is 190 Cubic meters find its height to the nearest 10th of a meter
Answers
Answer:
volume = pi r^2 h
or, 190 = pi (3.2)^2 h
or, 190/10.24 = pi h
or, 18.56 = 22/7 h
or, 18.56×7/22 = h
thus , h = 5.9037
calculate the customer lifetime value (clv) for a credit card product with a 100k sign-on bonus offer and $450 annual fee for the following three sub-segments: transactors, revolvers and dormants.
Answers
The CLV for transactors is $37.5, for revolvers it is $208.33, and for dormants, it is $2,000,000.
Customer Lifetime Value (CLV) is a financial analysis of the total revenue an organization can reasonably anticipate from a single customer over the course of their relationship. It is the net present value of the cash flows attributed to the relationship with a customer.
This metric is widely used in business to determine how valuable a customer is to the company.
The formula for CLV is:
CLV = (Average Value of a Sale) X (Number of Repeat Transactions) X (Average Retention Time in Months or Years)
There are three sub-segments of the credit card product: transactors, revolvers, and dormants.
The transactors are customers who pay off their credit card balance every month.
Revolvers are customers who carry a balance from month to month.
Dormants are customers who no longer use their credit card.
Each sub-segment will have a different CLV.
Here is how to calculate CLV for each sub-segment:
Transactors:
CLV = (Annual Fee) X (1/Churn Rate)
CLV = (450) X (1/12)
CLV = 37.5 dollars
Revolvers:
CLV = (Annual Interest Paid) X (Average Customer Lifespan)
CLV = (5000) X (1/24)
CLV = 208.33 dollars
Dormants:
CLV = (Number of Dormant Customers) X (Average Annual Spend per Customer) X (Profit Margin)
CLV = (10,000) X (1000) X (0.2)
CLV = 2,000,000 dollars
Therefore, the CLV for transactors is $37.5, for revolvers it is $208.33, and for dormants, it is $2,000,000.
Learn more about the customer lifetime value from the given link-
https://brainly.com/question/28539902
#SPJ11
Find a particular solution of the following differential equations:
(a) y" + 3y + 2y = –20 sin(2x)
(b) y" – 4y + 13y = 2e21 [(1 + 6x) cos(3x) + (12.x – 8) sin(3x)]
Answers
The value of Differential Equation will be \(y_1=c_1 e^{-x}+c_2 e^{-2 x}+\sin (2 x)+3 \cos (2 x)\)
\($$\begin{aligned}& y^{\prime \prime}+3 y^{\prime}+2 y=-20 \sin (2 x) \\& \frac{d^2}{d x^2} y+3 \frac{d}{d x} y+2 y=-20 \sin (2 x)\end{aligned}$$\)
A second order linear, non-homogeneous ODE has the form of ay"+b y'+cy=g(x).
General Solution can be written as y=y_h+y_p y_h is the solution to the homogenous ODE
a(x) y"+b(x) y'+c(x) y=0
Y_p is the particular solution to any function that Satisfies the non-homogenous equation.
Finding. y_n by solving
\(\frac{d^2}{d x^2}(y)+3 \frac{d}{d x}(y)+2 y=0 . \quad y=e^{y-t} .\)
We can rewrite it as:
\(\frac{d^2}{d x^2}\left(\left(e^{x x}\right)\right)+3 \frac{d}{d x}\left(e^{y x}\right)+2 e^{y x}=0 \quad y=e^{y x}\)
We will get it after solving as:
\($\frac{d^2}{d x^2}\left(e^{8 x}\right)$\) apply for chain role
we get \($\Rightarrow r^2 e^{r x}$\)
\($$\begin{aligned}& \quad \frac{d}{d x}\left(e^{r x}\right) \Rightarrow \text { we get }=e^{r x} r \text { sob } \\& \therefore \quad r^2 e^{r x}+3 e^{r x} r+2 e^{r x}=0 .\end{aligned}$$\)
Factor \($e^{r x}\left(r^2+3 y+2\right)=0$\)
By solving this we get r=-1, fr=-2
For two real roots \($r_1 \neq r_2$\).
The general solution will be:
\($$y=c_1 e_2^{-x}+c_2 e^{-2 x}$$\)
Similarly, further solving, we wll get: \(\frac{d^2}{d x}(y)+3 \frac{d}{d x}(y)+2 y=-20 \sin (2 x)\)
We will get it as:
y=sin (2 x)+3 cos (2 x)
\(y_1=c_1 e^{-x}+c_2 e^{-2 x}+\sin (2 x)+3 \cos (2 x)\)
For more questions on Differential Equation
https://brainly.com/question/19130837
#SPJ4
The correct question should be:
Find a particular solution of the following differential equations:
y" + 3y + 2y = –20 sin(2x)
Point P' is the image of P (-2, 4) under a translation by 2 units to the left and 5 units down. What are the coordinates of P'? Please answer within this hour i really need this
Answers
Answer:
(-4, -1)
Step-by-step explanation:
"A translation by 2 units to the left and 5 units down" would be: \((x,y)\rightarrow(x-2,y-5)\)
Apply the rule to point P:
\((-2,4)\rightarrow(-2-2,4-5)\rightarrow\boxed{(-4,-1)}\)
P' should be be (-4, -1).
Hope this helps.
The required points after the translation of P (-2, 4) under a translation by 2 units to the left and 5 units down is P'(-4, -1).
Point P' is the image of P (-2, 4) under a translation by 2 units to the left and 5 units down. What are the coordinates of P' is to be determined.
What is simplification?The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
Here,
P (-2, 4)
under a translation by 2 units to the left and 5 units down.
P becomes P'
Coordinate of the P' = (-2 - 2 , 4 - 5)
= (-4, -1)
Thus, the required points after the translation of P (-2, 4) under a translation by 2 units to the left and 5 units down is P'(-4, -1).
Learn more about simplification here:
https://brainly.com/question/12501526
#SPJ2
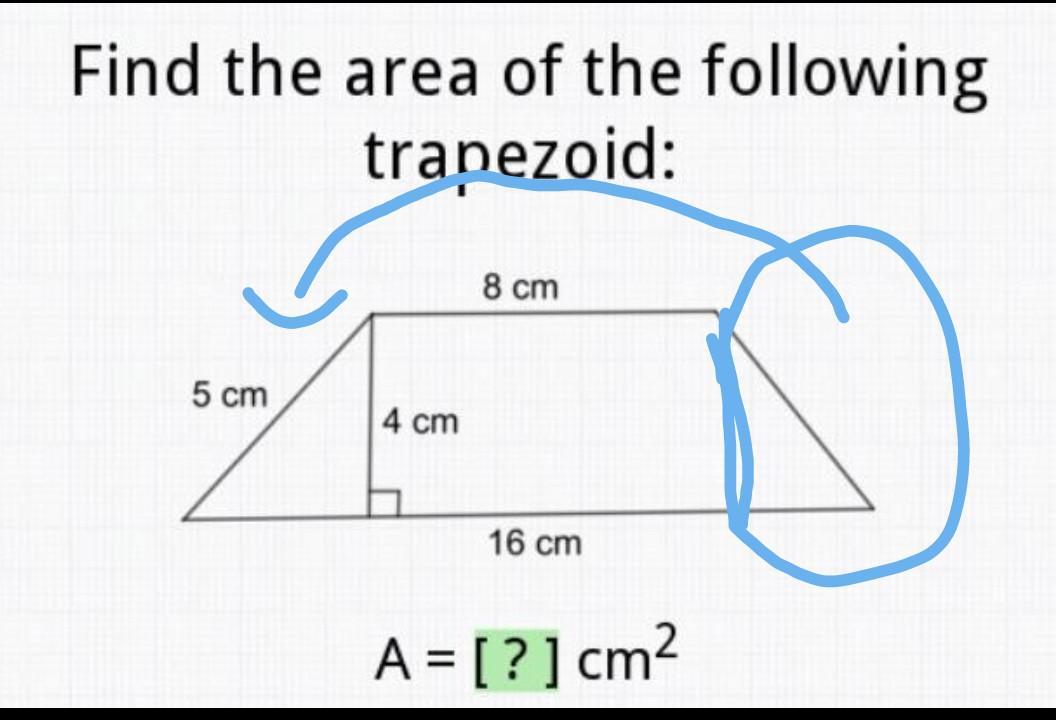
Find the area of the following trapezoid.

Answers
Answer:
Your answer should be 48 \(cm^{2}\).
Step-by-step explanation:
Hope this helps!
Answer:
48 cm square
Step-by-step explanation:
12×4=48
explanation attached

what is square of 2x-3 help me
Answers
Answer:
4x² - 12x + 9
Step-by-step explanation:
Use the foil method.
(2x - 3) (2x - 3)
= 4x²- 6x - 6x + 9
= 4x² - 12x + 9
Answer:
\(Square \ of \ (2x - 3) = 4x^2 - 12x + 9\)
Step-by-step explanation:
\((a +b)^2 = a^2 + b^2 + 2ab\)
\((2x + (- 3))^2 = (2x)^2 + ( -3 )^2 + ( 2\times 2x \times - 3)\\\\\)
\(= 4x^2 + 9 + ( -12x)\\\\=4x^2 - 12 x + 9\)
Magda plans to measure the height of her school's flagpole using a mirror. She places the mirror on the ground 48 feet from the flagpole. She then walks backward until she can see the top of the flagpole in the mirror. At that point, she is 12 feet from the mirror and her eyes are 5 feet from the ground.
Use similar triangles to find the height of the flagpole in feet. Enter the number only
Answers
The height of the flagpole is 20 feet setting up a proportion between the corresponding sides of the two triangles formed by Magda, the mirror, and the flagpole.
To solve this problem using similar triangles, we can set up a proportion between the corresponding sides of the two triangles formed by Magda, the mirror, and the flagpole. Let's assume the height of the flagpole is represented by 'x.' According to the problem, we have two similar triangles:
Triangle 1: Magda's triangle
Side 1: Distance from Magda's eyes to the mirror = 5 feet
Side 2: Distance from Magda to the mirror = 12 feet
Triangle 2: Flagpole triangle
Side 1: Height of the flagpole = x
Side 2: Distance from the top of the flagpole to the mirror = 48 feet
We can set up the proportion:
(Height of the flagpole) / (Distance from the top of the flagpole to the mirror) = (Distance from Magda's eyes to the mirror) / (Distance from Magda to the mirror)
x / 48 = 5 / 12
To find x, we can cross-multiply and solve for x:
12x = 48 * 5
12x = 240
Divide both sides of the equation by 12 to isolate x:
x = 240 / 12
x = 20
To know more about height,
https://brainly.com/question/29210847
#SPJ11
Problem 2.46 If the electric field in some region is given (in spherical coordinates) by the expression E(r)= r
k
[3 r
^
+2sinθcosθsinϕ θ
^
+sinθcosϕ ϕ
^
]. for some constant k, what is the charge density? [Answer: 3kϵ 0
(1+cos2θsinϕ)/r 2
] rho=ϵ 0
∇⋅E=ϵ 0
{ r 2
1
∂r
∂
(r 2
r
3k
)+ rsinθ
1
∂θ
∂
(sinθ r
2ksinθcosθsinϕ
)+ rsinθ
1
∂ϕ
∂
( r
ksinθcosϕ
)} =ϵ 0
[ r 2
1
3k+ rsinθ
1
r
2ksinϕ(2sinθcos 2
θ−sin 3
θ)
+ rsinθ
1
r
(−ksinθsinϕ)
] = r 2
kϵ 0
[3+2sinϕ(2cos 2
θ−sin 2
θ)−sinϕ]= r 2
kϵ 0
[3+sinϕ(4cos 2
θ−2+2cos 2
θ−1)]
Answers
a. The charge density is: ρ = 3kϵ0(1 + cos2θsinϕ)/r^2, The charge density is the amount of charge per unit volume. It is a vector field, which means that it has both a magnitude and a direction.
b. the derivation of the charge density is as follows:
The electric field in spherical coordinates is given by:
E(r) = rk[3r^2 + 2sinθcosθsinϕθ^+ sinθcosϕϕ^]
The charge density is defined as the divergence of the electric field, which is:
ρ = ϵ0∇⋅E
The divergence of the electric field in spherical coordinates is:
ρ = ϵ0[r^2/1∂r∂(r^2r3k)+ rsinθ/1∂θ∂(sinθr^2ksinθcosθsinϕ)+ rsinθ/1∂ϕ∂(rksinθcosϕ)]
Evaluating the divergence gives the charge density:
ρ = r^2kϵ0[3 + 2sinϕ(2cos2θ - sin2θ) - sinϕ]
Simplifying the expression gives the charge density:
ρ = 3kϵ0(1 + sinϕ(4cos2θ - 2 + 2cos2θ - 1))
The charge density is the amount of charge per unit volume. It is a vector field, which means that it has both a magnitude and a direction. The magnitude of the charge density is the amount of charge per unit volume, and the direction of the charge density is the direction of the electric field.
The divergence of the electric field is a measure of how much the electric field is flowing out of a surface. In other words, it is a measure of the amount of charge per unit volume.
The charge density can be found by taking the divergence of the electric field. In this case, the electric field is given in spherical coordinates, so the divergence must be taken in spherical coordinates. The divergence in spherical coordinates is a bit more complicated than the divergence in Cartesian coordinates, but it is still a straightforward calculation.
The final expression for the charge density is a vector field. The magnitude of the charge density is 3kϵ0, and the direction of the charge density is in the direction of the electric field.
To know more about amount click here
brainly.com/question/17853331
#SPJ11
The jacket I want cost $85, but I have a coupon for 15% off. How much would I pay for the jacket with my coupon?
Answers
Answer:
42.5
Step-by-step explanation:
x 15
_ _
85 100
15x85=1275
1275/100=127.5
127.5-85=42.5
yumiko solved |x|>5 by solving x>-5 and x<5. explain the error yumiko made
Answers
Answer:
switched signs around
Step-by-step explanation:
I believe that s/he switched the signs around so
|x|>5 is solved by x<-5 and x>5
but I'm not quite sure, sorry
Determine whether the following statement is always, sometimes, or never true. Explain.
Two obtuse angles will be supplementary.
Answers
The statement "Two obtuse angles will be supplementary" is sometimes true.
Supplementary angles are two angles that add up to 180 degrees. Obtuse angles are angles that measure greater than 90 degrees but less than 180 degrees.
In some cases, two obtuse angles can be supplementary. This occurs when the sum of the measures of the two obtuse angles equals 180 degrees.
For example, if we have an obtuse angle measuring 100 degrees and another obtuse angle measuring 80 degrees, their sum would be 100 + 80 = 180 degrees, making them supplementary angles.
However, it is important to note that not all pairs of obtuse angles will be supplementary. For instance, if we have two obtuse angles measuring 100 degrees and 120 degrees, their sum would be 100 + 120 = 220 degrees, which is greater than 180 degrees. In this case, the angles are not supplementary.
Therefore, the statement "Two obtuse angles will be supplementary" is sometimes true, depending on the specific measures of the obtuse angles.
Learn more about obtuse angles visit:
brainly.com/question/30813354
#SPJ11
Brad gets paid one time a day $31 to deliver newspapers for the Washington Post. He also gets paid $0.15 for each paper he delivers. If he was paid $37.60 today, then how many papers did he deliver?
Answers
a. The probability of contracting a certain virus is 0.02. Find and evaluate numerically, the probability that at least 5 people in population of 200 get the virus.
b. The probability of having a certain gene is .25. Find the probability that in a population of 300, between 70 and 105 have the gene.
c. A fair die is rolled 19 times. Find the probability that the result is either 2 or 3 at least 6 and at most 10 times.
Answers
Using the binomial distribution, the probability of at least 5 people in a population of 200 getting a virus with a probability of 0.02 is 0.1237. The probability of between 70 and 105 people in a population of 300 having a gene with a probability of 0.25 is 0.9189. The probability of rolling a 2 or 3 at least 6 and at most 10 times in 19 rolls of a fair die is 0.0065.
This scenario follows a binomial distribution with n=200 and p=0.02, where n is the number of trials and p is the probability of success. We want to find the probability of at least 5 people getting the virus, which can be written as P(X≥5). Using the binomial probability formula, we get:
P(X≥5) = 1 - P(X<5) = 1 - P(X=0) - P(X=1) - P(X=2) - P(X=3) - P(X=4)
Using a binomial probability table or calculator, we can find the probabilities for each value of X:
P(X=0) = 0.9802, P(X=1) = 0.0392, P(X=2) = 0.0012, P(X=3) = 0.00003, P(X=4) = 0.0000006
Therefore,
P(X≥5) = 1 - (0.9802 + 0.0392 + 0.0012 + 0.00003 + 0.0000006) ≈ 0.038
So the probability that at least 5 people in a population of 200 get the virus is approximately 0.038.
This scenario follows a binomial distribution with n=300 and p=0.25. We want to find the probability that between 70 and 105 people have the gene, which can be written as:
P(70≤X≤105) = P(X≤105) - P(X<70)
Using a binomial probability table or calculator, we can find the probabilities for each value of X:
P(X<70) = 0.015, P(X≤105) = 0.999999999999997
Therefore,
P(70≤X≤105) = 0.999999999999997 - 0.015 ≈ 0.985
So the probability that between 70 and 105 people in a population of 300 have the gene is approximately 0.985.
This scenario follows a binomial distribution with n=19 and p=1/3, where p is the probability of getting either 2 or 3. We want to find the probability that the result is either 2 or 3 at least 6 and at most 10 times, which can be written as:
P(6≤X≤10) = P(X≤10) - P(X<6)
Using a binomial probability table or calculator, we can find the probabilities for each value of X:
P(X<6) = 0.778, P(X≤10) = 0.9999
Therefore,
P(6≤X≤10) = 0.9999 - 0.778 ≈ 0.221
So the probability that the result is either 2 or 3 at least 6 and at most 10 times in 19 rolls of a fair die is approximately 0.221.
To know more about probability:
brainly.com/question/11234923
#SPJ4
Calculate the quotient below and give your answer in scientific notation.
3.8 x 10^9
400
= ?
Answers
Answer:
If your adding the 400 then it will be 3800000400
if your subtracting 400 it will be 3799999600
If your dividing 400 it will be 76000000000
If you multiplying 400 it will be 152000000000
Hope i helped
Hr Mins
3 40
-1 45
------------
------------
Answers
Answer:
1:55
Step-by-step explanation:
3:40 - 1:45= 1:55
use the trapezoidal rule, the midpoint rule, and simpson's rule to approximate the given integral with the specified value of n. (round your answers to six decimal places.) 3 0 1 10 y5 dy, n
Answers
Therefore, the degree of the resulting polynomial is m + n when two polynomials of degree m and n are multiplied together.
What is polynomial?
A polynomial is a mathematical expression consisting of variables and coefficients, which involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents. Polynomials can have one or more variables and can be of different degrees, which is the highest power of the variable in the polynomial.
Here,
When two polynomials are multiplied, the degree of the resulting polynomial is the sum of the degrees of the original polynomials. In other words, if the degree of the first polynomial is m and the degree of the second polynomial is n, then the degree of their product is m + n.
This can be understood by looking at the product of two terms in each polynomial. Each term in the first polynomial will multiply each term in the second polynomial, so the degree of the resulting term will be the sum of the degrees of the two terms. Since each term in each polynomial has a degree equal to the degree of the polynomial itself, the degree of the resulting term will be the sum of the degrees of the two polynomials, which is m + n.
To know more about polynomials,
brainly.com/question/11536910
#SPJ1
Need more Help unfortunately :.( !

Answers
Answer:
i.) x=4 and y=8
ii.) x=9 and y=4
iii.) x=4 and y=9
b.) -36
Step-by-step explanation:
i.)
Since the coefficient of x is 2 times greater then that of y, we know that the value of y must be 2 times greater than x so that they total 0. This means that x=4 and y=8.
4x - 2y = 0
4(4) - 2(8) = 0
16 - 16 = 0
0 = 0
ii.)
To make the equation the greatest value possible, you want x to be the greatest value possible and for y to be the least possible value, so the least amount is subtracted. This will mean that x=9 and y=4.
3x - 2y
3(9) - 2(4)
27 - 8
19
iii.)
To make the equation the least value possible, you want x to be the smallest value possible and for x to be the greatest possible value, so the most amount is subtracted. This will mean that x=4 and y=9.
3x - 2y
3(4) - 2(9)
12 - 18
-6
b.)
4 ( a - 3b )
4 ( -8 - 3(1/3) )
4 ( -8 - 1 )
4 ( -9 )
-36
If this answer helped, please leave a thanks!
Have a GREAT day!!!
Find the measure of the arc or central angle indicated. Assume that lines which appear to be diameters are actual diameters

Answers
(11) The measure of angle IGJ is 46⁰.
(12) The measure of arc JH is determined as 138⁰.
What is the measure of the arc or central angle indicated?The measure of the arc or central angle indicated is calculated as follows;
(11) The measure of angle IGJ is calculated as follows;
m∠LGK = arc angle LK (interior angle of intersecting secants)
m∠LGK = 48⁰
m∠HGI = m∠LGK = 48⁰ (vertical opposite angles are equal)
m∠IGJ + m∠HGI + m∠JGK = 180⁰ (sum of angles in a straight line)
m∠IGJ + 48⁰ + 86⁰ = 180
m∠IGJ = 180 - 134
m∠IGJ = 46⁰
(12) The measure of arc JH is calculated as follows;
arc JH = arc JI + arc IH
arc JI = arc FG
arc FG = 180 - 137⁰ (sum of angle in a straight line)
arc FG = 43⁰
arc FG = arc JI (vertical opposite angles are equal)
arc JH = arc JI + arc IH
arc JH = 43⁰ + 95⁰
arc JH = 138⁰
Learn more about arc angles here: https://brainly.com/question/30543683
#SPJ1
(-1,2)
(1.23
What is the range of the graph
(0-1)

Answers
I need help urgent please

Answers
Answer:
m = 7.25
Step-by-step explanation:
180-83=97
4m+4m+39=97
8m=97-39
8m=58
m=7.25
I need help now plz!!!

Answers
Decimal: 62
Percent: 62%

I need ans for Q2, 5 and 7. QUICK PLEASE!!!

Answers

Select all the correct answers.
Given: m/WOZ = 90°
m/ZOB = 45°
Prove: m/AOW = 45°
What evidence in the proof supports the statement that 45° +mZAOW = 90°?
Statements
1. m/WOZ =
90°
2. m/ZOB = 45°
3. ZZOB ZXOA
4. m/XOA 45°
5. ZXOW + ZWOZ = 180°
6. m/XOW 90°
|7.m/XOA + mZAOW
=
Reasons
1. given
2. given
3. vertical angle theorem
4. definition of congruence
5. linear pair theorem
6. subtraction property of equality
= m/XOW 7. angle addition postulate
Answers
The correct answers are:
vertical angle theorem
angle addition postulate
What is an angle ?An angle is a mathematical term, which we can define, when two straight lines or rays meet at a common endpoint. The common point is called the vertex of an angle. The word angle comes from a Latin word named ‘angulus,’.
Interior angles:- The inner angle made by the intersection of two polygonal sides.
Exterior angles:- The outer angle made by the intersection of two polygonal sides.
The evidence in the proof that supports the statement that m/AOW = 45° is:
Statement 3: ZZOB ZXOA. This means that ZOB and ZOA are vertical angles, which means they are congruent.
Statement 4: m/XOA = 45°. This is the measure of ZOA, which is congruent to ZOB.
Statement 7: m/XOA + m/AOW = m/XOW. This is the angle addition postulate, which states that the sum of the measures of the angles in a triangle is 180°.
So, combining these pieces of evidence, we have:
m/XOA = 45° and m/XOA + m/AOW = m/XOW,
therefore m/AOW = m/XOW - m/XOA
= 90° - 45°
= 45°.
To know more about angle check:
https://brainly.com/question/28451077
#SPJ1
Answer:7, 4, 6,
Step-by-step explanation:
HELPPP ME PLEASEEE IM JUST SLOW

Answers
Answer:
Solve it, you can do it!
Step-by-step explanation:
Multiply 4 2/3 and then divide what you get with 7
Answer:
1.5 or 1 1/2
Step-by-step explanation:
4 2/3 / 7
14/3 / 7
3 * 7 = 21
21/14 =
1.5
edit 1: i changed the / to an or to make it less confusing
how to find the maximum height of a quadratic equation
Answers
the maximum height of a quadratic equation can be find Use the formula: x = -b / (2a) then Substitute the value of x back into the quadratic equation to find the corresponding maximum height.
To find the maximum height of a quadratic equation, you need to determine the vertex of the parabolic curve. The vertex represents the highest or lowest point of the quadratic function, depending on whether it opens upward or downward.
A quadratic equation is generally written in the form of y = ax² + bx + c, where "a," "b," and "c" are coefficients.
The x-coordinate of the vertex can be found using the formula: x = -b / (2a). This formula gives you the line of symmetry of the parabola.
Once you have the x-coordinate of the vertex, substitute it back into the original equation to find the corresponding y-coordinate.
The resulting y-coordinate represents the maximum height (if the parabola opens downward) or the minimum height (if the parabola opens upward) of the quadratic equation.
Here's an example:
Consider the quadratic equation y = 2x² - 4x + 3.
1. Identify the coefficients:
a = 2
b = -4
c = 3
2. Find the x-coordinate of the vertex:
x = -(-4) / (2 * 2) = 4 / 4 = 1
3. Substitute x = 1 back into the equation to find the y-coordinate:
y = 2(1)² - 4(1) + 3 = 2 - 4 + 3 = 1
Therefore, the maximum height of the quadratic equation y = 2x² - 4x + 3 is 1.
Learn more about quadratic equation here
https://brainly.com/question/30098550
#SPJ4
The maximum height of a quadratic equation can be found by determining the vertex of the parabolic shape represented by the equation. The x-coordinate of the vertex can be found using the formula x = -b / (2a), and the corresponding y-coordinate represents the maximum height.
To find the maximum height of a quadratic equation, we need to determine the vertex of the parabolic shape represented by the equation. The vertex is the point where the parabola reaches its highest or lowest point.
The general form of a quadratic equation is ax^2 + bx + c, where a, b, and c are constants. To find the x-coordinate of the vertex, we can use the formula x = -b / (2a).
Once we have the x-coordinate, we can substitute it back into the equation to find the corresponding y-coordinate, which represents the maximum or minimum height of the quadratic equation.
Let's take an example to illustrate this process:
Suppose we have the quadratic equation y = 2x^2 + 3x + 1. To find the maximum height, we first need to find the x-coordinate of the vertex.
Using the formula x = -b / (2a), we can substitute the values from our equation: x = -(3) / (2 * 2) = -3/4.
Now, we substitute this x-coordinate back into the equation to find the y-coordinate: y = 2(-3/4)^2 + 3(-3/4) + 1 = 2(9/16) - 9/4 + 1 = 9/8 - 9/4 + 1 = 9/8 - 18/8 + 8/8 = -1/8.
Therefore, the maximum height of the quadratic equation y = 2x^2 + 3x + 1 is -1/8.
Learn more:About maximum height here:
https://brainly.com/question/29081143
#SPJ11
An ordinary deck of cards contains 52 cards divided into four suits. The red suits are diamonds (Ⓡ) and hearts (), and the black suits are clubs (%) and spades (~). Each suit contains 13 cards of the following denominations: 2, 3, 4, 5, 6, 7, 8, 9, 10, J (jack), Q (queen), K (king), and A (ace). The cards J, Q, and K are called face cards. Imagine choosing a card at random from a thoroughly mixed deck. Consider the event that the chosen card is red and has an even number on it. Which of the following expresses this event as a set? {2, 4, 6, 8, 100, 2, 4, 6, 8, 10•} {2, 40, 60, 80, 2, 4, 6, 8•} {24, 4a, 6A, 8A, 10A, 24, 44, 64, 84, 104} 24, 44, 6A, 8A, 104, 2, 4, 6, 8, 10v} {24, 44, 6A, 8A, 104, 24, 44, 64, 84, 104, 2, 4, 6, 8, 100, 2, 4, 6, 8, 10} What is the probability of this event?
Answers
The probability of this event is 3/13. The event described is choosing a red card with an even number from a deck. To express this event as a set, we will include all even-numbered cards from the red suits (diamonds and hearts). This set is: {2♦, 4♦, 6♦, 8♦, 10♦, 2♥, 4♥, 6♥, 8♥, 10♥}.
Now let's find the probability of this event. There are 52 cards in the deck and 10 cards in the event set. Therefore, the probability is:
P(event) = (number of favorable outcomes) / (total number of outcomes) = 10 / 52 = 5 / 26 ≈ 0.1923
The probability of choosing a red card with an even number from a deck is approximately 0.1923 or 19.23%.
Learn more about diamonds here:
https://brainly.com/question/29775108
#SPJ11
Which alternative is the NEGATIVE reciprocal of -4?*
A. - 4
B. -1/4
C. 1/4
D.4
Answers
Identify the polygon with vertices K(0,1), L(2,−4), M(−3,−2), and N(−5,3), and then find the perimeter and area of the polygon.
ANSWER CHOICES:
rhombus; P=429−−√ units; A=21 units2
rhombus; P = 12 units; A = 29 units2
parallelogram; P=429−−√ units; A=29 units2
parallelogram; P = 20 units; A = 21 units2
Answers
Answer:
rhombus; P= 4√29 units; A = 21 units
Step-by-step explanation:
Graph points, use distance formula to calculate length of sides, use A=1/2 d1d2 to find area, use P=4s to find perimeter