For the differential equation s" + bs' +9s = 0, find the values of b that make the general solution overdamped, underdamped, or critically damped. (For each, give an interval or intervals for b for which the equation is as indicated. Thus if the the equation is overdamped for all b in the range -1
Answers
The general solution to the differential equation s" + b s' + 9s = 0 can be written as:
\(s(t) = c1*e^(-bt/2)*cos(({4b-36)/2)t} 4b-36)/2)t) + c2e^(-bt/2)*sin\sqrt{(4b-36)/2)*t)} (4b-36)/2)*t)\)
where c1 and c2 are constants determined by the initial conditions.
The behavior of the solutions to this equation depends on the value of the parameter b. Specifically, there are three cases to consider:
Overdamped: If b > 6, then the roots of the characteristic equation\(s^2 + bs + 9 = 0\) are real and distinct, i.e., \(b^2 - 4ac\) > 0. In this case, the general solution is a linear combination of two decaying exponentials, and the system is said to be overdamped. To find the interval for b for which the equation is overdamped, we solve the inequality b > 6, which gives the interval (6, infinity).
Critically damped: If b = 6, then the roots of the characteristic equation are real and equal, i.e., \(b^2 - 4ac\)= 0. In this case, the general solution is a linear combination of two decaying exponentials, where one of the exponentials has an additional factor of t. The system is said to be critically damped. To find the interval for b for which the equation is critically damped, we solve the equation b = 6, which gives the singleton set {6}.
Underdamped: If b < 6, then the roots of the characteristic equation are complex conjugates, i.e., \(b^2 - 4ac\) < 0. In this case, the general solution is a linear combination of two decaying exponentials, where the exponentials have a sinusoidal factor. The system is said to be underdamped. To find the interval for b for which the equation is underdamped, we solve the inequality b < 6, which gives the interval (-infinity, 6).
Therefore, the interval for b that makes the general solution overdamped is (6, infinity), the singleton set {6} makes the general solution critically damped, and the interval for b that makes the general solution underdamped is (-infinity, 6).
Learn more about differential equation : https://brainly.com/question/18760518
#SPJ11
Related Questions
The town of Mathville is triangular in shape and has a perimeter of 104 km. The interstate borders the southern part of the town, but town residents want to build two more roads, one on each side of the town. The length of one side of the town is ½ the length of the interstate. The length of the other side is 2/3 the length of the interstate. Determine the length of road necessary to complete the town’s task. That is, determine the length of each of the two sides of the town not bordered by the interstate.
Answers
Let's solve this step by step.
Let's denote the length of the interstate as "x".
According to the given information, one side of the town is 1/2 the length of the interstate, which means its length is (1/2)x.
Another side of the town is 2/3 the length of the interstate, which means its length is (2/3)x.The perimeter of the town is the sum of the lengths of all three sides:
Perimeter = (1/2)x + (2/3)x + x
We know that the perimeter is 104 km, so we can set up the equation:
104 = (1/2)x + (2/3)x + x
To simplify the equation, let's find the common denominator of 2 and 3, which is 6:
104 = (3/6)x + (4/6)x + (6/6)x
Now, we can add the fractions:
104 = (13/6)x
To isolate x, we multiply both sides of the equation by 6/13:
104 * (6/13) = x
48 = x
So, the length of the interstate is 48 km.
Now we can find the lengths of the other two sides of the town:Length of one side = (1/2) * 48 = 24 km
Length of the other side = (2/3) * 48 = 32 km
Therefore, the length of the side not bordered by the interstate are 24 km and 32 km, respectively.
Given that the town is triangular in shape with a perimeter of 104 km, one side of the town is half the length of the interstate, while the other side is two-thirds the length of the interstate. By solving the equations derived from these conditions, we find that the length of each of the two sides not bordered by the interstate is 24 km and 32 km, respectively.
Let's denote the length of the interstate as "x" km. According to the given information, one side of the town is half the length of the interstate, so its length is x/2 km. The other side is two-thirds the length of the interstate, making it (2/3)x km.
Since the town is triangular, the sum of all three sides must equal the perimeter of the town, which is 104 km. Therefore, we can write the equation:
x + x/2 + (2/3)x = 104
To solve for x, we can simplify the equation:
(6/6)x + (3/6)x + (4/6)x = 104
(13/6)x = 104
To isolate x, we multiply both sides by 6/13:
x = (6/13) * 104
x = 48 km
Now that we have the length of the interstate, we can determine the lengths of the other two sides. One side is half the length of the interstate, so it is (1/2) * 48 = 24 km. The other side is two-thirds the length of the interstate, so it is (2/3) * 48 = 32 km.
Therefore, the length of each of the two sides of the town not bordered by the interstate is 24 km and 32 km, respectively.
Read more about interstate here:
brainly.com/question/32495419
The intersection of two streets forms a parallelogram. One street is 40 feet wide. The height of the parallelogram formed is 25 ft. What is the area of the intersection?
Answers
Answer:
1000 feet²
Step-by-step explanation:
Given that,
Width of a parallelogram is 40 feet
Height of the parallelogram is 25 feet
We need to find the area of the intersection that forms a parallelogram. The formula for the area of a parallelogram is given by :
A = base × height
A = 40 × 25
A = 1000 feet²
So, the area of the parallelogram is 1000 feet²
Which correctly describes this rotation?
A. a counterclockwise rotation of 30° about point A
B. a counterclockwise rotation of 45° about point A
c. a counterclockwise rotation of 90° about point A
D. a counterclockwise rotation of 180° about point A

Answers
safety data sheets are only required when there are 10 gallons true or false
Answers
Safety data sheets (SDS) are not only required when there are 10 gallons. This statement is false. SDS, also known as material safety data sheets (MSDS), are required for hazardous substances, regardless of the quantity.
Safety data sheets provide detailed information about the potential hazards, handling, and emergency measures for substances. They are required under various regulations, such as the Occupational Safety and Health Administration (OSHA) Hazard Communication Standard (HCS) in the United States.
The quantity of the substance does not determine the need for an SDS. For example, even if a small amount of a highly hazardous substance is present, an SDS is still necessary for safety reasons.
SDS help workers and emergency personnel understand the risks associated with a substance and how to handle it safely. It is essential to follow proper safety protocols and provide SDS for hazardous substances, regardless of the quantity.
To know more about Protocols visit.
https://brainly.com/question/28782148
#SPJ11
Find the smallest number by which 3^6*3^5 must be multiplied (or divided)so that the product (or quotient) becomes a perfect square
Answers
The smallest number by which 3^6 * 3^5 must be multiplied (or divided) to become a perfect square is 2.
To find the smallest number by which 3^6 * 3^5 must be multiplied (or divided) so that the product (or quotient) becomes a perfect square,
First, let's simplify the expression 3^6 * 3^5 by using the exponent rule for multiplication. When we multiply numbers with the same base, we add the exponents:
3^6 * 3^5 = 3^(6+5) = 3^11.
Now, we have 3^11. To make this expression a perfect square, we need the exponent to be an even number. In this case, we want the exponent of 3 to be divisible by 2.
The smallest number by which we can multiply 3^11 to make it a perfect square is 2. By multiplying 3^11 by 2, we get:
2 * 3^11 = (2^2) * (3^11) = (2*3)^11 = 6^11.
Now, 6^11 is a perfect square because the exponent of 6 (11) is divisible by 2. Therefore, the smallest number by which 3^6 * 3^5 must be multiplied to become a perfect square is 2.
To find the smallest number by which 3^6 * 3^5 must be multiplied (or divided) so that the product (or quotient) becomes a perfect square, we need to simplify the expression 3^6 * 3^5. By applying the exponent rule for multiplication, we can add the exponents:
3^6 * 3^5 = 3^(6+5) = 3^11.
Now, we have the expression 3^11. To make it a perfect square, we need the exponent of 3 to be divisible by 2. Since 11 is an odd number, we need to multiply or divide 3^11 by a number that will make the exponent even.
The smallest number by which we can multiply 3^11 to make it a perfect square is 2. By multiplying 3^11 by 2, we get:
2 * 3^11 = (2^1) * (3^11) = (2*3)^11 = 6^11.
Now, 6^11 is a perfect square because the exponent of 6 (11) is divisible by 2.
Therefore, the smallest number by which 3^6 * 3^5 must be multiplied (or divided) to become a perfect square is 2.
Learn more about expression
brainly.com/question/34132400
#SPJ11
A square could be called a _____ since it has four right angles.
Answers
A square could be called a rectangle since it has four right angles.
A rectangle is a type of quadrilateral, whose opposite sides are equal and parallel. It is a four-sided polygon that has four angles, equal to 90 degrees. A rectangle is a two-dimensional shape.
A rectangle is a closed two-dimensional figure with four sides. The opposite sides of a rectangle are equal and parallel to each other and all the angles of a rectangle are equal to 90°. Observe the rectangle given below to see its shape, sides and angles.
So, Every square is a rectangle because it is a quadrilateral with all four angles right angles.
Learn more about Rectangle at:
https://brainly.com/question/29123947
#SPJ4
what fraction is equivlant to 2/6
Answers
Answer:
1/3
Step-by-step explanation:
The simplest form of 2/6 is 1/3. You can do 2/6*.5/.5 to get 1/3
You can do other fractions such as 4/12, 8/24, as long as it the numerator maintains a ratio of 1:3
Find the arc length and sector area in terms
NEED ASAP please

Answers
The value of the arc length and area are 11. 2ft and 44.2 ft² respectively
How to determine the valueTo determine the arc length, we use the formula;
s = 2πr(θ/360)
Such that the parameters of the formula are expressed as;
s is the arc lengthr is the radiusθ is the angle in degreesSubstitute the values, we get;
s = 2 × 3.14 × 8 × (80/360)
Divide the values, we get;
s = 50. 24(0. 22)
Multiply the values, we have;
s = 11. 2ft
The area of the sector is expressed as;
(θ/360º) × πr2
Substitute the values
80/360 × 3.14 ×8²
Find the square and multiply
0. 22 × 200. 96
Multiply
44.2 ft²
Learn about arc at: https://brainly.com/question/28108430
#SPJ1
suppose ????:ℝ3⟶ℝ is a differentiable function which has an absolute maximum value ????≠0 and an absolute minimum m . suppose further that m
Answers
If a differentiable function f: ℝ³ ⟶ ℝ has an absolute maximum value K ≠ 0 and an absolute minimum m, then the function f must have a critical point where the derivative of the function is zero (or undefined).
Given that, suppose f : ℝ³ ⟶ ℝ is a differentiable function which has an absolute maximum value K ≠ 0 and an absolute minimum m.
Since f is continuous on a compact set, it follows that f has a global maximum and a global minimum. We are given that f has an absolute maximum value K ≠ 0 and an absolute minimum m. Then there exists a point a ∈ ℝ³ such that f(a) = K and a point b ∈ ℝ³ such that f(b) = m.Then f(x) ≤ K and f(x) ≥ m for all x ∈ ℝ³.
Since f(x) ≤ K, it follows that there exists a sequence {x_n} ⊆ ℝ³ such that f(x_n) → K as n → ∞. Similarly, since f(x) ≥ m, it follows that there exists a sequence {y_n} ⊆ ℝ³ such that f(y_n) → m as n → ∞.Since ℝ³ is a compact set, there exists a subsequence {x_nk} and a subsequence {y_nk} that converge to points a' and b' respectively. Since f is continuous, it follows that f(a') = K and f(b') = m.
Since a' is a limit point of {x_nk}, it follows that a' is a critical point of f, i.e., ∇f(a') = 0 (or undefined). Similarly, b' is a critical point of f. Therefore, f has at least two critical points where the derivative of the function is zero (or undefined). Hence, the statement is true.
Therefore, the above explanation is verified that if a differentiable function f: ℝ³ ⟶ ℝ has an absolute maximum value K ≠ 0 and an absolute minimum m, then the function f must have a critical point where the derivative of the function is zero (or undefined).
Know more about differentiable function here,
https://brainly.com/question/30079101
#SPJ11
Select all expressions that are equal to 3⋅3⋅3⋅3⋅3
a) 3 ⋅ 5
(b) 3^5
(c) 3^4 ⋅ 3
(d) 5 ⋅ 3
(e) 5^3
Answers
because they all add up to 243
but a, d, and e don’t.
For what value of k does the equation have no solution? kx - 4 = 5x + 8
Answers
Answer:
Your answer is: k = 5+12/x
Isolate the variable by dividing each side by factors that don't contain the variable.
Step-by-step explanation:
Hope this helped : )

It is Friday and you and your friends are going to hit up
the local amusement park. The park costs $30 dollars
to enter and then the tickets for the rides each cost
$3.50. Write an equation when y is total price of
amusement park and x is the number of tickets bought.
Interpret the slope and y-intercept when asked to
explain your answer
Helpp plss
Answers
Answer:
y= 30 + 3.50
Step-by-step explanation:
lol I think you're Giselle for my school but that's what the answer it im pretty sure.
4m+2n=5n (solve for m)
Answers
M = 3n/4
Give me 5 stars if it helps
Answer:
m=3n/4
Step-by-step explanation:
4m+2n=5n subtract 2n from both sides
4m= 5n-2n combine like terms
4m=3n divide by 4
m=3n/4
brainliest plz <3
What angular resolution would you need to see the Sun and Jupiter as distinct points of light? Express your answer in arcseconds to two significant figures. Jupiter 195| ΑΣΦ % ? 11 Suppose you were looking at our own solar system from a distance of 6.0 light-years.
Answers
An angular resolution of 0.56 arcseconds is required to see the Sun and Jupiter as separate objects. This is an extremely small angle and would necessitate the use of a large telescope.
Angular resolution is defined as the minimum angle between two objects that enables a viewer to see them as distinct objects rather than as a single one. A better angular resolution corresponds to a smaller minimum angle. The angular resolution formula is θ = 1.22 λ / D, where λ is the wavelength of light and D is the diameter of the telescope. Thus, the angular resolution formula can be expressed as the smallest angle between two objects that allows a viewer to distinguish between them. In arcseconds, the answer should be given to two significant figures.
To see the Sun and Jupiter as distinct points of light, we need to have a good angular resolution. The angular resolution is calculated as follows:
θ = 1.22 λ / D, where θ is the angular resolution, λ is the wavelength of the light, and D is the diameter of the telescope.
Using this formula, we can find the minimum angular resolution required to see the Sun and Jupiter as separate objects. The Sun and Jupiter are at an average distance of 5.2 astronomical units (AU) from each other. An AU is the distance from the Earth to the Sun, which is about 150 million kilometers. This means that the distance between Jupiter and the Sun is 780 million kilometers.
To determine the angular resolution, we need to know the wavelength of the light and the diameter of the telescope. Let's use visible light (λ = 550 nm) and assume that we are using a telescope with a diameter of 2.5 meters.
θ = 1.22 λ / D = 1.22 × 550 × 10^-9 / 2.5 = 2.7 × 10^-6 rad
To convert radians to arcseconds, multiply by 206,265.θ = 2.7 × 10^-6 × 206,265 = 0.56 arcseconds
The angular resolution required to see the Sun and Jupiter as distinct points of light is 0.56 arcseconds.
This is very small and would require a large telescope to achieve.
In conclusion, we require an angular resolution of 0.56 arcseconds to see the Sun and Jupiter as separate objects. This is an extremely small angle and would necessitate the use of a large telescope.
To know more about angular resolution visit:
brainly.com/question/31858807
#SPJ11
uanita's number of shells is 5 less than twice Aimee's number of shells. Let x represent Aimee's number of shells, and let y represent Juanita's number of shells. Which ordered pair (x, y) satisfies the equation y = 2x − 5?
Answers
Answer:
c 3 and 6
Step-by-step explanation:
edg2020
Answer:
C 6 and 3, not 3 and 6
Step-by-step explanation:
got it wrong and saw the answer
what 2095a-4235b-5326a=
Answers
Answer:
-3231a-5326b
Step-by-step explanation:
I subtracted the a's but you can't subtract the b with anything so .....yea
for each of the following find all rational roots of the polynomial equation 2x cube - 5 x square + 1=0
Answers
Given:
The equation of polynomial is
\(2x^3-5x^2+1=0\)
To find:
All rational roots of the polynomial.
Solution:
According to the rational root theorem, all the possible rational roots of a polynomial are defined as
\(x=\dfrac{p}{q}\)
where, p is a factor of constant term and q is factor of leading coefficient.
We have,
\(2x^3-5x^2+1=0\)
Here, leading coefficient is 2 and constant term is 1.
Factors of 1 are ±1.
Factors of 2 are ±1, ±2.
Using rational root theorem, we get
\(x=\pm \dfrac{1}{1},\pm \dfrac{1}{2}\)
\(x=\pm 1,\pm \dfrac{1}{2}\)
Therefore, all possible rational roots of the given polynomial are \(\pm 1,\pm \dfrac{1}{2}\).
As the number of degrees of freedom for a t distribution increases, the difference between the t distribution and the standard normal distribution.
Answers
The standard normal distribution becomes smaller.
What is standard deviation?
Your dataset's average level of variability is represented by the standard deviation. It reveals the average deviation of each statistic from the mean. A low standard deviation denotes that values are grouped close to the mean, whereas a large standard deviation shows that values are often far from the mean.Think about the following data: 2, 1, 3, 2, 4. The average and the sum of squares representing the observations' variances from the mean will be 2.4 and 5.2, respectively. This means that (5.2/5) = 1.01 will be the standard deviation.As the number of degrees of freedom for a t distribution increases, the difference between the t distribution and the standard normal distribution
becomes smaller.
Learn more about standard deviation
brainly.com/question/13905583
#SPJ4
There are 12 eggs in a dozen. Write an algebraic expression for the number of eggs in d dozen.
Answers
Answer:
4d=48
Step-by-step explanation:
What is Y=-4 y=x-8 answer?
Answers
Answer
x=4
Explanation
-4 = x -8
add 8 to both sides
-4+8 = x
x=4
f(x) = |x – 3| + 6 where is the vertex of the graph
Answers
Answer: (3,6)
Rewrite in vertex form and use this form to find the vertex (h,k)
Answer:
(3,6)
Step-by-step explanation:
f(x) = |x| is a V-shaped graph with the vertex at (0,0). It is called a parent graph, because its super basic.
f(x) = |x - 3| + 6
has had two changes made to it. The "- 3" that's in there close to the x slides the graph over to the right 3 units. This is kind of the opposite of what you might think. Minus3 shifts right. (Plus3 would shift left)
The +6 tacked on to the end shifts the whole graph UP 6.
That slides the graph RIGHT3 and UP6. So the vertex lands at (3,6). See image.

The parents are making sandwiches for a class picnic. They have 72 turkey slices, 48 cheese slices and 96 tomato slices. What is the greatest number of sandwiches they can make if each sandwich has the same filing? how many slices of turkey cheese and tomato each sandwich will have.
Answers
Would you multiply M by the third equation (6x^5.....) since it is subtraction

Answers
Answer:
B
Step-by-step explanation:
Here, we want to get the value of m
The value of m can be obtained by multiplying the first factors of the first two polynomial, subtracting the first factor of the third and equating to 18
So what we have will be;
m * 6 - 6 = 18
6m -6 = 18
6m = 18 + 6
6m = 24
m = 24/6
m = 4
find two possible functions f, given the second-order derivative. (enter your answers as a comma-separated list.) f ''(x)
Answers
The two possible functions is F(x)= \frac{x^4}{12}+3x^2 and F(x)= \frac{x^4}{12}+3x^2+x.
The derivative of the first derivative of the given function is known as the second order derivative. We can learn about the slope of the tangent at a particular position or the instantaneous rate of change of a function at that point from the first-order derivative at that point.
F”(x)= x^2+6
F’(x)= \int f"(x) dx
= \int( x^2+6) dx
= \frac{x^3}{3}+6x+c_1 c_1 is the integral constant.
F(x)= \int f\prime(x) dx
= \int f (\frac{x^3}{3}+6x+c_1) dx
= \frac{x^4}{12}+3x^2+c_1x+c_2
(i) if c_1=0 , and c_2=0
F(x)= \frac{x^4}{12}+3x^2
(ii) if c_1=1, and c_2=0
F(x)= \frac{x^4}{12}+3x^2+x
Therefore the two possible functions is F(x)= \frac{x^4}{12}+3x^2 and F(x)= \frac{x^4}{12}+3x^2+x
To learn more about the second-order derivatives visit
https://brainly.com/question/14415022
#SPJ4
Two families attended a baseball game. The first family bought 3 bags of popcorn and 4 souvenir cups, which totaled $40. The second family bought 8 bags of popcorn and 4 souvenir cups, which totaled $60. How much did one bag of popcorn cost?
$4
$5
$6
$7
Answers
Answer: 5$ took test
Step-by-step explanation:
Answer:
Step-by-step explanation:
5 is the answer
The Main Street Animal Hospital can take care of 28 animals at one time. The Green Street Animal Hospital can take care of twice as many animals. How many animals can the Green Street Animal Hospital care for?
Joe's equation: g equals 28 cross times 2
Answers
Answer:
56
Step-by-step explanation:
which graph represents a quadratic function with a vertex at (0,0)
Answers
Answer:
parabola On a coordinate plane, a parabola opens up. It goes through (negative 5, 6), has a vertex of (0, 0), and goes through (5, 6). On a coordinate plane, a parabola opens up.
Step-by-step explanation:
Answer: C) the third graph
Step-by-step explanation: i got 100% on my quiz, hope this helps!!
-19+[27-{14+(5-2)×4÷2
Answers
EXAMPLE QUESTION+ANSWER;-
16 - [5 - 2 { 14 of 2 - (8/4 * 2 - 1 + 3 } ]
= 16 - [5 - 2 { 14 of 2 - (2 * 2 - 1 + 3 } ]
= 16 - [5 - 2 { 14 of 2 - (4 - 1 + 3 } ]
= 16 - [5 - 2 { 14 of 2 - (3 + 3 } ]
= 16 - [5 - 2 { 14 of 2 - 6} ]
= 16 - [5 - 2 { 28 - 6} ]
= 16 - [5 - 2 {22} ]
= 16 - [5 - 44]
= 16 + 30
= 55
Answer: 55
Given a box of coins where exactly half of the coins are fair coins and the other half are loaded coins (phead = 0.9), if you pick one coin from the box and toss it five times, what is the probability to see five heads in a row?
If you randomly pick a coin from the box mentioned above (i.e., half of coins were loaded with phead = 0.9), toss it five times and get five heads. What is the probability that this is a fair coin?
Answers
The probability of seeing five heads in a row when picking a random coin from the box and tossing it five times is approximately 0.29677.
The required probability that the coin is fair given that we observed five heads in a row is approximately 0.05338.
The probability of flipping five heads in a row with a fair coin is,
⇒ (1/2)⁵ = 1/32,
Since the probability of flipping heads on any given toss is 1/2, and each toss is independent.
Then the probability of flipping five heads in a row with a loaded coin (p head = 0.9) be,
⇒ (0.9)⁵ = 0.59049,
Since the probability of flipping heads on any given toss is 0.9, and each toss is independent.
Now, to find the probability of seeing five heads in a row when picking a random coin from the box and tossing it five times,
Use the law of total probability,
Let F denote the event that the coin is fair,
And L denote the event that the coin is loaded.
Then, the probability of seeing five heads in a row is:
⇒P(5 heads) = P(5 heads | F) P(F) + P(5 heads | L) P(L)
= (1/32) (1/2) + (0.59049) (1/2)
= 0.29677
Therefore,
The probability of seeing five heads in a row when picking a random coin from the box and tossing it five times is approximately 0.29677.
Proceed the second question:
We have to find the probability that the coin is fair given that we observed five heads in a row.
Let H denote the event that we observed five heads in a row, and let F and L have the same meanings as before.
Then, by Bayes' theorem, we have:
P(F | H) = P(H | F) P(F) / P(H)
We already have P(H | F) and P(H) in the previous question,
So we just need to compute P(F).
Since half of the coins are fair, we have:
P(F) = 1/2
Putting it all together, we get:
P(F | H) = (1/32) (1/2) / 0.29677
= 0.05338
Therefore, the required probability is approximately 0.05338.
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ1
Please help
Charles correctly answered 23 questions on a test receiving a grade of 92% how many questions where on the test
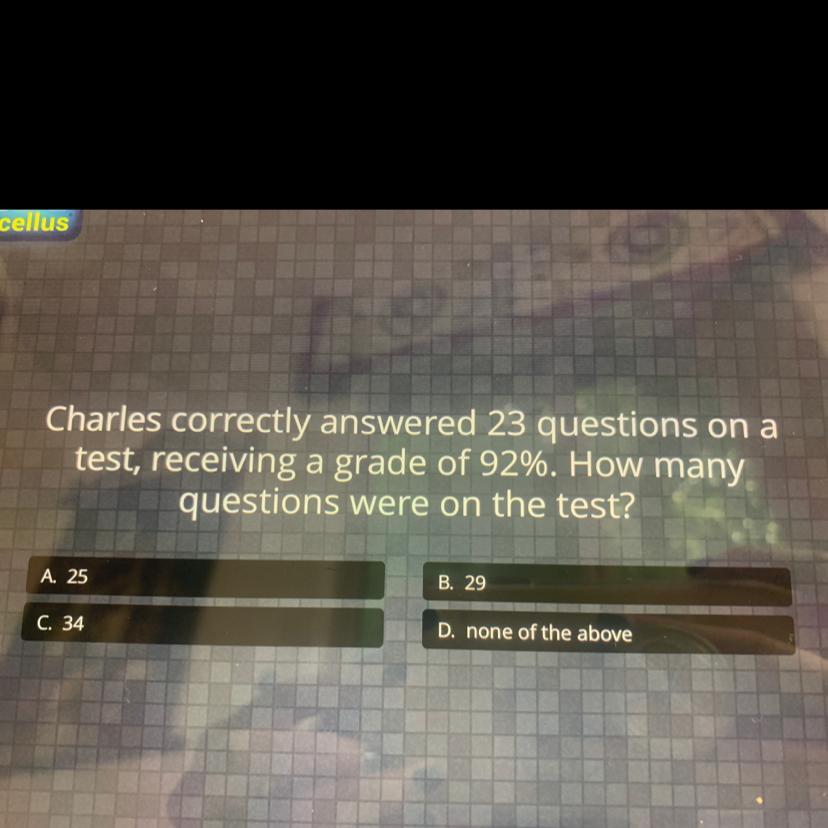
Answers
Answer:
25
Step-by-step explanation:
Cross multiply
23/x=92/100
x=25
There were approximately 25 questions on the test.
To determine the number of questions on the test, we can set up a proportion based on Charles' correct answers and the grade received.
Let x be the total number of questions on the test.
We can set up the proportion:
23 (Charles' correct answers) / x (total number of questions) = 92% (grade as a decimal: 0.92)
This can be written as:
23 / x = 0.92
To solve for x, we can multiply both sides of the equation by x:
23 = 0.92 * x
Dividing both sides by 0.92:
23 / 0.92 = x
x ≈ 25
Therefore, there were approximately 25 questions on the test.
To know more about questions click here:
https://brainly.com/question/11935676
#SPJ2