First to answer will be marked BRAINLIEST and I will give THANKS, please answer the questions directly.

Answers
Answer:
2x+1 (2,7)
Step-by-step explanation:
y=mx+b
Related Questions
i need help with this, it’s due by 12

Answers
Answer:
either y= 5x-3 or y= 3x-3
Step-by-step explanation:
According to the weather report, there is a 25% chance of snow in the mountains tomorrow. how likely is it to snow tomorrow in the mountains?
Answers
It is likely is it to snow tomorrow in the mountains is 1/4
A chance is the occurrence of events without apparent purpose or cause. It is simply the possibility that something will happen. When chance is defined in mathematics, it is called probability. Probability is the extent to which an event is likely to occur, measured by the ratio of favorable cases to the total number of possible cases. Mathematically, the probability that an event occurs is equal to the ratio of the number of cases favorable to a particular event to the number of all possible cases. The theoretical probability of an event is referred to as P(E). P(E) = number of outcomes more favorable to E/Nnumber of all possible outcomes of the experiment
We need to find that what is the chance that it will snow tomorrow in the mountains
According to the weather report, there is a 25% chance of snow in the mountains tomorrow.
Therefore the possible chance that it will snow tomorrow is 25/100 = 1/4
Learn more about possible chances here:
https://brainly.com/question/28052733
#SPJ4
which sets of ordered pairs show equivalent ratios? use the grid to help you. check all that apply
O (1,2), (2, 3), (4, 7)
O (2, 2), (4, 4), (6, 6)
O (3, 1), (4, 1), (5, 1)
O (4, 1), (8, 2), (12, 3)
O (2,1), (4, 3), (5, 4)

Answers
Solve for the value of m

Answers
Answer:
m = 7
Step-by-step explanation:
The 3 given angles lie on a straight line, thus sum to 180° , then
8m - 4 + 90 + 5m + 3 = 180, that is
13m + 89 = 180 ( subtract 89 from both sides )
13m = 91 ( divide both sides by 13 )
m = 7
in the eai sampling problem, the population mean is 51800 and the population standard deviation is 4000 . when the sample size is 64 , what is the probability of obtaining a sample mean within 500 of the population mean.
Answers
the probability of obtaining a sample mean within 500 of the population mean is approximately 0.6827.
To solve this problem, we need to use the central limit theorem which states that the distribution of the sample means will be approximately normal with mean equal to the population mean and standard deviation equal to the population standard deviation divided by the square root of the sample size.
Given that the population mean is 51800 and the population standard deviation is 4000, we can calculate the standard error of the mean as follows:
Standard error of the mean = 4000 / sqrt(64) = 500
We want to find the probability of obtaining a sample mean within 500 of the population mean. This can be written as:
P(51800 - 500 < X < 51800 + 500)
where X is the sample mean.
We can standardize this interval using the standard error of the mean:
P(-1 < Z < 1)
where Z is a standard normal variable.
Using a standard normal table, we find that the probability of Z being between -1 and 1 is approximately 0.6827.
Therefore, the probability of obtaining a sample mean within 500 of the population mean is approximately 0.6827.
To learn more about probability click here:brainly.com/question/31120123
#SPJ11
In the regression model we talked about in class, we assume that for each training data point x, its output value yi is observed. However in some situations that we can not measure the exact value of yi. Instead we only have information about if yi Is larger or less than some value zi. More specifically, the training data is given as a triplet (x,, 2i, bi), where ·Xi Is represented by a vector φ(K)-( 40(Xi), . . . , фМ-1 (Xi)) ' . 2 zi E R is a scalar, bi E 10, 1) is a binary variable indicating that if the true output yi is larger than (b,-1) or not bi 0 Develop a regression model for the ambiguous training data (X,, 2,, bi), i- 1, , n
Answers
ФФФФФФФФФ↑↑→≅≅≅≅≅≅≅≅≅≅НЧШДЦ
Marlin and his brother are going to Antonio, TX next week. They figure that they will drive 792 miles round trip. If their car gets 25 miles per gallon and the current cost of gasoline is $2.35, what will the gas for their trip cost?
a.$74.45
b.$58.75
c.$31.68
d.$66.75
Answers
Answer: a. $74.45
Step-by-step explanation: good luck
Find the values of g and k.
14°
hᵒ gº
131°
jº
125°
mº

Answers
Answer:
g° = 49°k° = 76°Step-by-step explanation:
You want the measures of angles 'g' and 'k' as marked in the diagram.
Angle relationsThe relevant angle relations here are ...
angles of a linear pair are supplementaryinterior angles of a triangle total 180°vertical angles are congruentAngle gAngle g forms a linear pair with the one marked 131°. Its measure is ...
g° = 180° -131°
g° = 49°
Angle kAngle j° is a vertical angle with respect to angle g°, so has the same measure: 49°.
Together, angles j°, k°, m° total 180°. We also know that m° and the angle marked 125° are a linear pair, so total 180°
j° +k° +m° = 180° = 125° +m°
j° +k° = 125° . . . . . . . subtract m°
k° = 125° -j° = 125° -49°
k° = 76°
__
Additional comment
You will notice we did not need to know the value of m° in order to find k°. The relation between 125° and the sum f° and k° is described by "an exterior angle to a triangle is equal to the sum of the remote interior angles." Knowing this relation can save a bit of work, as it does here.
You may notice, too, that k° is the difference between the sum of 131° and 125°, and 180°: k° = 131° +125° -180° = 76°.
Other angles are ...
h° = 131° -14° = 117°m° = 180° -125° = 55°j° = g° = 49°The angles in parallel lines are solved and the values of g and k are
g = 49° and k = 76°
Given data ,
Let the measure of angle ∠g = ∠g
Let the measure of ∠k = ∠k
Now , the measure of ∠m = 180° - 125° ( adjacent angles = 180° )
So , the measure of ∠m = 55°
Now , the measure of ∠g = 180° - 131° ( adjacent angles = 180° )
So , the measure of ∠g = 49°
And , the measure of ∠j = measure of ∠g ( opposite angles are congruent )
So , the measure of ∠j = 49°
And , in triangle , ∠j + ∠m + ∠k = 180°
So , the measure of ∠k = 180° - ( 49° + 55° )
The measure of ∠k = 76°
Hence , the measure of angles are ∠g = 49° and ∠k = 76°
To learn more about angles in parallel lines click :
https://brainly.com/question/27400033
#SPJ1
Find the volume of the solid formed by rotating the region inside the first quadrant enclosed by y=x^2,y=5x about the x-axis.
Answers
The volume of the solid formed by rotating the region inside the first quadrant enclosed by the curves y = x and y = 5x about the x-axis is (250π/7) cubic units. When finding the volume of a solid of revolution, we use the method of cylindrical shells.
To calculate the volume, we integrate the area of each cylindrical shell formed by rotating an infinitesimally small strip about the x-axis. The height of each shell is the difference between the y-values of the two curves, which is (5x - x²). The circumference of each shell is given by 2πx, and the thickness is dx. Therefore, the volume of each shell is 2πx(5x - x²)dx.
To find the total volume, we integrate this expression over the interval where the two curves intersect. Setting\(y = x^2\)and y = 5x equal to each other, we get x² = 5x. Solving this equation, we find two intersection points: x = 0 and x = 5. Thus, the limits of integration are from 0 to 5.
Integrating the expression \(2\pi x(5x - x^2)dx\) from 0 to 5 gives us the volume of the solid formed by rotating the region inside the first quadrant. Evaluating this integral, we find the volume to be (250π/7) cubic units.
Learn more about area here: https://brainly.com/question/1631786
#SPJ11
please answer both questions and give me the step by step instructions for these problems.

Answers
The simplified form of the expressions are 69-y/16 and -x/3 - 27 respectively
Solving algebraic equationAn algebraic equation can be defined as a mathematical statement in which two expressions are set equal to each other.
Given the following algebras
5-y/16 + 4
Find the LCM
5-y+4(16)/16
5-y+64/16
69-y/16
Hence the simplified form of the equation is 69-y/16
For the algebraic equation -3(x/8 + 9)
Expand
-3(x/8) + -3(9)
-3x/9 - 27
-x/3 - 27
Hence the simplified form of the expression is -x/3 - 27
Learn more on algebra here: https://brainly.com/question/25976025
#SPJ1
Find the initial value, final value, and initial slope when this system is subjected to a unit step input, u(t) = 1(t).
Answers
- The initial value is 0 since the system is at rest , the final value is 1 after the input is applied, the initial slope is undefined as there is an instantaneous change from 0 to 1 at t = 0.
The initial value refers to the value of the system at time t = 0. It represents the system's behavior before the unit step input is applied. In this case, since the system is subjected to a unit step input u(t) = 1(t), which means it jumps from 0 to 1 at t = 0, the initial value is 0.
The final value refers to the value of the system at a very large time, approaching infinity. It represents the steady-state behavior of the system after it has settled down. In this case, when the unit step input is applied, the system reaches a final value of 1, as it stays at that value indefinitely.
The initial slope refers to the rate of change of the system at t = 0. It represents how the system responds to the sudden change in input. In this case, since the unit step input causes an immediate jump from 0 to 1, the initial slope is undefined. This is because the system experiences an instantaneous change and there is no slope to describe the behavior at t = 0.
Learn more about slope from the following link:
https://brainly.com/question/10155554
#SPJ11
The given system is subjected to a unit step input, u(t) = 1(t). To find the initial value, final value, and initial slope, we need to analyze the system's response over time.
1. Initial value: The initial value of the system is the output value at t = 0. To find it, we evaluate the output of the system when the input is u(t) = 1(t) at t = 0.
2. Final value: The final value of the system is the output value as time approaches infinity. In this case, as the unit step input u(t) = 1(t) remains constant after t = 0, the system will eventually settle into a steady-state response. We can find the final value by evaluating the output at a sufficiently large time.
3. Initial slope: The initial slope is the derivative of the output with respect to time at t = 0. We can find it by taking the derivative of the system's response equation with respect to time and evaluating it at t = 0.
Remember that the specific system's response equation and properties are needed to provide a more accurate analysis.
Learn more about infinity from the following link:
https://brainly.in/question/679559
#SPJ11
Which polyhedra (regular or irregular) have perfect symmetry (plane of symmetry and rotation of symmetry) and why ?
Answers
Answer:
regular
Step-by-step explanation:
because an irregular polyhedron is formed by polygons of different shapes where all the components are not the same.
Evaluate the limit. Justify your response. A. lims→1 s3−1/s−1 B. limx→1 x2+4x−5/x−1 C. limx→144 x−12/x−144.
Answers
The limit of a function can be found using several methods depending on the form of the given function. To evaluate the given limit, we can use the limit formulas or L'Hôpital's rule where necessary.
(a) lims→1 (s³ - 1) / (s - 1) = 3:
To evaluate this limit, we can factorize the numerator as a difference of cubes:
s³ - 1 = (s - 1)(s² + s + 1)
Now, we can cancel out the common factor (s - 1) from the numerator and denominator:
lims→1 (s³ - 1) / (s - 1) = lims→1 (s² + s + 1)
Plugging in s = 1 into the simplified expression:
lims→1 (s² + s + 1) = 1² + 1 + 1 = 3
Therefore, the correct value of the limit lims→1 (s³ - 1) / (s - 1) is indeed 3.
(b) limx→1 (x² + 4x - 5) / (x - 1) = 10:
To evaluate this limit, we can apply direct substitution by substituting x = 1:
limx→1 (x² + 4x - 5) / (x - 1) = (1^2 + 4(1) - 5) / (1 - 1) = 0 / 0
Since direct substitution yields an indeterminate form of 0/0, we can apply L'Hôpital's rule:
Differentiating the numerator and denominator:
limx→1 (x² + 4x - 5) / (x - 1) = limx→1 (2x + 4) / 1 = 2(1) + 4 = 6
Therefore, the correct value of the limit limx→1 (x² + 4x - 5) / (x - 1) is 6.
(c) limx→144 (x - 12) / (x - 144) = -1/156:
To evaluate this limit, we can apply direct substitution by substituting x = 144:
limx→144 (x - 12) / (x - 144) = (144 - 12) / (144 - 144) = 132 / 0
Since the denominator approaches 0 and the numerator is non-zero, the limit diverges to either positive or negative infinity depending on the direction of approach. In this case, we have a one-sided limit:
limx→144+ (x - 12) / (x - 144) = +∞ (approaches positive infinity)
limx→144- (x - 12) / (x - 144) = -∞ (approaches negative infinity)
Therefore, the correct value of the limit limx→144 (x - 12) / (x - 144) does not exist. It diverges to infinity.
To know more about limit visit:
https://brainly.com/question/12207558
#SPJ11
If f(x) = 4x2 and g(x) = x+1, find (f•g)(x)
A. 4x3+4x2
B. 4x(x)
C. 4X2 + 1
D. 4(x + 1)
Answers
Answer:
4x^3+4x^2
Step-by-step explanation:
f(x) = 4x^2
g(x) = x+1
(f•g)(x) = (4x^2) *(x+1) = 4x^3+4x^2
Plz only find the shaded area only I would appreciate if you did this on paper and showed all steps

Answers
If you already know |a_N| and |v|, then the formula a_N = k|v|^2 gives a convenient way to find the curvature. Use it to find the curvature and radius of curvature of the curve r(t) = (cos t +1 sin t) i + (sin t -t cos t) j, t > 0. The curvature is . The radius of curvature is .
Answers
The curvature of the curve r(t) is \(\sqrt( 5 + 2t cos t + t^2 ) / (2 + t^2)^{(3/2)}\), and the radius of curvature is \((2 + t^2)^{(3/2)} / \sqrt( 5 + 2t cos t + t^2 ).\)
How to find the curvature and radius of curvature of the curve?To find the curvature and radius of curvature of the curve r(t) = (cos t + sin t) i + (sin t - t cos t) j, t > 0, we need to compute the first and second derivatives of the curve:
r(t) = (cos t + sin t) i + (sin t - t cos t) j
r'(t) = (-sin t + cos t) i + (cos t + t sin t) j
r''(t) = (-cos t - sin t) i + (2cos t + t cos t - sin t) j
The magnitude of the vector r'(t) is:
\(| r'(t) | = \sqrt( (-sin t + cos t)^2 + (cos t + t sin t)^2 )= \sqrt( 2 + t^2 )\)
The curvature k is given by:
\(k = | r''(t) | / | r'(t) |^3\)
Substituting the expressions for r'(t) and r''(t), we get:
\(k = | r''(t) | / | r'(t) |^3\)
\(= | (-cos t - sin t) i + (2cos t + t cos t - sin t) j | / (2 + t^2)^{(3/2)}\)
\(= \sqrt( (cos t + sin t)^2 + (2cos t + t cos t - sin t)^2 ) / (2 + t^2)^{(3/2)}\)
Simplifying this expression, we get:
\(k = \sqrt( 5 + 2t cos t + t^2 ) / (2 + t^2)^{(3/2)}\)
To find the radius of curvature R, we use the formula:
R = 1 / k
Substituting the expression for k, we get:
\(R = (2 + t^2)^{(3/2)} / \sqrt( 5 + 2t cos t + t^2 )\)
Therefore, the curvature of the curve r(t) is \(\sqrt( 5 + 2t cos t + t^2 ) / (2 + t^2)^{(3/2)}\), and the radius of curvature is \((2 + t^2)^{(3/2)} / \sqrt( 5 + 2t cos t + t^2 ).\)
Learn more about radius of curvature of curve
brainly.com/question/31403088
#SPJ11
Suppose the random variables x,y, and z have joint distribution as follows xy^2z /180 , x-1, 2, 3; У-1, 2; z-1, 2, 3
Find the marginal distribution fi.3(2,3) (round off to third decimal place) of x and z.
Answers
The marginal distribution f(x,3)(2,3) of the random variables x and z
is approximately 0.167.
we first need to compute the marginal distribution f(x,z) by summing over all possible values of y. The given joint distribution function is
\( f(x,y,z) = xy^2z / 180.\)
To compute f(x,z), we sum over all possible values of y:
\(f(x,z) = Σ [f(x,y,z)]\) for all values of y.
For the given values of x = 2 and z = 3:
\(f(2,3) = Σ [f(2,y,3)]\) for y = 1, 2.
\(f(2,3) = f(2,1,3) + f(2,2,3).\)
Now, we'll compute the joint distribution values:
\(f(2,1,3) = (2 * 1^2 * 3) / 180 = 6 / 180.\)
\(f(2,2,3) = (2 * 2^2 * 3) / 180 = 24 / 180.\)
Then, sum the values:
\(f(2,3) = (6 / 180) + (24 / 180) = 30 / 180.\)
Now, we'll round off to the third decimal place:
\(f(2,3) ≈ 0.167\) (rounded to three decimal places).
So, the marginal distribution f(x,3)(2,3) of x and z is approximately 0.167.
for such more questions on marginal distribution
https://brainly.com/question/30438396
#SPJ11
The bearing of point Y from point X is 065°.
The bearing of point Z from point Y is 145º.
The bearing of point Z from point X is 105º.
Find the bearing of point X from point Z.
Answers
Answer:
285°
Step-by-step explanation:
You have probably learned bearing in geography and maybe even mathematics.
First off, skip the Y part since the answer you're looking for have nothing to do with it.
So, 180°+105°=285°
Those red-colored angles.. they have the same angle.
That's cause they're alternate angles and alternate angle are equal.
That arrow-like thing is to proove that they're parallel.

which of the following basic functions is equivalent to the piecewise-defined function f(x)= x if x≥0 −x if x<0 ? question content area bottom part 1 a. f(x)= 1 x b. f(x)=x c. f(x)=x2 d.
Answers
The basic function equivalent to the piecewise-defined function f(x) = x if x ≥ 0 and -x if x < 0 is f(x) = |x|, which represents the absolute value of x.
The given piecewise-defined function f(x) has different expressions for different intervals. For x greater than or equal to zero, f(x) takes the value of x. For x less than zero, f(x) is equal to -x. We need to find a basic function that captures this behavior.
Among the options provided, f(x) = |x| is equivalent to the given piecewise function. The absolute value function, denoted by |x|, returns the positive value of x regardless of its sign. When x is non-negative, |x| equals x, and when x is negative, |x| is equal to -x, mirroring the conditions of the piecewise-defined function.
The function f(x) = |x| represents the absolute value of x and matches the behavior of the given piecewise-defined function, making it the equivalent basic function.
In summary, the basic function equivalent to the piecewise-defined function f(x) = x if x ≥ 0 and -x if x < 0 is f(x) = |x|, which represents the absolute value of x.
Learn more about absolute value here:
https://brainly.com/question/17360689
#SPJ11
Solve the given equation
x – 1 + 5x = 23
Answers
Step-by-step explanation:
x - 1 + 5x = 23
6x - 1 = 23
6x = 23 + 1 = 24
6x = 24
x = 24/6
x = 4 ans.
HOPE THIS ANSWER HELPS YOU DEAR! TAKE CARE.
Ralph has 3/4 gallons of paint. He wants to store all of the paint equally among 5 containers. How much paint, in gallons, will Ralph store in each container?
Answers
Ralph will store 3/20 gallons of paint in each container.
Explain gallons
Gallons are a unit of measurement commonly used for liquids, especially in the United States. One gallon is equal to 128 fluid ounces or approximately 3.785 liters. It is used to measure the volume of liquids such as gasoline, milk, and water, and is often used in cooking, construction, and manufacturing industries.
According to the given information
To divide 3/4 gallons of paint equally among 5 containers, we need to perform the division (3/4)/5:
(3/4)/5 = 3/4 × 1/5 = 3/20
Therefore, Ralph will store 3/20 gallons of paint in each container.
To know more about gallons visit
brainly.com/question/19638640
#SPJ1
Answer:
Step-by-step explanation
To find the answer you would have to divide 3/4 gallons of paint equally among 5 containers, we need to perform the division (3/4)/5:
(3/4)/5 = 3/4 × 1/5 = 3/20
Ralph will store 3/20 gallons of paint in each container.
Consider a Brownian motion W(t) with t ≥ 0 and consider two stock prices de-
scribed by S 1(t) and S 2(t) which fulfill the following stochastic differential equations
(SDEs)
dS 1(t) =μ1S 1(t)dt +σ1S 1(t)dW(t)
dS 2(t) =μ2S 2(t)dt +σ2S 2(t)dW(t),
with μ1, μ2 ∈Rand σ2 > σ1 > 0.
a) For f (x) =log x, derive the SDE satisfied by the process f (S 1(t)).
b) Without further calculation, what is the process followed by f (S 2(t))?
c) Find the SDE satisfied by Y(t) =g(S 1(t),S 2(t)) =ln(S 1(t)/S 2(t)) when μ =
μ1 =μ2. What type of stochastic process is Y(t) undergoing? Describe the
parameters of this process.
Answers
The SDE satisfied by the process f (S 1(t)) is μ1dt + σ1dW(t). The process followed by f(S2(t)) is (μ2/S2(t))dt + (σ2/S2(t))dW(t). The SDE satisfied by Y(t) is (μ1- μ2)dt + (σ1^2 + σ2^2) / 2 dW(t). The stochastic process Y(t) is an Ornstein-Uhlenbeck process. The parameters of this process are as follows: Mean = 0, Variance = (σ1^2 + σ2^2) / 2, Reversion rate = μ1 - μ2
a) For f (x) = log x, the SDE satisfied by the process f(S1(t)) is obtained as follows: df(S1(t)) = df(S1(t)) / dS1(t) × dS1(t)
In the given problem, f (S1(t)) = log(S1(t)).
Thus, df(S1(t)) = (1/S1(t)) × dS1(t)
Substituting S1(t) in the given SDEs, we get
dS1(t) = μ1S1(t)dt + σ1S1(t)dW(t)
Substituting the value of dS1(t) in df(S1(t)), we get
df(S1(t)) = (1/S1(t)) × (μ1S1(t)dt + σ1S1(t)dW(t))
Simplifying the above equation, we get
df(S1(t)) = (μ1dt + σ1dW(t))
b) The process followed by f(S2(t)) can be obtained as follows:
f(S2(t)) = log(S2(t))d[f(S2(t))] = d[log(S2(t))]d[f(S2(t))] = (1/S2(t))dS2(t)
Substituting the value of dS2(t) in the above equation, we get
d[f(S2(t))] = (μ2/S2(t))dt + (σ2/S2(t))dW(t).
Thus, the process followed by f(S2(t)) is given by
d[f(S2(t))] = (μ2/S2(t))dt + (σ2/S2(t))dW(t)
c) The SDE satisfied by Y(t) = g(S1(t),S2(t)) = ln(S1(t)/S2(t)) when μ = μ1 = μ2 is obtained as follows:
Given: dS1(t) = μS1(t)dt + σ1S1(t)dW(t)
dS2(t) = μS2(t)dt + σ2S2(t)dW(t)
Therefore, ln(S1(t)/S2(t)) can be rewritten as ln(S1(t)) - ln(S2(t)).
Substituting the values of dS1(t) and dS2(t), we get
d(ln(S1(t)/S2(t))) = (μ1- μ2)dt + (σ1^2 + σ2^2) / 2 dW(t)
The stochastic process Y(t) is an Ornstein-Uhlenbeck process. The parameters of this process are as follows: Mean = 0, Variance = (σ1^2 + σ2^2) / 2, Reversion rate = μ1 - μ2
To know more about stochastic process, click here:
https://brainly.com/question/30407952
#SPJ11
What are two numbers that when multiplied equal -30 and when added together equal 1?
Answers
Answer:
5 and 6
Step-by-step explanation:
-5 x 6 = -30
-5 + (6) = 1
x2 + 1x - 30 = 0
(X - 5 ) (X + 6)
To summarize, since -5 and 6 multiply to -30 and add up 1, you know that the following is true:
x2 + 1x - 30 = (X - 5 ) (X + 6)
Find the slope intercept of (2,-2) and (3,2)
Answers
Answer:
slope = y'-y/x' - x
= 2-(-2)/3-2
=2+2 /1
=4
slope = 4
P(4,6), over the x-axis
Answers
The image of point P(4,6) after a reflection over the x-axis is given as follows:
P'(4,-6).
How to obtain the image of point P?The coordinates of the point P in this problem are given as follows:
P(4,6).
Meaning that:
The x-coordinate is of 4.The y-coordinate is of 6.The rule for a reflection over the x-axis is given as follows:
(x,y) -> (x,-y).
Meaning that the x-coordinate remains constant, while the y-coordinate has the signal exchanged.
Applying the rule, the coordinates of the image are given as follows:
x-coordinate of 4, as it remains constant.y-coordinate of -6, as the signal is exchanged.Then the coordinates of the image after the reflection are given as follows:
P'(4,-6).
More can be learned about reflections over the x-axis at brainly.com/question/21603787
#SPJ1
The quadratic function f(x) has roots of 4 and −6, and it passes through the point (1, 21). What is the vertex form of the equation of f(x)?
Answers
\(f\left(x\right)=-1\left(x+1\right)^{2}+25\)
If you need to do functions like this use desmos graphing calculator.
In the figure, RV, WS, and QT intersect at point P.
What is the value of x? Show your work.
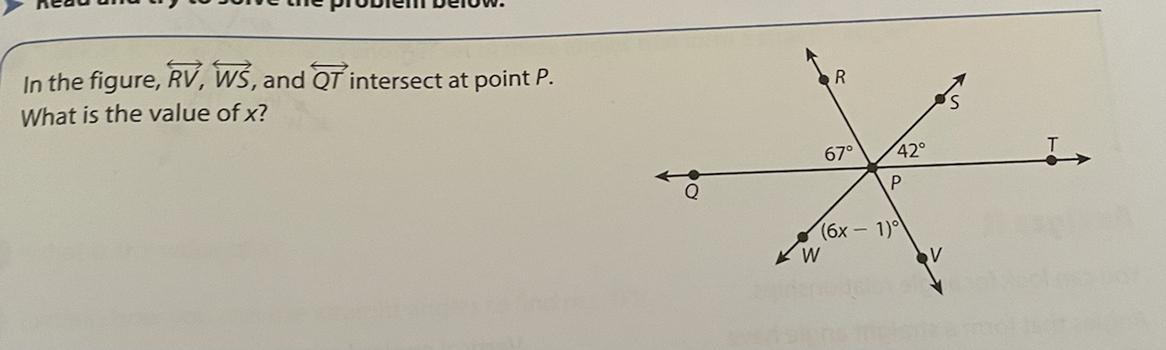
Answers
Answer:
x = 12
Step-by-step explanation:
67+42+6x-1=180
108+6x=180
6x=72
x=12
The triangle has an area of 7 7/8 cm2 and a base of 5 1/4 cm. What is the height?
Answers
Answer:
3
Step-by-step explanation:
7 7/8÷51/4
3/2÷1/2
3
A=bh1/2
A=5 1/4×3×1/2
A=15 3/4×1/2
A= 7 7/8
(Mark as brainliest please)
A train leaves at 5.35 and arrives at 18.20 how long its journey . how long is the journey
Answers
Answer:
13 hours 55 minutes
Step-by-step explanation:
A train leaves at 5:35
The train arrives at its destination at 18:20
Therefore the time interval between 5:35 and 18:20 is
13 hours 55 minutes
Hence the journey is 13 hours 55 minutes long
An object travels along a circular path so that it completes one revolution in 8 seconds. If the linear velocity of the object is 90.7 inches per minute, what is the diameter in inches, of the circular path?
Answers
Answer:
try 90 decided by 8 maybe that'll help