finding the distance between two points (-4,-3),(6,1)
Answers
Answer:
it's the first one
Step-by-step explanation:
Related Questions
у
4
3
2
1
1
-4 -3 -2 -1
1
1
2 3 4
-1
-2 -3
-4
What is the slope of the line?

Answers
Answer-
y=-2x+2
It starts at +2 so that is the b
And -2x is how you move so that is the m
That's how I was taught and how I remember it lol hope it helped ik it wasn't the best its 12 am here soo I be tired
47/ 15 decimal rounded to the nearest hundred
Answers
Answer:
4
Step-by-step explanation:
it would be 4 because 47/15 = 3.23333 and because you said to the nearest hundred than it would be rounded to 4
The hourly wage increase each employee receives each year depends on their number of years of service. Every three years of service means an increase of $0.50 per hour. So, employees that have been with the company for less than three years can expect to receive an increase of $0.50 per hour. Employees that have been with the company for at least three years, but less than six years can expect an increase of $1.00. Employees that have been with the company for at six years, but less than nine years, receive an increase of $1.50 per hour. And, employees of at least nine years, but less than twelve years receive an increase of $2.00. Write a function to represent this scenario. Which graph represents this wage increase for x < 12?

Answers
The solution is Option C.
The graph which represents the inequality equation is
f ( x ) = { 0.50 , if x < 3
1 , if 3 ≤ x < 6
1.50 , if 6 ≤ x < 9
2.00 , if 9 ≤ x < 12 }
What is an Inequality Equation?
Inequalities are the mathematical expressions in which both sides are not equal. In inequality, unlike in equations, we compare two values. The equal sign in between is replaced by less than (or less than or equal to), greater than (or greater than or equal to), or not equal to sign.
In an inequality, the two expressions are not necessarily equal which is indicated by the symbols: >, <, ≤ or ≥.
Given data ,
Let the number of years be = x
Let the increment in wages be = y
Now , the equation will be
For the employees that have been with the company for less than three years can expect to receive an increase of $0.50 per hour
So , the inequality equation is x < 3 , f ( x ) = 0.50
Employees that have been with the company for at least three years, but less than six years can expect an increase of $1.00
So , the inequality equation is 3 ≤ x < 6 , f ( x ) = 1
Employees that have been with the company for at six years, but less than nine years, receive an increase of $1.50 per hour
So , the inequality equation is 6 ≤ x < 9 , f ( x ) = 1.50
Employees of at least nine years, but less than twelve years receive an increase of $2.00
So , the inequality equation is 9 ≤ x < 12 , f ( x ) = 2
Therefore , the graph which represents the solution is Option C.
Hence , the inequality equation is 9 ≤ x < 12 , f ( x ) = 2
To learn more about inequality equations click :
https://brainly.com/question/11897796
#SPJ2
For a luncheon, Andre made 5 cups of tuna salad, 2 cups of chicken salad, and 3 cups of egg salad. What is the total number of servings Andre made for all three types of salad?

Answers
Answer:
27 servings
Step-by-step explanation:
You must calculate the number of servings for each type of food and then add them. To calculate the number of servings, divide the amount of each food by the size of its serving.
Tuna: 5 / 1/2 = 5 * 2 = 10 servings
Chicken Salad: 2 / 1/4 = 2 * 4 = 8 servings
Egg salad: 3 / 1/3 = 3 * 3 = 9 servings
Total number of servings = 10 + 8 + 9 = 27
Answer: 27 servings
If two methods agree perfectly in a method comparison study, the slope equals ________ and the y-intercept equals ________.
a. 0.0, 1.0
b. 1.0, 0.0
c. 1.0, 1.0
d. 0.0, 0.0
e. 0.5, 0.5
Answers
If two methods agree perfectly in a method comparison study, the slope equals 1.0 and the y-intercept equals 0.0. Therefore, option (b) is the correct answer.
In a method comparison study, the goal is to compare the agreement between two different measurement methods or instruments. The relationship between the measurements obtained from the two methods can be described by a linear equation of the form y = mx + b, where y represents the measurements from one method, x represents the measurements from the other method, m represents the slope, and b represents the y-intercept.
When the two methods agree perfectly, it means that there is a one-to-one relationship between the measurements obtained from each method. In other words, for every x value, the corresponding y value is the same. This indicates that the slope of the line connecting the measurements is 1.0, reflecting a direct proportional relationship.
Additionally, when the two methods agree perfectly, there is no systematic difference or offset between the measurements. This means that the line connecting the measurements intersects the y-axis at 0.0, indicating that the y-intercept is 0.0.
Therefore, in a perfect agreement scenario, the slope equals 1.0 and the y-intercept equals 0.0, which corresponds to option (b).
Learn more about y-intercept here:
https://brainly.com/question/14180189
#SPJ11
James takes out a loan of 9000 euros which keeps on charging simple interest at a rate of 3% of the original amount per annum until it is cleared. James pays of 770 euros each year to reduce the loan. After how many years will James have fully cleared the loan?
Answers
James will fully clear the loan after approximately 12 years when the remaining balance reaches zero.
To determine the number of years it will take for James to fully clear the loan, we need to calculate the remaining balance after each payment and divide the initial loan amount by the annual payment until the remaining balance reaches zero.
The loan amount is 9000 euros, and James pays off 770 euros each year. Since the interest is charged at a rate of 3% of the original amount per annum, the interest for each year will be \(0.03 \times 9000 = 270\) euros.
In the first year, James pays off 770 euros, and the interest on the remaining balance of 9000 - 770 = 8230 euros is \(8230 \times 0.03 = 246.9\)euros. Therefore, the remaining balance after the first year is 8230 + 246.9 = 8476.9 euros.
In the second year, James again pays off 770 euros, and the interest on the remaining balance of 8476.9 - 770 = 7706.9 euros is \(7706.9 \times 0.03 = 231.21\) euros. The remaining balance after the second year is 7706.9 + 231.21 = 7938.11 euros.
This process continues until the remaining balance reaches zero. We can set up the equation \((9000 - x) + 0.03 \times (9000 - x) = x\), where x represents the remaining balance.
Simplifying the equation, we get 9000 - x + 270 - 0.03x = x.
Combining like terms, we have 9000 + 270 = 1.04x.
Solving for x, we find x = 9270 / 1.04 = 8913.46 euros.
For more such questions on loan
https://brainly.com/question/25696681
#SPJ8
a bakery uses 8 tablespoons of honey for every 10 cups of flour so how many tablespoons of honey do they use with 20 cups of flour
Answers
a bakery uses 8 tablespoons of honey for every 10 cups of flour so how many tablespoons of honey do they use with 20 cups of flour
we can use a rule of three
Step 1
define
\(\begin{gathered} 8\text{ tablespoons of honey}\rightarrow10\text{ cups of flour} \\ x\text{ tablespoons of honey}\rightarrow20\text{ cups of flour} \end{gathered}\)there is a relation between the honey and the flour, is needs to be constant, so
Step 2
fin the ratio
\(\begin{gathered} \frac{8}{10}=\frac{x}{20} \\ \end{gathered}\)Now
Step 3
solve for x
\(\begin{gathered} \frac{8}{10}=\frac{x}{20} \\ x=\frac{8\cdot20}{10} \\ x=\frac{160}{10} \\ x=16 \end{gathered}\)so, he uses 16 tablespoons
I need help asap please


Answers
Answer:
56π
Step-by-step explanation:
1. Approach
To find the radius of a circle, use the formula;
\(A = r^{2}\)π
To find the area of the shaded region, find the area of the larger circle, and then subtract the area of the smaller circle from it.
It is given that the larger circle has a radius of 9, and the smaller has a radius of 5.
2. Area of the larger circle
\(A = r^{2}\)π
Substitute in known value (use 3.14 for π)
\(A = (9)^{2} * 3.14\)
A = 254.47
3. Area of the smaller circle
\(A = r^{2}\)π
Substitute in known value (use 3.14 for π)
\(A = (5)^{2} * 3.14\)
A = 78.54
4. Area of the shaded region
Subtract the area of the smaller circle from the area of the larger circle;
254.47 - 78.54 = 175.93
~ 56π
Does anyone know this answer??

Answers
Answer:
Option (4)
Step-by-step explanation:
Equation of a line passing through a point \((x_1,y_1)\) and with slope 'm' is,
y - y₁ = m(x - x₁)
Given → Slope 'm' = -2
Point through which the line is passing is (-1, -2)
x₁ = -1 and y₁ = -2
Therefore, equation will be,
y + 2 = -2(x + 1)
y = -2x - 2 - 2
y = -2x - 4
Option (4) is the correct option.
Write the equation of the line that passes through the points (3,5) and (6,7). Put your answer in fully simplified point-slope form, unless it is a vertical or horizontal line.
Answers
Answer:
Below
Step-by-step explanation:
Slope = rise/run = 2/3
Point (3,5) y-5 = 2/3 (x-3)
y = 2/3x +3
The midpoint of GH is M(-5, 4). One endpoint is H (-8, 0).
Find the coordinates of end point G
Answers
Answer:
G (-2,8)
Step-by-step explanation:
(-8+x)/2 = -5
-8 + x = -10
x = -10 + 8
x = -2
(0+y)/2 = 4
y = 4 · 2
y = 8
can someone help me solve this?

Answers
The answer is B: 1/16
How do you solve the equation (5x/6)(5x/2) = 5^{16}
Answers
Answer:
Please check the answer if it is correct or not
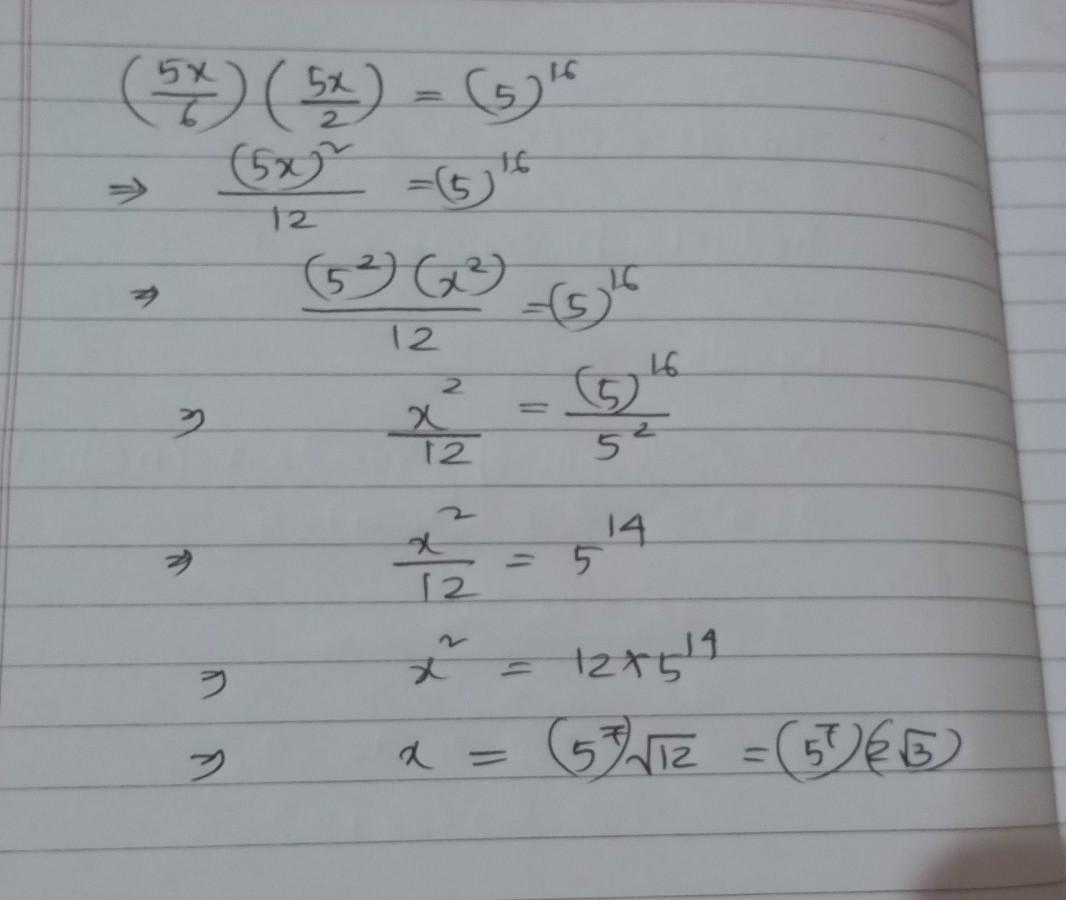
10. What is m/ABD in the figure shown?

Answers
The measure of m∠ABD in the figure shown is 19°.
Given:
∠BCD = 71°
In the figure, ΔABC is an isosceles triangle where AB = BC.
According to the Isosceles Triangle Theorem, an isosceles triangle has equal angles on either side of its equal sides.
So, ∠BAD = ∠BCD = 71°
The sum of angles in a triangle sums to 180°.
∠ABC + ∠BAD + ∠BCD = 180°
∠ABC + 71° + 71° = 180°
∠ABC + 142° = 180°
∠ABC = 180° - 142° = 38°
DB is the angle bisector of ∠ABC.
Now, ∠ABD = ∠CBD = 38°/2 = 19°
The measure of ∠ABD is 19°.
To know more about Isosceles triangle theorems visit:
https://brainly.com/question/12951731
#SPJ9
2
2 points
Solve for the indicated missing part. Round to 1 d.p.
1
Find mZA
с
2
3
54°
B
4
Answers
Step-by-step explanation:
a diagram is necessary. please provide a diagram.
If the consumption function for Australia in 2021 is given as = 0.0052 + 0.3 + 20 where: C = total consumption of Australia in the year 2021 Y = total income of Australia in the year 2021 Calculate the marginal propensities to consume (MPC = ) and save when Y = 10. Assume that Australians cannot borrow, therefore total consumption + total savings = total income. Expert Answer
Answers
The marginal propensity to consume (MPC) for Australia in 2021, when total income (Y) is 10, is 0.3.
The consumption function for Australia in 2021 is given as C = 0.0052 + 0.3Y + 20, where C represents the total consumption and Y represents the total income. To calculate the MPC, we need to determine how much of an increase in income is consumed rather than saved. In this case, when Y = 10, we substitute the value into the consumption function:
C = 0.0052 + 0.3(10) + 20
C = 0.0052 + 3 + 20
C = 23.0052
Next, we calculate the consumption when income increases by a small amount, let's say ΔY. So, when Y increases to Y + ΔY, the consumption function becomes:
C' = 0.0052 + 0.3(Y + ΔY) + 20
C' = 0.0052 + 0.3Y + 0.3ΔY + 20
To find the MPC, we subtract the initial consumption (C) from the new consumption (C') and divide it by the change in income (ΔY):
MPC = (C' - C) / ΔY
MPC = (0.0052 + 0.3Y + 0.3ΔY + 20 - 23.0052) / ΔY
Simplifying the equation, we can cancel out the terms that don't involve ΔY:
MPC = (0.3ΔY) / ΔY
MPC = 0.3
Learn more about Marginal propensity
brainly.com/question/32676784
#SPJ11
What is the result of 1.58/3.793 written with the correct number of significant figures?
A.) 0.41656
B.) 0.4166
C.) 0.417
D.) 0.42
E.) 0.4
Answers
Answer:C
Step-by-step explanation:
(-2 + 1)² + 5(12 3) - 9.
The value of the expression is ?
Answers
Answer:
The total value of the given expression is 12.
Step-by-step explanation:
(-2 + 1)² + 5(12 ÷ 3) - 9
First, do the expressions within the parentheses.
(-1)² + 5(4) - 9
Next, simplify the exponents.
1 + 5(4) - 9
Next, multiply 5 by 4.
1 + 20 - 9
Add 1 and 20 together.
21 - 9
Subtract 9 from 21.
12
So, the final answer to this equation is 12.
The simplification form of the number expression (-2 + 1)² + 5(12 : 3) - 9 is 12; the answer is 12.
What is an arithmetic operation?It is defined as the operation in which we do the addition of numbers, subtraction, multiplication, and division. It has a basic four operators that is +, -, ×, and ÷.
It is given that:
The number expression is:
= (-2 + 1)² + 5(12 : 3) - 9
The ratio can be described as the comparison of two quantities to determine how many times one obtains the other. The proportion can be expressed as a fraction or as a sign: between two integers.
= (-1)² + 5(12/3) - 9
= 1 + 5(4) - 9
= 1 + 20 - 9
= 21 - 9
= 12
Thus, the simplification form of the number expression (-2 + 1)² + 5(12 : 3) - 9 is 12; the answer is 12.
Learn more about the arithmetic operation here:
brainly.com/question/20595275
#SPJ2
A shipping crate is packed with unit cubes. The length of the crate is 4
units, the width is 2 units, and the height is 4 units. Find the volume
of the shipping crate.
Answers
Answer:
The volume of shipping crate is 32 unit cubes.
Step-by-step explanation:
Given that:
Length of the crate = 4 units
Width of the crate = 2 units
Height of the crate = 4 units
Volume of shipping crate = Length * Width * Height
Volume of the crate = 4 * 2 * 4
Volume of crate = 32 unit cubes.
Hence,
The volume of shipping crate is 32 unit cubes.
Answer:
32 units
Step-by-step explanation:
five soccer players each contributed and equal share toward a $50 gift for their coach. Write and solve an algebraic equation to find out how much each player paid.
Answers
Answer:$10 each
Step-by-step explanation: We can denote the amount each player pays by x. Since the amounts are equal, and there are 5 soccer players, the total is 5x. We are told that the total is 50, so 5x=50. Hence, x = $10. So each soccer player pays $10 each.
the test in an if function must evaluate to either a true or a false.
Answers
Yes, the test in an "if" function must evaluate to either a True or a False value.
An "if" function, also known as a conditional statement, is used to perform specific actions based on whether a certain condition is met or not. The test or condition within the "if" function needs to be evaluated as either True or False in order for the program to decide which action to execute. If the test evaluates to True, the program will perform the action within the "if" block, and if it evaluates to False, it will either execute the action in the "else" block (if present) or simply skip the "if" block.
When using an "if" function in programming, it is essential for the test or condition within the statement to result in a boolean value, which is either True or False. This is because the program needs to determine whether the condition is met or not, so it can decide which set of actions to execute. If the condition evaluates to True, the code within the "if" block will be executed, while if it evaluates to False, the code within the "else" block (if present) will be executed, or the "if" block will be skipped altogether.
To know more about function visit:-
https://brainly.com/question/30721594
#SPJ11
Will give Brainliest!
For a given input value q, the function g outputs a value r to satisfy the following equation.
−7q + 12r = 3q − 4r
Write a formula for g(q) in terms of q.
g(q) = ?
Answers
Answer:
The answer is 5/8q ... give me brainliest
The only way g(q) could be in terms of q will be eliminating r from the equation and that can be done by making r the subject ... which is what I did and the equation obtained from the left hand side becomes the function of g

Answer:
5/8q
Step-by-step explanation:
khan
Find the radius of the circle given by this equation:

Answers
Answer:
8
Step-by-step explanation:
We know that
Equation
\( {x}^{2} + {y}^{2} + 2gx + 2fy + c = 0\)
Represents the equation of Circle
where
\(radius = \sqrt{ {g}^{2} + {f}^{2} - c } \)
On comparing the given equation with general Equation of Circle
we get
\(g = - 5\)
\(f = 3\)
\(c = - 30\)
On substituting these values We get
\(radius = \sqrt{ { (- 5)}^{2} + {3}^{2} - ( - 30) } \)
\(radius = \sqrt{25 + 9 + 30 } = \sqrt{64 } = 8\)
\(radius = 8\)
In each bouquet of flowers, there are 5 roses and 8 white carnations. Complete the table to find
many roses and carnations there are in 5 bouquets of flowers.
There are (____) roses and (____) carnations in 5 bouquets

Answers
Answer:
25 roses and 40 white carnations
Step-by-step explanation:
Answer:
25 roses and 40 white carnations is the answer hope this helps:)
Step-by-step explanation:
Fill in the table (image provided)

Answers
Answer:
year 2 = 136
year 3 = 182
year 6 = 228
year 7 = 251
Answer & Explanation:
So the alien is 90 cm at birth. Your just going to add 23 for each year to the birth number of 90, because a year = 23 cm of growth
At 2 years it will be
90 + 23 + 23 = 136
At 4 years it will be
90 + 23 + 23 + 23 + 23 = 182
At 6 years it will be
23 x 6 = 138, 138 + 90 = 228
At 7 years it will be
23 x 7 = 161, 161 + 90 = 251
At a movie theater, the price of 2 adult tickets and 4 child tickets is 48$. The price of 5 adults and 2 child ticket is $64. What is the ticket price for one adult and for one child?
Answers
Answer:
$36
Step-by-step explanation:
$48 for 2 adults
Divide 48 by 2
24
So, $24 for 1 adult
$48 for 4 children
Divide 48 by 4
12
So $12 for 1 Child
Now add $24 and $12
$36
one child is 7$
10x2=20$
48$-20$=28$ 28$\4=7$
10$x5=50$
64$-50$=14$ 14$\2=7$
Out of many habits that Navdeep has resolved to change in himself, the most prominent is the habit of coming late in office. He carefully observed and found out that his probability of going by car A, B, C and D are 1/7. 3/7, 2/7 and 1/7 respectively. On further analysis, he figured out that his probability of getting late if he goes by car A, B, C and D are 8/9. 4/9. 5/9 and 4/9 respectively. On a particular day. he wants to go by car A. Can you tell us the probability of Navdeep travelling by car A, if he reaches office on time?
Answers
The probability of Navdeep traveling by car A if he reaches the office on time is 9/40.
According to the question:
Probability of Navdeep going by car A = 1/7
Probability of Navdeep going by car B = 3/7
Probability of Navdeep going by car C = 2/7
Probability of Navdeep going by car D = 1/7
Probability of Navdeep getting late if he goes by car A = 8/9
Probability of Navdeep getting late if he goes by car B = 4/9
Probability of Navdeep getting late if he goes by car C = 5/9
Probability of Navdeep getting late if he goes by car D = 4/9
Here, we are asked to find the probability of Navdeep traveling by car A, if he reaches the office on time. So, we can use Bayes’ theorem which is given as:
P(A|B) = (P(B|A) * P(A))/P(B)
Where,
P(A) = Probability of Navdeep going by car A = 1/7
P(B|A) = Probability of Navdeep reaching on time given he takes car A = 1 – P(getting late | A) = 1 – 8/9 = 1/9
P(B) = Probability of Navdeep reaching on time = P(B|A) * P(A) + P(B|B) * P(B) + P(B|C) * P(C) + P(B|D) * P(D)= (1 – 8/9) * 1/7 + (1 – 4/9) * 3/7 + (1 – 5/9) * 2/7 + (1 – 4/9) * 1/7= 1/63 + 5/21 – 10/63 + 5/63= 40/63
Putting these values in Bayes’ theorem we get:
P(A|B) = (P(B|A) * P(A))/P(B) = [(1/9) * (1/7)]/(40/63) = 9/40
Learn more about Bayes’ theorem:
https://brainly.com/question/14989160
#SPJ11
) Which expression is equivalent to
- 7?
(0+21) 10-2
(21)
(6+21)
(6 - 21)
3
Answers
look at the 2 boxes and the 4 probability histograms below. each box has 2 probability histograms associated with it. one is the probability histogram for the sum of 2 draws made at random with replacement and the other is the probability histogram for the sum of 20 draws made at random with replacement from the box.
Answers
Explaining a bar graph
A bar graph graphically displays information. It uses bars that extend to various heights to symbolize value. Bar graphs can be created using any of the following: vertical bars, horizontal bars, grouped bars (several bars that compare values in a category), and stacked bars (bars containing multiple types of information).
Two sketches are shown in Histogram I for Box A.
20 drawings from Box B are represented in Histogram II.
20 drawings from Box A are represented in Histogram III.
Two draws are shown in Histogram IV for Box B.
Learn more about bar graph
https://brainly.com/question/24741444
#SPJ4
A store sells paint sets. Each paint set cost the same amount. During a sale, the store reduces the price of each paint set by $1.35. Yuri spends $6.88 on 2 paints sets at the same price.
Answers
Answer:
4.79
Step-by-step explanation:
4.79 is reasonable for the problem
The price of one paint set before the sale is $4.79
We are expected to determine the price of one paint set before the sale.
From the information given:
Yuri spends $6.88 on = 2 paint set∴
The amount at which Yuri bought 1 paint set is:
\(\mathbf{= \dfrac{\$6.88}{2.0}}\)
= $3.44
Recall that during the sale, the store reduce the price of each paint set by $1.35
Therefore, the price of one paint set before the sale is = $3.44 + $1.35 = $4.79
Learn more about word problems here:
https://brainly.com/question/23542499?referrer=searchResults