Find these common multiple for five and nine
Answers
Answer: 45
Step-by-step explanation:
The LCM of 5 and 9 is 45. To find the least common multiple of 5 and 9, we need to find the multiples of 5 and 9 (multiples of 5 = 5, 10, 15, 20 . . . . 45; multiples of 9 = 9, 18, 27, 36 . . . . 45) and choose the smallest multiple that is exactly divisible by 5 and 9, i.e., 45.
Related Questions
In the adjoining figure, ABCD is an isosceles trapezium in which angle BCD= 2x and angle ABC=3x. Find all the angles of the trapezium.
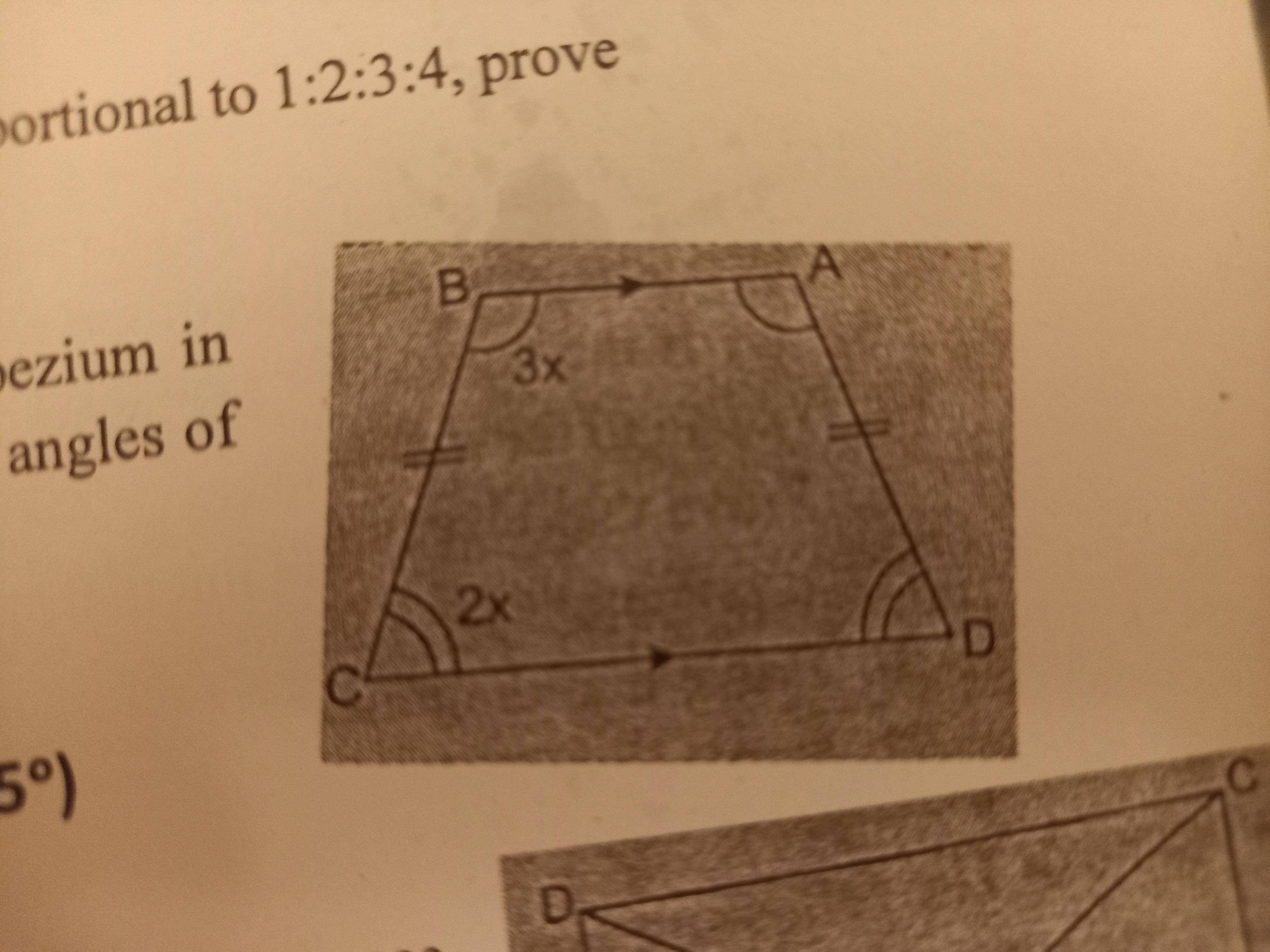
Answers
The trapezium is an isosceles trapezium. Then the measure of all angles will be 54°, 36°, 36°, and 54°.
What is a trapezium?It is a polygon that has four sides. The sum of the internal angle is 360 degrees. In a trapezium, one pair of opposite sides are parallel.
In the adjoining figure, ABCD is an isosceles trapezium in which angle ∠BCD = 2x and angle ∠ABC = 3x.
Then all the angles of the trapezium will be
Agngle ∠BCD = ∠ADC and angle ∠ABC = ∠BAD because the trapezium is an isosceles trapezium. Then we have
Then the value of x will be
∠ABC + ∠BCD + ∠CDA + ∠DAB = 180°
3x + 2x + 2x + 3x = 180°
10x = 180°
x = 18°
Then the measure of all angles will be
∠ABC = ∠BAD = 3x = 3 × 18 = 54°
∠BCD = ∠ADC = 2x = 2 × 18 = 36°
More about the trapezium link is given below.
https://brainly.com/question/22607187
#SPJ1
When Tyson opens and lays a cereal box out flat, he sees that the top and bottom of the box each measure 3 inches by 9 inches, the sides of the box each measure 3 inches by 13 inches, and the front and back of the box each measure 9 inches by 13 inches.
Please Answer with the work please.
Answers
Answer:
i
Step-by-step explanation:
Can someone explain by steps on how to do this

Answers
Answer:
8\(\sqrt{3}\)
Step-by-step explanation:
This is a special right triangle with angle measures 90-60-30 degrees
The side lengths are like the following :
The side length that sees 90 degrees is represented with x
The side length that sees 60 degrees is represented with x\(\sqrt{3}\)
The side length that sees 30 degrees is represented with 2x
the side that sees 90 degrees is given as 16 so x = 8 and so a = 8\(\sqrt{3}\)
The plant Mercury is about 57,900,000 kilometers from the sun. Pluto is about 1. 02 x 10^2 times farther away from the sn than Mercury. About how many kilometers is Pluto from the sun?
Answers
The distance between the Pluto and the sun is about 5,905,800,000 kilometers.
Distance between Mercury and the sun is = 57,900,000 kilometers.
The distance of Pluto from the sun
= Pluto is about 1.02 x 10^2 times farther away from the sun than Mercury.
⇒Distance of Pluto from the sun
= Distance of Mercury from the sun x 1.02 x 10^2
⇒Distance of Pluto from the sun = 57,900,000 km x 1.02 x 10^2
⇒Distance of Pluto from the sun = 57,900,000 km x 102
⇒ Distance of Pluto from the sun = 5,905,800,000 kilometers
Therefore, the distance of Pluto is about 5,905,800,000 kilometers away from the sun.
learn more about distance here
brainly.com/question/31530277
#SPJ4
5,5, 10, 10, 11, 12, 13, 13, 16, 16, 17, 18, 18
Min:
Q1:
Med:
13
Q3:
Max:
Answers
Answer:
5555555555555555555 i dont know what this maens sorry
A project has five activities with the durations (days) listed
below:
Activity
Precedes
Expected
Duration
Variance
Start
A, B
-
-
A
C
40
0.31
B
E
32
0.25
C
D
21
0.35
Answers
The critical path is the path with the longest duration, which in this case is A -> B -> D -> E with a duration of 11 days.
To determine the critical path of the project, we need to find the longest path of activities that must be completed in order to finish the project on time. This is done by calculating the earliest start time (ES) and earliest finish time (EF) for each activity.
Starting with activity A, ES = 0 and EF = 4. Activity B can start immediately after A is complete, so ES = 4 and EF = 7. Activity C can start after A is complete, so ES = 4 and EF = 6. Activity D can start after B is complete, so ES = 7 and EF = 9. Finally, activity E can start after C and D are complete, so ES = 9 and EF = 11.
The variance for each activity is also given, which allows us to calculate the standard deviation and determine the probability of completing the project on time. The critical path is the path with the longest duration, which in this case is A -> B -> D -> E with a duration of 11 days.
Using the expected durations and variances, we can calculate the standard deviation of the critical path. This information can be used to determine the probability of completing the project on time.
Know more about earliest start time here:
https://brainly.com/question/31043653
#SPJ11
Use the Multiplication Law of Exponents to explain why 5^3*5^-3 = 1
(URGENT PLEASE)
Answers
The multiplication law states that
a^m×a^n=a^m+nSo
5³×5-³=15^(3-3)=15⁰=11=1Answer:
1 = 1
Step-by-step explanation:
5^3*5^-3 = 1We all know the law of exponents,the one we'll use to solve this is the multiplication law:
x^y * x^z = x^y+zIf the bases are equal or two numbers then the powers are equal too.Solved:
\(5^3 \: * \: 5^{-3} = 1\)\(5 {}^{3 + ( - 3)} = 1\)\(5 ^{0} = 1\)x^0 = 1
\(1 = 1 \: ( \rm \: Proved)\)Alternate method:
5^3*5^-3 = 15^3*1/5^3 = 15^3 and 5^3 cancels, which results to
1 = 1HELP ME WITH THIS NOOW PLEASEEE

Answers
d...................................
Your colleague’s computer stops working, and no one from the IT department is available to fix it. You have basic knowledge of computer hardware. Which action should you take as an ethical employee?
A.
Initiate help by offering to check the computer.
B.
Start a conversation with your colleague and provide a distraction.
C.
Take a quick break and offer your computer for a short time.
D.
Ignore it because it is beyond your designated scope of work.
Answers
Since you have basic knowledge of computer hardware, an action which you should take as an ethical employee include the following: A. Initiate help by offering to check the computer.
What is a computer hardware?A computer hardware can be defined as a physical component of a computer system or an information technology (IT) that can be seen, touched and replaced.
In Computer technology, there are various examples of a computer hardware and these include the following:
Power supply unit (PSU).Hard-disk driveKeyboardMonitor (screen)MouseMotherboardCentral processing unit (CPU).Network interface card (NIC).Memory moduleBased on ethical principles, we can reasonably infer and logically conclude that an ethical employee should initiate help by offering to help check the colleague’s computer since he or she has basic knowledge of computer hardware.
Read more on computer hardware here: brainly.com/question/959479
#SPJ1
Which graph represents the function f {x} = -log (x-1) + 1?
Graph A
Graph B
Graph C
Graph D


Answers

Solve the proportion: 35/8 = 105/x
I will give brainiest if u friend me and dm for answers
Answers
Answer:
x=24
Step-by-step explanation:
35x = 105x8
35x=840
x=24
if the equation is 35/8 = 105/x= then your answer is x=24
-2 blank -8 <,>,=
Plsss?
Answers
Answer:
-2 > -8
Step-by-step explanation:
Since they are negative, -2 is greater than -8
Answer:
>
Step-by-step explanation:
Do remember the three symbols :
> - Greater than
< - Less than
= Equal to
An analogy you can use to always do this question is to think of the sign as a hungry alligator, and it wants to eat a bigger portion, so the opening of the teeth will revolt towards the bigger number. But there is a problem here, we're dealing with is negatives, it is the opposite than positives. The lower the number is in a negative is the bigger number in general, because it's closer to 0.
Therefore :
-2 > -8
a) 2x-4 =0
b) (x-1) (6-2x) =0
Answers
a) 2x - 4 = 0
2x = 4, x = 2
b) (x-1)(6-2x) = 0
If x-1 = 0
=> x = 0 + 1 = 1
If 6-2x = 0
=> 2x = 6-0 = 6
=> x = 3
\(\frac{3}{x+3} -\frac{4}{x-3}=\frac{5x}{x^{2} -9}\)
Answers
Answer:
Step-by-step explanation:
\(\frac{3}{x+3}-\frac{4}{x-3}=\frac{3*(x-3)}{(x+3)(x-3)}-\frac{4(x+3)}{(x-3)(x+3)}\\\\=\frac{3*x-3*3}{(x+3)(x-3)}-\frac{4*x+4*3}{(x+3)(x-3)}\\\\=\frac{3x-9}{x^{2}-3^{2}}-\frac{4x+12}{x^{2}-3^{2}}\\\\=\frac{3x - 9 -(4x + 12)}{x^{2}-3^{2}}\\\\=\frac{3x-9-4x-12}{x^{2}-9}\\\\=\frac{-x-21}{x^{2}-9}\\\\\)
\(\frac{3}{x+3}-\frac{4}{x-3}=\frac{5x}{x^{2}-9}\\\\\frac{-x-21}{x^{2}-9}=\frac{5x}{x^{2}-9}\\\\-x-21=\frac{5x}{(x^{2}-9)}*(x^{2}-9)\\\)
-x - 21 = 5x
Add 'x' to both sides
-x -21 +x = 5x + x
-21 = 6x
6x = -21
x = -21/6
= -7/2
x = -3.5
(-6, -2) and (5, 1) find the distance between these two points using the distance formula
(just trying to check my work because i did this question twice and one answer was 6 the other was 11.4)
Answers
Answer:
The answer is 11.401754
Answer: Approximately 11.4 units
================================================
Work Shown:
(x1,y1) is the first point (-6,-2)
(x2,y2) is the second point (5,1)
Apply the distance formula
\(d = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\\\\d = \sqrt{(-6-5)^2+(-2-1)^2}\\\\d = \sqrt{(-11)^2+(-3)^2}\\\\d = \sqrt{121+9}\\\\d = \sqrt{130}\\\\d \approx 11.4017542509913\\\\d \approx 11.4\\\\\)
The distance between the two points is roughly 11.4 units.
Which of the following polynomials has a remainder of -7 when divided by x – 2?
A. 4x3 + 2x2 + 5
B. x3 - 2x2 - 4x + 1
c. 3x² + 6x - 2
D.-2x3 + 4x2 + 3x - 2
Answers
Answer:
\(B.\ x^3 - 2x^2 - 4x + 1\)
Step-by-step explanation:
Given
Polynomials A to D
Divisor: x - 2
Required
Which of polynomial A - D has a remainder of -7
We start by equating the divisor to 0
\(x - 2 = 0\)
Make x the subject of formula
\(x = 2\)
Next is to substitute 2 for x in the polynomials to get the remainder;
\(A.\ 4x^3 + 2x^2 + 5\)
\(4(2)^3 + 2(2)^2 + 5\)
Open Brackets
\(4 * 8 + 2 * 4 + 5\)
\(32 + 8 + 5\)
\(Remainder = 45\)
\(B.\ x^3 - 2x^2 - 4x + 1\)
\((2)^3 - 2(2)^2 - 4(2) + 1\)
Open Brackets
\(8 - 2 * 4 - 4 * 2 + 1\)
\(8 - 8 - 8 + 1\)
\(Remainder = -7\)
\(C.\ 3x^2 + 6x - 2\)
\(3(2)^2 + 6(2) - 2\)
Open Brackets
\(3 * 4 + 6 * 2 - 2\)
\(12 + 12 - 2\)
\(Remainder = -2\)
\(D.\ -2x^3 + 4x^2 + 3x - 2\)
\(-2(2)^3 + 4(2)^2 + 3(2) - 2\)
Open Brackets
\(-2 * 8 + 4 * 4 + 3 * 2 - 2\)
\(-16 + 16 + 6 - 2\)
\(Remainder = 4\)
From the calculations above, the polynomial with a remainder of -7 when divided by \(x - 2\) is \(B.\ x^3 - 2x^2 - 4x + 1\)
The value of the polynomial \(x^3-2x^2-4x+1\) is -7 at x = 2. So, option B is correct.
Important information:
Remainder is -7.Divisor is \(x-2\).Remainder Theorem:According to the Remainder Theorem, if a polynomial is p(x) is divided by (x-c), then the remainder is p(c).
If polynomials have a remainder of -7 when divided by x – 2. So, the value of the polynomial must be -7 at x = 2.
Substitute x = 2 in the first polynomial.
\(4(2)^3+2(2)^2+5=45\neq -7\)
Substitute x = 2 in the second polynomial.
\((2)^3-2(2)^2-4(2)+1=-7\)
Substitute x = 2 in the third polynomial.
\(3(2)^2+6(2)-2=22\neq -7\)
Substitute x = 2 in the fourth polynomial.
\(-2(2)^3+4(2)^2+3(2)-2=4\neq -7\)
Only the value of the second polynomial is -7 at x = 2. Therefore, the correct option is B.
Find out more about 'Remainder Theorem' here:
https://brainly.com/question/4515216
Write the equation in slope-intercept from the two points given: (4,2) and (0,-5)
Explain. (step by step)
Answers
\((\stackrel{x_1}{4}~,~\stackrel{y_1}{2})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-5}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-5}-\stackrel{y1}{2}}}{\underset{run} {\underset{x_2}{0}-\underset{x_1}{4}}}\implies \cfrac{-7}{-4}\implies \cfrac{7}{4}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{2}=\stackrel{m}{\cfrac{7}{4}}(x-\stackrel{x_1}{4}) \\\\\\ y-2=\cfrac{7}{4}x-7\implies y=\cfrac{7}{4}x-5\)
-7/-4=7/4= m=1.75
Y=1.75x-5
60 apples are shared between abbie betty and carol in the ratios 1:3:x, where x>3. The number of apples in carols share is 18 more than the number of apples in bettys share. Find x
Answers
The value of x that satisfies the given conditions is 6. Let's solve the problem step by step.
We are given that the apples are shared in the ratios 1:3:x, where x > 3. This means that the total number of parts in the ratio is 1 + 3 + x = 4 + x.
To find the number of apples in each person's share, we divide the total number of apples (60) by the total number of parts in the ratio (4 + x):
Number of apples in each part = Total number of apples / Total number of parts
= 60 / (4 + x)
Now, we are given that the number of apples in Carol's share is 18 more than the number of apples in Betty's share. Therefore, we can set up the equation:
Number of apples in Carol's share = Number of apples in Betty's share + 18
Using the ratios, we can express the number of apples in each person's share:
Number of apples in Betty's share = 3 * (Number of apples in Abbie's share)
Number of apples in Carol's share = x * (Number of apples in Abbie's share)
Substituting these values into the equation, we get:
x * (Number of apples in Abbie's share) = 3 * (Number of apples in Abbie's share) + 18
Simplifying the equation, we have:
x * (60 / (4 + x)) = 3 * (60 / (4 + x)) + 18
To solve for x, we can multiply both sides of the equation by (4 + x) to eliminate the denominators:
x * (4 + x) * (60 / (4 + x)) = 3 * (4 + x) * (60 / (4 + x)) + 18 * (4 + x)
Simplifying further:
60x = 3 * 60 + 18 * (4 + x)
60x = 180 + 72 + 18x
42x = 252
x = 6
Therefore, x = 6.
Learn more about ratios at: brainly.com/question/13419413
#SPJ11
Ms. Perreca examines several math errors of one of her students to try to figure out the pattern of errors. What is the pattern of error for these particular problems?
10+ 6 = 4
11 - 5 = 16
Answers
The pattern of error seems to be adding 4 and subtracting 10 in each calculation.
In the first example, the student adds 4 to the correct sum of 10 and 6, resulting in 14 instead of the correct answer of 16. In the second example, the student subtracts 10 from the correct difference of 11 - 5, resulting in 1 instead of the correct answer of 6.
From these examples, we can observe a consistent pattern in the errors made by the student. Specifically, the student is adding 4 to the correct sum and subtracting 10 from the correct difference. This suggests that the student may have misunderstood or misapplied the rules of addition and subtraction.
Learn more about pattern at https://brainly.com/question/275463
#SPJ11
Doug is a zookeeper in charge of monitoring the "aquatic" section at the North End Zoo. A baby dolphin was born on Wednesday and weighed 31 pounds. The dolphin is growing at an average rate of 2.3lbs per day. Write a function that can be used to find the weight, w(x), of the dolphin after x, days.
Answers
Answer:
w(x)=2.3x+31
Step-by-step explanation:
From the information given, the function would indicate that the weight of the dolphin after x days would be equal to the 31 pounds the baby weighed when it was born plus 2.3 lbs that is the average rate it is growing for the number of days:
w(x)= 2.3x+31, where:
w(x)= weight of the dolphin
x=number of days
Can you please help me I need to pass for my basketball game Tuesday please help if I don’t pass i can’t play !!

Answers
Answer:
x = 17
Step-by-step explanation:
The two given angles are supplementary angles, but also all angles on a straight light must add up to 180°:
3x + 14 + 7x - 4 = 180
Add like terms
3x + 7x + 14 - 4 = 180
10x + 10 = 180
Subtract 10 from both sides to isolate 10x:
10x + 10 - 10 = 180 - 10
10x = 170
Divide both sides by 10:
10x ÷ 10 = 170 ÷ 10
x = 17
Hope this helps!
25 POINTS!
Which of the following is an equation of a line PARALELL to the equation y=-4x+5
A. Y=4x+1
B. Y=-4x+1
C. Y=1/4x+1
D. Y=-1/4x+1
Which of the following is an equation of a line PERPENDICULAR to the equation y=-4x+5
A. Y=4x+1
B. Y=-4x+1
C. Y=1/4x+1
D. Y=-1/4x+1
Answers
A line perpendicular to y=-4x+5 must have a negative reciprocal slope to be perpendicular. Let’s find such a line:
m=-4, so a perpendicular line must have a slope of -(-1/4) = 1/4. Therefore, the best equation choice is C.)
In 15 words or fewer, will dividing the two polynomials in the table produce another polynomial? Why or why not?
Answers
Dividing two polynomials may produce another polynomial only when the divisor has a lower degree than the dividend. Otherwise, it will generally result in a rational function.
No, dividing two polynomials may not result in another polynomial. It can produce a rational function.
A polynomial is an algebraic expression consisting of terms with non-negative integer exponents. When two polynomials are divided, the result is not always a polynomial.
If the degree of the polynomial being divided (dividend) is higher than the degree of the polynomial dividing (divisor), then the result can be a polynomial with a lower degree. However, if the degree of the divisor is equal to or greater than the degree of the dividend, the result will generally be a rational function, which is a ratio of two polynomials.
A rational function has the form P(x)/Q(x), where P(x) and Q(x) are polynomials and Q(x) is not equal to zero. The division can introduce terms with negative or fractional exponents, making the result a rational function rather than a polynomial.
For more such questions on polynomial
https://brainly.com/question/1496352
#SPJ8
Solve 9x + 3 < 21 please help
Answers
Answer:
x<2
Step-by-step explanation:
Isolate the variable by dividing each side by factors that don't contain the variable.
Inequality Form:
x < 2 x < 2
Interval Notation:
( − ∞, 2)
Maurice can pack 100 cans in 20 minutes Is this a faster or slower rate than packing 160 cans in 40 minutes?
Answers
Answer:
Slower
Step-by-step explanation:
If 100 cans per 20 minutes continues, it would be 200 cans per 40 minutes, which is more than 160 cans per 40 minutes
You own a restaurant in a takeside town where 10,000 cars and 10,000 pedestrians pass by per day. 1.5% of cars with people each, and 3% of pedestrlans enter your restaurant, how many people enter per day?
Answers
Answer:
600
Step-by-step explanation
1.5% of /(10,000x2) is 300
3.0% of 10,000 is 300
Add them to get 600
Don't forget to thank me
A percentage is a way to describe a part of a whole. The number of people that enter the restaurant per day is 600 people.
What are Percentages?A percentage is a way to describe a part of a whole. such as the fraction ¼ can be described as 0.25 which is equal to 25%.
To convert a fraction to a percentage, convert the fraction to decimal form and then multiply by 100 with the '%' symbol.
Given that You own a restaurant in a lakeside town where 10,000 cars and 10,000 pedestrians pass by per day.
1.5% of cars with 2 people each, and 3% of pedestrians enter your restaurant.
The number of cars that has 2 people in each car passing the restaurant per day.
= 10,000 cars
The number of pedestrians that passes the restaurant each day.
= 10,000 people
The 1.5% of 10,000 cars will be,
= 1.5 / 100 x 10,000
= 150 cars
The number of people in 150 cars.
= 150 x 2
= 300 people _______(1)
The 3% of 10,000 pedestrians will be,
= 3 / 100 x 10,000
= 300 pedestrian
= 300 people ______(2)
The number of people that entered the restaurant.
= 1.5% of cars with 2 person on each car + 3% of pedestrians
From (1) and (2)
= 300 people + 300 people
= 600 people
Thus, the number of people that enter the restaurant per day is 600 people.
Learn more about Percentages here:
https://brainly.com/question/6972121
#SPJ2
find dy/dx
5. \( y=10 \bigcap_{4}^{x(x+1)(2 x-1)} \)
Answers
The derivative of the given expression `y=10 ∩_4^(x(x+1)(2x-1))` is `dy/dx = 4^(x(x+1)(2x-1)) * ln 4 * [(2x-1)(x+1) + 4x² - x]`.
Given, `y=10 ∩_4^(x(x+1)(2x-1))`
To find the derivative of the above expression, we can use the Chain rule of differentiation.
The Chain rule of differentiation is used to find the derivative of composite functions. This rule is also known as the function of a function rule.
The Chain Rule: If `f` and `g` are both differentiable functions, then the derivative of their composite is given by the product of the derivative of `g` with respect to `x` and the derivative of `f` with respect to `g`.
That is, if `y = f(g(x))`, then
`dy/dx = f'(g(x))g'(x)`
Hence, the derivative of the given expression `y=10 ∩_4^(x(x+1)(2x-1))` is given by:
dy/dx = d/dx [10 ∩_4^(x(x+1)(2x-1))]
dy/dx = 0 + d/dx [4^(x(x+1)(2x-1))] * d/dx [x(x+1)(2x-1)]
Now we need to find the derivative of the two terms separately.
(i) d/dx [4^(x(x+1)(2x-1))] = 4^(x(x+1)(2x-1)) * ln 4 * d/dx [x(x+1)(2x-1)]
(ii) d/dx [x(x+1)(2x-1)] = x'(x+1)(2x-1) + x(x+1)(2x-1)'= 1(x+1)(2x-1) + x(1)(4x-1)
So, dy/dx = 0 + 4^(x(x+1)(2x-1)) * ln 4 * [1(x+1)(2x-1) + x(1)(4x-1)]
Hence, dy/dx = 4^(x(x+1)(2x-1)) * ln 4 * [(2x-1)(x+1) + 4x² - x]
Learn more about Chain rule visit:
brainly.com/question/31585086
#SPJ11
what 25 time 358 divided by 1.6
Answers
Answer:
5593.75
Step-by-step explanation:
find the length of the graph of f(x)=ln(4sec(x)) for 0≤x≤π3.
Answers
To find the length of the graph of f(x)=ln(4sec(x)) for 0≤x≤π/3, we first need to compute the derivative of the function.
f(x) = ln(4sec(x))
f'(x) = (1/sec(x)) * (4sec(x)) * tan(x) = 4tan(x)
Next, we use the arc length formula:
L = ∫ [a,b] √[1 + (f'(x))^2] dx
Substituting in the values, we get:
L = ∫ [0,π/3] √[1 + (4tan(x))^2] dx
We can simplify this by using the identity 1 + tan^2(x) = sec^2(x):
L = ∫ [0,π/3] √[1 + (4tan(x))^2] dx
= ∫ [0,π/3] √[1 + 16tan^2(x)] dx
= ∫ [0,π/3] √[sec^2(x) + 16] dx
= ∫ [0,π/3] √[(1 + 15cos^2(x))] dx
= ∫ [0,π/3] √15cos^2(x) + 1 dx
Using the substitution u = cos(x), we get:
L = ∫ [0,1] √(15u^2 + 1) du
This can be solved using trigonometric substitution, but the details are beyond the scope of this answer. The final result is:
L = 4/3 * √(15) * sinh^(-1)(√15/4) - √15/2
Therefore, the length of the graph of f(x)=ln(4sec(x)) for 0≤x≤π/3 is approximately 3.195 units.
To know more about derivative visit:
https://brainly.com/question/29144258
#SPJ11
‼️(15 points)‼️
The aquarium below is 12 in. wide, 36 in. long, and 24 in. tall. It is filled with water, leaving 1 inch of the aquarium empty at the top.
How many cubic feet of water are in the aquarium?
A. 72 ft
OB. 61.5 ft
OC. 6 ft
OD. 5.75 ft?
Answers
Answer:
OC.6 ft hope this helps you
Answer: 6 ft
Step-by-step explanation:
L×w×h 36×12×24=10368in
1 cubic foot = 1728in 10368÷1728=6