Find the unit rate (How much for
one shirt?):
$98.73 for 6 shirts (round to the
nearest hundredth).
Answers
Answer:
$16.455
Step-by-step explanation:
98.73/6 = y
16.455 = y
Related Questions
The equation of the line is perpendicular to y= 1/2X +3 and passes through -2 and 5 in slope intercept form

Answers
The slope-intercept equation of a line has the form
\(y=m\cdot x+b,\)where m is the slope of the line and b is its y-intercept.
Now, there is a very interesting relationship between the slopes (m_1 and m_2) of perpendicular lines:
\(m_1=-\frac{1}{m_2}\text{.}\)Looking at the given equation, we can say that its slope is 1/2. Then,
\(m=-\frac{1}{\frac{1}{2}}=-2.\)Then, our desired equation becomes
\(y=-2x+b\text{.}\)Now, we know that our line passes through (-2,5). This means that
\(5=-2\cdot(-2)+b\text{.}\)Solving this equation for b, we get
\(\begin{gathered} 5=4+b, \\ 4+b=5, \\ b=5-4, \\ b=1. \end{gathered}\)AnswerThe desired line has equation
\(y=-2x+1.\)PLS HELP WILL GIVE BRAINLIST

Answers
Answer:
The answer is 1050
Step-by-step explanation:
HELP WILL MARK BRAINLIEST ANSWERRRRRR IF GOTTEN RIGHT

Answers
For the following exercises, consider the function f(x) = (1+x)^1/x. Round all answers to five decimal places. Evaluate f(-0.01).
Answers
The value of f(-0.01) is approximately 0.99005.
To evaluate f(-0.01), we substitute -0.01 into the function f(x) = (1+x)^(1/x). Thus, we have f(-0.01) = (1+(-0.01))^(1/(-0.01)).
Using a calculator, we simplify this expression to f(-0.01) = 0.99005. Therefore, the value of f(-0.01) rounded to five decimal places is approximately 0.99005.
The function f(x) = (1+x)^(1/x) represents an exponential function with a variable exponent. In this case, we are evaluating the function at x = -0.01.
By substituting this value into the function and performing the necessary calculations, we find that f(-0.01) is approximately 0.99005. This means that when x is equal to -0.01, the function value is approximately 0.99005.
For more such answers on function
https://brainly.com/question/11624077
#SPJ8
Nelson lands 4650 on 2% interest rate. He plans to pay this after 2 months. What will the total principal and interest payment be?
Answers
The total principal and interest payment that Nelson will have to pay after 2 months is $4665.50.
To calculate the total principal and interest payment, we need to determine the interest amount and add it to the principal.
First, let's find the interest amount:
Interest = Principal x Interest Rate x Time
Given:
Principal = $4650
Interest Rate = 2% per year
Time = 2 months
Since the interest rate is given on an annual basis, we need to convert the time from months to years. There are 12 months in a year, so 2 months is equivalent to 2/12 = 1/6 years.
Interest = $4650 x 0.02 x (1/6) = $15.50
Now, we can calculate the total principal and interest payment:
Total Payment = Principal + Interest
Total Payment = $4650 + $15.50 = $4665.50
For more such questions on principal visit:
https://brainly.com/question/25720319
#SPJ8
6 divided by 3/4 using tape diagrams
Answers
Answer:
Step 1: Read the entire problem. Students will find themselves reading the story numerous times. Each time will have a different purpose in the model drawing process. Step 2: Turn the question into a sentence with a space for the answer.
araceli renta un local rectangular de 4.2 metros de frente y 7.3 metros de largo para su panaderia, ¿cuantos metros cuadrados tiene el local que rento?
Answers
The number of square meters that the space that Araceli rents is, is 30. 66 square meters.
How to find the area ?The space that Araceli rents has a rectangular space so to find the area of the rectangular space that Araceli rents, we need to multiply the length by the width.
The given width is 4. 2 meters and the length is 7. 3 meters.
The area of the space in square meters is therefore :
Area = Length × Width
Area = 7. 3 meters × 4. 2 meters
Area = 30. 66 square meters
In conclusion, the space that Araceli rents has an area of 30. 66 square meters.
Find out more on area at https://brainly.com/question/2129070
#SPJ1
–5x+4
constant
coefficient:
variable:
Answers
Answer:
constant: 4
coefficient:-5
variable:x
Step-by-step explanation:
You can easily search up the definition of each word and figure it out just saying. It's fine if u wanna do this-
I need help! 25 brainly points!

Answers
The surface areas for each figures are:
220 ft² 410 cm²596 cm²360 cm²Surface area of cylinders include: 132π mm²22π ft²396π square inches.How to calculate surface areas?1. The surface area of the cuboid is:
Top and bottom: 2(10 ft x 4 ft) = 80 ft²
Front and back: 2(10 ft x 5 ft) = 100 ft²
Sides: 2(4 ft x 5 ft) = 40 ft²
Total surface area = 80 + 100 + 40 = 220 ft²
2. The surface area of the cuboid is:
Top and bottom: 2(18 cm x 5 cm) = 180 cm²
Front and back: 2(18 cm x 5 cm) = 180 cm²
Sides: 2(5 cm x 5 cm) = 50 cm²
Total surface area = 180 + 180 + 50 = 410 cm²
3. The surface area of the prism is:
Top and bottom: 2(5 cm x 14 cm) = 140 cm²
Front and back: 2(5 cm x 12 cm) = 120 cm²
Sides: 2(12 cm x 14 cm) = 336 cm²
Total surface area = 140 + 120 + 336 = 596 cm²
4. The surface area of the stacked cuboids is:
Top and bottom of first cuboid: 2(6 cm x 7 cm) = 84 cm²
Front and back of first cuboid: 2(6 cm x 2 cm) = 12 cm²
Sides of first cuboid: 2(7 cm x 2 cm) = 28 cm²
Front and back of second cuboid: 2(7 cm x 2 cm) = 28 cm²
Sides of second cuboid: 2(2 cm x 4 cm) = 8 cm²
Front and back of third cuboid: 2(2 cm x 10 cm) = 40 cm²
Sides of third cuboid: 2(10 cm x 8 cm) = 160 cm²
Total surface area = 84 + 12 + 28 + 28 + 8 + 40 + 160 = 360 cm²
5. The surface area of the cylinder is:
Top and bottom: 2π(6 mm)² = 72π mm²
Side: 2π(6 mm)(5 mm) = 60π mm²
Total surface area = 72π + 60π = 132π mm²
6. The surface area of the cylinder is:
Top and bottom: 2π(1 ft)² = 2π ft²
Side: 2π(1 ft)(10 ft) = 20π ft²
Total surface area = 2π + 20π = 22π ft²
7. The surface area of the cylinder stacked on a cube is:
Top and bottom of cylinder: 2π(5 m)² = 50π m²
Side of cylinder: 2π(5 m)(8 m) = 80π m²
Surface area of cube: 6(10 m x 13 m) = 780 m²
Total surface area = 50π + 80π + 780 = (130π + 780) m²
8. The surface area of the cylinder is:
Top and bottom: 2π(9 in)² = 162π in²
Side: 2π(9 in)(4 in) = 72π in²
Therefore, the total surface area of the cylinder is:
2(162π in²) + 72π in² = 396π in²
So the surface area of the cylinder is 396π square inches.
Find out more on surface area here: https://brainly.com/question/16519513
#SPJ1
Image transcribed:
Find the surface area of each figure.
10 ft
18 cm
5 cm
4 ft
5 ft
3.
4.
6 cm
7 cm
2 cm
5 cm
12 cm
14 cm
4 cm
10 cm
8 cm
Find the surface area of each cylinder. Leave your answer in terms of π.
5.
6 mm
6.
1 ft
5 mm
10 ft
7.
5 m
8.
4 in.
8 m
10 m
9 in.
13 m
11 m
247
Journal and Practice Workbook
Geometry
Please answer ASAP I will brainlist

Answers
Answer:
log(3x⁹y⁴) = log 3 + 9 log x + 4 log y
Answer:
\(\log 3+ 9\log x +4 \log y\)
Step-by-step explanation:
Given logarithmic expression:
\(\log 3x^9y^4\)
\(\textsf{Apply the log product law:} \quad \log_axy=\log_ax + \log_ay\)
\(\log 3+\log x^9 +\log y^4\)
\(\textsf{Apply the log power law:} \quad \log_ax^n=n\log_ax\)
\(\log 3+ 9\log x +4 \log y\)
Use the commutative and associative properties as needed to simplify the expression. (12+a)+14
Answers
Answer:
26+a
Step-by-step explanation:
(12+a)+14
(12+14)+a
26+a
please help
the height ( in cm) of 12 players of a team are as follows : 160,150,158,159,160,160,162,165,166,167,170,175 find the median height of the team.
Answers
Answer:
Step-by-step explanation:
160,150,158,159,160,160,162,165,166,167,170,175
Write the 12 numbers in ascending order:
150, 158, 159, 160, 160, 160, 162, 165, 166, 167, 170, 175
We need the middle number but there is no middle number:
150, 158, 159, 160, 160, 160, 162, 165, 166, 167, 170, 175
We have split the numbers into 2 even amounts and there is no number in the middle so we take the middle 2 number and find there average:
150, 158, 159, 160, 160, 160, 162, 165, 166, 167, 170, 175
Average of 160 and 162 \(=\frac{160+162}{2} =161\).
SOLUTION: Median is 161cm.
Given the function () = $
% ) − 3 + 5, determine the inverse relation. [4]
7) Determine the sum of the arithmetic series 5 + 18 + 31 + 44 + ... 161 [3]
8) If the 11th term of a geometric sequence is 32 times larger than the 6th term, then
what is the common ratio of the sequence?
![Given the function () = $% ) 3 + 5, determine the inverse relation. [4]7) Determine the sum of the arithmetic](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/yWsdb1JfpWQtxKxmLuxYT8leNd6DrBG5.png)
Answers
The inverse of the function f(x) = 1/3x^2 - 3x + 5 is f-1(x) = 9/2 + √[3(x + 7/4)], the sum of the arithmetic series is 1078 and the common ratio of the sequence is 2
The inverse of the function?The function is given as:
f(x) = 1/3x^2 - 3x + 5
Next, we rewrite the function as in vertex form
Using a graphing calculator, the vertex form of the function f(x) = 1/3x^2 - 3x + 5 is
f(x) = 1/3(x - 9/2)^2 - 7/4
Express f(x) as y
y = 1/3(x - 9/2)^2 - 7/4
Swap x and y
x = 1/3(y - 9/2)^2 - 7/4
Add 7/4 to both sides
1/3(y - 9/2)^2 = x + 7/4
Multiply through by 3
(y - 9/2)^2 = 3(x + 7/4)
Take the square root of both sides
y - 9/2 = √[3(x + 7/4)]
Add 9/2 to both sides
y = 9/2 + √[3(x + 7/4)]
Rewrite as an inverse function
f-1(x) = 9/2 + √[3(x + 7/4)]
Sum of arithmetic seriesHere, we have:
5 + 18 + 31 + 44 + ... 161
Calculate the number of terms using:
L = a + (n -1)d
So, we have:
161 = 5 + (n - 1) * 13
This gives
(n - 1) * 13 = 156
Divide by 13
n - 1 = 12
Add 1
n = 13
The sum is then calculated as:
Sn = n/2 * [a + L]
This gives
Sn =13/2 * (5 + 161)
Evaluate
Sn = 1078
Hence, the sum of the arithmetic series is 1078
The common ratio of the sequenceHere, we have:
T11 = 32 * T6
The nth term of a geometric sequence is
Tn = ar^(n-1)
This gives
ar^10 = 32 * ar^5
Divide by ar^5
r^5 = 32
Take the fifth root
r = 2
Hence, the common ratio of the sequence is 2
Read more about sequence at:
https://brainly.com/question/7882626
#SPJ1
misha and his sister are using 5 foot and 8 foot landscaping timbers to enclose a vegetable garden they bought 40 timbers the total cost for the timbers was $288 which pair of equations could be used to find the number of timbers of each size that they brought?
Answers
Answer:
x+y=40 and 6x+9y=288
Find how much money needs to be deposited now into an account to obtain $1,200 (Future Value) in 15 years if the interest rate is 7% per year compounded monthly (12 times per year).
Answers
\(~~~~~~ \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+\frac{r}{n}\right)^{nt} \quad \begin{cases} A=\textit{accumulated amount}\dotfill & \$ 1200\\ P=\textit{original amount deposited}\\ r=rate\to 7\%\to \frac{7}{100}\dotfill &0.07\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{monthly, thus twelve} \end{array}\dotfill &12\\ t=years\dotfill &15 \end{cases}\)
\(1200 = P\left(1+\frac{0.07}{12}\right)^{12\cdot 15} \implies 1200=P\left( \frac{1207}{1200} \right)^{180} \\\\\\ \cfrac{1200}{ ~~ \left( \frac{1207}{1200} \right)^{180} ~~ }=P\implies 421.21\approx P\)
Part variability is critical in the manufacturing of ball bearings. Large variances in the sizeof the ball bearings cause bearing failure and rapid wearout. Production standards call fora maximum variance of .0001 when the bearing sizes are measured in inches. Asample of15 bearings shows a sample standard deviation of .014 inches.
a. use a=.10 to determine weather the sample indicates that the maximum acceptable variance is being exceeded.
b. Compute the 90% confidence interval estimate of the variance of the ball bearing in the population
Back of the book answer:
a.)X^2=27.44 P-val between .01 and .025 Reject null hyp., variance exceeds maximum requirements
b.).00012 to .00042 Obviously I know the final answer, but what are the steps to get there
Answers
For part a, you can use a chi-squared test to determine whether the variance in the sample exceeds the maximum acceptable variance in the population.
The null hypothesis for this test is that the variance in the sample is equal to or less than the maximum acceptable variance, and the alternative hypothesis is that the variance in the sample is greater than the maximum acceptable variance.
To perform the test, you need to first calculate the chi-squared statistic, which is given by:
X² = (n-1) * s² / σ²
where n is the sample size (in this case, 15), s is the sample standard deviation (in this case, 0.014 inches), and σ is the maximum acceptable variance (in this case, 0.0001 inches).
Plugging in the values, you get:
X² = (15-1) * .014² / .0001² = 27.44
Next, you need to determine the degrees of freedom for the test. In this case, the degrees of freedom is equal to the sample size minus 1, so the degrees of freedom is 14.
With the chi-squared statistic and the degrees of freedom, you can look up the p-value in a chi-squared table or use a chi-squared calculator to determine the p-value. The p-value is the probability of observing a chi-squared statistic as large or larger than the one you calculated, assuming the null hypothesis is true.
If the p-value is less than the significance level (in this case, .10), then you can reject the null hypothesis and conclude that the variance in the sample exceeds the maximum acceptable variance. In this case, the p-value is between 0.01 and 0.025, so you can reject the null hypothesis and conclude that the variance in the sample exceeds the maximum acceptable variance.
For part b, you can use a t-test to construct a 90% confidence interval estimate of the variance in the population. The confidence interval is an interval estimate of the true variance in the population, and the 90% confidence level means that there is a 90% probability that the true variance in the population falls within the confidence interval.
To construct the confidence interval, you first need to calculate the standard error of the variance, which is given by:
SE = s / √(n-1)
where s is the sample standard deviation and n is the sample size. Plugging in the values, you get:
SE = 0.014 / √(15-1) = 0.0041
Next, you need to determine the t-value for the confidence interval. The t-value is based on the degrees of freedom and the confidence level. With 14 degrees of freedom and a 90% confidence level, the t-value is 1.76.
With the standard error and the t-value, you can construct the confidence interval as follows:
Lower bound = s² - t * SE = .014² - 1.76 * 0.0041 = 0.00012 inches
Upper bound = s² + t * SE = .014² + 1.76 * 0.0041 = 0.00042 inches
Therefore, the 90% confidence interval estimate of the variance of the ball bearings in the population is .00012 to .00042 inches.
Learn more about Standard deviation at:
brainly.com/question/475676
#SPJ4
The Lim household paid $45 for electricity usage in a certain month. Find in kWh, the amount of electricity they used in that month if each electricity (in kWh) is charged at $0.20
Answers
The Lim household used 225 kWh of electricity in that month. The solution has been obtained by using the arithmetic operations.
What are arithmetic operations?
All real numbers are thought to be adequately described by the four basic operations, often known as "arithmetic operations." The mathematical operations quotient, product, sum, and difference come after division, multiplication, addition, and subtraction.
We are given that the Lim household paid $45 for electricity usage in a certain month and each electricity (in kWh) is charged at $0.20.
Let the electricity used be x.
So, we get an equation as
⇒ 0.20x = $45
Using the division operation, we get
⇒ x = 225 kWh
Hence, the Lim household used 225 kWh of electricity in that month.
Learn more about arithmetic operations from the given link
brainly.com/question/30283549
#SPJ1
What is the sin B?
/21
B
5
2
sin (B) =
[?]
![What is the sin B?/21B52sin (B) =[?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/bJqEBQdNtkeNzRPqszdQkxPqXUYlMPak.png)
Answers
Answer:
Step-by-step explanation:
sin (B) = \(\frac{2}{5}\)
Please i need the answer fast k12
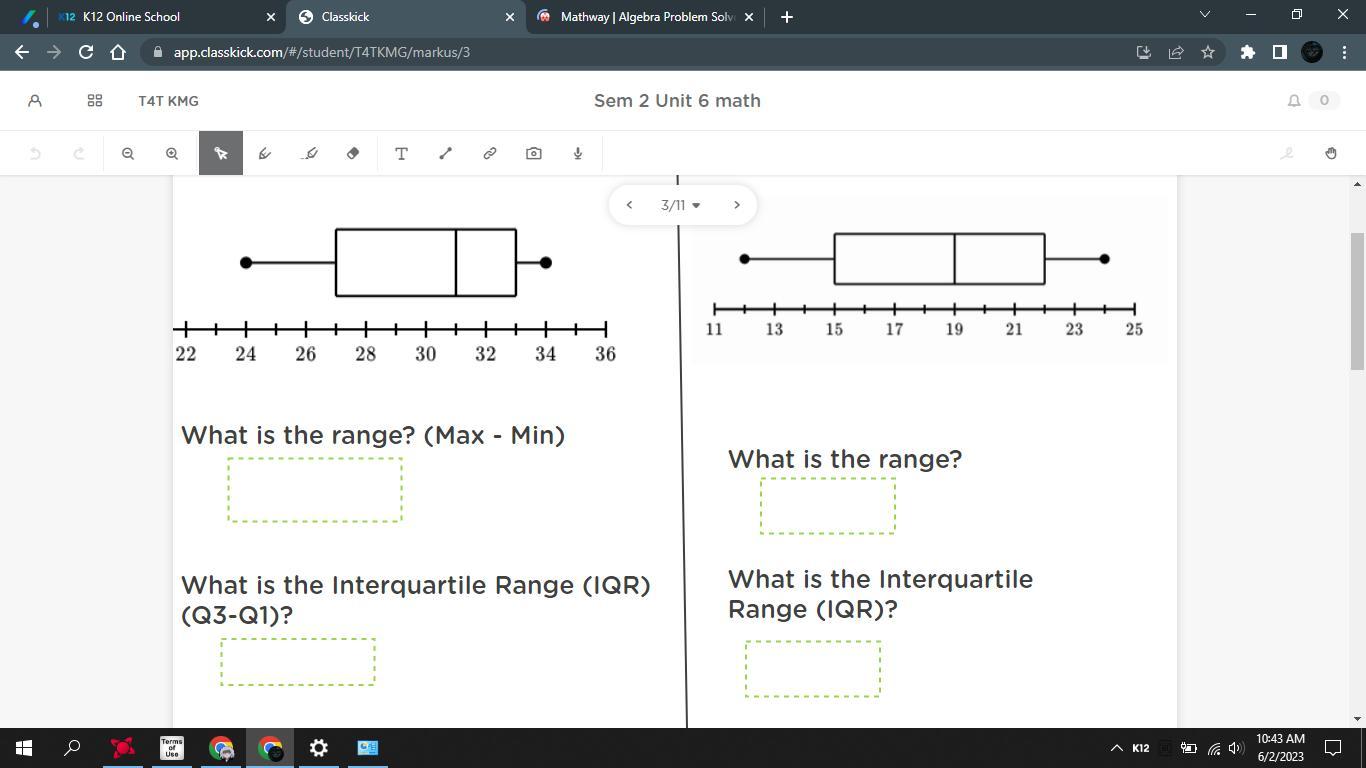
Answers
(A) The range and IQR for boxplot 1 is 10 and 6 respectively.
(B) The range and IQR for boxplot 2 is 12 and 7 respectively.
What is the IQR?The interquartile range defines the difference between the third and the first quartile.
The formula for the interquartile range is given below.
Interquartile range = Upper Quartile – Lower Quartile = Q3 – Q1
What is the range?The range is the difference between the lowest and highest values.
The formula for the interquartile range is given below.
Range = Maximum – Minimum
(A) For boxplot 1, we need to find the range and IQR from the given data set.
So, let 34 be the maximum and 24 be the minimum.
\(\text{Range}=\sf 34-24\)
\(\text{Range}=\sf10\)
Therefore, the range is 10.
Now time to find the IQR.
So, let 33 be Q3 and 27 be Q1.
\(\text{IQR}=\sf 33-27\)
\(\text{IQR}=\sf 6\)
Therefore, the IQR is 6.
(B) Now for boxplot 2, we will do the same thing as from part A.
Let's find the range.
So, let 24 be the maximum and 12 be the minimum.
\(\text{Range}=\sf 24-12\)
\(\text{Range}=\sf12\)
Hence, the range is 12.
Now for the IQR.
So, let 22 be Q3 and 15 be Q1.
\(\text{IQR}=\sf 22-15\)
\(\text{IQR}=\sf 7\)
Hence, the IQR is 7.
To know more about the range and IQR, visit:
https://brainly.com/question/31752116
#SPJ5
Please help a brotha out

Answers
Answer: a=1,b=1
Step-by-step explanation:
b
Lester Hollar is vice president for human resources for a large manufacturing company. In recent years, he has noticed an increase in absenteeism that he thinks is related to the general health of the employees. Four years ago, in an attempt to improve the situation, he began a fitness program in which employees exercise during their lunch hour. To evaluate the program, he selected a random sample of eight participants and found the number of days each was absent in the 6 months before the exercise program began and in the 6 months following the exercise program. Following are the results.
Employee Before After
1 8 7
2 7 3
3 8 2
4 8 4
5 6 5
6 7 10
7 6 4
8 8 9
At the 0.050 significance level, can he conclude that the number of absences has declined?
a. Compute the test statistic.
b. Compute the p-value.
Answers
The p-value can also be calculated using a t-distribution table or a statistical software package. Using a two-tailed test with 7 degrees of freedom and a significance level of 0.05, we obtain a p-value of 0.073.
How to solve the question?
To determine whether the fitness program has had a significant effect on reducing employee absenteeism, we need to conduct a hypothesis test.
Null hypothesis: The average number of absences before and after the fitness program are the same.
Alternative hypothesis: The average number of absences after the fitness program is less than before the program.
To test this hypothesis, we can use a one-tailed paired t-test with a significance level of 0.05. We will calculate the difference between the number of absences before and after the program for each employee, and then compute the mean and standard deviation of the differences. The t-test statistic will then be calculated as the mean difference divided by the standard deviation of the differences, multiplied by the square root of the sample size.
Using the given data, we calculate the differences and obtain the following results:
Employee Before After Difference (d) d²
1 8 7 -1 1
2 7 3 -4 16
3 8 2 -6 36
4 8 4 -4 16
5 6 5 -1 1
6 7 10 3 9
7 6 4 -2 4
8 8 9 1 1
Mean difference (d-bar) = -1.25
Standard deviation of differences (s) = 3.27
Sample size (n) = 8
The t-test statistic can now be calculated as:
t = (d-bar / (s / √(n))) = (-1.25 / (3.27 / √(8))) = -1.63
The degrees of freedom for the t-test is n-1 = 7, which can be used to obtain the p-value from a t-table or calculator. Using a one-tailed test with a significance level of 0.05 and 7 degrees of freedom, the critical t-value is -1.895.
Since our calculated t-value (-1.63) is greater than the critical t-value (-1.895), we fail to reject the null hypothesis. In other words, we do not have sufficient evidence to conclude that the fitness program has resulted in a significant reduction in employee absenteeism.
The p-value can also be calculated using a t-distribution table or a statistical software package. Using a two-tailed test with 7 degrees of freedom and a significance level of 0.05, we obtain a p-value of 0.073. Since this p-value is greater than the significance level, we again fail to reject the null hypothesis.
To know more about statistics visit :-
https://brainly.com/question/15525560
#SPJ1
. If α and β are the roots of
2x^2+7x-9=0 then find the equation whose roots are
α/β ,β/α
Answers
Answer:
\(18x^2+85x+18 = 0\)
Step-by-step explanation:
Given Equation is
=> \(2x^2+7x-9=0\)
Comparing it with \(ax^2+bx+c = 0\), we get
=> a = 2, b = 7 and c = -9
So,
Sum of roots = α+β = \(-\frac{b}{a}\)
α+β = -7/2
Product of roots = αβ = c/a
αβ = -9/2
Now, Finding the equation whose roots are:
α/β ,β/α
Sum of Roots = \(\frac{\alpha }{\beta } + \frac{\beta }{\alpha }\)
Sum of Roots = \(\frac{\alpha^2+\beta^2 }{\alpha \beta }\)
Sum of Roots = \(\frac{(\alpha+\beta )^2-2\alpha\beta }{\alpha\beta }\)
Sum of roots = \((\frac{-7}{2} )^2-2(\frac{-9}{2} ) / \frac{-9}{2}\)
Sum of roots = \(\frac{49}{4} + 9 /\frac{-9}{2}\)
Sum of Roots = \(\frac{49+36}{4} / \frac{-9}{2}\)
Sum of roots = \(\frac{85}{4} * \frac{2}{-9}\)
Sum of roots = S = \(-\frac{85}{18}\)
Product of Roots = \(\frac{\alpha }{\beta } \frac{\beta }{\alpha }\)
Product of Roots = P = 1
The Quadratic Equation is:
=> \(x^2-Sx+P = 0\)
=> \(x^2 - (-\frac{85}{18} )x+1 = 0\)
=> \(x^2 + \frac{85}{18}x + 1 = 0\)
=> \(18x^2+85x+18 = 0\)
This is the required quadratic equation.
Answer:
α/β= -2/9 β/α=-4.5
Step-by-step explanation:
So we have quadratic equation 2x^2+7x-9=0
Lets fin the roots using the equation's discriminant:
D=b^2-4*a*c
a=2 (coef at x^2) b=7(coef at x) c=-9
D= 49+4*2*9=121
sqrt(D)=11
So x1= (-b+sqrt(D))/(2*a)
x1=(-7+11)/4=1 so α=1
x2=(-7-11)/4=-4.5 so β=-4.5
=>α/β= -2/9 => β/α=-4.5
so I don't know what 5*7 is because it confusing
Answers
Answer:
35/16
Explanation:
(5*7)/2^4
= 35/2^4
= 35/16
Note:
Please mark as brainliest! <3
Help help help help help

Answers
Answer:
the answer would be 4m
hope this helped
Answer:
4m
Well there's 4 m's being added so to put it in simple terms, it would be 4m.
A bag contains colored tiles.
33 tiles are red
66 tiles are green
33 tiles are blue
A tile will be randomly selected from the bag. What is the on
probability in decimal form that the tile selected will be green?

Answers
Answer:
0.5
Step-by-step explanation:
Add everything together 33+66+33 = 132
Then 66/132, = 1/2 or 0.5
12Select the correct answer.What is the simplified form of this expression?(3 - 13x-7x7) – (5x2 + 12x - 10)OA 3x7 - 25x-2OB. -128 - x-7OC -12x - 25x-7OD-12x2 - 25x + 13MereNext
Answers
Find c and round to the nearest tenth

Answers
Answer:
\( c = 15.5 \)
Step-by-step explanation:
Using the Law of Cosines, c² = a² + b² - 2ab*cos(C), let's find c.
Where,
a = 15 ft
b = 20 ft
C = 50°
Thus:
\( c^2 = 15^2 + 20^2 - 2*15*20*cos(50) \)
\( c^2 = 625 - 600*0.6429 \)
\( c^2 = 625 - 600*0.6429 \)
\( c^2 = 625 - 385.74 \)
\( c^2 = 239.26 \)
\( c = \sqrt{239.26} \)
\( c = 15.5 \) (nearest tenth)
Answer:
c sorry gotta get points.
Step-by-step explanation:
Simplify and show your work. \((6i)(-2i)(-6-4i)\)
Answers
Answer:
- 72 - 48i
Step-by-step explanation:
note that i² = - 1
(6i)(- 2i)(- 6 - 4i)
= - 12i²(- 6 - 4i)
= - 12(- 1)(- 6 - 4i)
= 12(- 6 - 4i) ← distribute parenthesis by 12
= - 72 - 48i
If the line through the points (1,2) and (1,a) is parallel to 6x+2y=-2, what is the value of a?
Answers
Two lines are parallel if their slopes are equal. To find the slope of the line through the points (1,2) and (1,a), we can use the formula:
(y2 - y1) / (x2 - x1) = (a - 2) / (1 - 1) = a - 2
To find the slope of the line 6x + 2y = -2, we can rewrite it in slope-intercept form (y = mx + b) by isolating y:
2y = -6x - 2
y = -3x - 1
So the slope of this line is -3.
Since the line through the points (1,2) and (1,a) is parallel to 6x + 2y = -2, we know that the slopes must be equal. Therefore:
a - 2 = -3
Solving for a:
a = -1
So the value of a is -1.
Pls hurry I’m being timed the first to comment gets brainleist answer
Answers
Answer:
|3| < |-7| and 3>-7
Step-by-step explanation:
The absolute value of -7 = 7, and 3 < 7.