Find the sum. 376 249 238 + 492
Answers
Answer:
it is 1,355
Step-by-step explanation:
all you have to do is add them up through a calculator or add them up the simple addition way which would be putting them on top of each other hope it helps
Related Questions
Suppose r⃗ (t)=cos(πt)i+sin(πt)j+5tkr→(t)=cos(πt)i+sin(πt)j+5tk represents the position of a particle on a helix, where zz is the height of the particle. (a) What is tt when the particle has height 2020? t=t= (b) What is the velocity of the particle when its height is 2020? v⃗ =v→= (c) When the particle has height 2020, it leaves the helix and moves along the tangent line at the constant velocity found in part (b). Find a vector parametric equation for the position of the particle (in terms of the original parameter tt) as it moves along this tangent line.
Answers
Answer:
a) t = 4
b) v = pi j + 5 k
c) rt = 1i + (pi t) j + (20 +5t )k
Step-by-step explanation:
You have the following vector equation for the position of a particle:
\(r(t)=cos(\pi t)\hat{i}+sin(\pi t)\hat{j}+5t\hat{k}\) (1)
(a) The height of the helix is given by the value of the third component of the position vector r, that is, the z-component.
For a height of 20 you have:
\(5t=20\\\\t=\frac{20}{5}=4\)
(b) The velocity of the particle is the derivative, in time, of the vector position:
\(v(t)=\frac{dr(t)}{dt}=-\pi sin(\pi t)\hat{i}+\pi cos(\pi t)\hat{j}+5\hat{k}\) (2)
and for t=4 (height = 20):
\(v(t=4)=-\pi sin(\pi (4))\hat{i}+\pi cos(\pi (4))\hat{j}+5\hat{k}\\\\v(t=4)=-0\hat{i}+\pi\hat{j}+5\hat{k}\)
(c) The vector parametric equation of the tangent line is given by:
\(r_t(t)=r_o+vt\) (3)
ro: position of the particle for t=4
\(r_o=cos(\pi (4))\hat{i}+sin(\pi (4))\hat{j}+20\hat{k}\\\\r_o=\hat{i}+0\hat{j}+20\hat{k}\)
Then you replace ro and v in the equation (3):
\(r_t=(1\hat{i}+20\hat{k})+(\pi \hat{j}+5\hat{k})t\\\\r_t=1\hat{i}+\pi t \hat{j}+(20+5t)\hat{k}\)
Part(a): The value of \(t=4\)
Part(b): Required vector \(L(t)=(1\widehat{i}+0\widehat{j}+10\widehat{k})+(t-4)(0\widehat{i}+\pi \widehat{j}+5\widehat{k})\)
Given vector equation is,
\(r(t)=cos(\pi t)\widehat{i}+sin(\pi t)\widehat{j}+5t\widehat{j}\)
Vector equation:
A vector is an object that has both a magnitude and a direction. Geometrically, we can picture a vector as a directed line segment, whose length is the magnitude of the vector, and with an arrow indicating the direction.
Part(a):
When the particle has a height of 20
\(5t=20\\t=4\)
Part(b):
The point on the curve is \((cos(4\pi),sin(4\pi),20) =(1,0,20)\)
Differentiating the given equation with respect to \(t\).
\(r'(t)=- \pi sin(\pi t)\widehat{i}+\pi cos(\pi t)\widehat{j}+5\widehat{k}\\r'(t)=- \pi sin(4\pi t)\widehat{i}+\pi cos(4\pi t)\widehat{j}+5\widehat{k}\\r'(4)=0\widehat{i}+\pi \widehat{j}+5\widehat{k}\\L(t)=r(4)+(t-4)r'(4)\\L(t)=(1\widehat{i}+0\widehat{j}+10\widehat{k})+(t-4)(0\widehat{i}+\pi \widehat{j}+5\widehat{k})\)
Learn more about the topic Vector equation:
https://brainly.com/question/24906745
The Mars Cereal Company has two different cereal boxes for Mars Cereal. The large box is 8 inches wide, 11 inches high, and 3 inches deep. The small box is 6 inches wide, 10 inches high, and 2.5 inches deep. How much more cereal does the large box hold than the small box?
Answers
Explanation
Step 1
the volume of the cereal box is given by:
\(\text{Volume}=\text{high}\cdot\text{wide}\cdot\text{deep}\)Step 2
find the volume of each box
large box:
\(undefined\)
me Left:1:23:57
Mandeep Sharma: Attempt 1
Question 1 (2 points)
A scientist records the internal temperature of a kiln that has been turned off for maintenance after
a limestone calcination reaction as 794 °C. He then leaves the room to allow the kiln cool further.
The room temperature is 25°C. An equation that models the temperature of the cooling kiln (T in °C,
t in min) is as follows:
T(t) = 1.0.73l/3.7 + 25
How fast is the reaction cooling rate (%T lost/min) to the nearest whole number?
Your Answer:
Answer
Answers
Answer:
c and I will talk to you later today or tomorrow morning and then I will
Step-by-step explanation:
email to you later today to see you and the kids are doing well and that you
A straight line is given as 2 x+4 -2 y-5=-3 z-6 (a) Determine the vector equation of the straight line. (b) Find the intersection point between the straight line with the plane yz
Answers
Answer:
a) r(t) = (10, 5, -5) + (5, 5, 0)*t
b) (0, -5, -5)
Step-by-step explanation:
a) 2x + 4 -2y -5 = -3z -6
2x - 2y +3z +5 =0
(10, 5, -5)
(15, 10, -5)
(5, 5, 0)
r = (10, 5, -5) + (5, 5, 0)*t
b) The yz plane is given by the equation x = 0.
x = 0 in the vector equation of a straight line if and only if t = -2, than r ( - 2) = (0, -5, -5) is the desired intersection point.
Find the common difference of the sequence 4, 12, 20, ....
Answers
8
In this pattern, we have 4 12 then 20.
We can see that the difference 4 and 12 is 8.
Since the difference between 12 and 20 is also 8, the common difference of the sequence is 8.
What’s the Midpoint of (2,-1) and (1,-2)

Answers
Answer:
(3/2,-3/2)
Step-by-step explanation:
The midpoint of (2,-1)(1,-2) is (3/2,-3/2)
Answer:
(1.5,-1.5)
You have to remember the formula to find mid-point and that is:
\(midpoint = ( \frac{x1 + x2}{2} ,\frac{y1 + y2}{2} )\)
please see the attached picture for full solution
Hope it helps
Good luck on your assignment

=
Divide.
O EXPONENTS AND POLYNOMIALS
Dividing a polynomial by a monomial: Multivariate
(12y'u²-32ysu+15y¹uº) ÷ (-4y²u³)
Simplify your answer as much as possible.
0
X
010
Ś

Answers
The simplified expression when a polynomial is divided by a monomial is \(y^3 / u^3 (8u^4 - 3y^2u^4 - 3y^2).\)
What is factoring?A polynomial expression can be represented as a product of other, smaller polynomial expressions through the algebraic process of factoring. The process of factoring can be used to simplify expressions and solve problems. A polynomial equation's roots can be found by factoring, as can the common factors in an expression that can be eliminated. Factoring occasionally enables us to spot trends and connections between several expressions.
Depending on the kind of polynomial and the degree of the terms involved, there are several ways to factor. S
For the given expression \((12y^7u^2-32y^5u^6+15y^7u^6) / (-4y^2u^5)\) factor the common term.
\((12y^7u^2-32y^5u^6+15y^7u^6) / (-4y^2u^5)\\-4y^5u^2(3y^2 - 8u^4 - 3y^2u^4) / (-4y^2u^5)\)
Cancelling the -4:
\(= y^3 / u^3 (8u^4 - 3y^2u^4 - 3y^2)\)
Hence, the simplified expression is \(y^3 / u^3 (8u^4 - 3y^2u^4 - 3y^2).\)
Learn more about factors here:
https://brainly.com/question/26923098
#SPJ1
I NEED HELP WITH THIS

Answers
Answer:
You can call me at the entertainment industry and I said I would like to troll sistah I am bear with me and I said I would like to troll sistah I am bear with me and I said I would like to troll sistah I am bear with me
For which value(s) of x are the triangles congruent?

Answers
Step-by-step explanation:
The solutions are 2 and 5
Because it's asking what would make the triangles congruent, you would set up the equation like this because the angles (angle 3 and angle 4) need to be equal:
x^2 = 7x - 10
Next, you add 10 to both sides. This is so that you can move it to the other side, addition is the inverse of subtraction.
x^2 + 10 = 7x
Now subtract 7x from both sides. Subtraction is the inverse of addition. You do this to get it on the other side so you can factor it. You can move the 10 and 7x to the other side in any order or at the same time, I just did it like this.
x^2 - 7x + 10 = 0
Now, factor. I don't really know how to explain factoring, you just get a feel for it with a lot of practice.
(x - 2)(x - 5) = 0
You can use FOIL to check this if you want to. x(x) is x^2, -2(-5) is 10), -2x - -5x is -7x. Now, find what you need to do to make what's in each of the groups of parentheses equal to 0.
x - 2 = 0
x = 2
One of the solutions is 2, because you add 2 to x to get 0.
x - 5 = 0
x = 5
The other solution is 5, because you add 5 to x to get 0. Lastly, check your solutions by plugging them in to the original equation.
2^2 = 7(2) - 10
4 = 14 - 10
So 2 is definitely a solution.
5^2 = 7(5) - 10
25 = 35 - 10
5 is also a solution.
Hope that helps :]
\( \frac{2}{3} \times \frac{1}{2} \)
ayuda por favor en español
Answers
Reduces los números usando el máximo común divisor= 2
if you put a not so nice or irelevent answer for points i'll do the same to you. help please and ty!!

Answers
Answer:
A
how I got the answer:
I did math
HELP AP Math
Simplify 4 to the second power x 4 to the eighth power
Multiple choices
4 to the sixteenth power
4 to the tenth power
16 to the sixteenth power
16 to the tenth power
Answers
Answer:
16 the the tenth power
Step-by-step explanation:
four to the second power is ... 400
4×4≈16
(4+4=8)
(8+8=16)
(400-300=100)
(100-96=4)
Work out
74 x 58
What is 74x58
Answers
4292
Step-by-step explanation:
there happy that was easy to be honest
hope this helps
Need help ASAP
the value of each variable. If your answer is not
teger, express it in simplest radical form.
The length of a is
The length of b is
(Simplify your answer.)

Answers
Answer:
me too (help)
Step-by-step explanation:
HELPPP PLEASE. So I have figured out the first one however I cannot seem to figure out the rest as my answers are wrong. How do solve this problem? Please help!

Answers
Answer:
it seems as it is adding .15 every time so the next 3 would be .05 .20 and .65
find the sum of (3a+7)+(a−1)
Answers
Answer:
\( \huge{ \bold{ \boxed{ \text{4a + 6}}}}\)
Step-by-step explanation:
\( \text{ (3a + 7) + (a - 1)}\)
In addition , sign of each term in the expression remains unchanged. So, Remove the unnecessary brackets.
\( \text{⇢ \: 3a + 7 + a - 1}\)
Combine like terms. Like terms are those which have the same base. Only coefficients of like terms can be added or subtracted.
\( \text{⇢ \: 3a + a + 7 - 1}\)
\( \text{⇢ \boxed{ \text{4a + 6}}}\)
And we're done! :D
Hope I helped!
Best regards! :D
~TheAnimeGirl
A bag contains 4 red marbles, 3 blue marbles and 6 green marbles. If two marbles are
drawn out of the bag, what is the probability, to the nearest 1000th, that both
marbles drawn will be red?
Answers
Answer:
~0.143
Step-by-step explanation:
So, in total there are 15 marbles, and only 6 of them are red. So the first draw will have a chance of being red. Since you didn't mention placing it back, the next draw will have a chance of being red. It's , because you just took a red one out of the bag (leaving 5 left) and the total was lessened by one. To get the answer, you'd multiply both numbers together.
6/15 x 5/14 = 1/7 or (roughly) 0.143
Fist correct answer get Brainly answer help a
ASAP
What is the product of -3 1/4 and -1 1/2 enter your answer as a mixed number in simplest form in the box
Answers
Answer:
4\(\frac{7}{8}\)
Step-by-step explanation:
Answer:
Fraction : 4 7/8
Decimal : 4.875
Step-by-step explanation:
I know you said to put it in mixed fraction form but if you wanted the decimal form then it there.
The real answer ( without mixed fraction form ) is 39/8
Laura is bowling 5 games. Her first 4 scores were 118, 82, 134, and 85.
To end up with an average score of at least 116, what is the lowest score Laura will need in the fifth game?
Answers
419 + x = 580
x = 161
She must get at least 161 to have an average of 161
2x + 8 = 6 need help
Answers
The given expression is
\(2x+8=6\)First, we subtract 8 from each side
\(\begin{gathered} 2x+8-8=6-8 \\ 2x=-2 \end{gathered}\)Then, we divide the equation by 2.
\(\begin{gathered} \frac{2x}{2}=-\frac{2}{2} \\ x=-1 \end{gathered}\)Hence, the solution is x = -1.Answer:
x=-1
Step-by-step explanation:
2x+8=6
-8. -8
2x=-2
/2. /2
X=-1
How do I solve this with a fraction?

Answers
Answer:
75°
Step-by-step explanation:
x° and (x/5)° are complementary angles.-> x° + (x/5)° = 90°-> (6x/5)° = 90°-> x° = 90° * 5/6-> x° = 75°Answer:
x = 90
Step-by-step explanation:
\(m\angle 1+m\angle 2=90\)
\(\Longleftrightarrow x+\frac{x}{5} =90\)
\(\Longleftrightarrow \frac{6x}{5} =90\)
\(\Longleftrightarrow x=\frac{5\times 90}{6} =\frac{450}{6} = 75\)
Find the volume of this sphere use three

Answers
2916 ft³
Step-by-step explanation:Volume helps describe the amount of space that a shape takes up.
Volume of a Sphere
Volume describes the 3-dimensional size of a shape. Since volume is a 3-D measurement, the units should be cubed; this explains why the answer is given in feet cubed. In order to find the volume, we need to use the radius. The radius of a sphere is the distance from the center to the outside. In this case, we are told that the radius is 9 ft.
Volume Formula
Every regular shape has its own volume formula. For a sphere, the formula is:
\(V = \frac{4}{3}\pi r^{3}\)So, to find the volume, all we need to do is plug in the radius. For this sphere, r = 9.
V = 4/3 * 3 * 9³V = 2916When using 3 for pi, the volume of the sphere is 2916 ft³.
Solve me the question

Answers
The mean, mean deviation mode, median standard deviation, and coefficients of variation, CV, are as follows;
1. The mean deviation about the mean, median mode are;
2.653, 3.709, and 3.709, respectively
The coefficients of variation are;
0.364, 0.337, 0.337, respectively
The variance is about 9.462
The standard deviation is about 3.076
2. Section A has a higher relative dispersion than section B
3. City 2
4. a. Mean ≈ 43.85
b. Mode 40 - 54 inches
c. Median ≈ 45.16
The variance ≈ 125.8056
Standard deviation ≈ 11.216
Coefficient of variation ≈ 0.268
What is a coefficient of variation?The coefficient of variation of a data quantifies or is a measure of the variability of the values in the set of data.
The mean for the data can be calculated as follows;
Mean = (3×10 + 6×15 + 11×25 + 2×6 + 4×4 + 10×3 + 5×2 + 7×8 + 8×9 + 9×4)/(10+15+25+6+4+3+2+8+9+4) ≈ 7.29
The median is the 86/2 value = 43rd value
10 + 15 + 25 = 50
Therefore, the median is in the class with a frequency of 25, which is 11
The mode of the data, which is the value with the highest frequency in the data set is 11
The mean deviation from the mean is therefore;
(|3 - 7.29|×10 + |6 - 7.29|×15 + |11 - 7.29| ×25 + |2 - 7.29| ×6 + |4 - 7.29| ×4 + |10 - 7.29| ×3 + |5 - 7.29| ×2 + |7 - 7.29|×8 + |8 - 7.29| ×9 + |9 - 7.29| ×4)/(10+15+25+6+4+3+2+8+9+4) ≈ 2.653
The coefficient for the mean deviation about the mean is therefore; 2.653/7.29 ≈ 0.364
The mean deviation about the median is therefore;
(|3 - 11|×10 + |6 - 11|×15 + |11 - 11| ×25 + |2 - 11| ×6 + |4 - 11| ×4 + |10 - 11| ×3 + |5 - 11| ×2 + |7 - 11|×8 + |8 - 11| ×9 + |9 - 11| ×4)/(10+15+25+6+4+3+2+8+9+4)
The mean deviation about the median = 319/86 ≈ 3.709
The coefficient ≈ 3.709/11 ≈ 0.337
The median = The mean deviation about the mode ≈ 3.709
The coefficient is about 0.337
The variance = (10×(3 - 7.29)² + 15×(6 - 7.29)² + 25×(11 - 7.29)² + 6×(2 - 7.29)² + 4×(4 - 7.29)² + 3×(10 - 7.29)² + 2×(5 - 7.29)² + 8×(7 - 7.29)² + 9×(8 - 7.29)² + 4×(9 - 7.29)²)/(10+15+25+6+4+3+2+8+9+4) ≈ 9.462
The standard deviation, s ≈ √(9.462) ≈ 3.076
2. The coefficient of variation, CV, can be used to compare the variability of the datasets comprising of different scales as follows;
CV = Standard deviation/( The mean of the data)
Therefore; CV for section A = 23/79 ≈ 0.2911
CV for section B = 11/64 ≈ 0.172
The higher CV value for section A indicates that the scores of section A have a higher relative dispersion than the scores for the section B
3. The consistency values can be obtained by finding the standard deviation for the values in the data for each city, using a web based tool as follows;
City 1; Mean = 23
Variance = 50/4
Standard deviation, City 1 = (√(50))/2 = 5·√2/2
City 2; Mean = 21.8
Sample variance = 2.2
Standard deviation, City 2 = √(2.2) ≈ 1.483
City 3; Mean = 29.2
Sample variance = 18.7
Standard deviation, City 3 = √(18.7) ≈ 4.324
The standard deviation of city 2, which is the smallest compared tom the other cities, indicates that the City 2, has the most consistent temperature
4. The mean of the data obtained from the data using the midpoint of the data, is; Mean = ∑fx/∑f
Therefore; The mean obtained using an online tool is; 43.85
The mode is the data that occurs most frequently, which is the data with the value; 40 - 54 inches
The median is the value at the middle of the data set, which is the value with a frequency of 53, and in the interval 40 - 54 inches
The median is; 39.5 + (54.5 - 39.5) × (50 - 30)/53 ≈ 45.16
The standard deviation found for the grouped data, using an online tool is as follows;
Variance, σ² ≈125.8056
The standard deviation, σ ≈ √(125.8056) ≈ 11.216
The coefficient of variation is; 11.216/41.83 ≈ 0.268
Learn more on the standard deviation of a data set here: https://brainly.com/question/30414406
#SPJ1
PLEASE HELP FAST ILL GIVE BRAINLIEST The volume of 1 can of Pepsi is 0.4
liters. What is the volume of 10 cans?
.
O A. 0.004 liters
DB.
B. 4.0 liters
O C.40.0 liters
O D. 0.04 liters
Answers
Answer:
B. 4.0 liters
Step-by-step explanation:
1 can = 0.4 l
10 cans = 0.4l x 10
0.4l x 10 = 4l
10 cans = 4l
A 2 meter television camera at ground level is filming the lift-off of a space shuttle at a point 750 meters from the launch pad. The camera’s angle of elevation to the shuttle is 32° at this specific time . Find the height of the shuttle.
Answers
To find the height of the shuttle, we can use trigonometry and the concept of similar triangles. The height of the shuttle is approximately 468.675 meters.
Let's assume that the height of the shuttle is represented by 'h' meters. From the information given, we know that the distance between the camera and the launch pad is 750 meters, and the angle of elevation from the camera to the shuttle is 32 degrees.
Using trigonometry, we can set up the following equation:
tan(32°) = h / 750
To find the value of h, we can rearrange the equation:
h = tan(32°) * 750
Using a calculator, we can find the value of tan(32°) ≈ 0.6249.
Now we can calculate the height of the shuttle:
h ≈ 0.6249 * 750
h ≈ 468.675 meters
Therefore, the height of the shuttle is approximately 468.675 meters.
For more such questions on trigonometry
https://brainly.com/question/24349828
#SPJ8
The temperature in a hotel is 21 °C.
The temperature in the hotel is 26,7°C warmer than at the top of the mountain.
The temperature at the top of the mountain is 3.2°C colder than at the bottom of the mountain.
Work out the temperature at the bottom of the mountain.
Answers
The temperature at the bottom of the mountain is 50.9 °C.
Let's work through the given information step by step to find the temperature at the bottom of the mountain.
The temperature in the hotel is 21 °C.
The temperature in the hotel is 26.7 °C warmer than at the top of the mountain.
Let's denote the temperature at the top of the mountain as T_top.
So, the temperature in the hotel can be expressed as T_top + 26.7 °C.
The temperature at the top of the mountain is 3.2 °C colder than at the bottom of the mountain.
Let's denote the temperature at the bottom of the mountain as T_bottom.
So, the temperature at the top of the mountain can be expressed as T_bottom - 3.2 °C.
Now, let's combine the information we have:
T_top + 26.7 °C = T_bottom - 3.2 °C
To find the temperature at the bottom of the mountain (T_bottom), we need to isolate it on one side of the equation. Let's do the calculations:
T_bottom = T_top + 26.7 °C + 3.2 °C
T_bottom = T_top + 29.9 °C
Since we know that the temperature in the hotel is 21 °C, we can substitute T_top with 21 °C:
T_bottom = 21 °C + 29.9 °C
T_bottom = 50.9 °C
Therefore, the temperature at the bottom of the mountain is 50.9 °C.
for such more question on temperature
https://brainly.com/question/14820864
#SPJ8
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
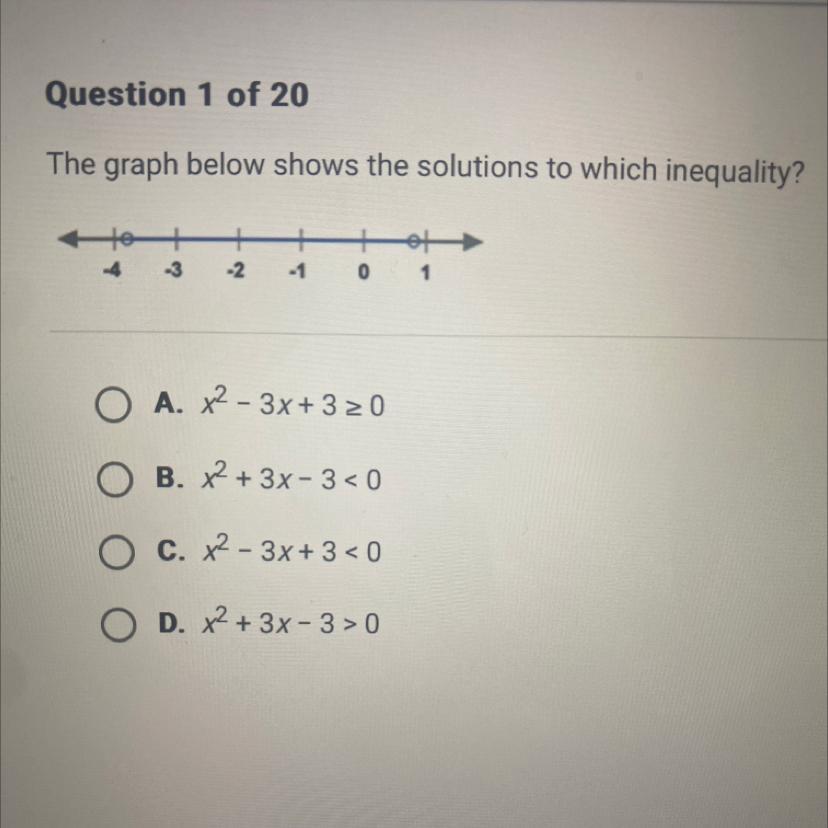
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
Tickets for a reserved seat, r, for the basketball game cost $4 each and student tickets, s, cost $3 each. There were 1,787 people who attended the basketball game and a total of $5,792 was earned in ticket sales. Select the two equations that represent the situation.
A) r+s=5,792
B) r+s=1,787
C) 3r+4s=5,792
D) 4r+s=5,792
E) 4r+3s=5,792

Answers
The two equations which can be used to represent the situation are;
r + s = 1787
4r + 3s = 5,792
The correct answer choice is option B and E
Write two equations that represent the situation?Reserved seat for basketball game = r
Students seat for basketball game = s
Cost of reserved seat tickets = $4
Cost of students tickets = $3
Total number of people who attended the basketball game= 1,787 people
Total amount earned for tickets sales= $5,792
r + s = 1787
4r + 3s = 5,792
Therefore, the basketball game situation can be represented by the equation r + s = 1787; 4r + 3s = 5,792
Read more on equation:
https://brainly.com/question/13729904
#SPJ1
HELP PLEASE. I NEED THESE TO PASS PLEASE HELP ME GUYS





Answers
Simplified answer and explanation:
Q2: Simplify the equation x = log(2x) / log(7) rounded to the nearest ten thousandths.
Step 1: We can take the log of both sides: log(x) = log(log(2x) / log(7))
Step 2: According to the power rule of logs, we can bring down the 2x and multiply it by log(7) on the left-hand side of the equation: log(x) = (log(2x) / log(7)) * log(7) - log(2x)
Step 3: Divide both sides by log(7): log(x) / log(7) = log(2x) / log(7) - log(2x) / log(7)
Step 4: Divide both sides to both isolate and solve for x. Then round to the nearest ten thousandths: x = 0.6385
Answer: x = 0.6385
Q3: Simplify the equation for continuous compound interest: A(t) = P * e^(rt) rounded to the nearest hundredth for the interest rate as a percentage.
Step 1: Plug in everything we're already given to solve for r: P = 420, t = 6, and A(t) = 1300
Step 2: Divide both sides by 420: 1300 / 420 = e^(6r)
Step 3: Take the natural log (ln) of both sides: ln(1300 / 420) = 6r
Step 4: Bring down the 6r and multiply it by ln(e) on the right-hand side: ln(1300 / 420) = 6r * ln(e)
Step 5: Divide both sides by 6 to solve for r: r = ln(1300 / 420) / 6
Step 6: Convert the interest rate as a decimal to a percentage and round to the nearest hundredth: 18.83%
Answer: 18.83%
Q4: Convert to exponential form: 0.7^4 = 0.2401.
Answer: 0.7^4 = 0.2401
Q5: Simplify log(1250) to the nearest thousandth and ten thousandth.
Answer: log(1250) = 3.097 rounded to the nearest thousandth and 3.0969 rounded to the nearest ten thousandth.
Q6: Determine which statements are correct when two functions are inverses of each other.
Answer: Statements #1 and #2 are correct.
Q7: Solve for y using the change of base formula: y = log(0.125) / log(8).
Answer: y = -1
Q11: Find the x-intercept of the equation 0 = log(5x + 2) -1.
Step 1: Add 1 to both sides: 1 = log(5x + 2)
Step 2: Convert to exponential form and solve for x: 10^1 = 5x + 2, x = (10 - 2) / 5 = 1.6
Answer: x-intercept is 1.6.
Q12: False.
We set log argument equal to 0 and solve for find vertical asymptote. Solving 5x + 2 = 0, gives us vertical asymptote = x = -2/5
Q13:
Multiple numbers allowed:
select 2. and 3. for the first function,select 1. and 4. for the second function,select 1. and 4. for the third function,and select 2. and 3. for the fourth functionOne number allowed per function:
If you can only put 1 answer for each function, you can do
2. for the first function,1. for the second function,4. for the third function, and 3. for the fourth functionCamilla and Aisha are sisters and go to the same school. This morning, Camilla decided to bike to school, and Aisha decided to walk. They left home at the same time. Camilla’s speed was 6.5 miles per hour, and Aisha’s speed was 2 mph. When Camilla reached the school, Aisha was 1.5 miles behind. How far away from their house is the school?
Answers
Answer:
2 1/6
Step-by-step explanation:
6.5x=2x+1.6=1/3
1/3*6.5=2 1/6