Find the specified area. The area under the graph of f over the interval (-1,3) f(x) = 5, if x < 1 and 5x^2 if x>=1 A 140 B 20 C 54 D 160 3
Answers
To find the total area under the graph of f over the interval (-1,3),
we add the two areas: 10 + 130/3 = 160/3.
Therefore, the answer is D) 160.
To find the area under the graph of f over the interval (-1,3)
for the function f(x) = {5, if x < 1 and 5x^2 if x>=1},
we need to calculate the area of the two parts separately since the function is piecewise.
Let's first find the area under the graph of f over the interval (-1,1):
For x < 1, the function f(x) = 5, which is a horizontal line.
Therefore, the area under the graph of f(x) over the interval (-1,1) is simply the area of the rectangle with height 5 and width 2 (since the interval is from -1 to 1).
This gives us an area of 5 * 2 = 10.
Now, let's find the area under the graph of f over the interval (1,3):
For x >= 1, the function f(x) = 5x^2, which is a parabola.
Therefore, we need to find the area under this curve over the interval (1,3).
The antiderivative of 5x^2 is (5/3)x^3, so we can use the definite integral to find the area:
∫[1,3] 5x^2 dx
= [(5/3)x^3]1,3
= (5/3)(3^3 - 1^3)
= (5/3)(26)
= 130/3
So the area under the graph of f over the interval (1,3) is 130/3.
To find the total area under the graph of f over the interval (-1,3),
we add the two areas:
10 + 130/3 = 160/3.
Therefore, the answer is D) 160.
To know more about function visit:
https://brainly.com/question/30721594
#SPJ11
Related Questions
which of the following has three significant digits? a. 305.0 cm b. 1.0008 mm c. 0.0600 m d. 7.060 x 1010
Answers
The correct answer is option A, which is 305.0 cm. A significant digit is any digit that contributes to the precision of a measurement. In this case, the digit 3, 0, and 5 are significant because they indicate the actual measurement.
The decimal point also plays a significant role in determining the number of significant digits. Therefore, in option A, the digit 0 after the decimal point is also significant. Option B has four significant digits because of the digit 8 after the third decimal place. Option C has only two significant digits because the digit 0 before the decimal point is not significant. Option D is written in scientific notation and has four significant digits as well. So, to summarize, option A has three significant digits as it has 305.0, which is a significant measurement with three digits.
To know more about Significant visit:
https://brainly.com/question/2005359
#SPJ11
What is the slope of the line that passes through the points (5, 6) and (5,9)
Answers
Answer:
undefined or no solution
Step-by-step explanation:
it repeats the same x-value
Answer:3
Step-by-step explanation:
9-6
over
6-5
=3/1
simplify
m=3
Suppose that you want to model the height of a rider on a Ferris wheel as a function of time. The amplitude of the function you use as a model should be equal to which of the following
Answers
The amplitude of a periodic function represents the maximum displacement or distance from the mean or equilibrium position.
In the case of modeling the height of a rider on a Ferris wheel as a function of time, the amplitude would represent the maximum height reached by the rider.
Typically, the amplitude of a Ferris wheel model would correspond to the highest point the rider reaches above the ground or the center of the wheel. Therefore, the amplitude of the function used as a model for the height of a rider on a Ferris wheel should be equal to the highest point reached by the rider during the ride.
To know more about function visit:
brainly.com/question/30721594
#SPJ11
How many times must a fair coin be flipped in order to ensure that there is at least a 99% chance of
getting at least one tail?
Answers
What does 100% increase mean???
Answers
Answer:
double whatever you got
100 percent increase of 2 is 4
Step-by-step explanation:
hopes this helps please mark brainliest
Answer:
It means that whatever you have just doubled.
Step-by-step explanation:
If I have a total of 100 widgets, that is 100%. If I have a 100% increase of that value, that means I now have 200 widgets.
What is the slant height of a square pyramid that has a surface area of 319 square feet and a side length of 11 feet?
9 ft
10 ft
11 ft
8 ft
Answers
Answer:
the 319 square feet and side length of 11 feet is 10ft
A cylinder shaped container is used to hold watef . This cylinder has a height of 12 inches and a diameter of 7 inches . A spherical ball with a diameter of 6 inches is dropped into the container . Explain how the ball changes the volhme of the water the container can hold and calculate the amount of water the cylinder can hold after the ball is dropped into the cylinder . Let pi = 3.14
Answers
Answer:
423.9 inches³
Step-by-step explanation:
First we will calculate the volume of the cylinder using the formula
Vc = hπr²
Vc = 12π(3.5)² [radius is 1/2 diameter]
Vc = 147π
Next we calculate the volume of the sphere using 4/3*πr³
Vs = 4/3 πr³
Vs = 4/3π3³
Vs = 12π
Finally, we subtract the volume of the cylinder by the volume of the sphere to get the remaining volume in the cylinder that can be filled with water.
147π - 12π = 135π
Using the approximate 3.14, the answer is 423.9 inches³
3 of 25 After running a coiled tubing unit for 81 minutes, Tom has 9,153 feet of coiled tubing in the well. After running the unit another 10 minutes, he has 10,283 feet of tubing in the well. His call sheet shows he needs a total of 15,728 feet of tubing in the well. How many more feet of coiled tubing does he need to run into the well? feet 4 of 25 Brendan is running coiled tubing in the wellbore at a rate of 99.4 feet a minute. At the end of 8 minutes he has 795.2 feet of coiled tubing inside the wellbore. After 2 more minutes he has run an additional 198.8 feet into the wellbore. How many feet of coiled tubing did Brendan run in the wellbore altogether? 5 of 25 Coiled tubing is being run into a 22,000 foot wellbore at 69.9 feet per minute. It will take a little more than 5 hours to reach the bottom of the well. After the first four hours, how deep, in feet, is the coiled tubing? feet
Answers
3) The extra number of feet of coiled tubing Tom needs to run into the well is: 5445 ft
4) The total length of coiled tubing Brendan ran in the wellbore is: 994 ft
5) The distance that the coiled tubing has reached after the first four hours is: a depth of 16,776 feet in the well.
How to solve Algebra Word Problems?3) Initial amount of coiled tubing he had after 81 minutes = 9,153 feet
Amount of tubing after another 10 minutes = 10,283 feet
The total tubing required = 15,728 feet.
The extra number of feet of coiled tubing Tom needs to run into the well is: Needed tubing length - Current tubing length
15,728 feet - 10,283 feet = 5,445 feet
4) Speed at which Brendan is running coiled tubing = 99.4 feet per minute.
Coiled tubing inside the wellbore after 8 minutes is: 795.2 feet
Coiled tubing inside the wellbore after 2 more minutes is: 198.8 feet
The total length of coiled tubing Brendan ran in the wellbore is:
Total length = Initial length + Additional length
Total length = 795.2 feet + 198.8 feet
Total Length = 994 feet
5) Rate at which coiled tubing is being run into a 22,000-foot wellbore = 69.9 feet per minute. After the first four hours, we need to determine how deep the coiled tubing has reached.
A time of 4 hours is same as 240 minutes
Thus, the distance covered in the first four hours is:
Distance = Rate * Time
Distance = 69.9 feet/minute * 240 minutes
Distance = 16,776 feet
Read more about Algebra Word Problems at: https://brainly.com/question/21405634
#SPJ4
Hi! I hope u can help but I least quickly if possible :D
Answers
How many pint are in 28 cups
Answers
Answer:
14 pints are in 28 cups
Step-by-step explanation:
Answer:
14 pints in 28 cup
Step-by-step explanation:
Find the Laplace transforms of the following functions. 15e⁻ᵗu(t) + sin(t/3)u(t
Answers
The Laplace transform of the given function \(\(15e^{-t}u(t) + \sin\left(\frac{t}{3}\right)u(t)\)\) is \(\(15\left(\frac{1}{s+1}\right)\) + \(\frac{\frac{1}{3}}{s^2 + \left(\frac{1}{3}\right)^2}\)\), where s is the complex variable in the Laplace
To find the Laplace transform of the given function, we will apply the properties and formulas of Laplace transforms. The Laplace transform of \(\(e^{-at}u(t)\) is \(\frac{1}{s+a}\)\), where a is a positive constant. Thus, the Laplace transform of\(\(15e^{-t}u(t)\)\) is\(\(15\left(\frac{1}{s+1}\right\).\)
The Laplace transform of \(\(\sin(bt)\)\) is \(\(\frac{b}{s^2+b^2}\)\), where \(b\) is a constant. Therefore, the Laplace transform of \(\(\sin\left(\frac{t}{3}\right)\)\)
Since the Laplace transform is a linear operation, we can add the individual Laplace transforms of each term in the given function. Thus, the Laplace transform of\(\(15e^{-t}u(t) + \sin\left(\frac{t}{3}\right)u(t)\)\) is \(\(15\left(\frac{1}{s+1}\right) + \frac{\frac{1}{3}}{s^2 + \left(\frac{1}{3}\right)^2}\).\) This is the Laplace transform representation of the given function in the Laplace domain.
Learn more about Laplace here:
https://brainly.com/question/30759963
#SPJ11
suppose that professor degroot has a policy of giving as to the top 10% of student scores on his final, regardless of the actual scores. if the distribution of scores on his final exam turns out to be normal with mean 69 and standard deviation 9, how high does your score have to be to earn an a?
Answers
Your score must be greater than or equal to 81 in order to receive an A grade. The mean value comes out to be 80.52.
Here, we are given that professor Degroot has a policy of giving A grade to the top 10% of student scores on his final.
This means in order to earn an A grade, your score should be in the top 10%.
⇒ Z score should be 0.09
we can look at the z tables to find that this value is at z = 1.28
Now, we know z score is calculated as-
z = (X - μ)/ σ
where X = observed value
μ = sample mean
σ = standard deviation
substituting the given values in the formula we get-
1.28 = (X - 69)/ 9
1.28 × 9 = X - 69
11.52 = X - 69
X = 11.52 + 69
X = 80.52
Thus, your score must be greater than or equal to 81 in order to receive an A grade.
Learn more about z tables here-
https://brainly.com/question/25638875
#SPJ4
I need help With this Math assighnment.
Answers
Answer:
$3.60
Step-by-step explanation:
Hope this helped
General Sherman, a tree located in Sequoia National Park, stands 275
feet tall. To see the top of the tree, Carlos looks up at a 15° angle of elevation. If Carlos is 6 feet tall, how far is he from the base of the tree to the nearest foot? There are 4 options A.1004 B.1020 C.1026 D.1049
Answers
Answer:
Step-by-step explanation:
If Carlos is 6ft tall and looks up at the tree that is 275 ft tall, subtract those two.
275 - 6 = 269
Use tangent with the given angle and the new height. The distance is x.
tan15 = 269/x
x = 269/tan15
x = 1004ft
The distance from Carlos to the tree, given he is 6 feet tall and looks up at a 15° angle of elevation to see the top of a 275-foot tall tree located in Sequoia National Park, is 1026.
Hence option C is correct.
According to the information given,
We can set up a right triangle with Carlos's eye level, the top of the tree, And the base of the tree as the three points of the triangle.
Carlos's height of 6 feet can be used as one side of the triangle,
And we can use the tangent function to find the length of the adjacent side.
A tangent of 15 degrees is equal to the opposite side (height of the tree) divided by the adjacent side (distance from Carlos to the tree).
So, we can solve for the adjacent side by multiplying the height of the tree by the tangent of 15 degrees:
tan(15) = height of the tree / distance from Carlos to the tree
Distance from Carlos to the tree = height of the tree / tan(15)
Plugging in the values given:
Distance from Carlos to the tree = 275 / tan(15)
≈ 1026
Therefore,
The nearest foot to the distance from Carlos to the tree is option C. 1026.
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ2
If the length of the perpendicular from the origin of the line 3x+2y = 6 is m. What is the value of m?
Answers
Answer:
-√13/13 or -2.774
Step-by-step explanation:
(3+2-6/√3²+2²)
$2,300 invested at 7.5% for 10 years. In simple interest
Answers
Answer:
here's the answers............
If $14,000 is invested in an account for 15 years. Calculate the total interest earned at the end of 15years if the interest is:(a) 7% simple interest: $(b) 7% compounded annually: $(c) 7% compounded quarterly: $(d) 7% compounded monthly: $Round your answers to the nearest cent.
Answers
Hello!
Let's solve alternative (a):
For simple interest, we'll use the formula below:
\(A=P(1+\frac{r}{100}\cdot t)\)Let's replace them with the values:
\(\begin{gathered} A=14,000(1+0.07\cdot15) \\ A=14,000(1+1.05) \\ A=14,000\cdot2.05 \\ A=\$28,700 \end{gathered}\)Solving alternative (b):
To compound interest, we'll modify the formula:
\(A=P(1+\frac{r}{100})^t\)So, we'll have:
\(\begin{gathered} A=14,000(1+0.07)^{15} \\ A=14,000(1.07)^{15} \\ A=14,000\cdot2.75903 \\ A=\$\text{ }38,626.42 \end{gathered}\)Solving alternative (c):
\(\begin{gathered} A=P(1+\frac{r}{4})^{4t} \\ A=14,000(1+\frac{0.07}{4})^{4\cdot15} \\ A=14,000(1.0175)^{60} \\ A\cong$ \$\text{ }39,645.43 $ \end{gathered}\)Solving alternative (d):
\(\begin{gathered} A=P(1+\frac{r}{12})^{12\cdot t} \\ A=14,000(1+\frac{0.07}{12})^{12\cdot15} \\ A\cong\$\text{ }$ 39,885.25 $ \end{gathered}\)Think about a moment when you felt stressed. Share how were you able to recognize that you were stressed? ( Can you guys help my math teacher asked us this but i really don't have any stressful moments)
Answers
Answer:
Ok, I'm actually really stressed right now. My crush asked me to the mid-semester dance, but I turned down his twin to go with my friends. I know them both REALLY well, and now I don't know what to do! My besties are pressuring me to say "YES" and I really want to, but it'll break my crush's twin's heart. And again, I know them both REALLY well! STRESSFUL TIMES! :)
Which situation could be represented by the equation-30 + 30=0 ?
Answers
Answer:30x0
Step-by-step explanation:
Karla invested $33,800 in two separate investment accounts. One of the accounts earned 6% annual interest while the other account earned 11% annual interest. If the combined interest earned from both accounts over one year was $2,895.50, how much money was invested in each account? was invested in the account that earned 6% annual interest. was invested in the account that earned 11% annual interest.
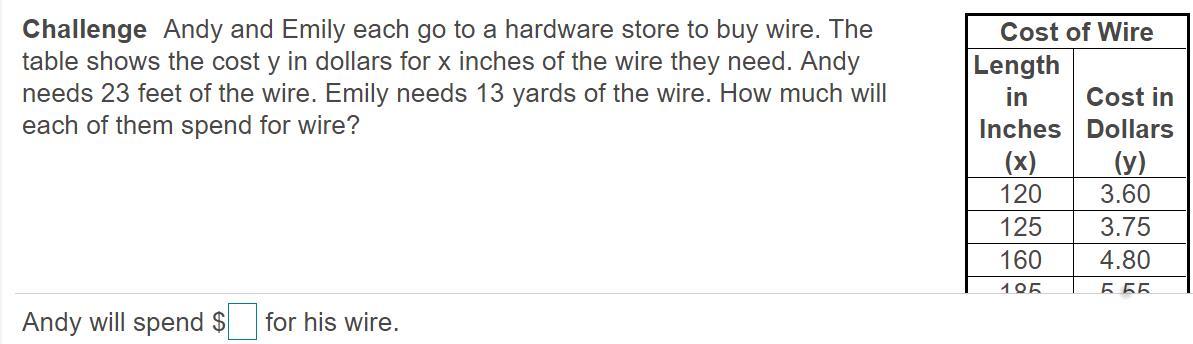
Answers
$15,500 was invested in the account that earned 6% annual interest, while $18,300 was invested in the account that earned 11% annual interest.
Let's assume that the amount invested in the account that earned 6% annual interest is x, and the amount invested in the account that earned 11% annual interest is y. We are given the following information:
x + y = $33,800 (Total amount invested)
0.06x + 0.11y = $2,895.50 (Total interest earned)
We can solve this system of equations to find the values of x and y.
Using the first equation, we can isolate x:
x = $33,800 - y
Substituting this value of x into the second equation, we have:
0.06($33,800 - y) + 0.11y = $2,895.50
Expanding and simplifying the equation, we get:
$2,028 - 0.06y + 0.11y = $2,895.50
Combining like terms, we have:
0.05y = $2,895.50 - $2,028
0.05y = $867.50
Dividing both sides by 0.05, we find:
y = $867.50 / 0.05 = $17,350
Substituting this value of y back into the first equation, we can find x:
x + $17,350 = $33,800
x = $33,800 - $17,350 = $16,450
Therefore, $15,500 was invested in the account that earned 6% annual interest, while $18,300 was invested in the account that earned 11% annual interest.
Learn more about annual interest here:
https://brainly.com/question/14726983
#SPJ11
Given AD = 7x , AB = 3x and the perimeter is 160. Find X.
Answers
Answer:
x = 8
Step-by-step explanation:
The complete question illustrates that the rectangle has sides ABCD and I've represented it as an attachment.
We have that:
AB = 3x
AD = 7x
The perimeter is calculated as:
Perimeter = 2 * (AB + AD)
Substitute values for AB, AD and Perimeter
160 = 2 * (3x + 7x)
160 = 2 * 10x
160 = 20x
Divide both sides by 20
8 = x
x = 8
Answer quickly!!!!!!!!!!!!
Answers
Answer:
a
Step-by-step explanation:
Lin is comparing the graph of two functions g and f. The function g
is given by g(x) = f(x - 2). Lin thinks the graph of g will be the same as
the graph of f, translated to the left by 2. Do you agree with Lin? Explain
your reasoning.
Answers
Lin is correct in thinking that the graph of g will be the same as the graph of f, translated to the left by 2 units.
The function g(x) = f(x - 2) is obtained by shifting the graph of f to the right by 2 units, which means that the point (a, f(a)) on the graph of f is mapped to the point (a - 2, f(a)) on the graph of g. Therefore, the shape of the graph of f remains the same, but its position is shifted to the right by 2 units to obtain the graph of g.
This can be seen by considering the effect of the transformation on the key features of the graph of f, such as its intercepts, maxima, and minima. For example, if f has a maximum at x = c, then g will have a maximum at x = c + 2. Similarly, if f intersects the x-axis at x = d, then g will intersect the x-axis at x = d + 2.
Therefore, Lin's reasoning is correct, and the graph of g will be the same as the graph of f, translated to the left by 2 units.
To learn more about graph click here: brainly.com/question/17267403
#SPJ11
Please help I’ll give brainliest
Answers
Answer:
15
Step-by-step explanation:
15 cubed (15×15×15) equals 3375
Write a polynomial expression that has the following characteristics: The polynomial expression is a trinomial. The polynomial expression has degree 2. The leading coefficient is -5. 6
Answers
Answer:
\( { - 5.6}xy ^{2} + yx + 2x\)
a season pass to the amusement park costs $117, and daily admission costs $39. Determine the number of trips to the park for which paying daily admission is more expensive than purchasing a season pass
Answers
Since we want to find the number of trips to the park for which paying daily admission is more expensive than purchasing a season pass, we can express an inequality, like this:
total daily admission cost > season pass cost
The total daily admission cost, can be expressed as the number of days that this pass is purchased (n) times the daily admission cost ($39), and the season pass cost equlas $117, then we get:
$39*n > $117
From this expression we can solve for n, then we get:
\(\begin{gathered} 39n>117 \\ \frac{39n}{39}>\frac{117}{39} \\ n>3 \end{gathered}\)Then, more than 3 daily passes would be more expensive than the season pass. Since it must be more than 3, the answer is 4 trips
I REALLY NEED HELP QUICK PLEASE!!!
Answers
Answer:
If the correction of 6 * 6X is accurate then I hope this is the answer.
Step-by-step explanation:
6(6x)+3x=3+3x+5
1. First multiply 6 by 6
36x+3x=3+3x+5
2. Then add 36X and 3X
39x=3+3x+5
3. After that add 3 and 5
39x=3x+8
4. Subtract 3x from both sides of the equation.
39x−3x=8
5. Subtract 3x from 39x
36x=8
6. Divide
36X. 8
______. = ______
36. 36
7. 36X and 36 cancel out because they
are common factors
8. The common factor between 8 and 36 is 4.
S you are left with. 2
X= _____
9
_
9. If you would like the decimal, than it is, X = 0.2
I need to know this right now :(
Answers
Answer:
40000
400
Step-by-step explanation:
40000 because 4000 * 10 = 40000
400 because 1 / 10 of 4000 = 400
Answer:
ok so 1/2 is your answer 1/4 divide = 1//2 !
Step-by-step explanation:
What is the slope of the line that passes through the points (10, 4) and
(7, 3)? Write your answer in simplest form.
Answers
================================================
Work Shown:
\((x_1,y_1) = (10,4) \text{ and } (x_2,y_2) = (7,3)\\\\m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}\\\\m = \frac{3 - 4}{7 - 10}\\\\m = \frac{-1}{-3}\\\\m = \frac{1}{3}\\\\\)
-----------------
Extra info:
A slope of 1/3 means "go up 1, then to the right 3"
Think of it like this
slope = rise/run = 1/3
rise = 1 = go up 1
run = 3 = go to the right 3
The circumference of Circle K is $\pi$ . The circumference of Circle L is $4\pi$ . Two circles, one labeled "Circle K" and the other as "Circle L." What is the value of ratio of their circumferences? Of their radii? Of their areas? Write the ratios as fractions in simplest form.
Answers
Answer:
Step-by-step explanation:
Given the circumference of Circle K = π
circumference of Circle L = 4π
Ratio of their circumferences = Ck/Cl
Ratio of their circumferences = π/4π
Ratio of their circumferences = 1/4 = 1:4
For their radii
C = 2πr
for circle k with circumference π
π = 2πrk
1 = 2rk
rk = 1/2
for circle l with circumference 4π
4π = 2πr
4 = 2r
r = 4/2
rl = 2
ratio
rk/rl = 1/2/2
rk/rl = 1/4 = 1:4
for the areas
Area of a circle = πr²
for circle k
Ak = π(1/2)²
Ak = π(1/4)
Ak = π/4
for circle l
Al = π(2)²
Al = 4π
Ratio of their areas
Ak/Al = π/4/(4π)
Ak/Al = π/16π
Ak/Al = 1/16 = 1:16