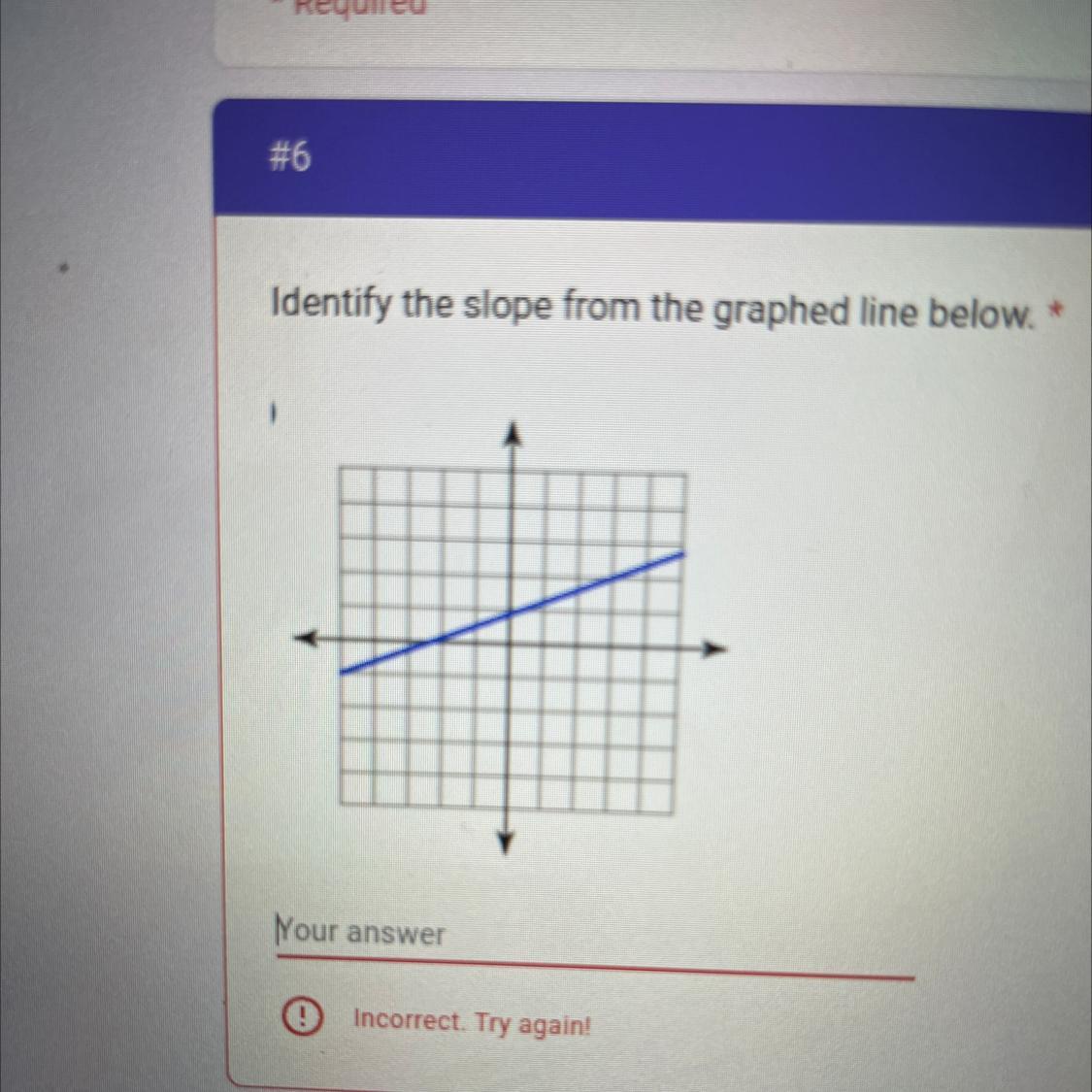
Answers
Answer:
\(m=\frac{1}{3}\)
Step-by-step explanation:
Assuming that the graph is the following:
\((-3,0) (0,1)\)
Use the slope change formula.
\(m=\frac{y{_2}-y_1}{x{_2}-x_1}\)
Substitute and Solve.
\(m=\frac{1-(0)}{0-(-3)}\)
\(m=\frac{1}{3}\)
Related Questions
What is the slope of the equation Y= 5/4 x - 7/4?
a. -7
b. -7/4
c. 5/4
d. 5
Answers
Answer:
a
Step-by-step explanation:
Answer: c
Step-by-step explanation:
solve the equation 2x(2-6)=4(3+1x-2)
Answers
Answer:
no solution
Step-by-step explanation:
if you distribute and simplify:
4x-12 = 12+4x-8
4x-12 = 4x+4
-12 ≠ 4
Answer:
\(x = - \frac{1}{3} \)
Step-by-step explanation:
1) Simplify 2 - 6 to -4.
\(2x \times - 4 = 4(3 + 1 \times x - 2)\)
2) Simplify 1 × x to x.
\(2x \times - 4 = 4(3 + x - 2)\)
3) Simplify 3 + x - 2 to x + 1.
\(2x \times - 4 = 4(x + 1)\)
4) Simplify 2x × -4 to -8x.
\( - 8x = 4(x + 1)\)
5) Divide both sides by 4.
\( - 2x = x + 1\)
6) Subtract x from both sides.
\( - 2x - x = 1\)
7) Simplify -2x - x to -3x.
\( - 3x = 1\)
8) Divide both sides by -3.
\(x = - \frac{1}{3} \)
Therefor, the answer is x = -1/3.
Choose the slope-intercept form of y + 3 = 4(x – 5).
Answers
Answer:
y=4x-23
Step-by-step explanation:
y+3=4(x-5)
y+3=4x-20
y=4x-20-3
y=4x-23
Use polar coordinates to find the volume of the given solid. Below the paraboloid z = 32 − 2x2 − 2y2 and above the xy-plane
Answers
From using the polar coordinates, the volume of a solid present below the paraboloid z = 32 − 2x² − 2y² and above the xy-plane is equals to the 256π.
The polar coordinates of a point is like cartesian coordinates (x,y) describe its position in terms of a distance from a fixed point say origin and an angle measured from a fixed direction, that is (r, θ). The volume of a solid can be determined by using a double integral. The volume of solid is determined by the expression, \(V= \int \int_D f ( r , θ ) r d r d θ\).
We have a paraboloid z = 32 − 2x² − 2y², and determine the volume of solid below the paraboloid and above xy-plane.
Change the cartesian coordinates into polar coordinates, put \(x= rcos(θ)\) , \(y = rsin(\theta)\) and z = 0
=> 32 − 2x² − 2y² = 0
=> 32 = 2( x² + y²)
=> 16 = x² + y² = r² ( since r² cos²θ + r²sin²θ = x² + y²)
=> r² = 16
=> r = ± 4, but r is always positive so, 0≤ r≤ 4 and for angle, 0≤ θ≤ 2π. Also, we can rewrite the paraboloid, z = f(r,θ)= 32 - 2r² in polar coordinates. Using the volume integral, \(V = \int_{0}^{2π} \int_{0}^{4}( 32- 2r²) r d r d θ\)
\(= \int_{0}^{2π} \int_{0}^{4}( 32r - 2r³) d r d θ\)
=\( \int_{0}^{2π} [ \frac{32r^2}{2}- \frac{2r⁴}{4}]_{0}^{4} d θ\)
= \(\int_{0}^{2π} ( \frac{32(4²)}{2}- \frac{2(4)⁴}{4}) d θ\)
\(= \int_{0}^{2π} 16 d θ\)
\(= [128θ]_{0}^{2π} \)
= 256π
Hence, required volume value is 256π.
For more information about polar coordinates, visit:
https://brainly.com/question/29012031
#SPJ4

Refer to the figure: The Triangle
Midsegment Theorem says the midpoints
(K and L) of two sides of a triangle will
result in parallel third sides such that KL is
half of MN.
A. Sketch ∆JKL and ∆JMN separately in the space below. Label all vertices.
Then explain, in detail, how you could
justify that the two triangles are similar, using the results of the Midsegment
Theorem.
What is the scale factor between the two triangles and how do you know?
Answers
Answer:
The Triangle Midsegment Theorem states that, if we connect the midpoints of any two sides of a triangle with a line segment, then that line segment satisfies the following two properties
Step-by-step explanation:
What is the domain of the fuction represented by the table

Answers
Step-by-step explanation:
Domain is the independent variable x. All values listed in x column are in Domain
So, Domain = {5, 10, 15, 20, 25}
NEED ANSWER BY TODAY ( Nov 12, 2020 ) AT 6:30 p.m. ASAP.
The world's future society predicts that by the year 2020, airplanes will be able to carry 1400 passengers. Today's biggest jets carry 600 passengers. What will be the percent of the increase of airplane passengers?
P.S. this is a Percent increase/decrease
from: 600
to: 1400
%/100 = differences of to and from/ from ( before the number )
( no negative difference, bigger number subtract smaller number)
Answers
Answer:
133.33333333 percent
the diffrence is 800
Step-by-step explanation:
[(1400 - 600) / 600] × 100%
= 1.3333333333 × 100%
= 133.33333333%
Answer:
133.33% increase
Step-by-step explanation:
This is a percent increase, and to solve for one you need to know the following formula
\(|\frac{new~value~-~original~value}{original~value}| *100\)
Plugging it in;
New value = 1400
Old value = 600
\(|\frac{new~value~-~original~value}{original~value}|= |\frac{1400-600}{600}| = |\frac{800}{600}| = 1.333333333\)
1.3333333 as a percent is
133.33%
So you have an increase of 133.33%
Suppose each license plate in a certain state has three digits followed by three letters. The digits 4 and 5 are not used. So, there are 26 letters and 8 digits that are used. Assume that the letters and digits can be repeated. How many license plates can be generated using this format?
Answers
The required, there are 8998912 possible license plates that can be generated using this format.
Here, we have,
There are 8 digits that can be used for each of the three digits on the license plate, with two digits (4 and 5) that cannot be used.
Therefore, there are 8 choices for each of the three digits,
giving us 8 x 8 x 8 = 512 possible combinations for the digits.
Similarly, there are 26 letters that can be used for each of the three letters on the license plate.
Therefore, there are 26 choices for each of the three letters, giving us 26 x 26 x 26 = 17576 possible combinations for the letters.
Total number of license plates = number of choices for the digits x number of choices for the letters
= 512 x 17576
= 8998912
Therefore, there are 8998912 possible license plates that can be generated using this format.
Learn more about combination here:
brainly.com/question/13387529
#SPJ1
the unit circle is the circle centered at with radius
Answers
The unit circle is the circle centered at with radius The unit circle is a circle centered at the origin with a radius of 1 unit. It plays a fundamental role in trigonometry, providing a geometric representation of the trigonometric functions
The unit circle is a circle that is centered at the origin (0, 0) of a coordinate plane and has a radius of 1 unit. In other words, it is a circle with a diameter of 2 units.
The unit circle is particularly significant in mathematics, especially in trigonometry. Its properties and relationships with angles are extensively used in various mathematical applications.
One of the main reasons the unit circle is so important is due to its connection with the trigonometric functions sine and cosine. As an angle rotates around the origin,
the coordinates of the point on the unit circle where the terminal side of the angle intersects the circle correspond to the values of sine and cosine of that angle.
For example, if an angle of 30 degrees is measured counterclockwise from the positive x-axis, the coordinates of the corresponding point on the unit circle would be (√3/2, 1/2), which are the values of sine and cosine for that angle.
Additionally, the unit circle provides a convenient way to visualize and understand other trigonometric functions such as tangent, cotangent, secant, and cosecant.
By examining the ratios of the coordinates on the unit circle, we can relate these trigonometric functions to the lengths and angles associated with right triangles.
In summary, the unit circle is a circle centered at the origin with a radius of 1 unit. It plays a fundamental role in trigonometry, providing a geometric representation of the trigonometric functions and aiding in the understanding of angles, ratios, and relationships within the field of mathematics.
To know more about trigonometry refer here:
https://brainly.com/question/11016599#
#SPJ11
Help plz i will mark brilliant

Answers
Answer:
a=100 b=50 c=30
Step-by-step explanation:
30+50+a= 180, A= 100.
90+40+b=180, B=50
A+B+C= 180
100+50+c=180, C=30
i dont know how to do this stuff
im choosing brainliest

Answers
Answer:
5 - 15 = -10
Step-by-step explanation:
Answer:
5 - 15 = -10
Step-by-step explanation:
If you start with 5 and then subtract 15, you end up at -10.
Polina has some juice pouches that each contain 7 fluid ounces of juice. write an equation that relates the number of juice pouches (p) to the total volume of juice (j) in fluid ounces
Answers
Each of Polina's juice pouches holds 7 fluid ounces of juice. A equation that connects the quantity of juice in each pouch to the overall amount in fluid ounces is p-7j=0.
Given that,
Each of Polina's juice pouches holds 7 fluid ounces of juice.
We have to create a equation that connects the quantity of juice in each pouch (p) to the overall amount (j) in fluid ounces.
The equation is p=7j
p-7j=0
Therefore, a equation that connects the quantity of juice in each pouch (p) to the overall amount (j) in fluid ounces is p-7j=0.
To learn more about equation visit: https://brainly.com/question/10413253
#SPJ1
Solve 2k-3(4-k)=3k+4.
Answers
Answer: what he said^
Step-by-step explanation: i like the points
Complete the square
x
2
+
8
x
+
6
Answers
Answer:
2
+
8
+
6Step-by-step explanation:
Answer:
(x + 4)² - 10Step-by-step explanation:
\(x^2+8x+6 =\\\\=\underline{x^2+2\cdot x\cdot 4+4^2}-4^2+6=\\\\=(x+4)^2-16+6=\\\\=(x+4)^2-10\)
what type of region must we have if all six bounds (limits of integration) are constant (numerical values, no variables) in cylindrical coordinates? what about in spherical coordinates? is it possible to have a region represented with only constants in both cylindrical and spherical simultaneously (i.e., the same exact region that can be all constants with both systems)?
Answers
If all six bounds (limits of integration) are constant (numerical values, no variables) in cylindrical coordinates, then we must have a rectangular box-like region.
This is because in cylindrical coordinates, we have three variables: radius, angle, and height. When all six bounds are constants, we are essentially fixing the range of each variable, resulting in a rectangular box-like region.
In spherical coordinates, if all six bounds are constant, then we must have a rectangular pyramid-like region. This is because in spherical coordinates, we have three variables: radius, polar angle, and azimuthal angle. When all six bounds are constants, we are essentially fixing the range of each variable, resulting in a rectangular pyramid-like region.
It is not possible to have the exact same region represented with only constants in both cylindrical and spherical coordinates simultaneously. This is because the two coordinate systems have different geometric shapes and different ways of representing the variables. However, it is possible for the regions to have similar shapes and for the bounds to have similar numerical values in both systems.
For more about cylindrical coordinates:
https://brainly.com/question/31046653
#SPJ11
what equation has the same solution as x^2-16x+20=-2
Answers
The equation that has the same solution as x² - 16x + 20 = -2 is x² - 16x + 22 = 0.
How did we arrive at this assertion?To find an equation with the same solution as the equation x² - 16x + 20 = -2, manipulate the given equation while preserving its solutions.
Starting with the given equation:
x² - 16x + 20 = -2
Move the constant term (-2) to the other side:
x² - 16x + 20 + 2 = 0
Simplifying:
x^2 - 16x + 22 = 0
Therefore, the equation that has the same solution as x² - 16x + 20 = -2 is x² - 16x + 22 = 0.
learn more about equation: https://brainly.com/question/22688504
#SPJ1
Evaluate 11.5x + 10.9y when x = 6 and y =7
Answers
The value of the algebraic expression 11.5x + 10.9y at x = 6 and y = 7 is 145.3
What is an algebraic expression?
Algebraic expression consists of variables and numbers connected with addition, subtraction, multiplication and division
The given algebraic expression is 11.5x + 10.9y
We have to find the value of the algebraic expression at x = 6 and y = 7
Putting x = 6 and y = 7 in the algebraic expression,
\(11.5 \times 6 + 10.9 \times 7\)
69 + 76.3
145.3
To learn more about algebraic expression, refer to the link-
https://brainly.com/question/2164351
#SPJ1
Which expression is equivalent to -2x + 5 ?
10 - 4x - 5 + 2x
3(2x + 1) - x - 1
3x + 5 - x - 10
–x - 9 + 4x + 4
Answers
Step-by-step explanation:
the first one
10 - 4x - 5 + 2x
-4x + 2x = -2x
10 - 5 = 5
so, in sum,
-2x + 5
Which of the following is the factor of 5x - 35?
A. 5(x - 7 ) B. 5(x + 7)
C. 7(x - 5) D. 7(x + 5)
Answers
Answer:
a
Step-by-step explanation:
(3.862 x 15600) - 5.98 is properly written as:
Answers
Answer:
60241.22
Step-by-step explanation:
y=3x +5
y=x+3
Graph the system. Then write its solution. Note that you can also answer "No solution" or "Infinitely many" solutions.
Answers
1.) Given f(x) = x² + 5, which of the following could represent f¹(x)?
f¹(x) = √√x + 5
WORK:
a.
c. f¹(x)=√x - 5
C.
b. f¹(x)=√x + 5
d. f¹(x)=√x - 5
Answers
Nora knit a total of 10 centimeters of scarf over 5 nights. After 6 nights of knitting, how many centimeters of scarf will Nora have knit in total? Solve using unit rates.
Answers
Answer:
Step-by-step explanation:
10 ÷ 5 = 2 x6 = 12
Answer:20
Step-by-step explanation:the answer is 20
trust
= Exercise 1. Let G be a group. Suppose that there exists g € G and a, b e Z such that gº = gø= = e. Prove that gecd(a,b) = e. (Recall that ged(0,0) = 0.)
Answers
This proof shows that if there exists an element g in a group G such that g^n = g^m = e, then g^gcd(n, m) = e.
Let's prove that if there exists an element g in a group G such that g^n = g^m = e, where n and m are integers, then g^gcd(n, m) = e.
First, note that since g^n = e, we have (g^n)^k = e^k = e for any integer k. Similarly, (g^m)^k = e for any integer k.
Now, let d = gcd(n, m). By definition, d divides both n and m, so we can write n = dx and m = dy, where x and y are integers.
Using this, we can express g^n and g^m as (g^d)^x and (g^d)^y, respectively.
Now, consider the exponent k = gcd(x, y). Since k divides both x and y, we can write x = kz and y = kw, where z and w are integers.
Using these expressions, we have (g^d)^x = (g^d)^(kz) and (g^d)^y = (g^d)^(kw).
Using the property mentioned earlier, we know that (g^d)^k = e for any integer k.
Substituting the above expressions, we have (g^d)^x = e^z = e and (g^d)^y = e^w = e.
Therefore, g^gcd(n, m) = g^d = e, as desired.
This proof shows that if there exists an element g in a group G such that g^n = g^m = e, then g^gcd(n, m) = e.
Know more about Property here:
https://brainly.com/question/29134417
#SPJ11
The PTO is selling raffle tickets to raise money for classroom supplies. A raffle ticket costs $4. There is 1 winning ticket out of the 110 tickets sold. The winner gets a prize worth $82. Round your answers to the nearest cent.
What is the expected value (to you) of one raffle ticket? $
Calculate the expected value (to you) if you purchase 10 raffle tickets. $
What is the expected value (to the PTO) of one raffle ticket? $
If the PTO sells all 110 raffle tickets, how much money can they expect to raise for the classroom supplies? $
Answers
The z-score for P(? ≤ z ≤ ?) = 0.60 is approximately 0.25.
The z-score for P(z ≥ ?) = 0.30 is approximately -0.52.
How to find the Z score
P(Z ≤ z) = 0.60
We can use a standard normal distribution table or a calculator to find that the z-score corresponding to a cumulative probability of 0.60 is approximately 0.25.
Therefore, the z-score for P(? ≤ z ≤ ?) = 0.60 is approximately 0.25.
For the second question:
We want to find the z-score such that the area under the standard normal distribution curve to the right of z is 0.30. In other words:
P(Z ≥ z) = 0.30
Using a standard normal distribution table or calculator, we can find that the z-score corresponding to a cumulative probability of 0.30 is approximately -0.52 (since we want the area to the right of z, we take the negative of the z-score).
Therefore, the z-score for P(z ≥ ?) = 0.30 is approximately -0.52.
Read more on Z score here: brainly.com/question/25638875
#SPJ1
9x2 – 12x + 4 = 4
How do I solve by using square root property?
Answers
how do I solve by square root property don't know by if multiply and add you will get the answer it is 10
when the film is placed into the xcp holder with the smooth side of the film towards the throat, after processing it will appear dark. t/f
Answers
The given statement " When the film is placed into the XCP (extension cone paralleling) holder with the smooth side of the film towards the throat, after processing, it will appear darker" is false because it will lighter, not darker.
The smooth side of the film is the side that interacts with the X-ray radiation and receives the image, while the emulsion side contains the light-sensitive crystals that react to the radiation.
Placing the smooth side towards the throat ensures that the image is sharp and clear, as the X-ray beam travels through the teeth and soft tissues before reaching the film.
After processing, the exposed areas of the film turn dark, representing the captured X-ray image, while the unexposed areas remain light or clear.
Know more about X-ray image here:
https://brainly.com/question/29127698
#SPJ11
Select the expression that is equivalent to x + x + y × y × y. Question options: 2x + 3y x2 + 3y x2 + y3 2x + y3
Answers
Answer:
D) 2x + y³---------------------
Adding same values results in multiplication.
Multiplication of same values results in exponents.
Find the equivalent expression with the given:
x + x + y × y × y = 2x + y³This is same as the last answer choice.
Please help me….please

Answers
Answer:
Step-by-step explanation:

what is the area of a circle with a diameter of 15.8 cm? use 3.14 for pi and round your final answer to the nearest hundredth. enter your answer in the box.
Answers
Answer:
196.1 cm^2
Step-by-step explanation:
The area of a circle is given by Area = πr^2
R is (15.8 cm)/2 = 7.9 cm
Area = (3.14)*(7.0cm)^2
Area = 196.1 cm^2
Answer:
The formula to calculate the area of a circle is given by: A = π * r^2, where r is the radius of the circle.
Given the diameter of 15.8 cm, we can calculate the radius by dividing the diameter by 2: r = 15.8 cm / 2 = 7.9 cm
Plugging the value of the radius into the formula: A = π * 7.9^2 = 3.14 * 62.41 = 196.0794 cm^2
Rounding the answer to the nearest hundredth, the area of the circle with a diameter of 15.8 cm is approximately 196.08 cm^2.